Анықталған интегралдарды сандық әдістермен шешу: теория және практикалық қолданылуы


Кіріспе
Қазір ғылыми-техникалық есептердің көбінің ойдағыдай шешілуі көп жағдайда электрондық есептеу машиналарын жедел қолдана білуден тәуелді. Осы мақсатқа жету үшін күшті және ыңғайлы, үлкен және шағын әмбебап, дербес компьютерлер ғана емес, жақсы өңделген сәйкес сандық әдістер және олардың программалық алгоритмдері де қажет.
Қазіргі заман талабына сай есептеуіш техника программалау тілінде үлкен көлемді жұмыстарды орындауға мүмкіндік береді. Осының арқасында әр түрлі математикалық есептеулерді шешуде үлкен жетістіктерге жетуге мүмкіндіктер туды.
Дипломдық жұмыста анықталған интегралды шешудің сандық әдістері қарасатырылған.
Дипломдық жұмыстың екінші тарауында анықталған интегралды сандық шешудің әдістеріне зертханалық тапсырмалар және оларды шешу мысалдары қарастырылған. Мысалдар бойынша алынған нәтижелер мен программаны орындау барысында алынған тестілік (тексеруші) нәтижелер арасында салыстырулар жүргізілген.
1. ИНТЕГРАЛДЫ ЕСЕПТЕУДІҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ
1. 1 Анықталмаған интеграл
1. Тікелей интегралдау. Айнымалыларды алмастыру және
бөлшектеп интегралдау.
Егер
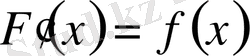 немесе
немесе
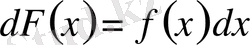 болса, онда
болса, онда
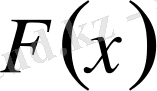 функциясы
функциясы
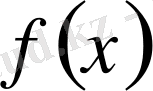 функциясы үшін алғашқы функция деп аталады.
функциясы үшін алғашқы функция деп аталады.
Егер
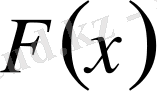 функциясы
функциясы
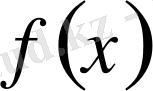 функциясының алғашқы функциясы болса, онда шексіз көп алғашқы функциялары болады. Сонымен бірге, барлық алғашқы функциялар
функциясының алғашқы функциясы болса, онда шексіз көп алғашқы функциялары болады. Сонымен бірге, барлық алғашқы функциялар
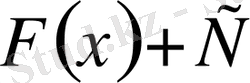 (
(
 - тұрақты сан) өрнегіне кіреді.
- тұрақты сан) өрнегіне кіреді.
Анықтама.
Барлық алғашқы функциялардың жиынтығы
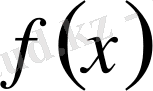 функциясынан (немесе
функциясынан (немесе
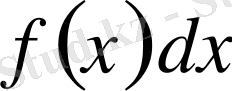 өрнегінен) алынған
анықталмаған интеграл
деп аталады. Ол былай белгіленеді:
өрнегінен) алынған
анықталмаған интеграл
деп аталады. Ол былай белгіленеді:
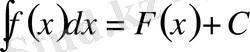 .
.
Мұндағы
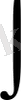 - интеграл белгісі,
- интеграл белгісі,
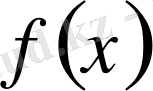 - интеграл астындағы функция,
- интеграл астындағы функция,
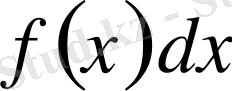 - интеграл астындағы өрнек,
- интеграл астындағы өрнек,
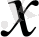 -интегралдау айнымалысы.
-интегралдау айнымалысы.
Анықталмаған интегалды іздеу процесі функцияны интералдау деп аталады.
Анықталмаған интералдың қасиеттері (интегралдау ережелері) .
1)
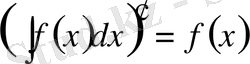 .
.
2)
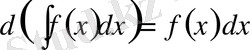 .
.
3)
 .
.
4)
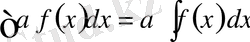 , мұнда
, мұнда
 -тұрақты сан.
-тұрақты сан.
5)
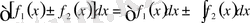 .
.
6) Егер
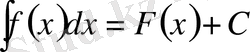 және
және
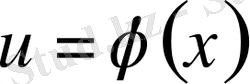 болса, онда
болса, онда
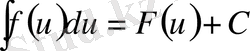 болады.
болады.
Негізгі интегралдардың кестесі
1.
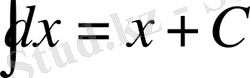 . 9.
. 9.
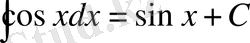 .
.
2.
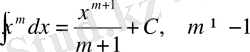 . 10.
. 10.
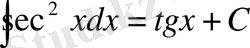
3.
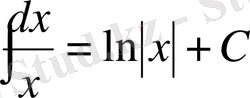 . 11.
. 11.
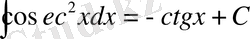 .
.
4.
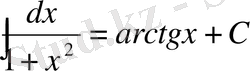 . 12.
. 12.
 .
.
5.
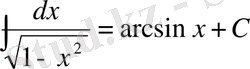 13.
13.
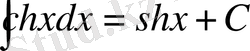 .
.
6.
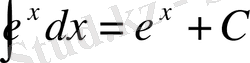 . 14.
. 14.
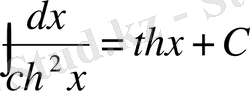 .
.
7.
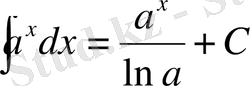 . 15.
. 15.
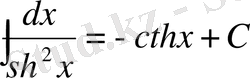
8.
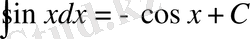 .
.
Анықталмаған интегралда айнымалыларды алмастыру
Анықталмаған интегралда айнымалыларды алмастыру екі түрлі болады:
1)
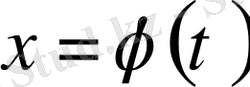 , мұнда
, мұнда
 -
-
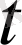 айнымалысына тәуелді монотонды, үзіліссіз дифференциалданатын жаңа функция. Бұл жағдайда айнымалыларды алмастыру формуласы мынадай болады:
айнымалысына тәуелді монотонды, үзіліссіз дифференциалданатын жаңа функция. Бұл жағдайда айнымалыларды алмастыру формуласы мынадай болады:
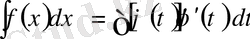 ;
;
2)
 , мұнда
, мұнда
 - жаңа айнымалы. Бұл жағдайда айнымалыларды алмастыру формуласы мынадай болады:
- жаңа айнымалы. Бұл жағдайда айнымалыларды алмастыру формуласы мынадай болады:
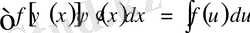 .
.
Негізгі интегралдардың кестесін келесі формулалармен
толықтырайық:
16.
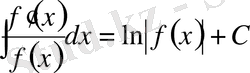 .
.
17.
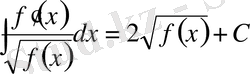 .
.
18.
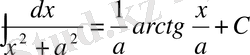 .
.
19.
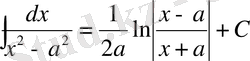 .
.
20.
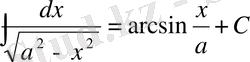 .
.
21.
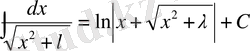 .
.
22.
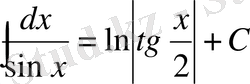 .
.
23.
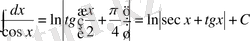 .
.
24.
 . 25.
. 25.
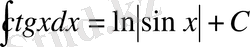 .
.
Бөлшектеп интегралдау .
Функцияны бөлшектеп интегралдау келесі формула арқылы жүргізіледі:
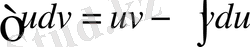 ,
,
мұнда
 ,
,
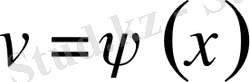 -үзіліссіз интегралданатн
-үзіліссіз интегралданатн
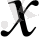 -тен тәуелді функциялар. Бұл формуланың көмегімен
-тен тәуелді функциялар. Бұл формуланың көмегімен
 интегралын табу басқа бір
интегралын табу басқа бір
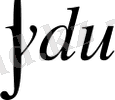 интегралды іздеуге әкеліп соғады.
интегралды іздеуге әкеліп соғады.
Мұнда
 ретінде дифференциалдау кезінде жеңілдейтін функция алынады, ал
ретінде дифференциалдау кезінде жеңілдейтін функция алынады, ал
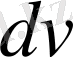 ретінде интеграл астындағы өрнектің интегралы белгілі немесе оңай табылатын бөлігі алынады.
ретінде интеграл астындағы өрнектің интегралы белгілі немесе оңай табылатын бөлігі алынады.
Мысалы,
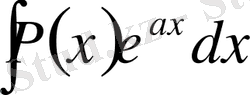 ,
,
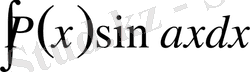 ,
,
 , мұнда
, мұнда
 -көпмүшелік түрінде берілген интегралдар үшін
-көпмүшелік түрінде берілген интегралдар үшін
 ретінде
ретінде
 -ті,
-ті,
 ретінде сәйкесінше
ретінде сәйкесінше
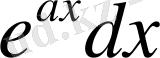 ,
,
 ,
,
 өрнектерін алған дұрыс болады.
өрнектерін алған дұрыс болады.
 ,
,
 ,
,
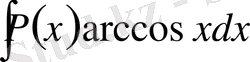 түріндегі интегралдар үшін
түріндегі интегралдар үшін
 ретінде сәйкесінше
ретінде сәйкесінше
 ,
,
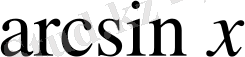 ,
,
 функцияларын, ал
функцияларын, ал
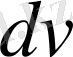 ретінде
ретінде
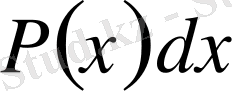 өрнегін алған ыңғайлы болады.
өрнегін алған ыңғайлы болады.
2. Рационал бөлшектерді интегралдау.
Анықтама.
 , мұнда
, мұнда
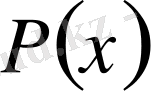 ,
,
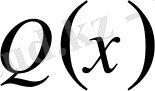 -көпмүшеліктер, түріндегі бөлшек
рационал бөлшек
деп аталады.
-көпмүшеліктер, түріндегі бөлшек
рационал бөлшек
деп аталады.
Егер
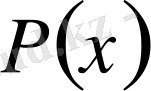 көпмүшелігінің дәрежесі
көпмүшелігінің дәрежесі
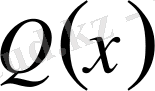 көпмүшелігінің дәрежесінен төмен болса, онда рационал бөлшек дұрыс деп аталады, ал кері жағдайда бұрыс бөлшек деп аталады.
көпмүшелігінің дәрежесінен төмен болса, онда рационал бөлшек дұрыс деп аталады, ал кері жағдайда бұрыс бөлшек деп аталады.
Ең қарапайым (элементар) бөлшектер деп келесі түрдегі дұрыс бөлшектер айтылады:
1.
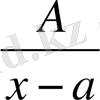 ;
;
2.
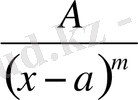 , мұнда
, мұнда
 - 1-ден үлкен бүтін сан.
- 1-ден үлкен бүтін сан.
3.
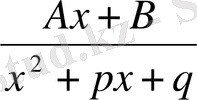 , мұнда
, мұнда
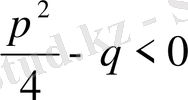 , яғни
, яғни
 квадрат үшмүшелігінің нақты түбірлері жоқ.
квадрат үшмүшелігінің нақты түбірлері жоқ.
4.
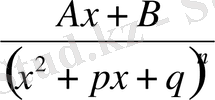 , мұнда
, мұнда
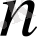 - 1-ден үлкен бүтін сан және
- 1-ден үлкен бүтін сан және
 квадрат үшмүшелігінің нақты түбірлері жоқ.
квадрат үшмүшелігінің нақты түбірлері жоқ.
Барлық төрт жағдайда
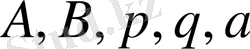 - нақты сандар деп жорамалдаймыз.
- нақты сандар деп жорамалдаймыз.
Бұл қарапайым бөлшектердің алғашқы үш түрінен алынған интегралдарды қарастырайық:
1.
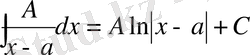 ;
;
2.
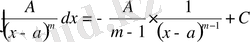 ;
;
3.
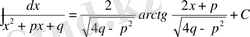 .
.
Шынында,
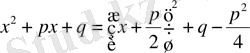 немесе
немесе
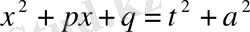 ,
,
мұнда
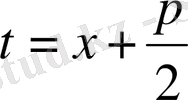 ,
,
 , осыдан
, осыдан
 .
.
Рационал бөлшектерді қарапайым бөлшектерге жіктеу арқылы
интегралдау.
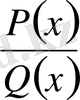 рационал бөлшекті интнгралдамас бұрын келесі алгебралық түрлентірулер мен есептеулер жүргізу керек:
рационал бөлшекті интнгралдамас бұрын келесі алгебралық түрлентірулер мен есептеулер жүргізу керек:
- Егер бұрыс рационал бөлшек берілсе, онда оның сол жағын бөліп алу керек, яғни келесі тгге келтіру керек:
,
мұнда
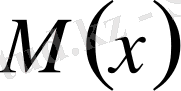 -көпмүшелік, ал
-көпмүшелік, ал
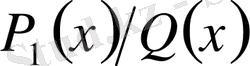 -дұрыс рационал бөлшек;
-дұрыс рационал бөлшек;
2) бөлшектің бөлімін сызықтық және квадраттық көпмүшеліктерге жіктеу керек:
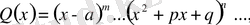
мұнда
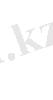
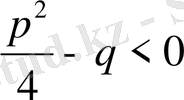 , яғни
, яғни
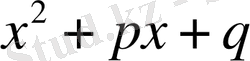 үшмүшелігінің комплексті түйіндес түбірлері бар.
үшмүшелігінің комплексті түйіндес түбірлері бар.
3) дұрыс рационал бөлшекті қарапайым бөлшектерге жіктеу керек:

4)
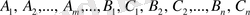 анықталмаған коэффициенттерін есептеу керек. Ол үшін соңғы теңдікті ортақ бөлімге келтіріп, алынған теңтіктің оң және сол жағындағы
анықталмаған коэффициенттерін есептеу керек. Ол үшін соңғы теңдікті ортақ бөлімге келтіріп, алынған теңтіктің оң және сол жағындағы
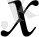 -тің бірдей дәрежесінің алдындағы коэффициенттерді теңестіріп, одан кейін сызықтық теңдеулер системасын шешу керек.
-тің бірдей дәрежесінің алдындағы коэффициенттерді теңестіріп, одан кейін сызықтық теңдеулер системасын шешу керек.
 ,
мұнда
,
мұнда
 -рационал функция, түріндегі интеграл
.
-рационал функция, түріндегі интеграл
.
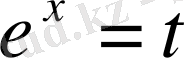 алмастыруының көмегімен көрсетілген түрдегі интеграл рационал ыункциядан алынатын интегралға келтіріледі,
алмастыруының көмегімен көрсетілген түрдегі интеграл рационал ыункциядан алынатын интегралға келтіріледі,
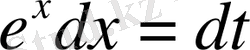 ,
,
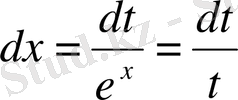 .
.
3. Қарапайым иррационал функцияларды интегралдау.
1)
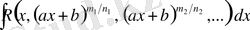 ,
,
 -
рационал функция,
-
рационал функция,
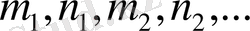 -бүтін сандар, түріндегі интегралдар.
-бүтін сандар, түріндегі интегралдар.
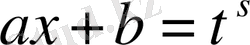 ,
мұнда
,
мұнда
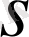 -
-
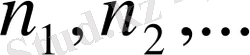 -
сандарының ең кіші ортақ бөлімі, алмастыруының көмегімен берілген интеграл рационал функциядан алынатын интегралға айналады.
-
сандарының ең кіші ортақ бөлімі, алмастыруының көмегімен берілген интеграл рационал функциядан алынатын интегралға айналады.
2)
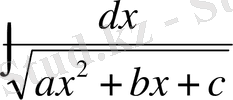 түріндегі интегралдар. Мұндай интегралдар квадрат үшмүшеліктен толық квадратты бөліп алу арқылы 20 немесе 21-ші кестелік интегралдарға келтіріледі.
түріндегі интегралдар. Мұндай интегралдар квадрат үшмүшеліктен толық квадратты бөліп алу арқылы 20 немесе 21-ші кестелік интегралдарға келтіріледі.
3)
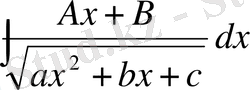 түріндегі интегралдар. Бұл интегралды табу үшін бөлшектің алымына бөлшектің бөлімінде түбір астында тұрған үшмүшеліктің туындысын есептеп жазамыз, одан кейін интегралды екі интегралдың қосындысына жіктейміз:
түріндегі интегралдар. Бұл интегралды табу үшін бөлшектің алымына бөлшектің бөлімінде түбір астында тұрған үшмүшеліктің туындысын есептеп жазамыз, одан кейін интегралды екі интегралдың қосындысына жіктейміз:

4)
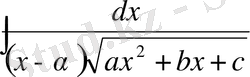 түріндегі интегралдар.
түріндегі интегралдар.
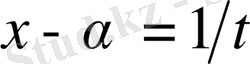 алмастыуын жасағаннан кейін интеграл 9. 2 пункте қарастырылған интегралға келтірідеді.
алмастыуын жасағаннан кейін интеграл 9. 2 пункте қарастырылған интегралға келтірідеді.
5)
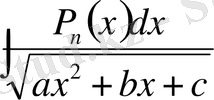 , мұндағы
, мұндағы
 -
-
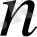 -ші дәрежелі көпмүшелік, түріндегі интегралдар. түріндегі интегралдар. Мұндай интегралдар келесі теңдіктің көмегімен табылады:
-ші дәрежелі көпмүшелік, түріндегі интегралдар. түріндегі интегралдар. Мұндай интегралдар келесі теңдіктің көмегімен табылады:
 ,
,
мұнда
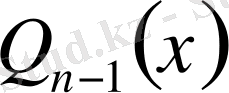 -коэффициенттері анықталмаған
-коэффициенттері анықталмаған
 -ші дәрежелі көпмүшелік,
-ші дәрежелі көпмүшелік,
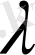 -сан.
-сан.
Көрсетілген теңдікті дифференциалдап, нәтижесін ортақ бөлімге келтіріп екі көпмүшеліктен тұратын теңдік аламыз. Одан
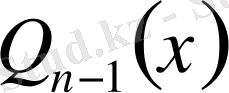 көпмүшелігінің коэффициенттері мен
көпмүшелігінің коэффициенттері мен
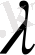 санын анықтауға болады.
санын анықтауға болады.
6) Дифференциалдық биномдардан алынған интеграл
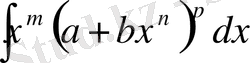 , мұнда
, мұнда
 -рационал сандар.
-рационал сандар.
П. Л. Чебышев дәлелдегендей, дифференциалдық биномдардан алынатын интеграл тек қана келесі үш жағдайда ғана элементар функциялар арқылы өрнектеледі:
1)
 -бүтін сан, онда берілген интеграл
-бүтін сан, онда берілген интеграл
 алмастыруының көмегімен рационал функциядан алынатын интегралға келтіріледі,
алмастыруының көмегімен рационал функциядан алынатын интегралға келтіріледі,
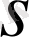 -
-
 мен
мен
 -нің ең кіші ортақ еселігі. .
-нің ең кіші ортақ еселігі. .
2)
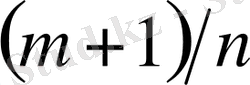 -бүтін сан, бұл жағдайда берілген интеграл
-бүтін сан, бұл жағдайда берілген интеграл
 алмастыруының көмегімен рационал функциядан алынатын интегралға келтіріледі.
алмастыруының көмегімен рационал функциядан алынатын интегралға келтіріледі.
3)
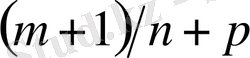 -бүтін сан, бұл жағдайда берілген интеграл
-бүтін сан, бұл жағдайда берілген интеграл
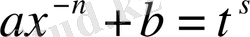 , мұнда
, мұнда
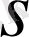 -
-
 бөлшегінің бөлімі, алмастыруының көмегімен рационал функциядан алынатын интегралға келтіріледі.
бөлшегінің бөлімі, алмастыруының көмегімен рационал функциядан алынатын интегралға келтіріледі.
4. Тригонометриялық функцияларды интегралдау
1)
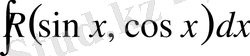 , мұнда
, мұнда
 -рационал функция, түріндегі интегралдар. Бұл түрдегі интегралдар жан-жақты деп аталатын
-рационал функция, түріндегі интегралдар. Бұл түрдегі интегралдар жан-жақты деп аталатын
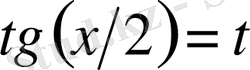 тригонометриялық алмастыруының көмегімен рационал функциядан алынатын интегралға келтіріледі. Нәтижесінде алатынымыз:
тригонометриялық алмастыруының көмегімен рационал функциядан алынатын интегралға келтіріледі. Нәтижесінде алатынымыз:
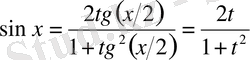 ;
;
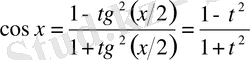 ;
;
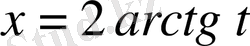 ;
;
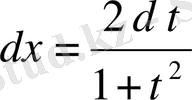 .
.
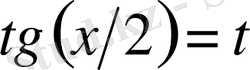 жан-жақты алмастыруы көп жағдайларда күрделі есептеулерге әкеліп соғады, себебі оны қолданғанда
жан-жақты алмастыруы көп жағдайларда күрделі есептеулерге әкеліп соғады, себебі оны қолданғанда
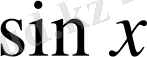 пен
пен
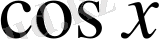
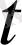 арқылы
арқылы
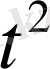 кіретін рационал бөлшектер түрінде өрнектеледі. Кейбір дербес жағдайларда
кіретін рационал бөлшектер түрінде өрнектеледі. Кейбір дербес жағдайларда
 түріндегі иншгралдарды есептеу жеңілдетіледі.
түріндегі иншгралдарды есептеу жеңілдетіледі.
1. Егер
 -
-
 -ке қатысты тақ функция болса, яғни
-ке қатысты тақ функция болса, яғни
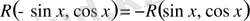 болса, онда
болса, онда
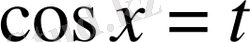 алмастыруын жасау арқылы берілген интеграл рационал функциядан алынатын интегралға келтіріледі.
алмастыруын жасау арқылы берілген интеграл рационал функциядан алынатын интегралға келтіріледі.
2. Егер
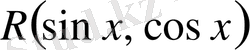 -
-
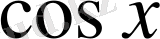 -ке қатысты тақ функция болса, яғни
-ке қатысты тақ функция болса, яғни
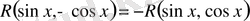 болса, онда
болса, онда
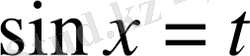 алмастыруын жасау арқылы берілген интеграл рационал функциядан алынатын интегралға келтіріледі.
алмастыруын жасау арқылы берілген интеграл рационал функциядан алынатын интегралға келтіріледі.
3. Егер
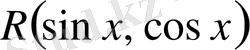 -
-
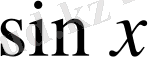 және
және
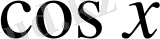 -ке қатысты жұпфункция болса, яғни
-ке қатысты жұпфункция болса, яғни
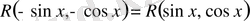 болса, онда
болса, онда
 алмастыруын жасау арқылы берілген интеграл рационал функциядан алынатын интегралға келтіріледі.
алмастыруын жасау арқылы берілген интеграл рационал функциядан алынатын интегралға келтіріледі.
2)
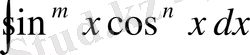 түріндегі интегралдар. Мұнда маңызды болып саналатын екі жағдайды қарастырамыз.
түріндегі интегралдар. Мұнда маңызды болып саналатын екі жағдайды қарастырамыз.
1-жағдай.
 және
және
 көрсеткіштерінің ең болмағанда біреуі оң тақ сан. Егер
көрсеткіштерінің ең болмағанда біреуі оң тақ сан. Егер
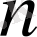 - оң тақ сан болса, онда
- оң тақ сан болса, онда
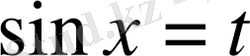 алмастыруы қолданылады, ал егер
алмастыруы қолданылады, ал егер
 оң тақ сан болса, онда
оң тақ сан болса, онда
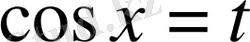 алмастыруы қолданылады.
алмастыруы қолданылады.
2-жағдай
.
 және
және
 көрсеткіштерінің екеуі де оң жұп сандар болса, онда интеграл астындағы функцияны келесі формулалардың көмегімен түрлендіру керек:
көрсеткіштерінің екеуі де оң жұп сандар болса, онда интеграл астындағы функцияны келесі формулалардың көмегімен түрлендіру керек:
 ,
,
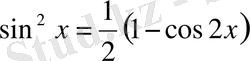 ,
,
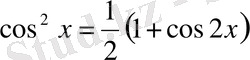 .
.
3)
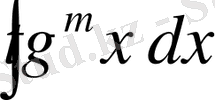 және
және
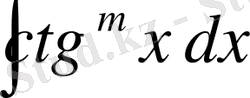 түріндегі интегралдар,
түріндегі интегралдар,
 -оң бүтін сан. Мұндай мнтегралдарды іздеген кезде
-оң бүтін сан. Мұндай мнтегралдарды іздеген кезде
 (немесе
(немесе
 ) формулалары қолданылады. Оның көмегімен тангенс пен котангенстің дәрежелері біртіндеп төмендетіледі.
) формулалары қолданылады. Оның көмегімен тангенс пен котангенстің дәрежелері біртіндеп төмендетіледі.
4)
 және
және
 түріндегі интегралдар,
түріндегі интегралдар,
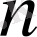 -оң жұпсан. Мұндай интегралдар 3 пункте көрсетілген интегралдар сияқты
-оң жұпсан. Мұндай интегралдар 3 пункте көрсетілген интегралдар сияқты
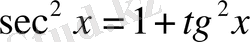 (немесе
(немесе
 ) формулаларынң көмегімен есептеледі.
) формулаларынң көмегімен есептеледі.
5)
 және
және
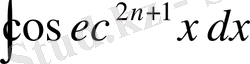 түріндегі интегралдар. Мұнда келесі рекурентті формулаларды пайдалану керек:
түріндегі интегралдар. Мұнда келесі рекурентті формулаларды пайдалану керек:
1.
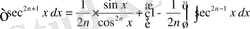 ,
,
2.
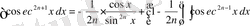 .
.
6)
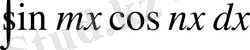 ,
,
 ,
,
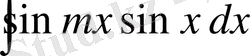 түріндегі интегралдар.
түріндегі интегралдар.
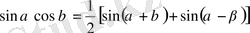 ,
,
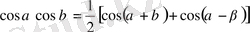 ,
,
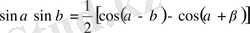
тригонометриялық формулалары тригонометриялық функциялардың көбейтіндісін қосынды түрінде өрнектеуге мүмкіндік береді.
7) Тригонометриялық алмастырулар.
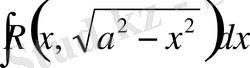 ,
,
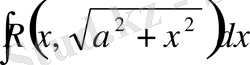 ,
,
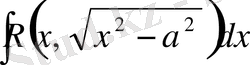 түріндегі интегралдар тиісті тригонометриялық алмастырулардың көмегімен
түріндегі интегралдар тиісті тригонометриялық алмастырулардың көмегімен
 және
және
 функцияларына қатысты рационал функциядан алынатын интегралға келтіріледі: бірінші интеграл үшін
функцияларына қатысты рационал функциядан алынатын интегралға келтіріледі: бірінші интеграл үшін
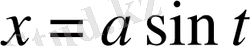 (немесе
(немесе
 ), екінші интеграл үшін
), екінші интеграл үшін
 (немесе
(немесе
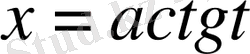 ) және үшінші интеграл үшін
) және үшінші интеграл үшін
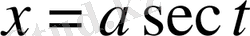 (немесе
(немесе
 ) .
) .
1. 2 Анықталған интеграл
1. Интегралдық қосындылар және анықталған интеграл
Айталық,
 функциясы
функциясы
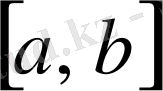 сегментінде
сегментінде
 анықталған болсын.
анықталған болсын.
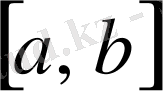 сегментін
сегментін
 нүктелерімен еркінше
нүктелерімен еркінше
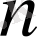
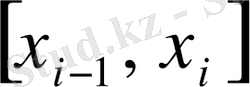 дербес сегменттерге бөлшектеуді
дербес сегменттерге бөлшектеуді
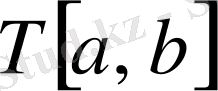 немесе
немесе
 символымен белгілейік.
символымен белгілейік.
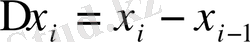 болсын. Әрбір
болсын. Әрбір
 сегментінде
сегментінде
 қалауымызша таңдап алып келесі қосындыны құрайық:
қалауымызша таңдап алып келесі қосындыны құрайық:
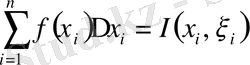 (1)
(1)
Анықтама.
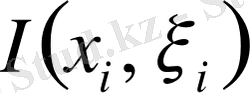 саны
саны
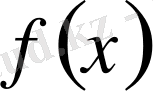 функциясының
функциясының
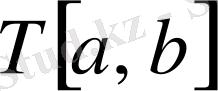 бөлшектеуіне және
бөлшектеуіне және
 сегменттерінен
сегменттерінен
 қалауымызша таңдапалуға сәйкес
Риман интегралдық қосындысы
деп аталады.
қалауымызша таңдапалуға сәйкес
Риман интегралдық қосындысы
деп аталады.
 белгілеуін енгізейік, бұл бөлшектеудің ұсаұтығы деп аталады.
белгілеуін енгізейік, бұл бөлшектеудің ұсаұтығы деп аталады.
Анықтама.
Егер
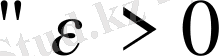 үшін барлық
үшін барлық
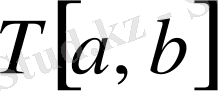 бөлшектеуіндегі
бөлшектеуіндегі
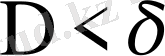 болатындай
болатындай
 саны табылып
саны табылып
 аралығында қалауымызша алынған кез келген
аралығында қалауымызша алынған кез келген
 нүктесі үшін
нүктесі үшін
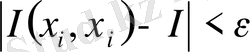
теңсіздігі орындалса, онда
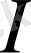
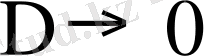 ұмтылғанда
ұмтылғанда
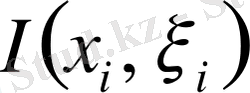 интегралдық қосындының шегі деп аталады, яғни
интегралдық қосындының шегі деп аталады, яғни
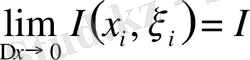 болады.
болады.
Анықтама.
Егер
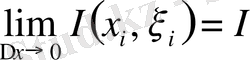 табылса, онда
табылса, онда
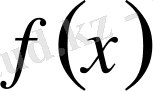 функциясы
функциясы
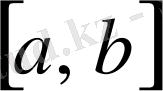 сегментінде Риман бойынша интегралданады дейді және де
сегментінде Риман бойынша интегралданады дейді және де
 саны
саны
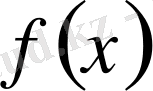 функциясының
функциясының
 сегменті бойынша Риман (анықталған) интегралы деп аталады және ол былай белгіленеді:
сегменті бойынша Риман (анықталған) интегралы деп аталады және ол былай белгіленеді:
 (2)
(2)
 және
және
 сандары интегралдаудың сйкесінше төменгі және жоғарғы шектері деп аталады.
сандары интегралдаудың сйкесінше төменгі және жоғарғы шектері деп аталады.
Геометриялық тұрғыдан алғанда, егер
 кесіндісінде
кесіндісінде
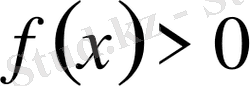 болса, онда
болса, онда
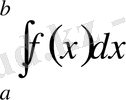 интегралы
интегралы
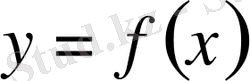 ,
,
 ,
,
 ,
,
 қисықтарымен шектелген фигура - қисық сызықты трапецияның ауданын анықтайды.
қисықтарымен шектелген фигура - қисық сызықты трапецияның ауданын анықтайды.
2. Жоғарғы және төменгі Дарбу қосындылары
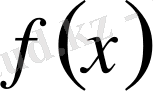 функциясы
функциясы
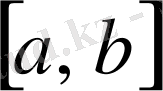 сегментінде анықталған және шенелген болсын. Еркінше
сегментінде анықталған және шенелген болсын. Еркінше
бөлшектеу
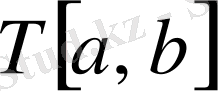 үшін
үшін
 ,
,
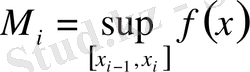 белгілеулерін енгізейік
белгілеулерін енгізейік
және келесі қосындыларды қарастырайық:
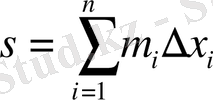 ,
,
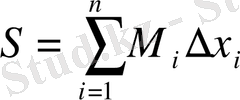 ,
,
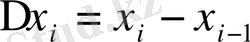 .
.
 және
және
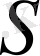 сандары берілген
сандары берілген
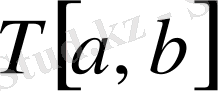 бөлшектеуіне сәйкес
бөлшектеуіне сәйкес
 функциясының төменгі және жоғарғы Дарбу қосындылары деп аталады.
функциясының төменгі және жоғарғы Дарбу қосындылары деп аталады.
Белгілі бір бөлшектеу
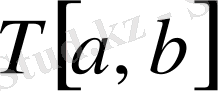 және осы бөлшектеудегі кез келген аралық нүктелер үшін
және осы бөлшектеудегі кез келген аралық нүктелер үшін
 .
.
Дарбу қосындыларының қасиеттері
1) Кез келген белгілі бір бөлшектеу үшін
 нүктелерінің барлық жиындары бойынша
нүктелерінің барлық жиындары бойынша
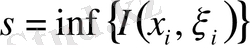 ,
,
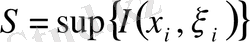 .
.
2) Егер
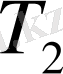 бөлшектеуі
бөлшектеуі
 бөлшектеуінен бірнеше нүктелерді қосу арқылы алынса (яғни
бөлшектеуінен бірнеше нүктелерді қосу арқылы алынса (яғни
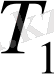 -ді ұсақтау арқылы алынса), онда
-ді ұсақтау арқылы алынса), онда
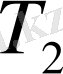 бөлшектеуінің
бөлшектеуінің
 төменгі қосындысы
төменгі қосындысы
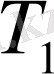 бөлшектеуінің
бөлшектеуінің
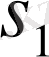 төменгі қосындысынан кем емес, ал
төменгі қосындысынан кем емес, ал
 бөлшектеуінің
бөлшектеуінің
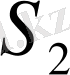 жоғарғы қосындысы
жоғарғы қосындысы
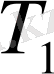 бөлшектеуінің
бөлшектеуінің
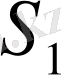 жоғарғы қосындысынан артық емес:
жоғарғы қосындысынан артық емес:
 ,
,
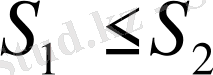 .
.
3) Еркінше бөлшектеудің төменгі қосындысы кез келген басқа бөлшектеудің жоғарғы қосындысынан аспайды.
4)
 және
және
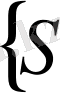 - кез келген бөлшектеу
- кез келген бөлшектеу
 үшін барлық төменгі және жоғарғы қосындылардың жиыны болсын, онда барлық бөлшектеулер бойынша
үшін барлық төменгі және жоғарғы қосындылардың жиыны болсын, онда барлық бөлшектеулер бойынша
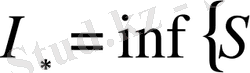 ,
,

сандары сәйкес жоғарғы және төменгі Дарбу интегралдары деп аталады. Төменгі Дарбу интегралы жоғарғы Дарбу интегралынан аспайды.
5) Дарбу леммасы.
 ,
,
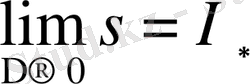 .
.
Теорема.
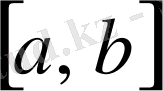 сегментінде шенелген
сегментінде шенелген
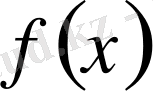 функциясы осы сегментте интегралданатын болуы үшін
функциясы осы сегментте интегралданатын болуы үшін
 болуы қажет және жеткілікті.
болуы қажет және жеткілікті.
3. Анықталған интегралдардың қасиеттері
1) Анықтама бойынша
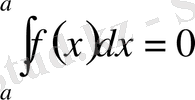
2) Анықтама бойынша
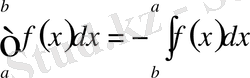
3)
Интегралдың сызықтығы.
Егер
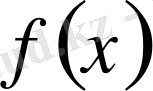 және
және
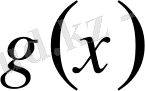 функциялары
функциялары
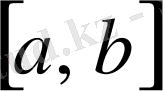 кесіндісінде интегралданатын болса,
кесіндісінде интегралданатын болса,
 және
және
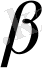 кез келген нақты сандар болса, онда
кез келген нақты сандар болса, онда
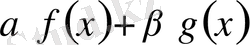 функциясы да
функциясы да
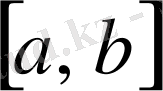 кесіндісінде интегралданадыжәне де төмендегідей анықталады:
кесіндісінде интегралданадыжәне де төмендегідей анықталады:
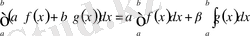 .
.
4) Егер
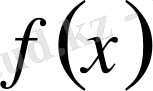 функциясы
функциясы
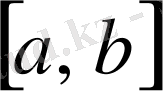 кесіндісінде интегралданса, онда
кесіндісінде интегралданса, онда
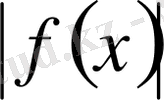 функциясы да
функциясы да
 кесіндісінде интегралданады және де
кесіндісінде интегралданады және де
 .
.
5) Егер
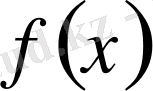 және
және
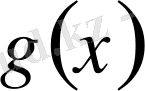 функциялары
функциялары
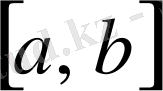 кесіндісінде интегралданса, онда
кесіндісінде интегралданса, онда
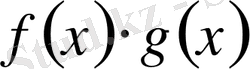 функциясы да
функциясы да
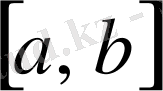 кесіндісінде интегралданады.
кесіндісінде интегралданады.
6) Егер
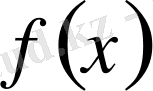 функциясы
функциясы
 кесіндісінде интегралданса, онда ол кез келген
кесіндісінде интегралданса, онда ол кез келген
 кесіндісінде интегралданады.
кесіндісінде интегралданады.
7)
Интегралдың аддитивтігі.
Егер
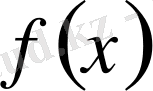 функциясы
функциясы
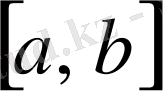 кесіндісінде интегралданатын болса және
кесіндісінде интегралданатын болса және
 болса, онда
болса, онда
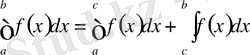 .
.
8) Егер
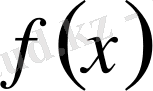 функциясы
функциясы
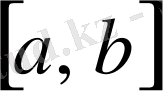 кесіндісінде интегралданатын болса және
кесіндісінде интегралданатын болса және
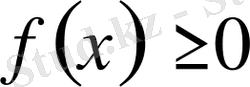 болса, онда
болса, онда
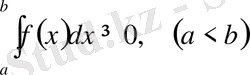 .
.
9) Егер
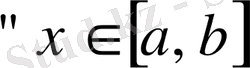 үшін
үшін
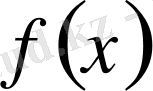 және
және
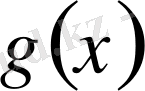 функциялары
функциялары
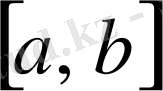 кесіндісінде интегралданатын болса және
кесіндісінде интегралданатын болса және
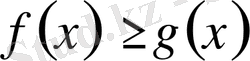 болса, он да
болса, он да
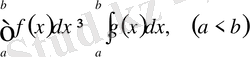 .
.
10) Егер
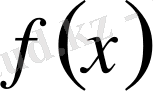 функциясы
функциясы
 сегментінде үзіліссіз болса,
сегментінде үзіліссіз болса,
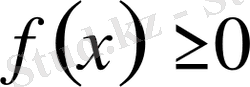 және ос ы
және ос ы
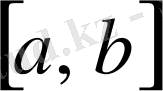 сегментінде
сегментінде
 болса, онда
болса, онда
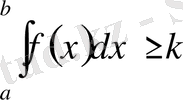 теңсіздігін қанағаттандыратын
теңсіздігін қанағаттандыратын
 саны табылады.
саны табылады.
4. Орта мән туралы теорема.
1-теорема.
Айталық, Егер
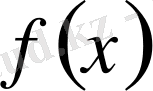 және
және
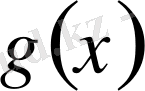 функциялары
функциялары
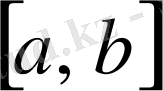 кесіндісінде интегралданатын болсын,
кесіндісінде интегралданатын болсын,
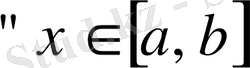 үшін
үшін
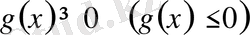 ,
,
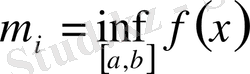 ,
,
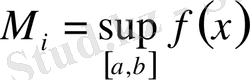 болсын, онда
болсын, онда
 (3)
(3)
теңдеуін қанағаттандыратын
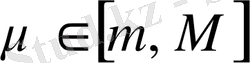 саны табылады.
саны табылады.
1-салдар
. Егер (3) формулада
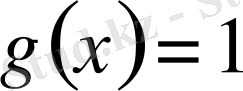 десек, онда
десек, онда
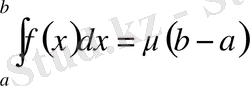 , мұнда
, мұнда
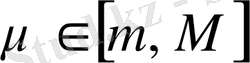 .
.
 саны
саны
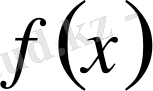 функциясының
функциясының
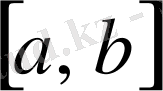 сегментіндегі орта мәні деп аталады, яғни
сегментіндегі орта мәні деп аталады, яғни
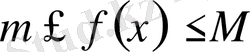 болса, онда
болса, онда
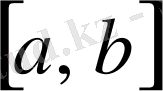 сегментінде
сегментінде
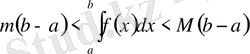 орындалады.
орындалады.
2-салдар.
Егер 1-теореманың шарттары орындалса және
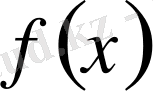 функциясы үзіліссіз болса, онда
функциясы үзіліссіз болса, онда
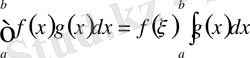 теңдігін қанағаттандыратын
теңдігін қанағаттандыратын
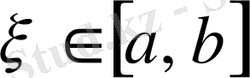 саны табылады.
саны табылады.
3-салдар.
Егер
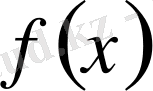 функциясы
функциясы
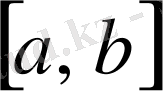 сегментінде үзіліссіз болса, онда
сегментінде үзіліссіз болса, онда
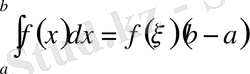 теңдігін қанағаттандыратын
теңдігін қанағаттандыратын
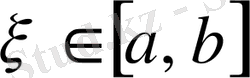 саны табылады.
саны табылады.
5. Жоғарғы шегі айнымалы анықталған интеграл
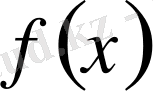 функциясы
функциясы
 сегментінде интегралданатын болсын,
сегментінде интегралданатын болсын,
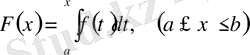 функциясы жоғарғы шегі айнымалы интеграл деп аталады.
функциясы жоғарғы шегі айнымалы интеграл деп аталады.
Теорема.
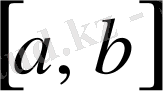 сегментінде үзіліссіз
сегментінде үзіліссіз
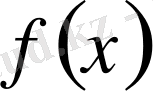 функциясының осы сегментте алғашқы функциясы болады. Ол алғашқы функциялардың бірі:
функциясының осы сегментте алғашқы функциясы болады. Ол алғашқы функциялардың бірі:
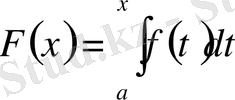 (4)
(4)
Ескерту.
Жоғарғы шегі айнымалы интеграл кез келген
 сегментінде интегралданатын
сегментінде интегралданатын
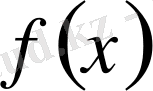 функциясы үшін анықталады, бірақ (4) түрде
функциясы үшін анықталады, бірақ (4) түрде
 функциясы
функциясы
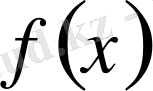 функциясының алғашқы функциясы болу үшін,
функциясының алғашқы функциясы болу үшін,
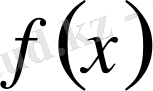 функциясы үзіліссіз болу керек.
функциясы үзіліссіз болу керек.
Енді интегралданатын функцияның алғашқы функциясы болмайтынын көрсететін мысал келтірейік:
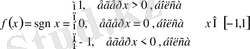
Бұл функция
 сегментінде интегралданады, бірақ оның алғашқы функциясы болмайды.
сегментінде интегралданады, бірақ оның алғашқы функциясы болмайды.
Анықтама.
Егер 1)
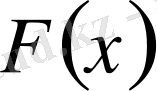 функциясы
функциясы
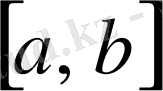 сегментінде үзіліссіз, 2)
сегментінде үзіліссіз, 2)
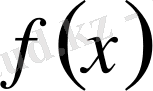 функциясының үзіліссіздік нүктелерінде
функциясының үзіліссіздік нүктелерінде
 болса, онда
болса, онда
 функциясы
функциясы
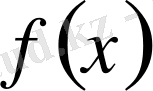 функциясының
функциясының
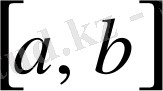 сегментіндегі алғашқы функциясы деп аталады.
сегментіндегі алғашқы функциясы деп аталады.
6. Анықталған интегралды есептеу ережелері
1) Ньютон-Лейбниц формуласы:
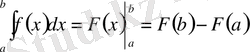 , мұнда
, мұнда
 -
-
 функциясының алғашқы функциясы, яғни
функциясының алғашқы функциясы, яғни
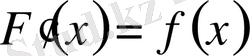 .
.
2) Айнымалыларды алмастырып интегралдау.
а)
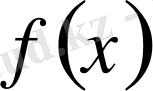 функциясы
функциясы
 сегментінде анықталған және үзіліссіз болсын;
сегментінде анықталған және үзіліссіз болсын;
б)
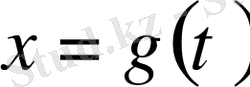 функциясы
функциясы
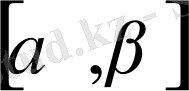 сегментінде өзінің туындысымен бірге анықталған және үзіліссіз болсын, мұнда
сегментінде өзінің туындысымен бірге анықталған және үзіліссіз болсын, мұнда
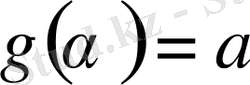
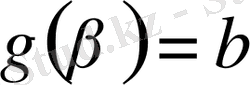 және
және
 болсын. Сонда
болсын. Сонда
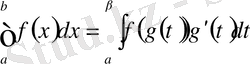 .
.
3) Бөліктеп интегралдау.
Егер
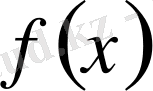 және
және
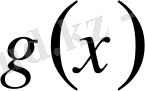 функцияларының
функцияларының
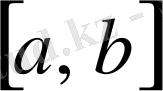 сегментінде үзіліссіз туындылары бар болса, онда
сегментінде үзіліссіз туындылары бар болса, онда
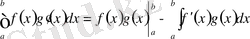 .
.
4) Егер
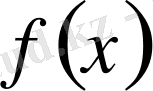 тақ функция, яғни
тақ функция, яғни
 болса, онда
болса, онда
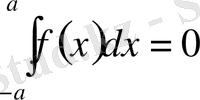 . Егер
. Егер
 жұп функция, яғни
жұп функция, яғни
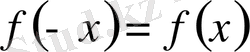 болса, онда
болса, онда
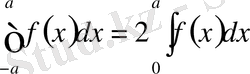 .
.
1. 3 Анықталған интегралдың қолданулары
1. Доғаның ұзындығын есептеу
Егер
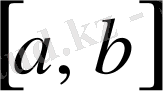 кесіндісінде берілген
кесіндісінде берілген
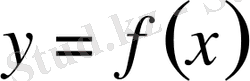 қисығы жатық болса (яғни
қисығы жатық болса (яғни
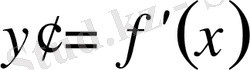 туындысы үзіліссіз), онда осы қисықтың сәйкес доғасының ұзындығы келесі формула бойынша есептеледі:
туындысы үзіліссіз), онда осы қисықтың сәйкес доғасының ұзындығы келесі формула бойынша есептеледі:
 .
.
Егер қисық параметрлі түрде берілсе, яғни
 (
(
 -үзіліссіз дифференциалданатын функциялар), онда доғаның
-үзіліссіз дифференциалданатын функциялар), онда доғаның
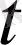 параметрінің
параметрінің
 -ден
-ден
 -ге дейін монотонды өзгеруіне сәйкес келетін ұзындығы мына формула бойынша есептеледі:
-ге дейін монотонды өзгеруіне сәйкес келетін ұзындығы мына формула бойынша есептеледі:
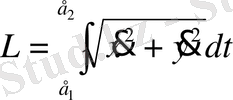 .
.
Егер
 жатық(тегіс) қисық полярлық координаталар арқылы берілсе, онда доғаның ұзындығы
жатық(тегіс) қисық полярлық координаталар арқылы берілсе, онда доғаның ұзындығы
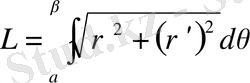
болады.
2. Жазық фигураның ауданын есептеу
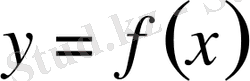
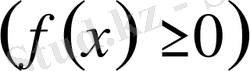 қисығымен,
қисығымен,
 және
және
 түзулерімен және
түзулерімен және
 осінің
осінің
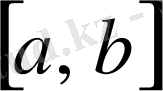 кесіндісімен шектелген қисық сызықты трапецияның ауданы келесі формула бойынша есептеледі:
кесіндісімен шектелген қисық сызықты трапецияның ауданы келесі формула бойынша есептеледі:

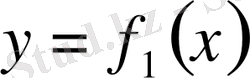 және
және
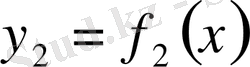
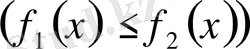 қисықтарымен және
қисықтарымен және
 және
және
 түзулерімен шектелген фигураның ауданы келесі формула бойынша есептеледі:
түзулерімен шектелген фигураның ауданы келесі формула бойынша есептеледі:
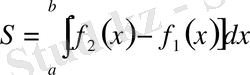 .
.
Егер қисық
 және
және
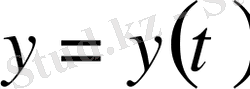 параметрлік теңдеулерімен берілсе, онда
параметрлік теңдеулерімен берілсе, онда
 ,
,
 түзулерімен және
түзулерімен және
 осінің
осінің
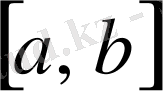 кесіндісімен шектелген қисық сызықты трапецияның ауданы келесі формуламен өрнектеледі:
кесіндісімен шектелген қисық сызықты трапецияның ауданы келесі формуламен өрнектеледі:
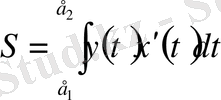
мұнда
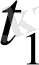 және
және
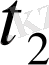
 ,
,
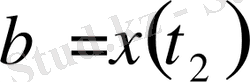 теңдеулерімен анықталады,
теңдеулерімен анықталады,
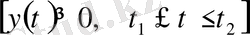 .
.
Полярлық координаталар арқылы берілген
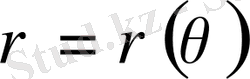 теңдеуімен және
теңдеуімен және
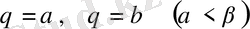 екі полярлық радиустармен берілген қисық сызықты сектордың ауданы келесі формула бойынша есептеледі:
екі полярлық радиустармен берілген қисық сызықты сектордың ауданы келесі формула бойынша есептеледі:

3. Қисықтың айналуынан пайда болған беттердің ауданын есептеу.
Егер
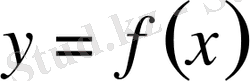
 тегіс қисығының доғасы
тегіс қисығының доғасы
 осінен айналса, онда айналудан пайда болған беттің ауданы келесі формуламен есептеледі:
осінен айналса, онда айналудан пайда болған беттің ауданы келесі формуламен есептеледі:
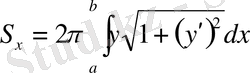 .
.
Егер қисық
 және
және
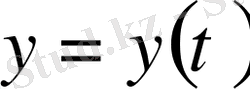
 параметрік теңдеулерімен берілсе, онда
параметрік теңдеулерімен берілсе, онда
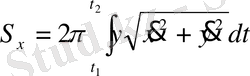 .
.
4. Денелердің көлемін табу
а) Көлденең қимасының ауданы бойынша дененің көлемін есептеу
Егер дененің
 осіне перпендикуляр жазықтықпен қиғандағы көлденең қимасының ауданын
осіне перпендикуляр жазықтықпен қиғандағы көлденең қимасының ауданын
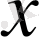 -ке байланысты функция ретінде өрнектеуге болса, яғни
-ке байланысты функция ретінде өрнектеуге болса, яғни
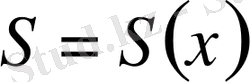
 , онда
, онда
 және
және

 осіне перпендикуляр екі жазықтықтың арасында жатқан дене бөлігінің көлемі төмендегі формула арқылы табылады:
осіне перпендикуляр екі жазықтықтың арасында жатқан дене бөлігінің көлемі төмендегі формула арқылы табылады:
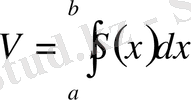 .
.
б) Айналу денесінің көлемін есептеу
Егер
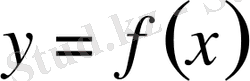 қисығымен және
қисығымен және
 ,
,
 ,
,
 түзулерімен шектелген трапеция
түзулерімен шектелген трапеция
 осінен айналса, онда айналу денесінің көлемі келесі формуламен есептеледі:
осінен айналса, онда айналу денесінің көлемі келесі формуламен есептеледі:
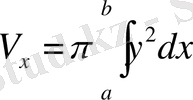 . ер
. ер
 және
және
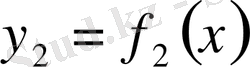
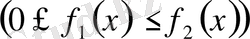 қисықтарымен және
қисықтарымен және
 ,
,
 түзулерімен шектелген фигура
түзулерімен шектелген фигура
 осінен айналса, онда айналу денесінің көлемі төмендегідей болады:
осінен айналса, онда айналу денесінің көлемі төмендегідей болады:
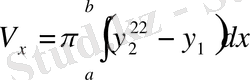 .
.
5. Физикалық және механикалық есептер
а) Жазық доғалар мен фигуралардың статикалақ моменттері
және инерциялық моменті.
Айталық,
 жазықтығында массалары
жазықтығында массалары
 болатын
болатын
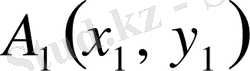 ,
,
 , . . . ,
, . . . ,
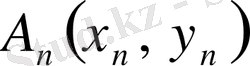 материялық нүктелер жүйесі берілсін. Осы жүйенің
материялық нүктелер жүйесі берілсін. Осы жүйенің
 осіне қатысты статикалық моменті
осіне қатысты статикалық моменті
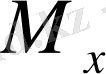 деп осы нүктелердің массаларының олардың ординаталарына көбейтінділерінің қосындысын айтады:
деп осы нүктелердің массаларының олардың ординаталарына көбейтінділерінің қосындысын айтады:
 .
.
Осылайша жүйенің
 осіне қатысты статикалық моменті
осіне қатысты статикалық моменті
 анықталады:
анықталады:
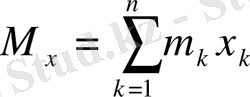 .
.
Жүйенің
 және
және
 осьтеріне қатысты
осьтеріне қатысты
 және
және
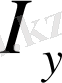 инерциялық моменттері деп нүктелердің массаларының олардың сәйкес осьтен қашықтықтарының квадратына көбейтінділерінің қосындыларын айтады. Сонымен,
инерциялық моменттері деп нүктелердің массаларының олардың сәйкес осьтен қашықтықтарының квадратына көбейтінділерінің қосындыларын айтады. Сонымен,
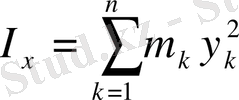 ,
,
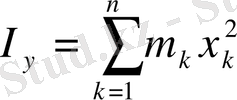 .
.

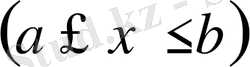 тегіс қисығының доғасының статикалық моменті мен инерция моменті келесі формулалар бойынша есептеледі:
тегіс қисығының доғасының статикалық моменті мен инерция моменті келесі формулалар бойынша есептеледі:
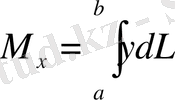 ,
,
 ,
,
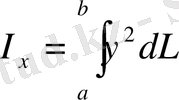 ,
,
 .
.
мұнда
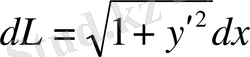 - қисық доғасының дифференциалы.
- қисық доғасының дифференциалы.
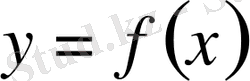 қисығымен
қисығымен
 осімен және
осімен және
 ,
,
 түзулерімен шектелген қисық сызықты трапецияның статикалық моменті мен инерция моменті келесі формулалар бойынша есептеледі:
түзулерімен шектелген қисық сызықты трапецияның статикалық моменті мен инерция моменті келесі формулалар бойынша есептеледі:
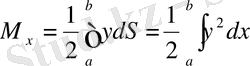 ,
,
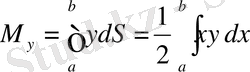 ,
,
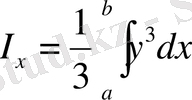 ,
,
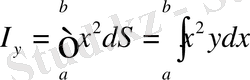 .
.
Бұл формулалардағы
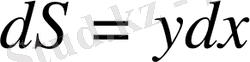 - қисық сызықты трапецияның ауданының дифференциалы.
- қисық сызықты трапецияның ауданының дифференциалы.
б) Ауырлық центрінің координаталарын табу

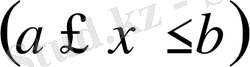 жазық қисығының біртекті доғасының ауырлық центрінің координаталары келесі формулалар бойынша өрнектеледі:
жазық қисығының біртекті доғасының ауырлық центрінің координаталары келесі формулалар бойынша өрнектеледі:
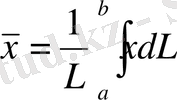 ,
,
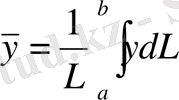 ,
,
Мұнда
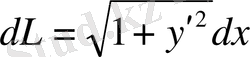 , ал
, ал
 -доғаның ұзындығы.
-доғаның ұзындығы.
Қисық сызықты трапецияның ауырлық центрінің координаталары келесі формулалар бойынша есептеледі:
 ,
,
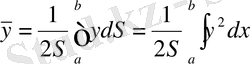 ,
,
мұнда
 , ал
, ал
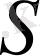 -фигураның ауданы.
-фигураның ауданы.
МЕНШІКСІЗ ИНТЕГРАЛДАР
1. Негізгі ұғымдар
Меншіксіз интегралдар деп 1) шектері шексіз интегралдарды 2) шексіз функциялардан алынған интегралдарды айтады.
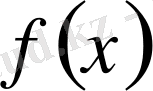 функциясының
функциясының
 -дан
-дан
 -ке дейінгі меншіксіз интеграл
-ке дейінгі меншіксіз интеграл
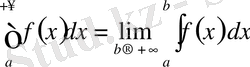
формуласы бойынша есептелінеді.
Егер бұл шек анықталса және ақырлы болса, онда меншіксіз интеграл жинақталады дейді, ал егер шек табылмаса немесе шексіздікке тең болса, онда жинақталмайды дейді. Сол сиқты
 ;
;
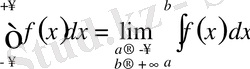 .
.
Егер
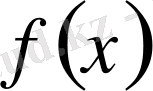 функциясы
функциясы
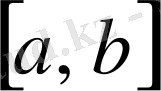 кесіндісінің
кесіндісінің
 нүктесінде шексіз үзілісті болса және
нүктесінде шексіз үзілісті болса және
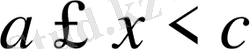 және
және
 болғанда үзіліссіз болса, онда анықтама бойынша
болғанда үзіліссіз болса, онда анықтама бойынша
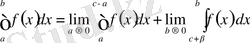 .
.
Егер теңдіктің оң жағындағы екі шек те табылса, онда
 (мұнда
(мұнда
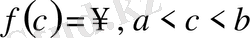 ) меншіксіз интегралы жинақталады дейді, ал егер бұл шектердің ең болмағанда біреуі табылмаса, онда жинақталмайды дейді.
) меншіксіз интегралы жинақталады дейді, ал егер бұл шектердің ең болмағанда біреуі табылмаса, онда жинақталмайды дейді.
2. Салыстыру белгілері
Меншіксіз интегралдардың жинақтылығын зерттеген кезде келесі салыстыру белгілерінің біреуін пайдаланады:
1. Егер барлық
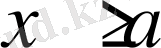 үшін
үшін
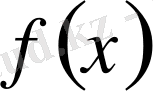 және
және
 функциялары анықталса және
функциялары анықталса және
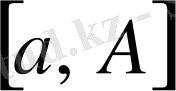 кесіндісінде интегралданса, мұнда
кесіндісінде интегралданса, мұнда
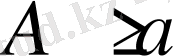 және барлық
және барлық
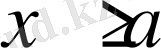 үшін
үшін
 болса, онда
болса, онда
 интегралының жинақтылығынан
интегралының жинақтылығынан
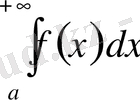 интегралының жинақтылығы шығады және де
интегралының жинақтылығы шығады және де
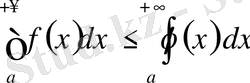 .
.
2. (а) Егер
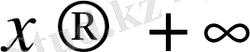 кезде
кезде
 функциясы
функциясы
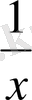 -пен салыстырғанда
-пен салыстырғанда
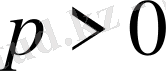 ретті шексіз аз шама болса, онда
ретті шексіз аз шама болса, онда
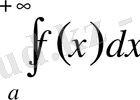 интегралы
интегралы
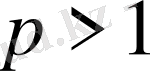 болғанда жинақталады және
болғанда жинақталады және
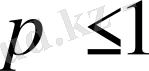 болғанда жинақталмайды.
болғанда жинақталмайды.
(б) Егер
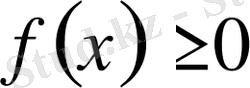 функциясы
функциясы
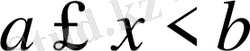 аралығында анықталған және үзіліссіз болса және
аралығында анықталған және үзіліссіз болса және
 кезде
кезде
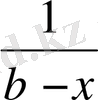 -пен салыстырғанда
-пен салыстырғанда
 ретті шексіз үлкен шама болса, онда
ретті шексіз үлкен шама болса, онда
 интегралы
интегралы
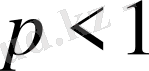 болған кезде жинақталады, ал
болған кезде жинақталады, ал
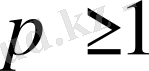 болған кезде жинақталмайды.
болған кезде жинақталмайды.
Мысалы, 1)
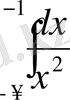 - есептеңіз.
- есептеңіз.
Шешуі:
 , яғни меншіксіз интеграл жинақталады.
, яғни меншіксіз интеграл жинақталады.
2)
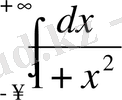 - есептеңіз
- есептеңіз
Шешуі: Интеграл астындағы функция жұп, сондықтан
 . Сонда
. Сонда
 .
.
Олай болса,
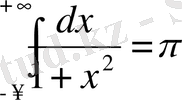 , яғни меншіксіз интеграл жинақталады.
, яғни меншіксіз интеграл жинақталады.
3)
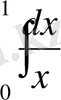 - есептеңіз.
- есептеңіз.
Интеграл астындағы функция
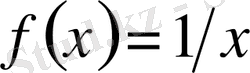
 нүктесінде шексіз. Сондықтан,
нүктесінде шексіз. Сондықтан,
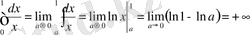 . Демек, меншіксіз интеграл жинақтамайды.
. Демек, меншіксіз интеграл жинақтамайды.
Еселі интегралдардың қолданулары.
Қисық сызықты интегралдар.
1. Тікбұрышты координаталармен берілген екі еселі интеграл
Айталық,
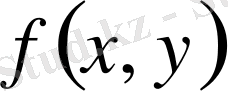 функциясы
функциясы
 жазықтығының
жазықтығының
 шенелген облысында анықталсын.
шенелген облысында анықталсын.
 облысын аудандары
облысын аудандары
 және диаметрлері
және диаметрлері
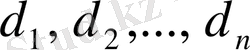 (лблыстың диаметрі деп осы облыстың шекарасының ең қашақ екі нүктесінің арасының ұзындығын айтады) болатын "
(лблыстың диаметрі деп осы облыстың шекарасының ең қашақ екі нүктесінің арасының ұзындығын айтады) болатын "
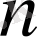 " облыстарға бөлшектейік. Әрбір элементар облыста кез келген
" облыстарға бөлшектейік. Әрбір элементар облыста кез келген
 нүктесін таңдап алайық және функцияның
нүктесін таңдап алайық және функцияның
 нүктесіндегі мәнін осы облыстың ауданына көбейтейік.
нүктесіндегі мәнін осы облыстың ауданына көбейтейік.
 функциясы үшін
функциясы үшін
 облысы бойынша
интегралдық қосынды
деп келесі қосындыны айтады:
облысы бойынша
интегралдық қосынды
деп келесі қосындыны айтады:
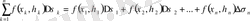 (1)
(1)
Егер
 ұмтылғанда интегралдық қосындының
ұмтылғанда интегралдық қосындының
 облысын элементар бөлшектерге бөлу әдісінен және осы облыста
облысын элементар бөлшектерге бөлу әдісінен және осы облыста
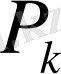 нүктелерін таңдап алудан тәуелсі анықталған ақырлы шегі болса, яғни
нүктелерін таңдап алудан тәуелсі анықталған ақырлы шегі болса, яғни
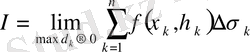 (2)
(2)
онда бұл шек
 облысындағы
облысындағы
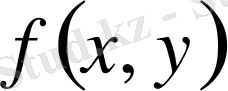 функциясының
екі еселі интегралы
деп аталады және былай белгіленеді:
функциясының
екі еселі интегралы
деп аталады және былай белгіленеді:
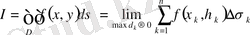 (3)
(3)
Ескерту. Егер
 облысында
облысында
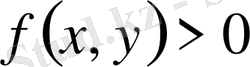 болса, онда
болса, онда
 екі еселі интеграл - жоғарыдан
екі еселі интеграл - жоғарыдан
 бетімен, бүйірінен құраушылары
бетімен, бүйірінен құраушылары
 осімен параллель болатвн цилиндрлік бетпен және төменнен
осімен параллель болатвн цилиндрлік бетпен және төменнен
 жазақтығының
жазақтығының
 облысымен шектелген цилиндрлік дененің көлеміне тең болады.
облысымен шектелген цилиндрлік дененің көлеміне тең болады.
Екі еселі интегралдың негізгі қасиеттері
 .
.
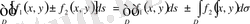
 .
.
 , мұнда
, мұнда
 - тұрақты сан.
- тұрақты сан.
 . Егер
. Егер
 интегралдау облысы
интегралдау облысы
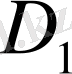 және
және
 облыстарына бөлінсе, онда
облыстарына бөлінсе, онда
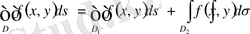
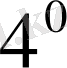 .
Екі еселі интегралды бағалау.
Егер
.
Екі еселі интегралды бағалау.
Егер
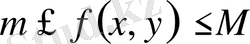 болса, онда
болса, онда
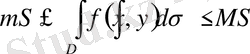 , мұнда
, мұнда
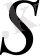 -
-
 облысының ауданы, ал
облысының ауданы, ал
 және
және
 -
-
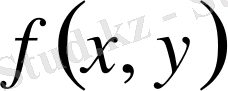 функциясының
функциясының
 облысындағы сәйкес ең кіші және ең үлкен мәндері.
облысындағы сәйкес ең кіші және ең үлкен мәндері.
Екі еселі интегралдарды есептеу ережелері
Интегралдау облысының негізгі екі түрі болады.
1.
 интегралдау облысы сол жақтан және оң жақтан
интегралдау облысы сол жақтан және оң жақтан
 ,
,
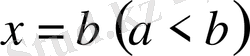 түзулерімен, ал төменнен және жоғарыдан әрқайсысы вертикаль түзумен тек бір нүктеде қиылысатын
түзулерімен, ал төменнен және жоғарыдан әрқайсысы вертикаль түзумен тек бір нүктеде қиылысатын
 және
және
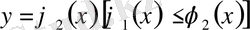 үзіліссіз қисықтармен шектелген.
үзіліссіз қисықтармен шектелген.
Мұндай облыс үшін екі еселі интеграл келесі формула бойынша есептеледі:
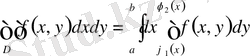
және де алдымен ішкі интеграл
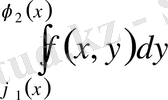 ,
,
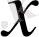 -ті тұрақты деп алып есептеледі.
-ті тұрақты деп алып есептеледі.
2.
 интегралдау облысы төменнен және жоғарыдан
интегралдау облысы төменнен және жоғарыдан
 және
және
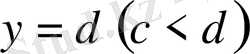 түзулерімен, ал сол жақтан және оң жақтан әрқайсысы горизонталь түзумен тек бір нүктеде қиылысатын үзіліссіз
түзулерімен, ал сол жақтан және оң жақтан әрқайсысы горизонталь түзумен тек бір нүктеде қиылысатын үзіліссіз
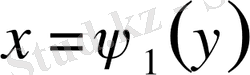 және
және
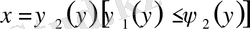 қисықтарымен шектелген.
қисықтарымен шектелген.
Мұндай облыс үшін екі еселі интеграл келесі формула бойынша есептеледі:

және де алдымен ішкі интеграл
 ,
,
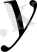 -ті тұрақты деп алып есептеледі.
-ті тұрақты деп алып есептеледі.
Көрсетілген формулалардың оң жақтары қайталанбалы интегралдар деп аталады. Жалпы жағдайда интегралдау облысы бөлшектеу жолымен жоғарыдағы негізгі интегралдарға келтіріледі
2. Екі еселі интегралда айнымалыларды ауыстыру
Полярлық координаталардағы екі еселі интеграл.
 тікбұрышты координаталарымен берілген екі еселі интегралды тікбұрышты координаталармен
тікбұрышты координаталарымен берілген екі еселі интегралды тікбұрышты координаталармен
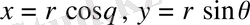 өрнектері арқылы байланысатын
өрнектері арқылы байланысатын
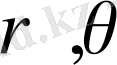 полярлық координаталарға көшіру келесі формула бойынша іске асырылады:
полярлық координаталарға көшіру келесі формула бойынша іске асырылады:
.
Егер
 интегралдау облысы полюстен басталатын
интегралдау облысы полюстен басталатын
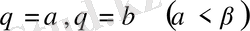 сәулелерімен және
сәулелерімен және
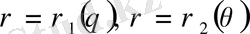 қисықтарымен (мұнда
қисықтарымен (мұнда
 және
және
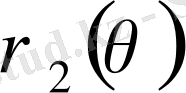 -
-
 және
және
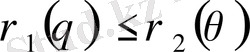 болғанда бірмәнді функциялар) шектелсе, онда екі еселі интеграл келесі формула бойынша есептеледі:
болғанда бірмәнді функциялар) шектелсе, онда екі еселі интеграл келесі формула бойынша есептеледі:
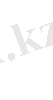

мұнда
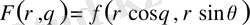 және де алдымен ішкі интеграл
және де алдымен ішкі интеграл
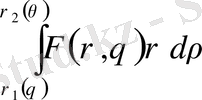 ,
,
 -ны тұрақты деп алып есептеледі.
-ны тұрақты деп алып есептеледі.
Қисық сызықты координаталардағы екі еселі интеграл.
Айталық екі еселі интеграл
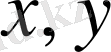 тікбұрышты координаталардан, осы тікбұрышты координаталармен
тікбұрышты координаталардан, осы тікбұрышты координаталармен
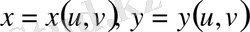 өрнектері арқылы байланысатын
өрнектері арқылы байланысатын
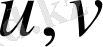 қисық сызықты координаталарға ауыстырылсын, мұнда
қисық сызықты координаталарға ауыстырылсын, мұнда
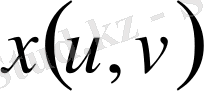 және
және
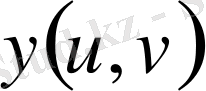 функцияларының
функцияларының
 жазықтығының
жазықтығының
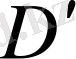 облысында үзіліссіз дербес туындылары бар және түрлендірудің якобиан деп аталатын анықтауышы
облысында үзіліссіз дербес туындылары бар және түрлендірудің якобиан деп аталатын анықтауышы
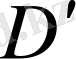 облысында нөлге тең емес:
облысында нөлге тең емес:
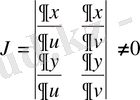
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz