Логарифмдік теңдеулер мен теңсіздіктерді шешу әдістері, мысалдары және жаттығулары


Логарифмдік теңдеулерді және теңсіздіктерді шешу
Ең қарапайым логарифмдік теңдеуді қарастырайық
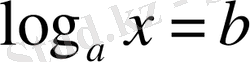 .
Логарифмдік функция (0; ∞) аралығында өседі (не кемиді) және осы аралықта барлық нақты сандарды қабылдайды. Түбір туралы теорема бойынша, бұдан кез келген
b
үшін берілген теңдеудің түбірі бар және ол тек біреу ғана болатындығы шығады. Санның логарифмінің анықтамасынан
а
b
саны сол шешім екендігі бірден табылады.
.
Логарифмдік функция (0; ∞) аралығында өседі (не кемиді) және осы аралықта барлық нақты сандарды қабылдайды. Түбір туралы теорема бойынша, бұдан кез келген
b
үшін берілген теңдеудің түбірі бар және ол тек біреу ғана болатындығы шығады. Санның логарифмінің анықтамасынан
а
b
саны сол шешім екендігі бірден табылады.
1-м ы с а л. Теңдеуді шешейік log 2 (х 2 + 4х + 3) = 3.
Берілген теңдеуді х -тің х 2 + 4х + 3 = 2 3 теңдігі орындалатындай мәндері ғана қанағаттандырады. Сонымен, х 2 + 4х + 5 = 0 квадрат теңдеу шықты. Оның түбірлері: 1 мен - 5 сандары. Олай болса, берілген теңдеудің шешімі екі сан, олар: 1 мен - 5.
2-м ы с а л. Теңдеуді шешейік log 5 (2 х + 3) =log 5 ( х + 1) . Бұл теңдеу х -тің тек 2х + 3 > 0 және х + 1 > 0 теңсіздіктер орындалатындай мәндерінде ғана анықталады. х -тің мәндері үшін берілген теңдеу 2х + 3 = х +1 теңдеуімен мәндес. Бұдан х = - 2 екенін табамыз. Ал х = -2 саны х+ 1 > 0 теңсіздігін қанағаттандырмайды. Олай болса, берілген теңдеудің түбірлері болмайды.
Ал осы теңдеуді басқаша шешуге болар еді. Берілген теңдеудің салдарына 2х + 3 = х + 1 ауысып, х = - 2 екенін табамыз. Теңдеулерді мәндестік бұзылмайтындай етіп түрлендірген жағдайда, табылған мәнді бастапқы теңдеуге қойып, тексеру қажет. Тап осы жағдайда log 5 (-1) =log 5 (-1) теңдігі тура емес (мұның мағынасы жоқ) .
3-м ы с а л. Теңдеуді шешейік log x ( х 2 -2х + 2) = 1.
Бұл теңдеуді х -тің тек х > 0 және х ≠ 1 (х - логарифмдік функцияның негізі) және х 2 -2х + 2= х, яғни х 2 -3х +2 = 0 теңдігі орындалатындай мәндері ғана қанағаттандырады. Осы табылған квадрат теңдеудің түбірлері 1 және 2 сандары болып табылады. Алайда х = 1 саны берілген теңдеудің шешімі бола алмайды. Олай болса, тек 2 саны ғана берілген теңдеудің шешімі болады.
4-м ы с а л. Теңсіздікті шешейік
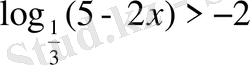 .
.
-2 саны
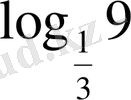 -іне тең. Сондықтан берілген теңсіздікті былай көшіріп жазуға болады:
-іне тең. Сондықтан берілген теңсіздікті былай көшіріп жазуға болады:
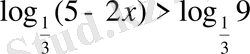 .
.
Негізі - логарифмдік функция R
+
жиынында анықталған және кемиді, өйткені
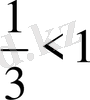 . Олай болса, екінші теңсіздікті 0 < 5 -
2х <
9 шарты орындалатындай
х
мәндері ғана қанағаттандырады, бұдан
- 2 < х < 2, 5 .
. Олай болса, екінші теңсіздікті 0 < 5 -
2х <
9 шарты орындалатындай
х
мәндері ғана қанағаттандырады, бұдан
- 2 < х < 2, 5 .
Сонымен, берілген теңсіздіктің шешімдер жиыны (-2; 2, 5) интервалы болмақ.
5-м ы с а л. Теңдеуді шешейік
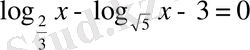 .
.
Екінші қосылғашты 5 негізіне көшіріп,
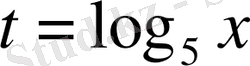 ауыстыруын жасаймыз, сонда
ауыстыруын жасаймыз, сонда
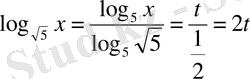
Енді берілген теңдеуді
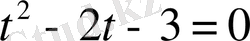 түрінде көшіріп жазуға болады. Бұл квадрат теңдеудің түбірлері 3 және - 1 сандары. Ауыстырылғаннан кейінгі log
5
х=
3 және log
5
x = -
1 теңндеулерін шешіп, мынаны табамыз:
х
= 5
3
= 125 және
х=5
-1
=0, 2.
түрінде көшіріп жазуға болады. Бұл квадрат теңдеудің түбірлері 3 және - 1 сандары. Ауыстырылғаннан кейінгі log
5
х=
3 және log
5
x = -
1 теңндеулерін шешіп, мынаны табамыз:
х
= 5
3
= 125 және
х=5
-1
=0, 2.
6-м ы с а л. Теңдеулер жүйесін шешейік:
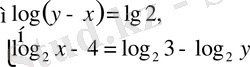
Жүйенің бірінші теңдеуі
у-х
= 2 теңдеуімен, ал екіншісі
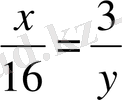 теңдеуімен мәндес және
х>0, у>0.
теңдеуімен мәндес және
х>0, у>0.
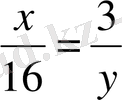 теңдеуіне
у = х + 2
қойып, табатынымыз:
х(х
+ 2) = 48, бұдан
х
2
+ 2
х -
48 = 0, яғни
х=
-
8 немесе
х
= 6. Ал
х
>0 болғандықтан,
х
= 6 шығады, ал ендеше,
у=
8. Сонымен, берілген теңдеулер жүйесінің шешімі біреу ғана:
х = 6, у = 8.
теңдеуіне
у = х + 2
қойып, табатынымыз:
х(х
+ 2) = 48, бұдан
х
2
+ 2
х -
48 = 0, яғни
х=
-
8 немесе
х
= 6. Ал
х
>0 болғандықтан,
х
= 6 шығады, ал ендеше,
у=
8. Сонымен, берілген теңдеулер жүйесінің шешімі біреу ғана:
х = 6, у = 8.
Енді тағы да a х = b (b > 0) түріндегі кез келген көрсеткіштік теңдеудің түбірін логарифмнің көмегімен жазуға болатынын ескерте кетейік. Ол түбірдің түрі мынадай: х = log a b .
7-м ы с а л. Теңдеуді шешейік 5 1-3 х = 7.
Логарифмнің анықтамасы бойынша
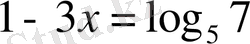 және
және
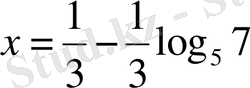 .
.
Жаттығулар
Теңдеуді шеш (512 - 515) .
512. а) 9 х = 0, 7 ; б) (0, 3) х = 7 ; в) 2 х = 10 ; г) 10 х = π .
513.
a) log
5
х
= 2; б) log
0, 4
х = -
1; в) log
9
х
=
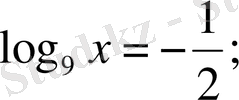 г)
г)
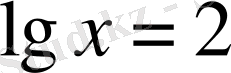
514.
a)
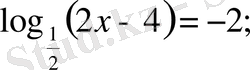 б) log
х
(
х
2
+
2х +
3) = log
х
6 .
б) log
х
(
х
2
+
2х +
3) = log
х
6 .
в) log 0, 3 (5 + 2х) = 1; г) log 2 (3 - х) = 0.
515. а) (0, 2) 4- х = 3 ; б) 5 х = 7 ; в) 3 2-3 х = 8 ; г) 7 2х = 4 .
Теңдікті шеш (516 - 517) .
516. a) log 3 х > 2 ; б) log 0, 5 х > - 2; в) log 0, 7 х < 1; г) log 2, 5 x < 2 .
517.
а) log
4
(
x
- 2) < 2; б)
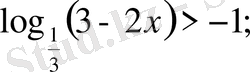
в) log
5
(3
x
+ 1) > 2; г)
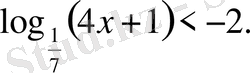
Теңдеуді шеш (518 - 520) .
518.
a) log
а
х
= 2 log
а
3 + log
а
5; б)
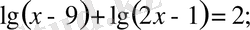
в)
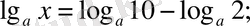 г)
г)
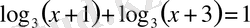 .
.
519.
a)
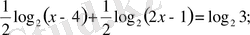
б)
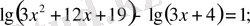
в)
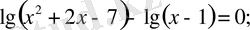
г)
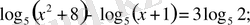
520.
a)

в)

521. Теңдеулер жүйесін шеш:
а)
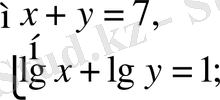 б)
б)
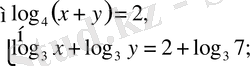
в)
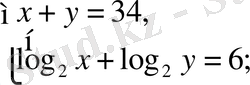 г)
г)
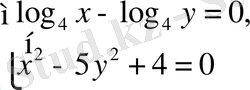
Теңдеуді шеш (522 - 524) .
522.
a)
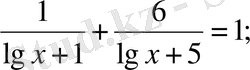 б)
б)
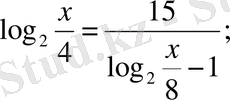
в)
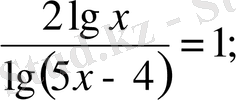 г)
г)
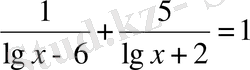
Сандарды салыстыр (501 -503) .
501.
а) log
2
3, 8 және log
2
4, 7; б)
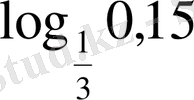 және
және
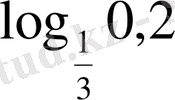 ;
;
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz