Тензор компоненттері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 16 бет
Таңдаулыға:

Курстық жұмыс
Тақырыбы; Тензорлар

Жоспар:
Кіріспе
1 Анықтамалар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
1.1 Қазіргі заманғы анықтама ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
1.2 Тензор көп сызықты функция ретінде ... ... ... ... ... ... ... ... ... ... ... ... ...
2 Тензор компоненттері ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ...
2.1 Классикалық анықтама туралы ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ...
3 Мысалдар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
4 Тензорлық операциялар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
5 Симметрия ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
6 Физикадағы тензорлар ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ...
Әдебиет ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..

Кіріспе

Тензор (латын тілінен tenus, уақыт) - сызықтық алгебраның объектісі. Тензорлардың ерекше жағдайлары скалярлар, векторлар, матрицалар және екі сызықты формалар болып табылады.

Көбінесе тензор көп өлшемді кесте ретінде ұсынылады d \ есе d \ есе \ cdots \ есе d (мұндағы d - тензор көрсетілген векторлық кеңістіктің өлшемі, ал факторлар саны тензор валенттілігімен сәйкес келеді) сандармен толтырылған (тензор компоненттері).

Мұндай бейнелеу (валенттілік тензорларын қоспағанда - скалярлар) тек базисті (немесе координаттар жүйесін) таңдағаннан кейін ғана мүмкін; базис өзгерген кезде тензор компоненттері белгілі бір жолмен өзгереді. Бұл жағдайда тензордың өзі геометриялық бірлік ретінде негізді таңдауға тәуелді емес. Мұны тензордың ерекше жағдайы болып табылатын вектордың мысалынан көруге болады: вектордың компоненттері координат осьтері өзгерген кезде өзгереді, бірақ вектордың өзі - визуалды бейнесі жай ғана сызылған көрсеткі бола алады - бұдан өзгермейді.

Тензор термині сонымен қатар көбінесе тензор есебімен зерттелетін тензор өрісі терминінің аббревиатурасы болып табылады.

Анықтамалар

1.1. Қазіргі заманғы анықтама
D өлшемді V векторлық кеңістіктегі рангтің тензоры (n, m) - бұл V кеңістігі мен n қосарланған V * кеңістігінің тензор көбейтіндісінің элементі (яғни V-дегі сызықтық функционалдар кеңістігі (ковекторлар))

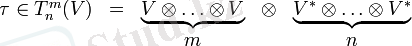
N + m сандарының қосындысы тензордың валенттілігі деп аталады (оны көбінесе дәреже деп те атайды). Деңгейдің тензоры (n, m) сонымен қатар n рет ковариантты және m ретке қарсы деп аталады.

NB көбінесе осы жерде анықталған валенттілік терминімен синоним ретінде ранг термині қолданылады. Керісінше де болады, яғни валенттілік терминін осы жерде анықталған дәреже мағынасында қолдану.

1.2. Тензор көп сызықты функция ретінде
Дәреженің (1,0) ковариантты тензоры сызықтық функционал ретінде ұсынылуы мүмкін сияқты, дәреженің тензоры rank (n, 0) n v векторлық аргументтің \ tau (v_1, v_2, \ ldots, v_n) функциясы ретінде қарастыру ыңғайлы v_i \ in V, ол әр аргументте сызықтық болып табылады (мұндай функциялар көп сызықты деп аталады), яғни F өрісінен кез-келген тұрақты с үшін (векторлық кеңістік анықталған)

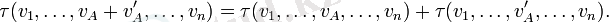
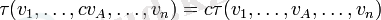
Сол венада тензор τ ерікті дәрежелі ранг (n, m) n векторлар мен m ковекторларының көп сызықты функционалымен ұсынылған:

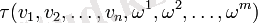
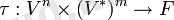
Біз V кеңістігінде негізді таңдаймыз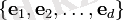және сәйкесіншежұптасқан кеңістіктегі дуальды негіз V * (яғни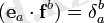онда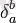Кронеккер символы).
Содан кейін, тензор кеңістігінде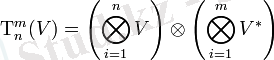табиғи түрде негіз пайда болады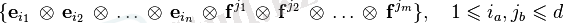Еркін тензор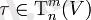негізгі тензор өнімдерінің сызықтық комбинациясы түрінде жазылуы мүмкін:

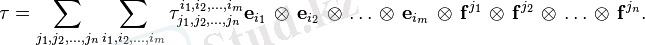
Эйнштейн конвенциясын қолдана отырып, бұл кеңейту келесі түрде жазылады

Сандар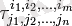тензор τ компоненттері деп аталады. Тензор компоненттерінің индекстері ковариант деп, ал жоғарғы сценарийлері контрравиант деп аталады. Мысалы, екі еселенген ковариантты тензордың h кеңеюі келесідей болады:

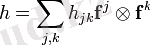
Егер сіз тензорды көп сызықты функция ретінде анықтасаңыз, онда оның компоненттері осы функцияның негіздегі мәндерімен анықталады

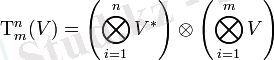
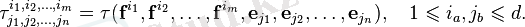
2.Тензор компоненттері

2.1. Классикалық анықтама туралы

Физика әдебиеттерінде жиі кездесетін тензорды анықтаудың классикалық тәсілі компоненттерде тензорларды ұсынудан басталады. Тензор геометриялық объект ретінде анықталады, ол көп өлшемді массивпен сипатталады, яғни бірнеше индекстермен нөмірленген сандар жиынтығы немесе басқаша айтқанда кесте (жалпы айтқанда n өлшемді, мұндағы n - тензор валенттілігі (жоғарыдан қараңыз)).

Сонымен, векторды (бірінші дәрежедегі тензор) бір өлшемді массив (жол немесе жақсырақ - баған), ал сызықтық оператор және квадраттық форма сияқты объектілерді екі өлшемді матрица анықтайды. Скаляр (нөлдік деңгей тензоры) бір санмен белгіленеді (оны бір элементті нөлдік өлшемді массив ретінде қарастыруға болады). (Скалярлар мен векторларды тензорлардың ерекше жағдайлары ретінде қарастырған ыңғайлы, өйткені олар үшін барлық тензор анықтамалары мен теоремалары жарамды және скаляры бар векторларды жалпы қарастыруда бөлек қалдыруға болады).

Матрицалық операцияларды (матрицаларды бір-бірімен және векторлармен көбейту), сондай-ақ нүктелік көбейтінді сияқты векторлық операцияларды тікелей жалпылау деп санауға болатын тензорлық операциялар енгізіледі. Бұл операциялар, егер біз қазіргі (аксиоматикалық) анықтамадан шығатын болсақ, онда матрицалық амалдар сызықтықтың сызықтығынан шығатындай, векторлық кеңістіктің негізінде тензорлармен ширатылған векторлар кеңейгеннен кейін, осы анықтамадағы тензорлардың (поли-) сызықтығынан тікелей шығады. операторлары және белгілі сызықты формалары, олардың әрқайсысы белгілі бір негізде белгілі бір матрица арқылы ұсынылған.

Бұл операциялар тензорларды векторлар мен скалярлар сияқты іргелі геометриялық объектілермен байланыстырады, нәтижесінде олардың геометриялық мағынасын анықтайды. Сол амалдар тензорларды координаталық трансформация матрицаларымен (Жакоби матрицалары) байланыстырады. Егер тензорлық анализ туралы айтатын болсақ (әдетте классикалық тәсілмен, кем дегенде, бірінші сатыда қарастырылатын Риман немесе псевдо-Риманн) жалпы формадағы коллекторда, бұл операциялар әдетте жалпы ковариантты түрде анықталады (яғни қисық сызықты таңдауға тәуелді емес әдіс) координаттар) метрикалық тензорды қолдана отырып.

Негізгі тензорлық амалдар қосу болып табылады, бұл тәсілде векторларға ұқсас компоненттік қосылуға дейін азаяды, ал векторлармен, өздерімен және өздерімен, матрицалық көбейтуді жалпылау, векторлардың скаляр көбейтіндісі және матрицаның ізін алу. Тензорды санға (скалярға) көбейту, қаласаңыз, конволюцияның ерекше жағдайы деп санауға болады, ол компоненттік көбейтуге дейін азаяды.

Массивтегі сандардың немесе тензор компоненттерінің мәндері координаттар жүйесіне тәуелді, бірақ тензордың өзі, геометриялық бірлік ретінде, оларға тәуелді емес. Бұл геометриялық мәннің көрінісін көп нәрсе деп түсінуге болады: әртүрлі скалярлық инварианттар, индекстердің симметриясы антисимметриясы, тензорлар арасындағы қатынастар және т.б. Мысалы, осьтерді айналдырғанда нүктелік көбейту және векторлық ұзындық өзгермейді, ал метрикалық тензор әрқашан симметриялы болып қалады. Кез келген тензорлардың өздерімен және немесе басқа тензорлармен (векторларды қосқанда), егер нәтижесінде индекс қалмаған болса, скалярлар, яғни координаталардың өзгеруіне қатысты инварианттар: бұл скаляр инварианттарды құрудың жалпы тәсілі.

Координаттар жүйесін өзгерткен кезде тензор компоненттері белгілі сызықтық заңға сәйкес түрленеді.

Тензордың бір координат жүйесіндегі компоненттерін біле отырып, егер сіз координатаны түрлендіру матрицасы көрсетілген болса, оның компоненттерін әрқашан басқасында есептей аласыз. Сонымен, екінші тәсілді формула ретінде қорытындылауға болады:

тензор = компонент массиві + негізді ауыстыру кезінде компонентті түрлендіру Заңы

Айта кету керек, бұл барлық тензорлар (бір векторлық кеңістіктегі барлық тензорлар), олардың дәрежесіне қарамастан (яғни, векторлар) бірдей координаталық түрлендіру матрицасы арқылы өзгертіледі (және егер бар болса, оның дуалы) суперкрипттер мен жазылымдар). Тензор компоненттері векторлардың тензор көбейтіндісінің сәйкес компоненттері сияқты заңға сәйкес өзгертіледі (тензор валенттілігіне тең мөлшерде), компоненттердің ковариациясы-қарама-қайшылықты ескереді.

Мысалы, тензор компоненттері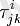үш вектордың тензор көбейтіндісінің компоненттерімен, яғни осы векторлардың компоненттерінің көбейтіндісімен бірдей өзгереді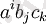Векторлық компоненттердің трансформациясы белгілі болғандықтан, тензордың классикалық анықтамасының қарапайым нұсқасын оңай тұжырымдауға болады.

3. Мысалдар
Тензор дәрежесі (0,0) - скаляр;
Бір рет қарама -- қарсы тензор (дәреже (0,1)) - бұл V кеңістігінің элементі, яғни вектор;
Тензор дәрежесі (1,0) - ковектор (ковариант векторы), яғни V кеңістігінің элементі * ;
Тензор дәрежесі (2,0) - бұл тангенс кеңістігіндегі gij метрикалық тензор сияқты билинарлық форма.
Тензор дәрежесі (1,1) желілік оператор болып табыладыАтап айтқанда, сәйкестендіру матрицасы арқылы ұсынылатын сәйкестендіру операторы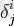Дәреже (1,1) энзор.

N өлшемді сызықтық кеңістіктегі көлем формасы дәреженің антисимметриялық тензорының мысалы болып табылады (n, 0) (немесе n рет ковариантты)
Табиғи формадағы риманналық қисықтық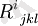ранг тензорының мысалы (3,1), оның конволюциясы - Ricci тензорыRij және скалярлық қисықтық R = Rijgij сәйкесінше (2,0) және (0,0) дәрежелі тензорлардың мысалдары болып табылады - яғни соңғысы скаляр болып табылады. Анықтамадан шығатын болсақ, тензор компоненттері координаттарды түрлендіру кезінде белгілі бір жолмен ол анықталған кеңістік векторларының компоненттерімен синхронды түрде өзгеруі керек. Демек, тензордың көрінісіне ұқсайтын индекстері бар кез-келген кесте немесе мөлшер тензорды білдірмейді.

Тензорды көрсетпейтін мұндай планшеттің қарапайым, біршама жасанды болса да мысалы, компоненттері координаталардың түрлендірулерінде кез келген жолмен өзгермейтін кез-келген сандар жиынын білдіретін планшет болуы мүмкін. Мұндай объект тензорды білдірмейді немесе кез келген жағдайда координаталық түрлендіру жүргізілген сызықтық кеңістіктегі тензорды білдірмейді. Сонымен, үш санның жиыны үш өлшемді векторды білдірмейді, егер бұл сандар координаталар өте нақты түрде өзгерген кезде өзгермесе.

Сондай-ақ, жалпы жағдайда, жоғары деңгейлі тензор құрамдас бөліктерінің жиынтығы төменгі деңгей тензоры емес.

Кем дегенде бір нонерентті емес координаталар жүйесінде барлық компоненттері нөлге тең объект, (ал толық негізде), ал қалған компоненттерде кем дегенде бір компонент нөлге тең емес, сонымен қатар тензорды білдірмейді. Бұл факт тензорлардың (поли-) сызықтығының салдары болып табылады.

Тек тензорға ұқсамайтын, бірақ олар үшін тензорлық операциялар анықталған (және ақылға қонымды және дұрыс мағынасы бар) объектілер бар (басқа тензорлармен, атап айтқанда, векторлармен конволюция), бірақ олар тензор емес:

Біріншіден, тензорларға координаталық түрлендірудің матрицалары (Жакоби матрицалары) кірмейді, бұл екі коллектор арасындағы диффеоморфизмнің ерекше жағдайы, олардың көмегімен тензордың классикалық анықтамасы енгізілген, бірақ олардың көптеген қасиеттері бойынша олар тензорға ұқсайды. Сондай-ақ, олар үшін сіз жоғарғы және жазылымдарды, көбейту, қосу және айналдыру амалдарын енгізе аласыз. Бірақ тензордан айырмашылығы, оның компоненттері тек берілген коллектордағы координаталарға тәуелді, Якоби матрицасының компоненттері кескін коллекторындағы координаталарға да тәуелді. Бұл айырмашылық екі ерікті коллектордың диффеоморфизмінің якоби матрицалары қарастырылған жағдайда айқын көрінеді; алайда коллекторды өз-өзіне бейнелегенде, оны елемеуге болады, өйткені кескіннің жанама кеңістіктері және кері кескін изоморфты (канондық емес). Соған қарамастан, ол сақталады. Якоби матрицалары мен тензорлары арасындағы ұқсастықты тек жанама және котангенсті емес, сонымен қатар коллектор мен олардың туындыларының үстіндегі ерікті векторлық шоғырларды қарастырсақ, дамытуға болады. Christoffel рәміздері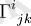сонымен қатар тензорды білдірмейді, егер оларды ерікті нүктенің жанындағы координаттарды таңдау арқылы нөлге теңестіруге болады, дәл сол сияқты (қисық сызықты) координаттарды нөлге айналдыруға болады. Алайда, вектормен қосылған компоненттердің конволюциясы нақты векторды береді, ал олардың айырмашылығы нақты тензор (бұралу тензоры) болады. Christoffel таңбалары, кез-келген байламдағы байланыс коэффициенттері сияқты, тензорлар кеңістігіне қарағанда күрделі кеңістіктің элементтері болып табылады.

4. Тензорлық операциялар

Тензорлар келесі алгебралық операцияларға мүмкіндік береді:
Скалярға көбейту - вектор немесе скаляр сияқты (тензордың ерекше жағдайлары);

Бірдей валенттілігі мен индекстерінің құрамындағы тензорларды қосу (векторлар сияқты қосындысын компонент бойынша есептеуге болады);

Скалярға көбейтудің және тензорларды ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.