Көпбұрыштардың ауданын оқыту әдістемесі


М. Мәметова атындағы Қызылорда педагогикалық жоғары колледжі
«Физика - математика және ақпараттық жүйе» бөлімі
«Қорғауға жіберілді»
ПЦК төрайымы
Жұмағұлова Г.
КУРСТЫҚ ЖҰМЫС
Тақырыбы: «Көпбұрыш фигурасынын ауданын окыту әдістемесі»
Пән: Математика оқыту әдістемесі
Мамандығы: 0111000 - «Негізгі орта білім»
Біліктілігі: 03 - «Ағылшынша білімі бар математика пәні мұғалімі»
Тобы: М - Л - 16
Орындаған: Бекмаш Мейіржан
Ғылыми жетекшісі: Суханбердина Ғазиза
Баға:
Қорғалған күні: «__»ж
Қызылорда қаласы 2020 ж.
МАЗМҰНЫ
К і р і с п е
Аудан - қарапайым шамалардың, соның ішінде геометриялық шамалардың мысалы болып табылады. Олай болса, аудан жайында түсінік қалыптастыру шамаларды қарастырудың, бағдарламаның түсініктеме бөлігінде келтіргендей жалпы әдістемесіне сәйкес жүргізіледі. Алдымен, әрине, «ауданға ие болу қасиетінің» қандай да бір затқа, яғни нәрсеге тән екенін, яғни аудан - заттың қасиетін сипаттайтынын түсіндірген жөн. Әр түрлі заттарды үстелге қойып, олардың әрқайсысының үстел бетінің біраз жерін (мөлшерін) алып тұрғанын көрсетуге болады. Ендеше әр заттың сәйкес бетінің ауданы бар. Көрнекі құралдарды пайдаланып, көз мөлшермен және беттестіру әдісімен заттардың аудандары бірдей немесе аудандары әртүрлі болатынын көрсетуге болады. Демек, екі ауданды бір-бірімен салыстыру барысында «тең», «артық», «кем» қатынастарының бірі тура болатынына көз жеткізіледі. Жазық фигураларды беттестіру кезінде олардың аудандары әртүрлі болса, бірінің ішіне бірі толық сыйып тұрады, ал аудандары бірдей болса, онда екеуі дәлме-дәл келеді. Егер екі фигураны бір-бірімен беттестіру мүмкін болмаса, онда олардың аудандарын салыстыру үшін басқадай тәсіл қолдануға тура келеді. Мәселен, «көз мөлшермен» салыстыруға болар еді, алайда бұл тәсілдің дәлірек нәтиже беруі әрдайым ықтимал бола қоймайды. Сондықтан әр фигураның ауданын оларды құрастырып тұрған бірдей шаршылар санын есептеу арқылы тауып анықтауға болады. Бұл тәсіл көп жағдайларда дәл және дұрыс нәтиже беруі мүмкін. Демек, бұрынна қарастырылып келген шаршылардан (бөліктерден) фигура құрастыру және оған керісінше, фигураны шаршыларға (бөліктерге) бөлу сияқты жаттығуларды орындау барысында фигураның ауданы жайында түсінік қалыптастыру, сондай-ақ фигуралар аудандарын салыстыруға машықтандыру жүзеге асырылады.
Ауданның өлшем бірлігімен таныстыру ұзындықтың сәйкес бірлігін енгізуге ұқсас және онымен байланысты қарастырылады. Айталық, ұзындықтың бірлігі ретінде ұзындығы 1 см кесінді алынса, ауданның бірлігі ретінде қабырғасы 1 см шаршының ауданы (1см 2 ) алынады. Сантиметрдің көмегімен кесіндінің ұзындығын өлшеу 1 см бірлік кесіндінің берілген кесіндіге біртіндеп неше рет салынғанын анықтау болса, фигураның ауданын табу 1 см 2 неше шаршыдан құрастырылғанын анықтау.
Квадрат сантиметрдің көмегімен кез-келген жазық фигураның, соның ішінде көпбұрыштың ауданын табуға болады. Ол үшін палетканы пайдаланады. Палетка - квадрат сантиметрлерге бөлінген мөлдір пластина. Онымен фигураны жауып қойып, фигура контурымен шектелген толық квадрат сантиметрлерді санайды, оған барлық фигура контурына сыйып тұрған толық емес квадрат сантметрлер санының жартысын қосады. Осы тәсілмен кез-келген көпбұрыштың ауданын есептеп табуға болады. Осыған машықтандыру мақсатында әр оқушы полиэтилен параққа палетканың үлгісін жасап алғаны жөн, оның өлшемдері 10 см*10 см. Ол палетканы көбейту кестесін құру кезінде көрнекі құрал ретінде пайдалануға да болады.
Көпбұрыштың ауданын табу тәсілін қарастырғанда осындай көпбұрыштың мысалы ретінде тік төртбұрыш (шаршы) алынады. Алайда оның ауданын табуға қатысты тұжырымдаманы дайын күйінде бірден бермей, ол қорытындыға оқушылар біртіндеп келгені жөн. Оны мына ретпен ұсынылатын жаттығулар арқылы жүзеге асыруға болады: бірнеше қатарға және бағанға бөлінген, бірдей шаршылардан құрастырылған тік төртбұрыштың ауданын, осы шаршылар санын әр түрлі тәсілмен есептеу арқылы анықтау; тік төртбұрышты (шаршыны) бағандарға бөлудің үлгісі көрсетіледі; бір баған неше шаршыдан құрастырылғаны нақты көрсетіледі, сондай-ақ барлығы неше баған шығарып алуға болатыны қабырғаларындағы бөліктерге орай анықталады; тік төртбұрыштың қабырғалары сантиметрлік бөліктерге бөлініп көсретілген, соны пайдаланып неше қатар, неше баған квадрат сантиметр шығарып алуға болатыны анықталады; тік төртбұрыштың қабырғаларының ұзындықтары сантиметрмен беріледі; соларды пайдаланып неше баған және неше қатар квадрат сантиметрлер шығарып алуға болатыны анықталады.
Осыларды біртіндер қарастыру нәтижесінде тік бұрыштың ауданын табу үшін оның бірдей бірлікпен алынған ұзындығы мен енін көбейтк еректігі тұжырымдалады.
Зерттеу мақсаты:
- Оқушылардың көпбұрыштың фигураның аудынын табуда ойлауын қалып-тастыру.
Зерттеу жұмысының міндеттері:
- Оқушыларға көпбұрыш, ұғымдарын игеруге көмектесу;
- Көпбұрыштардың ауданы негізгі есептерін шығару;
- Оқушыларға көпбұрыш негізін үйрету.
Зерттеу пәні: Көпбұрыштың ауданын табу
Зерттеудің ғылыми болжамы: Егер жалпы білім беретін мектептің оқыту процесінде оқушыға сабақ түсіндіруге көпбұрыштардың ауданын табу қолданса, онда оқушылардың білім сапасын арттырып, пәнге деген қызығушылығын қалыптастыруға мүмкіндік туғызар едік.
Зерттеу әдістері: Зерттеу тақырыбы бойынша математикалық әдебиеттерге талдау жасау, математикалық басылымдар мен нормативтік құжаттарды, зерделеу, жинақтау, салыстырмалы талдау, тәжірибелік эксперименттік жұмысын жүргізу, сауалнама алу, оның нәтижесін қорытындылау әдістері.
СызықСызық - геометриялық ұғым. Сызықтың әзірше мүмкін жағдайлардың бәрін қамтитын анықтамасы жоқ және ол геометрияның әр түрлі саласында түрліше тұрғыдан қарастырылады.
1) Элементар геометрияда түзу сызық, түзуден бөлінген кесінділер, кесінділерден құралған сынық сызық және кейбір қисық сызық қарастырылады. Әрбір сызық арнайы тәсілдермен анықталады (мысалы, шеңбер D орталығынен бірдей қашықтықта жатқан барлық нүктелердің жиынтығы арқылы анықталады) .
- Түзу сызықкөбіне анықтамасыз қабылданады.
- Сынық сызықкесінділерді бір-біріне ұштастыру арқылы құрастырылады.
- Қисық сызықтыңең қарапайым түрі - шеңбер. Беттің кез келген бөлігінің шекаралары, сондай-ақ қозғалыстағы нүктелердің траекториясы да сызық болып есептеледі.
2) Нүктенің траекториясы ретінде қарастырылатын сызықты параметрлік теңдеулер арқылы сипаттауға болады. Мысалы, жазықтықтағы тік бұрышты (х, у) координаттар жүйесінде радиусы R болатын, орталығы координаттар басында орналасқан шеңберді x = Rcost, y = Rsіnt теңдеулері арқылы енгізуге болады. Мұндағы t параметрі 0 ≤ t ≤ 2 кесіндісіндегі мәндерді қабылдаса, онда М(х, у) нүктесінің траекториясы шеңбер болады. Жалпы алғанда жазықтықтағы cызық x = ƒ(t), y = ƒ(t) теңдеулерімен, ал үш өлшемді кеңістіктегі cызық x = ƒ(t), y = ƒ(t), z = ƒ(t) түріндегі теңдеулерімен өрнектеледі. Бұл жерде t параметрі сан осінің шектеулі немесе шектеусіз аралығындағы мәндерді қабылдайды. ƒ(t), ƒ(t), ƒ(t) - осы аралықтағы үздіксіз функциялар.
3) Аналитикалық геометрияда жазықтықтағы сызық Ғ(х, у) = 0 теңдеуімен, ал үш өлшемді кеңістіктегі сызық Ғ 1 (х, у, z) = 0, Ғ 2 (х, у, z) = 0 теңдеулер жүйесімен беріледі. Егер Ғ(х, у) функциясы n=1 дәрежелі көпмүшелік болса, Ғ(х, у) = 0 теңдеуімен анықталатын сызық алгебралық қисық сызық деп аталады. n саны алгебрfks0 қисық сызықтың реті.
- Түзу - бірінші ретті сызық.
- Шеңбер, эллипс, гипербола, парабола - екінші ретті сызықтар, олар(х-у) 2= 0теңдеуімен анықталады.
- Үшінші (Декарт жапырағы, кубтық парабола, жартылай кубтық парабола т. б. )
- Tөртінші (Бернулли лемнискатасы, Декарт овалдары, кардиоида, т. б. ) және одан да жоғары (Лама қисығы, синусоидалық спираль) ретті сызықтардың жиі кездесетін түрлері.
Алгебралық қисықтардан өзгеше сызықтар трансцендент сызықтар (тригонометриялық, көрсеткіштік, логарифмдік, гиперболалық функциялардың графиктері, квадратриса, трактриса, т. б. ) деп аталады. Сызылу әдісі жағынан біріне-бірі жақын бір топ сызық циклоидалық қисық сызықтар (астроида, гипоциклоидалар, эпициклоидалар, т. б. ) деп аталады. Циклоидалық сызықтардың кейбіреулері алгебралық қисық сызықтарға, кейбіреулері трансцендент қисықсызықтарға жатады. Үшінші ретті сызықтардың 76 түрі (И. Ньютон), төртінші ретті сызықтардың 146 түрі (Л. Эйлер) бар.
4) Проективтік геометрияда жазықтықтағы алгебралық сызық біртектес координаталар арқылы Ғ(х1, х2, х3) = 0 теңдеуімен берілуі мүмкін.
5) XIX ғасырдың 80-жылдарында француз математигі К. Жорданның ұсынуы бойынша кез келген шағын аймақтағы байланысқан континуум (мысалы, үшбұрыш, төртбұрыш, куб, т. б. ) кесіндінің үздіксіз бейнесі бола алады. Кесіндінің бірмәнді үздіксіз бейнесін қарапайым доға немесе жордан доғасы деп, ал шеңбердің бірмәнді үздіксіз бейнесін қарапайым тұйық сызық деп атайды. Қазіргі топологияда сызық ұғымының 1921 ж. кеңес математигі П. С. Урысон ұсынған анықтамасы қолданылады. Оның айтуы бойынша сызық - өлшемділігі 1-ге тең еркін алынатын континуум.
6) Екінші ретті сызықтарды ежелгі заманның математиктері зерттей отырып, бірқатар жоғары ретті алгебралық қисықтарды және транцендент сызықтарды қарастырды. Алайда сызықтарды зерттеу және оларды кластарға бөлу аналитикалық геометрия қалыптасқаннан кейін ғана басталды.
Көпбұрыш
Көпбұрыш - жазықтықтағы кез келген тұйық сынық сызық. Сынық сызықтың әрбір бөлігі көпбұрыштың қабырғасы, ал олардың ұштары көпбұрыштың төбелері деп аталады. Егер сынық сызық қарапайым болса, онда көпбұрыш қарапайым көпбұрыш деп, ал күрделі болса, жұлдыз тәрізді көпбұрыш деп аталады. Көпбұрыш жазықтықты бірнеше облысқа бөледі. Қарапайым көпбұрыш жазықтықты біреуінде түзу толығынан жататын, ал екіншісінде толық жатпайтын екі облысқа бөледі. Біріншісін көпбұрыштың сыртқы облысы, екіншісін ішкі облысы дейді. Көпбұрыш осы облыстардың шекарасы болады. Көпбұрыш пен оның ішкі облысын біріктірсек, екі өлшемді көпбұрыш шығады. Егер көпбұрыштың төбелері кез келген қабырғасы арқылы жүргізілген түзудің бір жағында жатса, онда оны дөңес көпбұрыш дейді. Төбесі арқылы өтетін қабырғалардың ішкі облыс жағынан жасайтын бұрышын көпбұрыштың ішкі бұрышы дейді.
Кез келген n қабырғалы өзара қиылыспайтын көпбұрыштың ішкі бұрыштарының қосындысы (n-2) 8180°-қа тең. Әрбір қарапайым көпбұрыштың кем дегенде бір бұрышы жазық бұрыштан кіші болады. Бір қабырғаның ұштары болмайтын екі төбені қосатын кесіндіні көпбұрыштың диагоналы дейді. Егер көпбұрыштың барлық қабырғалары мен ішкі бұрыштары өзара тең болса, онда оны
дұрыс көпбұрыш
деп атайды. Дұрыс көпбұрыш әрқашанда дөңес болады. Тек үшбұрыштың ғана қабырғаларының теңдігінен бұрыштарының теңдігі шығады. Жалпы жағдайда олай болмайды. Қабырғалары тең, бірақ бұрыштары әр түрлі n бұрышты көпбұрыш (n>3) және бұрыштары тең, бірақ қабырғалары әр түрлі n бұрышты көпбұрыш болуы мүмкін. Дұрыс көпбұрыштың барлық төбелері арқылы өтетін сырттай шеңбер сызуға болады. 1801 ж. неміс математигі Карл Гаусс циркульдің және сызғыштың көмегімен қабырғалары m = 2n8p18p28 . . . 8pk түрінде берілген (мұндағы p
1
, p
2
, . . . , p
k
- әр түрлі гаусстық жай сандар) дұрыс көпбұрышты салуға болатындығын көрсетті. Қазіргі кезде гаусстық санның (p) мынадай 5 түрі белгілі: 3, 5, 17, 257, 65337. Зерттеу жұмыстарының нәтижесінде m = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 32, 34, . . . болғанда көпбұрышты салуға болатындығы, ал m = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33, . . . болғанда көпбұрышты салуға болмайтындығы анықталды. Бесбұрыштан бастап дөңес емес дұрыс көпбұрыш (өзара қиылысатын немесе жұлдызшалы) кездеседі. Олардың барлық қабырғалары тең, барлығының бұрыштары тең және бағыттары бірдей болады. Мұндай көпбұрыштардың төбелері бір шеңбердің бойында жатады. [1]
Төмендегі кестеде дұрыс көпбұрыштар қабырғаларының саны және оларды сырттай және іштей сызылған шеңберлерді радиустарының ұзындығын, көпбұрыштардың аудандарын анықтайтын формулалар топталған.
Дұрыс көпбұрыштың қабырғасының ұзындығы - k
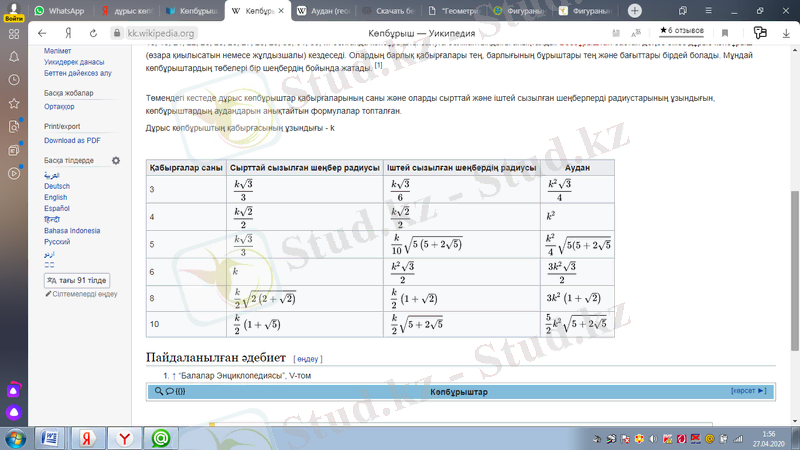
Дұрыс көпбұрыштар дегеніміз барлық қабырғалары және іргелес жатқан қабырғалар арасындағы бұрыштары тең фигуралар.
Мысалы тең қабырғалы үшбұрыш дұрыс көпбұрыш болады:
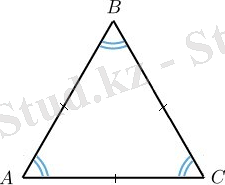
Осы үшбұрыштың барлық қабырғалары және іргелес жатқан қабырғалар арасындағы бұрыштар тең болады.
Басқа дұрыс көпбұрыштар мысалдары:
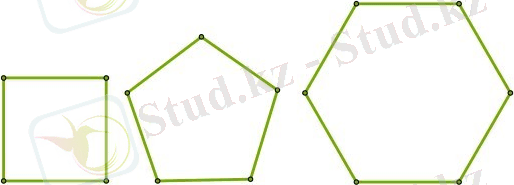
Дұрыс көпбұрыштың іргелес жатқан қабырғаларының арасындағы бұрыш мына формула арқылы аңықталады:
a = 180*(n-2) /n
Мысалы дұрыс үшбұрыш үшін n=3, a = 180*(3-2) /3 = 60 0
Ал квадрат үшін n=4, a = 180*(4-2) /4 = 90 0 .
Жаттығу ретінде дұрыс бесбұрыштың бір бұрышын және бұрыштардың жалпы соммасын есептеңіз.
Жазық фигуралардың ауданы ұғымыКесіндінің ұзындығы дегеніміз белгілі бір масштабтық кесіндімен салыстарғандағы осы кесіндінің өлшемі. Жазық фигура ауданы дегеніміз де осы сияқты ұғым.
Жазық фигуралардың ауданы ұғымының кесінді ұзындығы ұғымынан ерекшелігі: Екі кесіндінің ұзындықтары тең болса, онда бұл кесінділер тең болады; екі бұрыштың градустық (немесе радиандық) өлшемдері тең болса, онда бұл бұрыштар да тең болады, ал бұл нәрселер фигуралардың аудандарын өлшеу процесінде жүзеге аса бермейді. Яғни, әртүрлі, өзара ұқсас емес фигуралардың ауданы тең болуы мүмкін . Мұндай фигураларды тең шамалы фигуралар деп атайды.
Аксиомалар1. Тең фигуралардың аудандары да тең.
2. Егер фигура қандай да бір сызықпен екі басқа фигураларға бөлінсе, онда берілген фигураның ауданы осы бөліктердің аудандарының қосындысына тең.
3. Қабырғасы бір өлшем бірлігіне тең квадраттың ауданы 1-ге тең. Осы аксиомалардан мынадай салдар шығады.
Дұрыс көпбұрыштың түрлері:
Үшбұрыштың ауданы
Үшбұрыштың ауданы оның қабырғасы мен сол қабырғаға түсірілген биіктігі көбейтіндісінің жартысына тең. Яғни
S=1/2 · ah
формуласымен есептеледі, мұндағы a - үшбұрыштың қабырғасы, h - сол қабырғаға түсірілген биіктік.
Толықтама
Үшбұрыштың ауданын табудың басқа да формулалары бар:
Үшбұрыштың ауданы оның екі қабырғасы мен осы қабырғалар арасындағы бұрыштың синусы көбейтіндісінің жартысына тең. Яғни S=1/2 · ah sin γ формуласымен есептеледі, γ - олардың арасындағы бұрыш.
Келесі формула Ӏ ғасырда Александрия қаласында өмір сүрген ертедегі грек ғалымы Геронның атымен аталады. Егер үш қабырғасы белгілі болса, үшбұрыштың ауданын Герон формуласымен есептеуге болады:
S=√p(p-a) (p-b) (p-c)
мұндағы a, b, c - үшбұрыштың қабырғалары, ал p - оның жарты преиметрі яғни: p=a+b+c/2
Тікбұрышты үшбұрыштың ауданы және периметрі
Тікбұрышты үшбұрыш бір-біріне перпендикуляр тік бұрышты екі аяғымен және гипотенуспен - ең ұзын жағынан жасалған.
Үшбұрыштағы бұрыштардың сомасы 180° құрайды, бұл α + β = 90°.
Үшбұрыштың жағының ұзындығы тригонометриялық функциялар арқылы Пифагор теоремасы және бұрыш өлшемдері арқылы анықталуы мүмкін.
Формулалар
P - периметр
S - ауданы
a, b - тікбұрышты бұрыштың аяқтары да тікбұрышты болады
c - гипотенуса
Тең бүйірлі үшбұрышТеңбүйірлі үшбұрыш - бұл ұзындықтары бойынша екі қабырғасы тең үшбұрыш. Бүйір қабырғалары деп тең қабырғаларын, ал соңғысын - табаны деп атайды. Анықтамасы бойынша дұрыс үшбұрыш теңбүйірлі болып табылады, алайда кері пікір дұрыс емес, яғни теңбүйірлі үшбұрыш дұрыс үшбұрыш бола алмайды.
Қасиеттері- Теңбүйірлі үшбұрыштың тең қабырғаларына қарама-қарсы жатқан бұрыштар өзара тең. Сондай-ақ осы бұрыштардан түсірілген биссектрисалар, медианалар мен биіктіктері тең болады.
- Теңбүйірлі үшбұрыштың табанына жүргізілген биссектриса, медиана, биіктік пен орта перпендикуляр өзара тең болады. Іштей және сырттай сызылған шеңбердің центрі осы түзулердің бойында жатады.
a - теңбүйірлі үшбұрыштың екі тең қабырғасы, b - үшінші қабырғасы, h - теңбүйірлі үшбұрыштың биіктігі, α мен β - сәйкес бұрыштар, R - сырттай сызылған шеңбердің, ал r - іштей сызылған шеңбердің радиусы болсын.
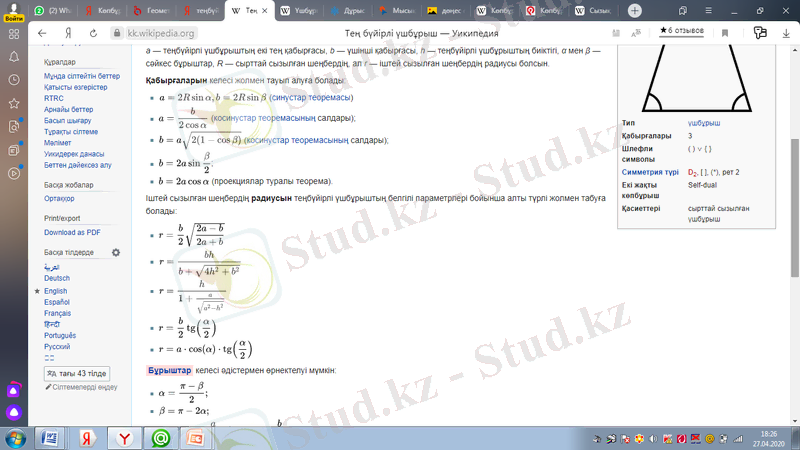
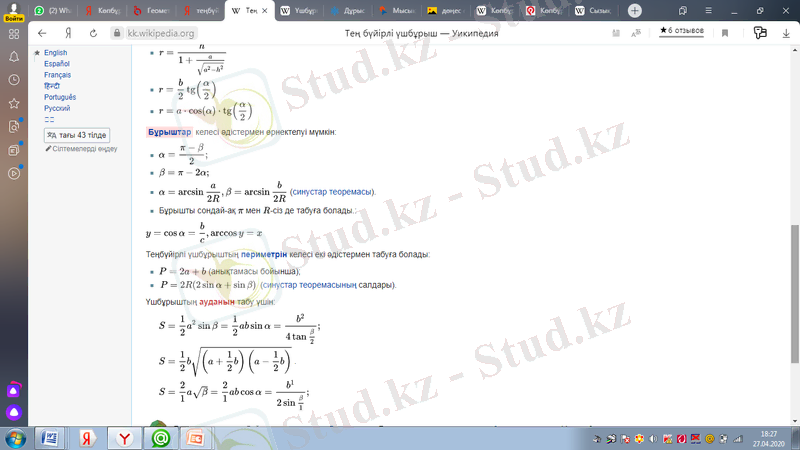
Төртбұрыш - төрт нүктеден және оларды тізбектей қосатын төрт кесіндіден тұратын фигура.
Сонда бұл берілген нүктелердін ешбір үшеуі бір түзудің бойында жатпауы тиіс, ал оларды қосатын кесінділер қиылыспайтын болуы тиіс. берілген нүктелер төрбұрыштың төбелері деп, ал оларды қосатын кесінділер төртбұрыштың қабырғалары деп аталады. [
S=ab
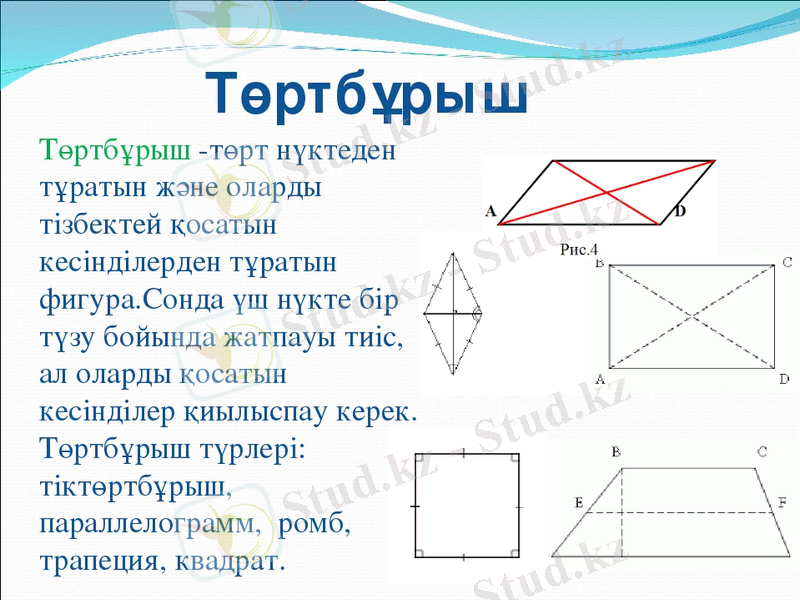
Трапеция - деп тек қарама - қарсы екі қабырғасы параллель, ал қалған екі қарама - қарсы қабырғалары қиылысатын төртбұрышты айтады.
Параллель қабырғалары трапецияның табандары деп аталады, басқа екі қабырғасы бүйір қабырғалары деп аталады, ал бүйір қабырғаларының орталарын қосатын кесіндіні трапецияның орта сызығы деп атайды.
Трапецияның қасиеттері
- Трапецияның орта сызығы оның табандарына параллель және сол табандардың қосындысының жартысына тең болады.
- Егер трапеция тең бүйірлі болса онда оның диагональдары және табанындағы бұрыштары тең болады.
- Егер трапеция тең бүйірлі болса, онда оған сырттай шеңбер сызуға болады.
- (3-ке кері. ) Егер трапецияға сырттай шеңбер сызуға болатын болса, онда ол тең бүйірлі. [1]
ПараллелограммТрапецияның ауданы:
Параллелограмм - қарама-қарсы қабырғалары параллель болатын, яғни параллель түзулердің бойында орналасқан төртбұрыш.
Параллелограммның қасиеттері- Қарама - қарсы орналасқан қабырғалары тең. : {\displaystyle AB=CD}, {\displaystyle AD=BC}.
- Қарсы жатқан бұрыштары тең. : {\displaystyle \angle A=\angle C, \angle B=\angle D. }
- Диагональдары қиылысады және қиылысу нүктесінде қақ бөлінеді. : {\displaystyle AO=OC}, {\displaystyle BO=OD}.
- Бұрыштарының іргелес біржақты жатқан қабырғаларының қосындысы 180º-қа тең.
- Диагональдарының квадраттарының қосындысы оның барлық қабырғаларының квадраттарының қосындысына тең.
{\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}) . }Параллелограммның белгілері
Егер мына шарттар орындалса онда төртбұрыш параллелограмм болады:
- Қарама - қарсы қабырғалары тең және параллель (AB = CD, AD = BC)
- Қарама - қарсы қабырғалары қос - қостан тең (AB = CD, AB CD) .
- Қарама - қарсы бұрыштары қос - қостан тең (∠A = ∠C, ∠B = ∠D) .
- Диагональдары қиылысу нүктесінде қақ бөлінеді (AO = OC, BO = OD) . [1]
Параллелограммның ауданы: S=ah
Ромб
Ромб (гр. ρομβος ) - Барлық қабырғалары тең болатын параллелограммды айтады.
Термин көне грек тіліндегі «дабыл» сөзімен сәйкес келеді. Егер бүгінде дабылдарды негізінен дөңгелек пішінде жасайтын болса, бұрын оларды квадрат не ромб түрінде жасаған. «Ромб» сөзін алғаш рет Герон мен Папп Александрийский қолданды.
Ромбтың қасиеттері
-Параллелограммның барлық қасиеттері.
-Дигоналдары перпендикуляр.
-Диагоналдары өздері шығатын бұрыштарының биссектрисалары болып табылады.
Ромбтың белгілері
-Параллелограмм ромб болады егер:
-Оның екі айқыш қабырғалары тең.
-Диагоналдары перпендикуляр.
-Диагоналдарының біреуі бұрышының биссектрисасы болса.
Ромбының ауданының формуласы: S=ah
Шаршы
Шаршы (Квадрат) - шаршы деп сыбайлас қабырғалары өзара тең тіктөртбұрышты айтады. Техникада Шаршы тәрізді тесіктері бар тетіктер көп кезігеді. [1]
Квадрат (лат. quadratus - төртбұрышты) - 1) барлық қабырғасы бірдей тік төртбұрыш; 2) бірдей екі көбейткіштің көбейтіндісі (а⋅а) немесе санның екінші дәрежесі (а2) ; 3) типографиялық өлшемнің 48 пункт ке (шамамен 18 мм ) тең бірлігі ( жолдың ұзындығы, терім форматы, шрифтінің өлшемі , т. б. ) ; 4) типографиялық терім материалы аралығының бір түрі (оның ені 48 пункт ке, қалыңдығы қаріптің кегліне тең) . [2] Аудан S=a*a
Тік төртбұрыш
Тік төртбұрыш - Барлық бұрыштары тік болып келетін параллелограммды тік төртбұрыш деп атайды.
Тіктөртбұрыштың қасиеттері
Барлық параллелограммның қасиеттеріне ие болады.
Диагональдары тең.
Ауданы бір-бірімен түйісетін екі жағының ұзындықтарының көбейтіндісіне тең болады. S=a. b
Тік төртбұрыштың белгілері
Параллелограмм тіктөртбұрыш болады егер:
Бұрыштарының біреуі тік болса.
Диагональдары тең болса. [1]
Бесбұрыштың ауданы және периметрі
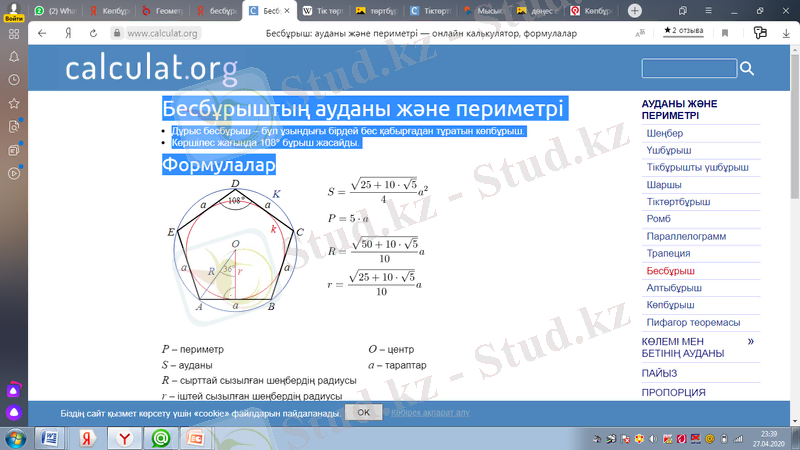
Дұрыс бесбұрыш - бұл ұзындығы бірдей бес қабырғадан тұратын көпбұрыш. Көршілес жағында 108° бұрыш жасайды.
Формулалар
Алтыбұрыштың ауданы және периметрі
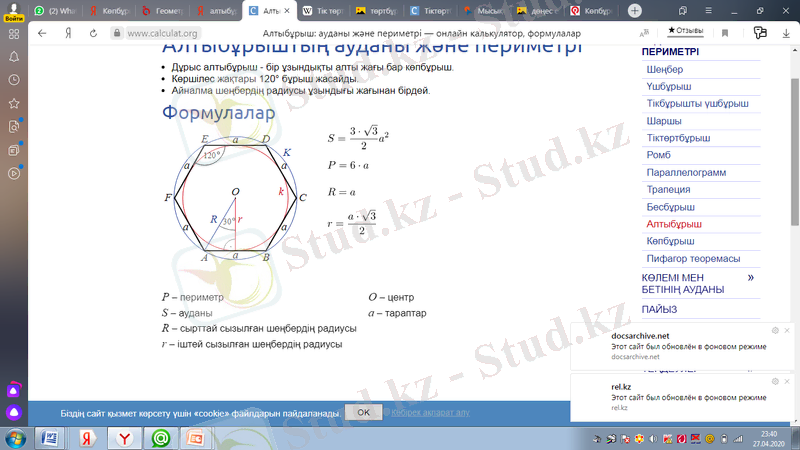
Дұрыс алтыбұрыш - бір ұзындықты алты жағы бар көпбұрыш.
Көршілес жақтары 120° бұрыш жасайды.
Айналма шеңбердің радиусы ұзындығы жағынан бірдей.
Шеңбер
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz