Адиабаталы жіктелген термодинамикалық жүйелер

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 93 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

СемЕЙ қаласының ШӘКӘРІМ атындағы МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІСемЕЙ қаласының ШӘКӘРІМ атындағы МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ: 3 деңгейлі СМК құжаты

ПОӘК

ПОӘК 042-18-38. 1. 64

/03-2014

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІСемЕЙ қаласының ШӘКӘРІМ атындағы МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ:

ПОӘК

«Статистикалық физика және физикалық кинетика негіздері» пәнінің оқу-әдістемелік материалдары

№2 басылым

25. 06. 2014ж.

ПӘННІҢ ОҚУ-ӘДІСТЕМЕЛІК КЕШЕНІ

«Статистикалық физика және физикалық кинетика негіздері»

« 5В011000 - Физика » мамандығы үшін

ОҚУ-ӘДІСТЕМЕЛІК МАТЕРИАЛДАРЫ

Семей

2014

Мазмұны

Глоссарий

1: 2

Глоссарий: Дәрістер

3: 5

1: 3

Глоссарий: Практикалық сабақтар

3: 73

1: 4

Глоссарий: Студенттердің өздік жұмыстары

3: 81

1 ГЛОССАРИЙ

азғындалған газ - температурасы азғындау температурасынан төмен болган жағдайдағы кванттық газ

бозе-газ - спиндері нөлге немесе бүтін санға тең. Бозе - Эйнштейн статистикасына бағынатын бөлшектерден тұратын кванттық газ

бозе-эйнштейн статистикасы - бозондардан тұратын жүйеге қолданылатын кванттық статистика

бозе-эйнштейн конденсациясы - азғындау температурасынан төмен температурада көптеген бозондар ең төмен энергияға ие болатын күйді толтыратын құбылыс. Кез келен басқа күйде бозондар саны аз болады

бозе-эйнштейн үлестірілуі - өзара әрекеттеспейтін энергиясы болатын күйде орналасатын бозондар санының орташа мәні

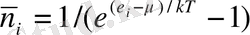мұндағы 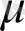- химиялық потенциал, k -Больцман тұрақтысы

бозон - нөлдік немесе бүтін спинге ие болатын бөлшек немесе квазибөлшек. Бозон Бозе-Эйнштейн статистикасына бағынады

Больцман статистикасы - классикалық механика заңдары бойынша қозғалатын, көп өзара әрекеттеспейтін бөлшектердің физикалық қасиеттерін статистикалық түрде сипаттау

борндық жуықтау - микробөлшектердің шашырау теориясындағы, бөлшектердің шашырау амплитудасын бірінші жуықтауда есептеу әдісі

Больцман үлестірілуі - идеал газ бөлшектерінің р импульстер және 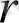координаталар бойынша тепе-тең үлестірілу функциясы

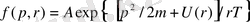
Больцманның кинетикалық теңдеуі - молекулалар өзара соқтығысуы нәтижесінде пайда болатын тепе-теңдікті сипаттайды

идеал газ - бөлшектредің өзара әрекеттесуі есептке алынбайтын газдың теориялық моделі

Гиббстің каноникалық үлестірілуі - ортамен жылулық тепе-теңдікте орналасқан және көлемі мен бөлшектер саны тұрақты жүйелердің статистикалық ансамблі күйлерінің ықттмалдықтарының үлестірілуі

кванттық статистика - көп бөлшектерден тұратын кванттық жүйелердің статистикалық физикасы

кинетикалық теңдеу - тепе-тең емес процестерді сипаттайды, ол үлестірілу функциясына арналған интегродифференциалды теңдеу

нақты газ - қасиеттері молекулалардан өзара әрекеттесуіне тәуелді газ

тепе-тең емес процестер - термодинамика және статфизикадағы тепе-тең емес күйлерді қамтитын физикалық процестер

тепе-тең емес күйлер - термодинамикадағы термодинамикалық тепе-теңдіктен, статфизикадағы статистикалық тепе-теңдіктен шығарылған жүйенің күйі

тасымалдау құбылысы - қайтымсыз процестер, олардың нәтижесінде физикалық жүйеде электр заряды, масса, импульс, энергия, энтропия және т. б. физикалық шамалар кеңістікте тасымалданады

тепе-тең күйлер - үлкен уақыт аралығында тұйықталған жүйенің тепе-тең күйге көшкен күйі. Бұл уақыт релаксация уақыты деп аталады

термодинамиканың бірінші бастамасы - жылулық құбылыстарға арналған энергияның сақталу заңы

Резерфорд формуласы - Кулон заңымен әрекеттесетін, релятивистік емес зарядталған нүктелік бөлшектердің шашырау қимасын анықтайды

релаксация - макроскопиялық физикалық жүйелерде тепе-теңдіктің пайда болу процесі

статистикалық салмақ - кванттық статистикадағы берілген энергияны кванттық күйлердің әр түрлі сандары. Статистикалық саламақ күй азғындауының еселігі деп те атайды

статистикалық механика - макроскопиялық денелердің қасиеттерін өте көптеген бөлшектерден (молекулалардан, атомдардан, электрондардан) тұратын жүйелер ретінде қарастыратын физиканың бөлімі. Статистикалық физикада ықтималдықтар теориясына негізделген статистикалық әдістер қолданылады

статистикалық қосынды - Z шама, ол 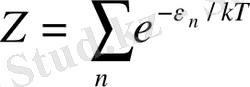, мұнда 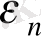- n кванттық күйдегі энергия үлестірілу функциясы - ол

статистикалық физика - макроскопиялық денелердің қасиеттерін өте көптеген бөлшектерден (молекулалардан, атомдардан, электрондардан) тұратын жүйелер ретінде қарастыратын физиканың бөлімі. Статистикалық физикада ықтималдықтар теориясына негізделген статистикалық әдістер қолданылады

статистикалық ансамбль - дегеніміз бір-біріне тең емес күйлерде орналасқан көп нақты жүйелердің қосындысы деп атауға болады

статистикалық термодинамика - физикалық жүйелердің тепетеңдік күйлерін сақта-ғандағы жалпы физикалық қасиеттерін зертейтін теоретикалық физиканың бөлімі. Термодинамика екі бөлімнен құралады феноменологиылық және статистикалық термодинамикадан. Феноменологиялық термодинамикада өтіп жатқан жүйелердегі процесстерді қарастырғанда молекулалрдың ішкі құрамдары және молекулярлық процесстерінің механизмдары есептелмейді. Термодинамика мен статискалық физика материяның жылулық қозғалыстарын зерттейді. Сондай теоретикалық зерттеуде заттарда өтіп жатқан физикалық процесстерді анықтау үшін көп модельдік ұғымдар пайдаланды

термодинамика - жылулық қозғалыстың заңдылықтарын және оның заттың физикалық қасиеттеріне тигізетін ықпалын энергетикалық тұрғыдан қарастыратын ғылым

термостат - тұрақты температураны ұстайтын прибор

термодинамиканың екінші бастамасы - өздігінен температурасы төмен денеден температурасы жоғары денеге жылудың ауыса алмауы

термодинамикалық жүйе - көп материалдық нүктелердің қосындысы деп саналады. Материалдық нүктелер ылғи хаотикалық қозғалысқа қатнасадыда, бір- бірімен кинетикалық энергиямен, жылдам-дықпен, импульспен алмасады, бірақ олардың ішкі күй жағдайы өзгерілмейді

термодинамиканың үшінші бастамасы - абсолют нөлге ұмтылғанда тепе-тең күйде дененің энтропиясының нөлге ұмтылуы

ферми-газ - жартылай бүтін санды спинге ие болатын бөлшектреден тұратын кванттық газ. Ферми-газ ретінде металдағы электрондық газды алуға болдаы

ферми-деңгей - Ферми энергиясына сәйкес, фермиондар жүйесінің кейбір шартты энрегия деңгейі

ферми-энергиясы - абсолют нөл температурада, өзінен төмен орналасқан барлық деңгейлер фермиондармен толтырылатын энергияның мәні

Ферми-Дирак үлестірілуі - өзара әрекеттестігін есепке алмауға болатын теңбе-тең фермиондардың энергетикалық деңгейлер бойынша үлестірілуін сипаттайтын өрнек. Бұл күйге сәйкес келетін осындай бөлшектердің орта саны Ферми-Дирак үлестірілуімен анықталады:

фермион - жартылай бүтін спинге ие болатын бөлшек немесе квазибөлшек. Фермиондарға электрон, протон, нейтрон, кварктар және т. б. жатады

флуктуация - көп бөлшектерден тұратын жүйені сипаттайтын физикалық шамалардың орта мәндерінен кездейсоқ ауытқулары

Ферми-Дирак статистикасы - теңбе-тең фермиондар жүйелеріне арналған кванттық статистика

ферми беті - квазиимпульстер кеңістігінде өткізгіштік электрондары бар облысты, Т=0К температурада электрондары жоқ облыстан бөлетін 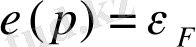изоэнергетикалық бет. Мұндағы - Ферми энергиясы

I ретті фазалық ауысу - ауысу жылуы бөлінетін және көлем секірмелі түрде өзгеретін ауысу

II ретті фазалық ауысу - бұл жағдайда ауысу жылуы болмайды және көлем секірмелі түрде өзгермейді

үлестірілу функциясы - ол - нормалау шартын қанағаттандырады:

үлкен каноникалық үлестірілу - 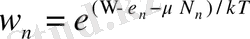мұнда 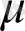- химиялық потенциал, - бөлшектер саны, - нормалау шартынан табылады

физика - материяның жалпы формалары және өзара түрленуі туралы ғылым, ол дәл ғылымдарға жатады және айналамыздағы процестермен құбылыстардың сандық заңдылықтарын зерттейді

физикалық заңдар - табиғатта болатын тұрақты қайталанатын объективті заңдылықтар

2. ДӘРІСТІҢ ҚЫСҚАША КОНСПЕКТІЛЕРІ

Кіріспе

Статискалық физиканы термодинамика мен салыстырғанда айтылғанымыз материяның жылулық қозғалысының модельдік немесе атомдык теориясы деп саналады. Статистиқалық теорияның негізіне заттың динамикалық моделін пайдаланып, сол моделдің микроскопиялық күйлерінің априорлық ыктималдығын болжайды. Әрі қарай белгілленген теория динамикалық микрожүйенің статискалық теориясы боп белгіленеді, яғни оның карастыратыны динамикалық шамалар мен микрокүйлер емес, тек қана олардың ыктималдығы және орташа мәндері.

Статистакалық физика екі үлкен бөлімдерден құралады: жүйелердің тепе-теңдік күйінің теориясы және тепе-теңдік емес процестердің теориясы. Бірінші жағдайда, термодинамикалық жүйелердің тепетеңдік күйін карастырғанда, статистиқалық физиканың пайдаланатын ықтималдыктар және арташа шамалар уақытқа тәуелсіз болады, ал екінші жағдайда ықтималдық және орташа шамалардың мәндері уақытқа тәуелді болады. Тағыда статистиқалық физиканың басқа екі бөлімін қарастыруға болады. Ол - классикалық және кванттық статистикалық физика.

Классикалық статистикалық физикада термодинамикалық жүйені кұрастыратын атомдар мен молекулалар тек қана механиқалық касиеттерге ие болдыда, яғни тек қана механикалық заңдарына бағынады деп саналады. Бұл жағдайда заттың классикалық мөделі құрастырладыда, соның статистикалық каситеттерін зерттейтін теория классикалық статистика деп аталады. Егерде термодинамикалық жүйені кұрастыратын бөлшектер кванттық касиеттерге ие болса, онда сол жүйенің статистикалық касиет-тернін қарастыратын теория кванттық статистика деп саналады. Термодинамикалық жүйлерде тепетеңдік емес процесстерін зерттеу үшін кинетикалық теорияны пайдаланады. Оларды классикалық немесе кванттық кинетика деп атайды.

Сондықтан, айтылғаннан қортындыны алсақ, статистиқалық физика төрт бөлімнен құралады:

классикалық статистика
классикалық кинетика
кванттық статистика

4. кванттық кинетика

Жалпылай, cтатискалық физиканың негізі американ физигі ДЖ. Гиббстің әдістемесіне орналасқан.

Тақырып: Физикадағы 2 әдіс. Лиувилл теоремасы. Статистикалық ансамбль, үлестірілу функциясы.

Көп бөлшектерден құралатын заттардың қасиеттерін зерттеуеге механикалық көзқарас пайдаланды. 18 ғасырда механика ғылыми түрінде ең жоғары деңгейіне жетті. Жалпы, барлық табиғатта өтетін құбылыстарды, бір біріне себепті салдары байланыс арқылы қарастырылды. Ондай көзқарас механикалық детерменизм деп аталды. Механикалық детерменизм бойынша барлық табиғатта өтетін құбылыстар бір- біріне себепті салдар боп саналды. Барлық Ньтонның механикасы механикалық детерменизм тұжырымынан құралада. Табиғатта кездесетін құбылыстардың себепті пікірліктен шыққан қатаң бірізділігі олардың әрқашан міндетті орындалатынын тағдырын белгілейді. Бұл жағдайларда кездейсоқ құбылыстар кездеспейтін боп саналады. Механикалық детерменизмның философтарына құбылыс әрқашанда салдар мен себептің қосындысы боп саналады. Әрине механикалаық детерменизм принципы біріншіден физикалық жүйенің күйін зерртеуге пайдаланды. Егер макроскопиялық көзқарасты алсақ, онда бір белгіленген физикалық жүйенің күйі анықталған болып шығда, егер сол жүйені құрайтын бөлшектердің мекен жайлары мен және олардың қозғалыстары белгілі болса, механикалық заңдары арқылы бөлшектердің, яғни физикалық жүйенің, болашақ жағдайларын анықтауға болады.

Онда детерменизм принцип бойынша физикалық жүйенің қазырғы қүйін біле тұрып, физикалық жүйенің күйлерінің уақыт бойынша өзгерісін анықтауға болады. Осы келтірілген детермениз принципы физикалық жүйенің күйін зерттеуге пайдаланатын нақты механикалық әдіс бөп саналады. Көп болшектерден құралатын физикалық жүйенің күйін механикалық қөзқарас арқылы шешілмейтін тұжырым мұндай қойылған мақсатты басқаша қарастыруға жол салады. Ондай, басқаша көзқарас ─ статистикалық тәсілі деп аталады. Осы жаңа белгіленген статистикалық тәсіл біріншіден көп бөлшектерден құралатын физикалық жүйенің өзінің меншікті статистикалық қасиеттері мен байланысты деп білу керек.

Сондықтан, физикалық көп бөлшектерден құралатын жүйлердің өзгешілік қаситеттерін анықтауға жәңа тәсілдерді қолдану керек. Ендігі қойылытын мақсат статистикалық тәсілдерді көп бөлщектерден құралатын физикалық жүйелердің қасиеттерін және оларда өтетін құбылыстарды зерттеуге пайдалану.

Мехниқалық заңдары бойынша кез келген жүйелердің физикалық қасиеттерін микроскопиялық түрінде анықтау үшін өте көп параметрлерінің мәндері белгілі болу керек екенін мен таныстық. Бірақ термодинамикалық тұжырымдыры бойынша физикалық жүйелердің(мыслы газдарды, сұйқтарды немесе сәулелену құбылыстары және т. б. ) қасиеттерін макроскопиялық зерттеуге шектелген параметрлердің мәндерін білу керек. Егер белгіленген физикалық жүйе тепе-теңдік күйін сақтаса, онда олардың қасиеттерерін зерттеуге көбірек оңайлыққа түседі деп санауға болады. Мұндай жағдайда термодинамикалық жүйелердің физикалық жағдайлары қарапайымдай болады да, соны мен қоса оларға сәкес жүйенің параметрлері уақытқа тәуелді болмайды. Расында, егер бір моль газ тепе теңдік күйде болса, онда оның көлемі V, қысымы P және температурасы T оның толық күйін белегілейді. Егер белегіленген физикалық жүйе бұдан да бір аз күрделі болса да бәрі бір оның тепе-теңдік күйінде касиеттерін анықтауға онша көп парметрлердің мәндерін табуға қажетті емес. Көбінесе физикалық жүйелердің қаситтерін зерттегенде олардың макропара-метрлерінің мәндері өзгерілмейді деп саналады, яғни олар өздерінің тепе-теңдік күйін сақтайды. Мұндай жағдайда жүйенің қысымы, көлемі және температрурасы тұрақты болады да, ол термостатта орналсқан боп саналады

Тұрақты температурада және қысымда орналасқан газдың кез-келген тепе-теңдік күйіне өте көп молекулалрдың қозғалысы және мекен жайы сәйкес келеді. Расында, газ өз тепе-теңдік жағдайын сақтасада молекулалары тоқтамайтын хаотикалық, жылыулық (броундық) қозғалысқа қатынасып жатады. Өзара газ молекулалары бір-бірімен әрқашанда кинетикалық энергия, импульстер мен алмасып жатады. Сондықтан, физикалық жүйенің бір күйіне макроскопиялық көзқарасында өте көп (мыңдаған) микроскопиялық күйлері сәйкес келеді. Яғни микроскопиялық күйлері тоқтамайтын өзгерісте болады да, ал термодинамикалық жүйенің макроскопиялық күйі тұрақты боп саналады.

Басқаша, тепе-теңдік физикалық күйін сақтайтын термодинамикалық жүйенің макроскопиялық параметрлері микроскопиялық параметрлерінің функциясы боп саналады. Мысалы, газдың қысымы макроскопиялық параметр түрінде молекулалрдың құйылған ыдыстың қабырғасына микроскпиялық соқтығыстарының қосындысына тәуелді (микроскопиялық параметрлеріне) .

Осыдан статистикалық ансамбль дегеніміз бір-біріне тең емес күйлерде орналасқан көп нақты жүйелердің қосындысы деп атауға болады.

Олар жүйенің бір күйіне сәйкес боп саналады. Бірақ бір-біріне тең емес жүйенің макрокүйлерінің сандары бір біріне тең емес микрокүйлер арқылы анықталады. Сонда қандай макрокүйлерге сәкес келетін микрокүйлердің саны жоғары болса, соншама сол микрокүйдің жағдайы орнықты болады. Осы белгіленген түсініктілер арқылы жүйенің термодинамикалық ықтималдығы деген ұғымы еңгізіледі.

Кез-келген жүйенің күйінің термодинамикалық ықтималдығы дегеніміз сол жүйенің күйіне сәйкес келетін микроскопиялық күйлерінің саны боп саналады. Сондықтан жүйенің термодинамикалық ықтималдығы дегеніміз сол жүйенің күйін белгілейтін микроскопиялық күйлерінің саны арқылы анықталатын болады. Осы анықтамадан жүйенің термодинамикалық ықтималдығының мәні әрқашанда бірден көп деп белгілеуге болады.

Белгіленген термодинамикалық ықтималдық ұғымы және математикалық статистиқалық заңдары көп бөлшектерден құралатын жүйелердің қасиеттерін зерттеуге статистиқалық физикада пайдаланады.

Ендігі қойылытан мақсат өткенде ең біріңші американ физигі Дж. Гиббс орнаған статистиқалық физиканың жалпы әдісіменен танысамыз.

Егер қарстырылатын термодинамикалық жүйе N материалдық нүктелерден құралатын болса, онда ол жүйеге арналған (5. 2) Гамильтон өрнектерін шығарсақ десек, онда олардың шешімін 6 N бірінші интеграл түрінде келтіруге болады:

$\left\{ \begin{array}{r} p_{1}\left( c_{1}, c_{2}, \ldots, c_{6N}, t \right) = 0 \\ p_{2}\left( c_{1}, c_{2}, \ldots, c_{6N}, t \right) = 0 \\ \ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots \\ p_{3N}\left( c_{1}, c_{2}, \ldots, c_{6N}, t \right) = 0 \\ q_{1}\left( c_{1}, c_{2}, \ldots, c_{6N}, t \right) = 0 \\ \ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots. . \\ {q_{3N}(c}_{1}, c_{2}, \ldots, c_{6N}, t) = 0 \end{array} \right. \$ (5. 3)

Алынған 6N теңдеулер жүйенің фазалық кеңістігінде қозғалыс теңдеуі деп санауға ыңғайлы. Фазалық кеңістік деп 6 N көпөлшемді жалпыланған координаталар мен импульстердің арқылы ойда елестетін кеңістік белгіленеді.

Статистикалық физикада фазалық кеңістіктің екі түрін қарастырады. Бірінші $\mu$ -кеңістік және екіншісі Γ - кеңістік. $\ \mu$ -кеңістік ол бір бөлшекке қатанасты фазалық қеңістік боп саналады. Бір бөлшектің еркін дәреже саны 3 тең болса, онда фазалық μ-кеңістікке 6 өлшемді кеңістік сәйкес келеді (3 жалпылыған координаталарды және 3 жалпыланған импульстерді есептегенде) . Екіншісі Γ - кеңістік деп аталатын фазалық кеңістіктің, көп болшектерден құралатын физикалық жүйелерге еңгізледі. Осыдан, әрқашанда $\mu$ -кеңістік Γ - кеңістіктіктің бір бөлшекке арналған қарапайым түрі деп санауға болады.

Кез келген физикалық жүйенің микрокүйі(фазасы) ондай 6N көпөлшемді кеңістікте бір нүкте мен бейнеленеді. Онда барлық қеңістіктің көлемін жүйенің микрокүйлері толтырады да сондықтан ол фазалық қеңістік деп аталады. Егер карастырылатын жүйе байланысқан болса немесе бөлшектерінің ішкі еркін дәрежелік саны 3N емес f тең болса, онда жүйенің фазалық кеңістігі 2 f -өлшемді болады. Яғни кез-келген термодинамикалық жүйеге меншікті қаситеттеріне сәйкес фазалық кеңістікті белгілеуге болады.

Нақты физикалық жұйе бір белгіленген уақытта бір күйінде болу керек. Ол күйі әрқашанда фазалық кеңістігінде белгілі нүктемен бейленеледі. Бірақ физикалық жүйені құрайтын бөлшектер тоқталмайтын қозғалысқа қатнасады, яғни жүйенің күйі ылғи өзгеріп отырады. Термодинамикалық жүйенің күйінің өзгерісі фазалық кеңістікте кей бір сызық пен белгіленеді ол фазалық траектория деп аталады. Алдында көрсетілген (5. 3) 6N теңдеулер фазалық траекторяның параметрлік теңдеулері боп саналады.

Енді физикалық жүйенің фазалық траекториясынң қаситтерін анықтауға болады. Жүйенің кез-келген траекториясы фазалық қеңістікте 6N бастапқы шарттарымен анықталады (бір бастапқы нүкте мен), яғни жүйенің бөлшектерінің берілген бастапқы уақыт t = 0 болғанда 3N жалпыланған координаттардың мәндері мен және 3N жалпыланған импульстердің мәндері мен. Фазалық кеңістікте жүйенің траекториялары тұйық болсада, бір бірі мен ешқашанда қиылыспайды. Басқаша айтқанда фазалық кеңістіктің әр нүктесінен тек қана бір фазалық траектория өтеді. Бұл тұжырым механиқалық жүйеге арналған (5. 2) теңдеулердің шешімдері бірдей бастапқы шарттарда бірмәнділік болу тиісті қасиеттерінен алынады.

Егер шектелген термодинамикалық жүйені қарастырсақ, онда оның толық энергиясы тұрақты болу керек, яғни:

$E = E\left( q_{1}, q_{2}, \ldots p_{1}, p_{2}, \ldots \right) = \ const$ (5. 4)

Осы алынған өрнек жүйенің барлық параметрлерін бір-бірімен байланыстырады оны басқаша энергияның жүйенің фазалық кеңістегіндегі гипербет теңдеуі боп саналады. Оны жайында фазалық кеністіктегі энергияның беті деп атауға болады. Шектелген жүйенің қандай өзгерістері боласада оның фазалық траекторяисының барлық нүктелері жүйенің энергиясының гипербетінде орналасады. Бірақ жалпы түрінде бір ғана жүйенің өзгерісін зертемейді, соны мен қоса көп жүйелердің (ансамбілдердің) қосындысын қарастыру керек болады. Бұл жағдайларда ондай күрделі жүйе (ансамбль) фазалық көлемінде таралатылған боп саналады. Ондай күрделі фазалық көлем 2 fN өлшемді болады. Зерттеуге ыңғайлы болу үшін элементарлық фазалық көлем деген ұғымын пайдаланады. Элементарлық фазалық көлем дегеніміз:

$d\Omega = dq_{1}, dq_{2}, \ldots, dq_{3N}, dp_{1}, dp_{2}, \ \ldots, dp_{3N}$ (5. 5)

Егер элементарлық фазалық көлемді барлық фазалық кеңістігіндегі қосындысын алсақ, онда шектелген жүйенің толық фазалық көлемі мынандай интегрлаға тең болады:

$\Omega = \int_{}^{}{\ldots\int_{}^{}{dq_{1}}}, dq_{2}, \ldots dp_{1}, dp_{2}\ldots$ (5. 6)

Мында фазалық кеңістіктің көлемі 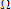жалпыланған кооринаталар мен импульстерге тәуелді. Соны мен қоса ол жүйенің толық энергиясына тәуелді боп саналады. Әрине мұндай тұжырым жүйенің энегргиясының жалпыланған импульстерге және координаталарға тәелділіктен алынады. Яғни $E = E\left( q_{1}, q_{2}, \ldots p_{1}, p_{2}, \ldots \right)$ , сондықтан:

$\Omega = \Omega(E)$ (5. 7)

Егер энергияның E, E +dE интервалындағы өзгерісін алсақ, онда сол микроинтервалға сәйкес келетін фазалық кеңістіктіктің элементарлық көлемінің мөлшері тең болады:

$d\Omega = \ \frac{\partial\Omega}{\partial E}dE$ (5. 8)

Ендігі қойылытын мақсат статистикалық әдісті көп бөлшектерден құралатын термодинамикада танысқан ұғымдар арқылы жүйелердің қасиеттерін зерттеуге пайдалану.

Алдына Гиббс әдісін көп бөлшектерден құрлатын термодинамикалық жұйелердің қасиеттерін анықтауға пайдаланады деп белгіледік.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.