Көпбұрышты фигураларына қатысты анықтамалар

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 20 бет
Таңдаулыға:

Мазмұны

Кіріспе
3
1
Геометриялық материалды оқып үйрету әдістемесі
5
1.1
Көпбұрышты фигураларына қатысты анықтамалар
6
2
Көпбұрыштардың түрлері
8
2.1
Көпбұрыштар тақырыбын оқыту әдістемесі
10
2.2
Көпбұрыштар ұғымынның маңызы, тарихы және қолданысы
15

Қорытынды
18

Пайдаланылған әдебиеттер тізімі
19

Қосымша
20

Кіріспе

Жұмыстың өзектілігі. Қазақстан дербес мемлекет ретінде тәуелсіздігін алғаннан бері қоғам дамуының қазіргі талаптарынан туындап отырған міндет пен мақсаттарға орай өскелең ұрпаққа білім мен тәрбие беру мәселесін жан-жақты жетілдіру қажет болып отыр.
Әрине, бұл білім беру жүйесінің барлық буындарына, соның ішінде бастауыш буынға, зор жауапкершілік жүктейді. Өйткені, білім мен тәлім - тәрбиенің негізі бастауыш мектепте қаланады.
Осы бағытта біршама шаралар жүзеге асырылуда. Атап айтқанда: бастауыш мектепте оқытылатын пәндерден жаңа мемлекеттік стандарт, бағдарламалар жасалып, соларға сәйкес төлтума оқу-әдістемелік кешендер жазылды, демек, оқу - тәрбие процесін ұйымдастырудың жаңа жүйесі мектептердің тәжірибесіне енгізілуде, яғни педагогикалық ғылымның озық идеялары мен жинақталған тәжірибелердің нәтижелері жаңа жағдайларда өзінің қолданысын тауып отыр.
Осындай күрделі мәселенің дұрыс шешілуі ұстаздардың теориялық білімінің және кәсіби мамандығының деңгейіне тәуелді. Сондықтан, оқушыларға тек қана білім берумен шектеліп қалмай, қазіргі заман талабына сай тәлім-тәрбие беретін, оқушылардың ой-өрісін, қабілетін жан-жақты дамытуға толық мүмкіндік туғызатындай дайындығы бар мамандар дайындаудың қажеттігін ескеруге тура келеді.
Сондықтан да мектептегі оқу процесінің негізгі мақсаты - арнайы педагогикалық әдістермен мақсатты және жүйелі түрде оқушылардың интеллектін, шығармашылық ойлауын дамыту, ғылыми көзқарасы мен белсенділігін қалыптастыру, әр адамның бойындағы туғаннан пайда болған интуициясын әрі қарай дамытуға ықпал ету, оқушының табиғи қасиеттерін, математикалық білім деңгейін тереңдету үшін оқытуды жоспарлы түрде ұйымдастыру, өз бетінше білім алу дағдыларының дамуына негіз салу болып табылады.
Жұмыстың мақсаты. Көпбұрыштар тақырыбын оқыту әдістемесімен талқылау, көпбұрыштар жайлы ақпараттармен таныстыру.
Жұмыстың міндеттері.
1) геометриялық фигуралар туралы түсініктерін қалыптастыру;
2) сызбалық және өлшеуіш аспаптардың көмегімен және оларды пайдаланбай (көзбен өлшеу, қолдан сызу, т.с.с.) оқушыларда өлшеудің және геометриялық фигураларды салудың машықтық біліктерін қалыптастыру;
3) кеңістік ұғымдары жөніндегі білімдерін жалпылау;
4) геометриялық материалдарды оқыту әдісінің оқушылардың пәнге қызығушылығын оятудағы тиімділігін тәжірибе жүзінде тексеріп, зерттеу нәтижесінде ғылыми-әдістемелік нұсқау жасау, оны дәстүрлі оқыту әдістерінің нәтижелерімен салыстыру.
Проблема. Елдің болашағы оқу-тәрбие ісіне тәуелді. Сондықтан да оқу-тәрбие ісіне келелі міндеттер жүктелгендігін ескеріп, жаңа қоғам мүддесіне лайық, жан-жақты жетілген, бойында ұлттық сана, ұлттық психология қалыптасқан ертеңгі қоғам иелерін тәрбиелеп өсіру отбасының, мектептің міндеті.
Бүгінгі күн дидактика саласындағы орнықты мәселелердің бірі - математика пәні бойынша оқушылардың геометриялық ұғымдарын қалыптастыру проблемасы. Математика пәнін оқытудың тәжірибесі геометриялық материалдарды оқытудың тиімді әдістемесіне қол жеткізді, екіншіден, оқушының осы ұғымдарды игере отырып өзіндік білім алуы, өмір тәжірибесін жинақтау қажеттілігі.
Зерттеу әдістері:
1) зерттеу тақырыбына байланысты әдебиеттермен танысып, оларға ғылыми әдістемелік тұрғыдан талдау жасау;
2) алдыңғы қатарлы мұғалімдердің іс-тәжірибесімен танысу;
3) дәстүрлі оқыту әдістері мен ұсынылған оқыту әдісіне салыстырмалы талдау жасау.
Жұмыстың ғылыми-практикалық пайдасы.
1) ұсынылып отырған зерттеу жұмыс мектепте оқушылардың пәнге қызығушылығын оятуға игі әсерін тигізеді және геометриялық фигураларды сапалы игеруге көмектеседі;
2) геометриялық материалдарды оқыту негізінде оқушылардың геометриялық ұғымын қалыптастыруға арналған тапсырмалардың мектеп мұғалімдерінің іс-тәжірибесінде қолдануға кең мүмкіндіктің болуында.
Жұмыс құрылымы: жұмыс кіріспеден, бес бөлімнен, қорытындыдан, пайдаланылған әдебиеттер тізімінен, қосымшадан және 23 беттен тұрады.

1 Геометриялық материалды оқып үйрету әдістемесі

Геометриялық материалды оқып үйренудің негізгі міндеттері оқушылардың нүкте, түзу сызық, түзу кесінді, сынық сызық, бұрыш, көпбұрыш, дөңгелек сияқты геометриялық фигуралар туралы айқын түсініктерін және алғашқы ұғымдарын қалыптастыру болып табылады.
Мұнда геометриялық мазмұнды жаттығулар мен есептер жүйесі және олармен жұмыс істеу әдістемесі балаларда кеңістік ұғымының, бақылау, салыстыру, абстракциялау және жалпылау біліктерінің дамуына ықпал жасауға тиіс.
Оқыту міндеттерінің бірі - оқушыларда чертёждік және өлшеуіш аспаптардың көмегімен және оларсыз (көз мөлшерімен өлшеу, қолдан сызу, т.с.с.) өлшеудің және геомтриялық фигураларды салудың практикалық біліктерін қалыптастыру болып табылады. Сондай-ақ салулар мен өлшеулер туралы алғашқы түсінік берген жөн.
Бағдарлама белгілеген есептерді ескере отырып, геометриялық материалды оқып үйренгенде, әр түрлі көрнекі құралды пайдалану керек болады. Олар түсті картоннан немесе қалың қағаздан жасалған демонстрациялық, жалпы сыныптың геометриялық фигуралардың модельдері әр түрлі формадағы нәрселердің, фигуралары кескінделген плакаттар, сондай-ақ геометриялық фигуралар, тақтадағы чертёждар, диафильмдер. Сонымен қатар жеке көрнекі құралдар: жолақ қағаз; ұзындықтары әр түрлі таяқшалар, қағаздан қиып алынған фигуралар және фигуралардың бір бөлігі сияқты үлестірмелі материал талап етіледі. Жеке тақырыпты оқып үйренгенде балалармен қолдан мынадай көрнекі құралдар жасаған пайдалы: тік бұрыштың моделі, бұрыштың жылжымалы моделі (малка), палетка, ауданды өлшеу бірліктерінің моделі т.б.
Тақтада чертёждерді орындау үшін сыныпта чертёждік-өлшеуіш аспаптар жиынтығының: сызғыштың, чертёждік үшбұрыштың, циркульдың болуы қажет. Осы тәрізді аспаптар әр оқушыда болуы тиіс.
Геометриялық материалды оқып үйренудің неғұрлым тиімді әдісі болып табылатын мына сияқты лабораториялық-практикалық әдістер: қағаздан, таяқшалардан, сымнан фигуралардың модельдерін жасау; сызу, өлшеу т.б. Мұнда елеусіздеу белгілерін (түсі, өлшемі, жазықтықта орналасуы т.т.) өзгертіп ала отырып объектілердің алуан түрлілігін қамтамасыз етудің, балаларға елеулі белгілерін - нәрселердің формасын, фигуралардың қасиеттерін т.б. айырып көрсете білуді меңгеруіне көмек берудің маңызы зор.
Геометриялық түсініктер мен ұғымдарды қалыптастыру өздігінен және мейлінше айрықша бағытты ұстана отырып, орындалатын болса да мүмкін болатын жерде сабақта геометриялық материалды оқып үйрену арифметикалық және алгебралық материалды оқып үйренумен байланыстырылуы тиіс.
Оқушылар геометриялық материалдың мәнін аша отырып, нәрселердің формасы, өлшемдері және кеңістіктегі өзара орналасуы туралы алғашқы түсінікті балалар мектепке дейінгі кезеңде-ақ жинақтайды. Ойын процесінде және практикалық қызметінде олар нәрселерді пайдаланып отырады, оларды қарайды, қолдарымен ұстап көреді, суретін салады, пластилиннен жасайды, конструкциясын жасайды және басқа қасиеттерінің ішінен олардың формасын бөліп көрсетеді. Мектеп жасына дейінгі көптеген балалар шар, куб, дөңгелек, квадрат, үшбұрыш, тік бұрыш формалы заттарды дұрыс көрсете алады. Алайда ұғымдарды жалпылау дәрежесі онша жоғары болмайды: балалар квадратты тік бұрышпен шатастырады, егер нәрсенің өзі оларға таныс болмаса, ол заттың таныс формасын тани алмайды. Фигуралардың қабырғалары мен бұрыштарының әдеттенбеген қатыстары; жазықтықта әдеттегіден басқаша орналасуы, тіпті фигуралардың өте үлкен және өте кішкене өлшемдері баланы шатастырады. Фигуралардың аттарын балалар көбінесе нәрселердің аттарымен шатастырады немесе ауыстырып айтады (мысалы, балалар үшбұрышты бұрыш, қақпақ, жалауша т.с.с. деп атайды).
Егер санақ басы орны баланың өзі болса, онда нәрселердің кеңістіктегі орнын сипаттай отырып, мектеп жасына дейінгі балалар кеңістік қатынастарды (оның өзіне қатысты алғанда сол жақтан - оң жақтан, алдыңғы жақтан - артқы жақтан, жоғарыда - төменде, жақынырақ - алысырақ т.с.с.) еркіндеу тағайындай алады. Баланың нәрселердің жазықтықтағы немесе кеңістіктегі, басқа нәрсеге немесе басқа адамға қатысты алғандағы, орналасу қалпын тағайындауы анағұрлым қиынырақ.
Мектепте оқытқанда балалардың тәжірибесіне сүйену, олардың түсініктерін тиянақтау және байыта түсу қажет.

Көпбұрышты фигураларына қатысты анықтамалар

Көпбұрыш сөзі бұл отбасындағы барлық пішіндердің көптеген бұрыштары бар екенін білдіреді. Бірақ бұл фигураны сипаттау үшін жеткіліксіз.
Көпбұрыш - бұл әдетте жазықтықтың бөлігі ретінде анықталған, жабық сынықпен шектелген геометриялық фигура. Егер шекара сызығында өзін-өзі қию нүктелері болмаса, көпбұрыш қарапайым деп аталады. Мысалы, үшбұрыштар мен квадраттар қарапайым көпбұрыштар, ал бес бұрышты жұлдыз көпбұрышты болып саналады. Көпбұрыштың бір түрі 1-суретте көрсетілген.
Сынған шыңдар көпбұрыштың шыңдары деп аталады, ал оның байланыстары көпбұрыштың жақтары деп аталады. Көпбұрыштың жақтарының саны оның шыңдарының санына сәйкес келеді.
Көпбұрышты анықтаудың үш түрлі нұсқасы бар, соңғы анықтама ең көп таралған:
жазық тұйық сынық - неғұрлым жалпы жағдайы;
тегіс жабық сынық өздігінен қиылысусыз, кез-келген екі көрші
байланыс бір түзу сызықта тұрмайды;
өздігінен қиылыспайтын жабық сынықпен шектелген жазықтықтың
бөлігі-жалпақ көпбұрыш; бұл жағдайда сынықтың өзі көпбұрыштың контуры деп аталады.
Сондай-ақ, бұл анықтаманы жалпылаудың бірнеше нұсқалары бар, олар сынған байланыстардың шексіз санына, кеңістіктегі сынған бірнеше байланыссыз шекаралық сынықтарға, түзу сызықтардың орнына үздіксіз қисықтардың ерікті сегменттеріне және т.б.
Қатысты анықтамалар:
көпбұрыштың шыңдары көршілес деп аталады, егер олар оның бір
жағының ұштары болса;
көпбұрыштың жақтары іргелес деп аталады, егер олар бір шыңға
сәйкес келсе;
көпбұрыштың барлық жақтарының жалпы ұзындығы оның
периметрі деп аталады;
көпбұрыштар үшін диагональ екі іргелес емес шыңдарды қосатын
кесінді болып табылады;
берілген шыңдағы жалпақ көпбұрыштың бұрышы (немесе ішкі
бұрышы) - бұл шыңға жақындаған екі жақтың арасындағы бұрыш. Егер көпбұрыш дөңес емес болса, бұрыш 180 0 асып кетуі мүмкін. Қарапайым көпбұрыштың бұрыштарының саны оның жақтарының немесе шыңдарының санына сәйкес келеді;
берілген шыңдағы дөңес көпбұрыштың сыртқы бұрышы деп - бұл
шыңдағы көпбұрыштың ішкі бұрышына іргелес бұрыш.
Кәдімгі көпбұрыштың ауданы апофемаға (биіктікке) көбейтілген периметрдің жартысына тең. Жақтар санының өсуімен көпбұрыш шеңберге, ал апофема радиусқа ұмтылады. Бұл шеңбердің ауданы шеңбердің радиус ұзындығының жартысының көбейтіндісіне тең деп санауға негіз береді.

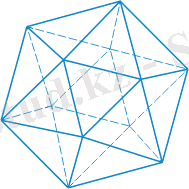
1-сурет - Көпбұрыштың кескіні

2 Көпбұрыштардың түрлері

Көпбұрыш - жазықтықтағы кез келген тұйық сынық сызық. Сынық сызықтың әрбір бөлігі көпбұрыштың қабырғасы, ал олардың ұштары көпбұрыштың төбелері деп аталады. Егер сынық сызық қарапайым болса, онда көпбұрыш қарапайым көпбұрыш деп, ал күрделі болса, жұлдыз тәрізді көпбұрыш деп аталады.
Көпбұрыш жазықтықты бірнеше облысқа бөледі. Қарапайым көпбұрыш жазықтықты біреуінде түзу толығынан жататын, ал екіншісінде толық жатпайтын екі облысқа бөледі. Біріншісін көпбұрыштың сыртқы облысы, екіншісін ішкі облысы дейді. Көпбұрыш осы облыстардың шекарасы болады. Көпбұрыш пен оның ішкі облысын біріктірсек, екі өлшемді көпбұрыш шығады. Егер көпбұрыштың төбелері кез келген қабырғасы арқылы жүргізілген түзудің бір жағында жатса, онда оны дөңес көпбұрыш дейді.
Төбесі арқылы өтетін қабырғалардың ішкі облыс жағынан жасайтын бұрышын көпбұрыштың ішкі бұрышы дейді.Тұрақты көпбұрышбарлық жақтары мен бұрыштары тең дөңес көпбұрыш.
Кез келген көпбұрыш жазықтықты екі облысқа бөледі: ішкі және сыртқы. Ішкі аймақ деп те аталады көпбұрыш. Басқаша айтқанда, мысалы, пентагон туралы айтқанда, олар оның бүкіл ішкі аймағын да, шекарасын да білдіреді. Және көпбұрыштың ішінде орналасқан барлық нүктелер ішкі аймаққа жатады, яғни. нүкте пентагонға да қатысты (2-суретті қараңыз).

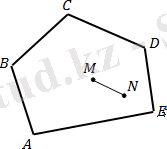
2-сурет - Пентагон. Дөңес көпбұрыш

Көпбұрыштарды кейде белгісіз бұрыштардың (n дана) болуының жалпы жағдайы қарастырылатынын атап өту үшін n-гондар деп те атайды.
Көпбұрыштың периметрі - көпбұрыштың жақтарының ұзындықтарының қосындысы. Енді біз көпбұрыштардың түрлерімен танысуымыз керек. Олар екіге бөлінеді дөңес көпбұрыш және дөңес емес көпбұрыш.
Егер көпбұрыштың барлық қабырғалары мен ішкі бұрыштары өзара тең болса, онда оны дұрыс көпбұрыш деп атайды. Дұрыс көпбұрыш әрқашанда дөңес болады. Тек үшбұрыштың ғана қабырғаларының теңдігінен бұрыштарының теңдігі шығады. Жалпы жағдайда олай болмайды. Қабырғалары тең, бірақ бұрыштары әр түрлі n бұрышты көпбұрыш (n3) және бұрыштары тең, бірақ қабырғалары әр түрлі n бұрышты көпбұрыш болуы мүмкін. Дұрыс көпбұрыштың барлық төбелері арқылы өтетін сырттай шеңбер сызуға болады.
Дұрыс көпбұрыштар дегеніміз барлық қабырғалары және іргелес жатқан қабырғалар арасындағы бұрыштары тең фигуралар. Мысалы тең қабырғалы үшбұрыш дұрыс көпбұрыш болады 3-суретте көрсетілген.

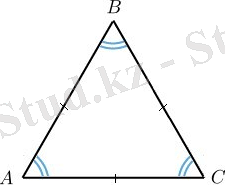
3-сурет - Дұрыс көпбұрыш

Осы үшбұрыштың барлық қабырғалары және іргелес жатқан қабырғалар арасындағы бұрыштар тең болады. Басқа дұрыс көпбұрыштар мысал ретінде 4-суретте көрсетілген.

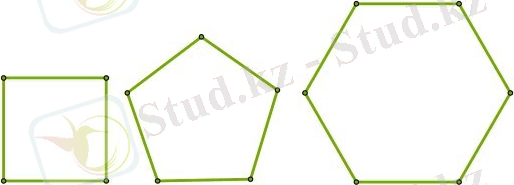
4-сурет - Дұрыс көпбұрыштар тізімі

Дұрыс көпбұрыштың іргелес жатқан қабырғаларының арасындағы бұрыш мына формула арқылы аңықталады:

a = 180 · (n - 2) : n (1)

Мысалы дұрыс үшбұрыш үшін n=3, a = 180 · (3 - 2) : 3 = 600
Ал квадрат үшін n=4, a = 180 · (4 - 2) : 4 = 900.
Бесбұрыштан бастап дөңес емес дұрыс көпбұрыш (өзара қиылысатын немесе жұлдызшалы) кездеседі. Олардың барлық қабырғалары тең, барлығының бұрыштары тең және бағыттары бірдей болады. Мұндай көпбұрыштардың төбелері бір шеңбердің бойында жатады. Көпбұрыш дөңес деп аталады, егер түзу сызық оның кез-келген жағы арқылы жүргізілсе, бүкіл көпбұрыш осы сызықтың бір жағында ғана болады. Барлық басқа көпбұрыштар дөңес емес 5-суретте көрсетілген.

5-сурет - Дөңес емес көпбұрыш

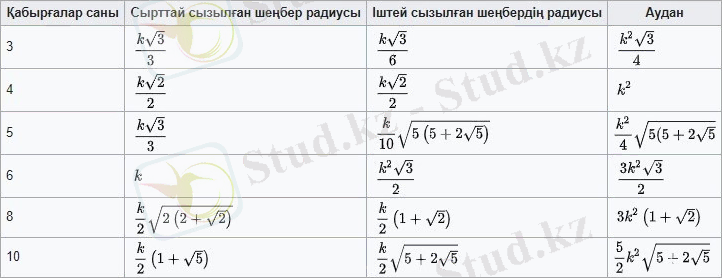
Төмендегі 1-кестеде дұрыс көпбұрыштар қабырғаларының саны және оларды сырттай және іштей сызылған шеңберлерді радиустарының ұзындығын, көпбұрыштардың аудандарын анықтайтын формулалар топталған. Дұрыс көпбұрыштың қабырғасының ұзындығы - k әріпінемен белгіленген.

1-кесте - Көпбұрыштардың ауданын анықтайтын формулалар

2.1 Көпбұрыштар тақырыбын оқыту әдістемесі

Сабаққа қойылатын ең негізгі талаптардың бірі - оның мақсаттылығы. Көпбұрыштар тақырыбын оқыту әдістемесі жөніндегі әдебиеттерден ең алғаш сабақтың дидактикалық мақсатттары, бұдан соң бұл тақырыптың мазмұны арқылы тәрбие берудің, оқушы білімін жетілдіруді көздейтін негізгі мақсаттар туралы ұсыныстарды табуға болады. Сабақтың мақсаты оқушыға түсінікті болуы керек. Сабақтың ұйымдастырылуы оқушыны қызықтырып, белсендігін арттыруы тиіс.
Мектеп мұғалімі оқушының танымдық белсенділігін арттыруға жеткілікті сабақ ұйымдастыруы керек. Сабақтың жалпы мақсаты, мазмұны мен құрылымы жаңа сабақтарда байқалуы керек.
Сабаққа қойылатын екінші бір басты талап - сабақ мазмұнын дұрыстап орналастыра білу. Математика сабақтарындағы ең маңызды мәселе - оның мазмұны.Қарастырып отырған пәнді логикалық тұрғыда терең бейнелеу керек. Тек математика сабағының мазмұны арқылы білім, білік, дағды қалыптасады және математикалық фактілерді, математикалық әдістерді қолдану арқылы сабақ мазмұнын дамытуға болады. Егер сабақты жаңа тақырыпты түсіндіру жоспарланған болса, онда сабақты дедуктивтік ой қорыту жолымен дәлелдеу, талдау жасап, оқушылардың қаншалықты меңгергенін білу үшін мұғалім мақсатты жұмыстармен айналысады.
Сабақ мазмұнының барлық түрлерін жоспарлы, белгілі жүйеде оқыту керек. Сондықтан әрбір сабақтың негізгі мазмұнын білу арқылы, солардың төңірегінде материалдар жинастыру керек. Сабаққа қойылатын үшінші талап ол - сабаққа қажетті жабдықтар мен әдістерді, оқытудың тәсілдерін, сабақ кезінде тәрбие берудің тиімді әдістерін таңдап алу. Сабаққа аса қажетті жабдықтарды, әдістер мен тәсілдерді таңдап алу мұғалімнің шеберлігіне байланысты жұмыс.
Мұғалім жұмысының табысты болуы оқушылардың жалпы дайындығына, олардың жеке ерекшелігіне, сабаққа керекті жабдықтардың тиімділігіне және оқу материалының ерекшелігін мұғалім қаншалықты дәрежеде айта білді, оқу жұмысында танымдық мәселелерді оқушылар алдына қаншалықты дәрежеде қоя білуіне тікелей байланысты. Оқыту жұмысында кез келген құрал-жабдық, дәріс, тәсілдердің ешбірі универсалдық сипатта бола алмайтынын ескеру керек. Тек бір әдіс не тәсілдің өзін ғана пайдалану нәтиже бермейді.
Оқытуда негізгі мәселе көрнекі жабдықтар әр түрлі формада қолданылуы тиіс. Сондықтан сабақта көрнекі және техникалық құралдарды кешенді түрде пайдаланып және кітаппен істелетін жұмыс түрлерін көбейту керек. Математикалық ұғымдардың абстракциялық сипаты оқушылардың түсінуін қиындатады. Бұл қиындықты пәндік модельдер, графиктік, таңбалы т.б. модельдер арқылы жоюға болады.
Көпбұрыштар тақырыбын меңгеру барысында әр түрлі күрделі мәселелерді жай түрде баяндағанда суреттер мен сызбалар қарастырылатын негізгі ұғымды сипаттайтын көрнекіліктер қолданылады.
Сабаққа қойылатын төртінші талап - оқушылардың оқу әрекетін әр түрлі формада ұйымдастыру. Өз бетінше білім алу, өзін-өзі бақылау, бағалау, оқу әрекетін жекеше ұйымдастыруды дамыту талабын алға қояды және сабақтарда оқушылар көрнекіліктерді қолданады және топтық жұмыс формасын пайдаланады.
Ғылыми - техникалық прогресстің жедел дамуы, ғылым мен өндірістің біте қайнасуы ой еңбегін одан әрі жетілдіруді талап етеді. Қазіргі таңда оқушының жалпы даму деңгейі, оның ойлауы мен өздігінен білім алу іскерлігі, алған білімін іс жүзінде қолдана алуы ерекше маңызға ие. Сондықтан ғылым негіздерін оқытып үйреткенде оқушылардың шығармашылық белсенділігін дамыту, олардың өздігінен білім алу іскерлігін қалыптастыру және оны одан әрі өрістету, алған білімін практикада қолдана білу машықтарын шыңдау бүгінгі таңда зор міндет болып табылады. Бұл өзекті мәселені жүзеге асыру күллі оқыту әдістері мен оқу-тәрбие жұмысын барынша жетілдіруді талап етеді.
Көпбұрыштар тақырыбын оқыту барысында оқушылардың өз бетінше істейтін жұмыстарын ұйымдастыру. Бұл тақырыптан өздігінен орындалатын жұмыстар деп берілетін тапсырманы, мұғалімнің басшылығымен не оның тікелей қатысуынсыз, оқушылардың өздері атқаратын жұмыстарын айтамыз. Бұл туралы айтқанда оның өзара тығыз байланысты екі міндетін ескерген дұрыс.
Бұлардың біріншісі - оқушылардың танымдық қызметіндегі іскерлікті, дербестікті дамыту және одан әрі өрістету, оларды білімді өздігінен орындауға, игеруге, дүниеге көзқарасын қалыптастыруға үйрету.
Екіншісі - оқушылардың алған білімін өздігінен іс жүзінде қолдана білуге баулу. Оқушылардың өздігіне атқаратын жұмыстары олардың ой еңбегін қалыпқа келтіруге бағытталған және мұғалімнің берген тапсырмаларын орындаудың ең тиімді тәсілдерін өздеріне іздестіру көзделген.
Сабақтарда оқушылар өздігінен орындайын жұмыстарды былай жіктеуге болады: оқулықпен, оқу құралымен, анықтама әдебиетпен, есептер жинағымен ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.