Сызық инварианттарының есептеу формулалары

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

Мазмұны

Кіріспе
3
1
Сызық ұғымы
4
1.1
Сызық инварианттарының кинематикалық тұрғыда сипатталуы
5
1.2
Сызық инварианттарының есептеу формулалары
6
2
Инварианттардың геометриялық мағынасы
7
2.1
Түзу сызықты бер инварианттардың есептелу формулалары
9
3
Айнымалыларды ауыстыру. Инварианттары мен тензолар
11
3.1
Беттің негізгі инварианттары
14
3.2
Беттегі сызықтық инварианттарының есептеу формулалары
16
3.3
Сызық инварианттарының кинематикалық тұрғыда сипатталуы
18

Қорытынды
20

Пайдаланған әдебиеттер тізімі
21

Кіріспе

Жұмыстың өзектілігі: оқырмандарды инварианттар ұғымымен толықтай таныстыру, соынмен қатар геометриялық есептерде қолданыы мен маңызын көрсету.
Жұмыстың мақсаты: инварианттар ұғымын тоықтай талқылау, қолданыс аясын есептер мен формулалар арқылы көрсету..
ХVIII ғасырда пайда болған ғылым ретіндегі дифференциалдық геометрияның алғашқы анықтамасы, геометрияның кеңістік формалар мен қатынастар ғылымы, атап айтқанда кескіндер және оларды өзара түрлендірулері жөніндегі ғылым ретіндегі бастапқы анықтамасымен байланысты. Дифференциалдық геометрияның өзге геометриялық пәндер ішінен бөлінуі - зерттеу аймағы емес, зерттеу тәсіліне немесе дәлірек айтса, зерттеу аппараттарына байланысты деуге болады. Аналитикалық геометрияның бүгінгі таңдағы мазмұндалуы векторлық алгебра аппаратынсыз мүмкін болмауына ұқсас дифференциалдық геометрия да векторлық анализ - демек мәндері немесе аргументтер жиыны векторлар болып келетін функциялар теориясыннсыз мүмкін емес.
Функциялар теориясында көңіл негізінен инварианттардышығарып алуға, атап айтқанда скаляр аргументін ауыстыруға тәуелсіз немесе векторлық аргумент жағдайында векторлық базисті ауыстыруға тәуелсіз шамаларды алуға аударылады. Бұл бағытта беттер теориясы және өріс теориясының негізгі фактілері оп-оңай алынып, соынмен бірге тензор ұғымының пайда болуы орынды.
Осы аумақты бүгінгі таңдағы жағдайы - көптеген матиматик ұрпақтарының күш жұмсауының нәтижесі. Геометрия дамуының тарихын сипаттаудың қиыншылығы, осы күнгі көптеген геометриялық мәселелер мен идеяларға деген көзқарастың ежелгі математиктердікінен өзгеше болуында. Математикадағы барлығы дерлік геометриялық әдістер жаңаша шыңдалды. Қазіргі көзқарас бойынша, негізгі жайттары осы курстық жұмыста мазмұндалатын геометрия және топология бірнеше негізгі идеяларға негізделеді.
Геометрия және осы күнгі физиканың көптеген іргелі мәселелерінің дамуы мен түсуінде маңызды рөл атқарған бір іргелі қағидаға тоқталмай болмайды. Бұл кеңістіктердің симметриялар группаларына қатысты, геометриялық нұсқалардың инварианттылығы идеяларына негізделген группалық әдістер.
Жұмыс құрылымы: жұмыс кіріспеден, тоғыз бөлімнен, қорытындыдан, пайдаланылған әдебиеттер тізімінен және 21 беттен тұрады.

1 Сызық ұғымы

Аналитикалық геометрияда сызықты анықтайтын функцияларға дифференциалдау шарты қойылмағандықтан, ондағы сызық анықтамасы дифференциалдық-геометриялық зерттеу негізінде жата алмайды. Сол себептен де сызықтың шынайы топологиялық анықтамасы да айтқан зерттеуде қолайсыз.
Біздің енгізетініміз - сөз етккен зерттеулерге ыңғайлы және өзге анықтамаларға қайшы келмейтін сызық ұғымы анықтамасы. Атап айтқанда енгізілетін сызықтар аналитикакалық геометриядағы және топологиядағы сызықтарды қамтиды.
А - кез келген нүктелер жиыны, Д - түзу кесіндінің нүктелер жиыны болсын. А және Д нүктелері араында өзара бірмәнді сәйкестік орнығып, бұл сәйкестік ең болмағанда бір декарт координаталар жүйесінде жеткілікті рет дифференциалданатын екі функциямен бірлесе, А жиынын сызықтың қарапайым үзігі дейміз.
Егер түзу ретінде ОХ осі алынса, онда қарапайым үзік

у=φ(х), z=ψ(х), (1)

теңдеулерімен беріледі, мұнда φ және ψ кейбір DϵOx кесіндісінің барлық нүктелерінде дифференциалданатын функциялар.
Енді жеткілікті рет дифференциалданатын бір айналымға тәуелді

r=r(t), (1.2)

Вектор функция келбетін қарастырайық. Бұл функцияның берілуі r векторының координаталары болып келетін

x = f1 (t), y = f 2 (t), z = f3 (t) (1.3)

скаляр функцияларының беріліуіне эквивалент.
Анализден мындай жәйт мәлім - y - y (х) теңдеуін (y (х) - дифференциалдамалыфункция) M(х,y) нүктесі аймағындах-ке қатысты шешу үшін, М нүктесінде

y (х) 0 (1.4)

болу керек. Сонда х=x(y) шешімі де М нүктесінің кейбір маңында дифференциалданатын функция болып келеді.
Егер берілген t мәнінде fi (t) туындыларының бірі нөлден өзгеше болса, онда (1.3)-тің сәйкес теңдеуін t-ға қатысты шешеміз.

y = f2 (t(x)), z = f3 (t(x)) (1.5)
Кеңістік сызығы (немесе қисығы) деп бір аргументті жеткілікті рет дифференциалданатын r=r(t) вектор-функция келбетін айтамыз. r r(t) орындалатын нүктелер қисықтың жай нүктелері, r=r(t) болатын нүктелер қисықтың ерекше нүктелері делінеді.
Геометриялық тұрғыда r(t) 0 шарты сызықтың жанамасын қамтамасыз етеді. Сонымен сызықтың жай нүктесінде әрқашан білгілі жанама бар.
Ескерту. r(t) 0 шарты сызық нүктесі аймағын қарапайым үзік ретінде келтірудің жеткілікті шарты болып келеді, жалпы алғанда ол қажетті шарт болуы міндетті емес. Дербес жағдайда r -тың нөлге айналуы t айнымалсын ауыстыру нәтежесі болуы мүмкін. Мәселен, t=τ3арқылы жаңа τ айнымалысына көшсек

rt = r (t(τ)) = 3τ 2 rt (1.6)

1.1 Сызық инварианттарының кинематикалық тұрғыда сипатталуы

Френе репері (Френе қозғалмалы үшжағы) қатты денеге тәріздес сызық бойымен бірқалыпты, демек уақыт бірлігі ішінде репердің басы сәйкесінше жол бірлігін өтетіндей қозғалсын, уақыт есебінде алайық:

S = t (2)

Бірдей қисық үзіктерінде қисықтық (немесе бұралымның) абсолюттік шамасы өскен сайын жанама (немесе бинормаль) бағыттарының соншалық өспелі өзгеретіндігін байқаймыз.
Қисықтық пен бұралымның кинематикалық сипаттамасы лездік бұрыштық жылдамдығы векторын енгізу нәтижесінде алынады. Қозғалмайтын нүктеге иолатын қатты дененің қозғалуы, қозғалмайтын түзуге де-l лездік айналу осіне ие болады.
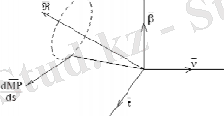
Егер қозғалмайтын нүкте ретінде репердің М басын алса, қатты дененің кез келген Р нүктесінің сызықтық жылдамдығы дененің бұрыштық жылдамдығы прқылы өрнектеледі (1-сурет).

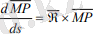(2.1)

Шынында да, айналатын кез келген нүктесі шеңбер бойымен қозғалады, демекғ шеңбердің нүктелері үшін вектор-функциясы тұрақты болып табылады.

1-сурет - Сызықтық және бұрыштық жылдамдықтар

1.2 Сызық инварианттарының есептеу формулалары

Ең алдымен қисықта параметр ретінде S доға ұзындығы алынсын, димек қисық теңдеуімен аламыз.

r=r(s) (2.2)

Френе формуласын түрлендіре қолданамыз

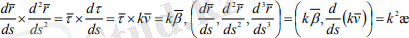(2.3)
Мұның жалғасы ретінде
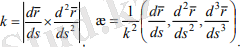(2.4)
r=r(t) вектор-функциясының Sбойынша алғашқы үш туындысын тауып мына теңдіктерге келеміз (А скаляр тура мәнін білген қажет емес):
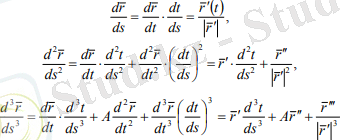(2.5)
Табылған туындылардың мәндерін негізгі формулаға қойып, қисық инварианттардың келесі есептеу формулаларын аламыз
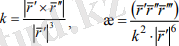(2.6)
2 Инварианттардың геометриялық мағынасы

Инвариант - бұл белгілі бір типтегі түрлендірулерде өзгеріссіз қалатын математикалық объектілердің белгілі бір класының (жиынтығының) қасиеті.
Инвариант тұжырымдамасы математикадағы ең маңыздыларының бірі болып табылады, өйткені инвариантты зерттеу белгілі бір типтегі объектілерді жіктеу міндеттерімен тікелей байланысты. Шын мәнінде, кез-келген математикалық жіктеудің мақсаты-инварианттардың кейбір толық жүйесін құру (мүмкін болса, ең қарапайым), яғни қарастырылып отырған жиынтықтан кез-келген екі балама емес объектіні бөлетін жүйені құру.
Инварианттар математиканың геометрия, топология және алгебра сияқты әртүрлі салаларында қолданылады. Инварианттардың ашылуы математикалық объектілерді жіктеу процесінде маңызды қадам болып табылады.
Мысалдар:
үшбұрыштың ауданы Евклид кеңістігінің изометрлеріне қатысты
инвариант болып табылады;
жиынның қуаты биекцияларға қатысты инвариант болып табылады.
детерминант, із, эигенвектор және матрицаның эигенверсиясы
негізді таңдауға қатысты инвариантты болып табылады;
дифференциалдық теңдеулер теориясында инвариант мәні тұрақты
(бірінші интеграл) қалаған функцияға тәуелді функция деп аталады;
Лебег өлшемі ауысуларға қатысты инвариантты;
матрицаның сингулярлық сандары ортогональды түрлендірулерге
қатысты инвариантты.
инварианттар теориясы инвариантты көпмүшелерді (немесе жай
"инварианттарды") іздеумен және алгебралық топтардың сызықтық көрсетілімдері жағдайында олар құрған алгебраны, сондай-ақ алгебралық көптүрліліктегі алгебралық топтардың әрекеттерін зерттеумен айналысады;
топологиялық инвариант - жалпы топология терминдерінің сөздігін
қараңыз;
инвариантты есептер - бұл олимпиадалық математикадағы
тапсырмалардың үлкен класы;
Хадвигер саны және хроматикалық сан - оның шыңдарын қайта
санау кезінде графиктің инварианттары.
Эллипстік қисықтың инварианты:

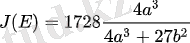
Қиғаштық инварианттың геометриялық мағынасы сызықтың қисықтығы мен бұралымының геометриялық мағынасына ұқсас анықталады.
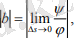(3)
Мұнда ψ - екі жақын мойын жанамалары арасындағы бұрыш, ал φ - оларға сәйкес жақын сәулелер арасындағы бұрыш.
Үлестіру параметірінің мағынасын анықтау үшін екі жақын сәулелер арасындағы қашықтығын табайық. Айқас түзулер арасындағы қашықтықты, жағдайымызға сай формуласымен есептеуге болады.
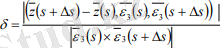(3.1)
Ɛ3(s) векторы көбейткіш ретінде аралас және векторлық көбейтінділерге кіргендіктен Ɛ3(s+ s) векторын Ɛ3(s+ s) - Ɛ3(s) векторымен алмастыруға болады. Мұның өзі шегін есептеуге мүмкіндік береді.
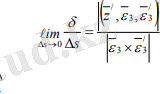(3.2)
Мұнан деривациялық формулаларын пайдаланып болатынын, атап айтқанда үйлестіру параметрінің модулі екі жақын сәуле арасындағы қашықтықтың олардың арасындағы бұрышқа қатынасының осы сәулеллердің бір-бірімен беттесуге ұмтылғандағы шешіміне тең.
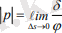(3.3)
Мойын сызығы мен сәуле араындағы бұрышыт үшін

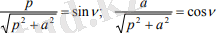
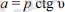
Демек а көлбеулігі р үлестіру параметрі және мойын сызығының жанамасы мен сәуле арасындағы бұрыштың катангенсіне көбейткенге тең. Егер р = 0 болса, онда
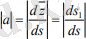(3.4)
Мұнда ds1 - мойын сызығы доға ұзындығының дифференциалы, ал ds - түзусызықты бет сфералық индикатрисасының ұзындығы дифференциалы.
2.1 Түзу сызықты бер инварианттардың есептелу формулалары

Түзусызықты бет

r = z(s) +Ɛ3 (s) (3.5)

теңдеуімен берілсін, мұнда z(s), Ɛ3 (s) инвариантты s параметірінің (сфералық индикатрисасының доға ұзындығы) функциялары. Сонда оның инварианттарына қарапайым түрде деривациялық формулаларын және
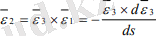(3.6)
Қатынастарын пайдалану нәтижесінде мынандай есептеу формулалары қорытылып шығарылады:

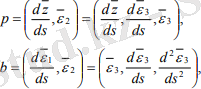
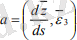(3.7)
Егер түзусызықты бет r = p(t) +l (t) теңдеуімен берілсе, мұнда p векторы кез келген бағыттаушысының радиус-векторы, l - жасушаның бағыттауышы векторы, t - кез келген параметр, онда мына формулаларды қоса қолданамыз:

ds = dƐ3 = dƐ
z = pm = p + m e
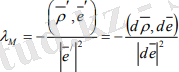(3.8)

және штрих t бойынша туынды алу белгісі. (3.7) формуласынның жалғасы ретінде төмендегі формуланы қарасырамыз:
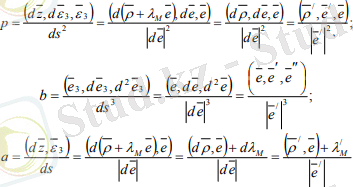(3.9)
Сонымен түзусызықты беттің кез келген t параметріне қатысты берілуіндегі есептеу формулаларының түрі:

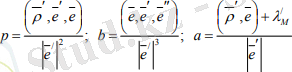
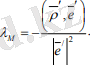(3.10)

3 Айнымалыларды ауыстыру. Инварианттары мен тензолар

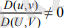(4)
шартты орындалуындағы формулаларын және қисық сызықты координаталарға көшу формулалары деп қарастыруға болады.әрине қисық сызықты координаталардың қандай да болмасын алынуында беттің қасиеттері өзгермейтіні айқын. Төменде тензорлық санау деген амалды жеңілдету мақсатында айнымалыларды жаңаша, индекс арқылы белгілейтін боламыз, атап айтқанда, u, v, U, V айнымалыларына сәйкесінше u1 , u2 , u1* , u2* әріптерімен белгілейміз.
Кейбір қозғалмайтын жүйеге қатысты алынған x, y, z декарт координаталарынан қисық сызықты u1 , u2 координаталарына көшу беттің зерттеуін жеңілдеткенмен, пайда болатын шамалардың инварианттығын қамтамасыз ете алмайды: бұл шамалар u1 , u2 айнымалыларының

ui = ui (u1* , u2*), i = 1,2,..., (4.1)

формуласы бойынша u1* , u2* айнымалыларымен алмастыру нәтижесінде беттің сол күйі сақталғанына қарамастан, өзгеруі мүмкін. Геометрия маманының алдында тұрған кокейкесті мәселе - r (u1 , u2) функциясы және оның туындылары арқылы өрнектелетін және ауыстыру нәтижесінде өзгермейтін шамаларды іздестіріп табу. Мұндай шамалар беттің инварианттары делінеді. Инварианттарды іздестіру мәселесі осыған ұқсас механика, электродинамика және векторлық анализ құралына сүйенетін түрлі пәндерде қарастырылады.
Қарапайым инварианттар геометриялық немесе физикалық мысалдардан-ақ пайда болады. Мәселен,
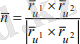(4.2)
Векторының орентацияға дейінгі дәлдәкпен инвариант екені айқын, өйткені оның ұзындығы бірге тең, ал нормаль бойындағы бағыты, әрине, параметрлер алынуына тәуелсіз.
Барлық өзге инварианттарды іздестіріп табу, ол былай тұрсын, инварианттардық толық жүйесін, атап айтқанда бетті жан-жақты анықтайтын инварианттар бумасын іздестіру әжептәуір қиындықтарға кез болады.
Дәлі оы қиындықтарды жеңу жолдары тензор ұғымының пайда болуына және тензорлық есептеудің қалыптасуына себебін тигізді.
Қазіргі күні векторлық кеңістіктің абстрактілі анықтамасына негізделген тензорлық есептеудің абстрактілі салынуы жоқ емес. Әлбетте, тензормен егжей-тегжейлі танысуды көрнекті мысалда берген қолайлы. Тензорлық бетке қатысты геометриялық фактілерге сүйеніп, екі аргументті вектор-функция негізінде енгіземіз. Сонымен, r (u1 , u2) вектор-функцияы кескіндейтін бетті оның (u1 , u2) жай нүктесі аймағында қарастырамыз. Айнымалылардың ауыстыруына тек қайтарымдылық шартымен шектейміз.
Тарау бойы латын әріпімен берілген индекстер 1 және 2 мәндерін қабылдайды деп санаймыз. Тензорлық санағы үшін келесі ықшам белгілерін енгізген ыңғайлы
(4.3)
Екі матрицалар өзара кері матрица болғандықтан,
(4.4)
болатыны айқын. Мұндағы ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.