Сфералық қозғалыстағы қатты дене нүктелерінің жылдамдығы

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

Мазмұны

Кіріспе

: 1

Кіріспе: Сфералық қозғалыс

3: 4

: 1. 1

Кіріспе: Сызық ұғымы

3: 6

: 1. 2

Кіріспе: Эйлер сипаттамасы

3: 8

: 2

Кіріспе: Эйлер бұрыштары

3: 14

: 2. 1

Кіріспе: Эйлер-Даламбер теориялары

3: 16

: 2. 2

Кіріспе: Қатты дененің еркін қозғалысы

3: 18

: 2. 3

Кіріспе: Дюпен индикатриясы

3: 18

Кіріспе: Қорытынды

3: 20

Кіріспе: Пайдаланған әдебиетттер тізімі

3: 21

Кіріспе

Курстық жұмыстың өзектілігі : бұл жұмыстың мақсаты студенттерге табиғаттың негізгі заңдылықтарын оқыту; табиғаттағы және техникадағы болып жатқан құбылыстардың математикалық модельін құру және қазіргі заманғы математиканың құралдарын және әдістерін пайдалана отырып талдау жасауға дағдыландыру; болашақ мамандардың ғылыми жалпылау және қорытынды жасау қабілеттерін дамыту.

Курстық жұмыстың мақсаты :

Эйлер бұрыштарын толықтай талқылау;
Эйлер бұрыштарын есептерді шығару барысында көрсету;
есептерді шешудің негізгі әдістерін және қабылдауларын оқыту;
есептерді шешуде орнықты дағдыға ие болу.

Дифференциалдық геометрияның өзге геометриялық пәндер ішінен бөлінуі - зерттеу аймағы емес, зерттеу тәсіліне немесе дәлірек айтса, зерттеу аппараттарына байланысты деуге болады. Аналитикалық геометрияның бүгінгі таңдағы мазмұндалуы векторлық алгебра аппаратынсыз мүмкін болмауына ұқсас дифференциалдық геометрия да векторлық анализ - демек мәндері немесе аргументтер жиыны векторлар болып келетін функциялар теориясыннсыз мүмкін емес.

Функциялар теориясында көңіл негізінен инварианттардышығарып алуға, атап айтқанда скаляр аргументін ауыстыруға тәуелсіз немесе векторлық аргумент жағдайында векторлық базисті ауыстыруға тәуелсіз шамаларды алуға аударылады. Бұл бағытта беттер теориясы және өріс теориясының негізгі фактілері оп-оңай алынып, соынмен бірге тензор ұғымының пайда болуы орынды.

Геометрия, механика және математика ғылымдарынң дамуына үлес қосқан, XVIII ғасырдың үлкен ғұламаларының бірі Леонид Эйлер жайлы айта кеткен жөн. Осы күнгі көптеген геометриялық мәселелер мен идеяларға деген көзқарастың өзгеше болуының арқасында, Эйлер бұрыштарын әлемге талқылаған. Курстық жұмыстың негізгі тақырыбы Эйлер бұрыштары жайлы.

Курстық жұмыстың құрылымы : жұмыс кіріспеден, жеті бөлімнен, қорытындыдан, пайдаланылған әдебиеттер тізімінен және 21 беттен тұрады.

Сфералық қозғалыс

Сфералық қозғалыс (қозғалмайтын нүктенің айналасындағы қатты

дененің қозғалысы) - бір қозғалмайтын нүктесі бар абсолютті қатты дененің қозғалысы (1-сурет) .

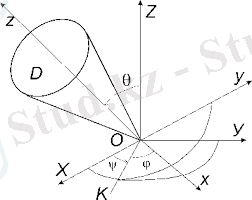
$C:\Users\Admin\Downloads\Без названия.png$

1-сурет - Сфералық қозғалыс

Тұрақты О нүктесінің айналасында қозғалғанда, қатты дененің әр нүктесі кеңістіктегі сфералық бетті сипаттайды, оның орталығы О нүктесі болып табылады.

Сфералық қозғалыс заңдылықтарын сипаттау кезінде Эйлер бұрыштары деп аталатын координаттарды қолданамыз.

1) φ = f ₁ (t) - меншікті айналу бұрышы;

2) ψ = f ₂ (t) - прецессия бұрышы;

3) Ө = f ₃ (t) - тербелу бұрышы;

4) N түйіндерінің сызығы - ху координаталық жазықтықтарының қиылысуы.

Сфералық қозғалыстың мысалы - прецессия шыңының немесе инерцияның ең кіші немесе ең үлкен моментінің осіне сәйкес келмейтін осьтің айналасында бұралған кез-келген дененің қозғалысы. Тағы бір мысал - тісті конустық планетарлық берілістегі конустық роликтің тістеріндегі нүктелердің қозғалысы. Сфералық қозғалыс сипаттамаларының бірі апекс қозғалысымен байланысты, оның траекториясы бірлік сферада, атап айтқанда гироскоптардың динамикасында зерттеледі.

Апекс (механикада) - координатаның басында центрі бар бірлік сферадағы нүкте, ол абсолютті қатты дененің динамикалық симметриясының осі бойымен қозғалмайтын нүктемен (мысалы, гироскоп) бағытталған бірлік векторының ұшы болып табылады. Апекстің бірлік сферадағы қозғалысы қатты дененің динамикалық симметриясының осінің қозғалысын, яғни прецессия мен нутацияны толық сипаттайды.

APB және A ₁ PB ₁ сфералық үшбұрыштары үш жағынан тең және оларды бекітілген О нүктесі мен Р нүктесі арқылы тартылған осьтің айналасында бұру арқылы біріктіруге болады. ОР осі соңғы айналу осі деп аталады (1. 1-сурет) .

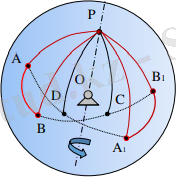
$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

1. 1-сурет - Айналу осі

Ось біріншісіне шексіз жақын, оны денені бір жерден екінші жерге ауыстыру үшін айналдыру керек, оны жылдам айналу осі деп атайды (1. 4-сурет) .

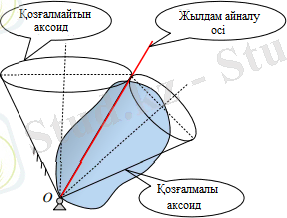
$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

1. 3-сурет - Аксоидтардың түрлері

Бекітілген нүктенің айналасындағы кез-келген қозғалысты лездік осьтер жиынтығының айналу тізбегімен алмастыруға болады.

Қозғалмайтын осьтерге қатысты лездік осьтердің геометриялық орны қозғалмайтын аксоид деп аталады. Қозғалмайтын аксоид - дененің қозғалмайтын нүктесінде шыңы бар конустық бет. Қозғалатын денеде лездік айналу осьтерінің геометриялық орны қозғалмалы аксоид деп аталады. Қозғалмайтын аксоид сияқты, қозғалмалы аксоид - бұл қозғалмайтын нүктеде шыңы бар конустық бет (1. 3-сурет) .

Қатты дененің айналуымен байланысты қозғалмалы аксоид қозғалмайтын аксоид арқылы сырғып кетпейді және олардың жалпы түзілуі әр сәтте дененің айналу осі болып табылады.

Сфералық қозғалыстағы қатты дененің бұрыштық жылдамдығы. Сфералық қозғалыстағы қатты дененің лездік бұрыштық жылдамдығы-айналу осі бойымен бағытталған вектор, оның соңынан дененің айналуы сағат тіліне қарсы бағытта көрінеді, оның модулі:

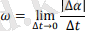$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$ (1)

Лездік бұрыштық жылдамдық ω құрамдас қозғалыстардың бұрыштық жылдамдықтарының векторлық қосындысына тең:

ω = φK + ψk + Өn (1. 1)

Ось бұл қатты дененің қозғалмайтын О нүктенің айналасында жылдам айналу осі, ω векторымен сәйкес келетін.

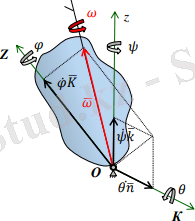
$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

1. 4-сурет - Жылдам айналу осі

Сфералық қозғалыстағы қатты дене нүктелерінің жылдамдығы. Бекітілген нүктенің айналасында айналу кезіндегі дене нүктелерінің сызықтық жылдамдығын Эйлер формуласы бойынша есептеуге болады, өйткені бекітілген осьтің айналасында айналу жағдайында әр нүктенің радиус-векторын бекітілген нүктеден жүргізу ыңғайлы:

v = ω ^. r (1. 3)

Жылдамдық модулі v = ωrsinα = ωh, мұндағы h қарастырылған нүктеден лезде айналу осіне дейінгі ең қысқа қашықтық.

Осылайша, сфералық қозғалыстағы дене нүктелерінің жылдамдығы сол нүктелерден лездік оське дейінгі қашықтыққа пропорционал.

1. 1 Сызық ұғымы

Аналитикалық геометрияда сызықты анықтайтын функцияларға дифференциалдау шарты қойылмағандықтан, ондағы сызық анықтамасы дифференциалдық-геометриялық зерттеу негізінде жата алмайды. Сол себептен де сызықтың шынайы топологиялық анықтамасы да айтқан зерттеуде қолайсыз.

Біздің енгізетініміз - сөз етккен зерттеулерге ыңғайлы және өзге анықтамаларға қайшы келмейтін сызық ұғымы анықтамасы. Атап айтқанда енгізілетін сызықтар аналитикакалық геометриядағы және топологиядағы сызықтарды қамтиды.

А - кез келген нүктелер жиыны, Д - түзу кесіндінің нүктелер жиыны болсын. А және Д нүктелері араында өзара бірмәнді сәйкестік орнығып, бұл сәйкестік ең болмағанда бір декарт координаталар жүйесінде жеткілікті рет дифференциалданатын екі функциямен бірлесе, А жиынын сызықтың қарапайым үзігі дейміз.

Егер түзу ретінде ОХ осі алынса, онда қарапайым үзік

$у = \varphi(х)$ , $\ \ z = \text{ψ}(х)$ , (1. 4)

теңдеулерімен беріледі, мұнда $\varphi$ және $\text{ψ}$ кейбір D $\epsilon$ O _x кесіндісінің барлық нүктелерінде дифференциалданатын функциялар.

Енді жеткілікті рет дифференциалданатын бір айналымға тәуелді

$r = r(t)$ , (1. 5)

Вектор функция келбетін қарастырайық. Бұл функцияның берілуі r векторының координаталары болып келетін

x = f ₁ (t), y = f ₂ (t), z = f ₃ (t) (1. 6)

скаляр функцияларының беріліуіне эквивалент.

Анализден мындай жәйт мәлім - y - y (х) теңдеуін (y (х) - ) M(х, y) нүктесі аймағындах-ке қатысты шешу үшін, М нүктесінде

y ^/ (х) ≠0 (1. 7)

болу керек. Сонда х=x(y) шешімі де М нүктесінің кейбір маңында дифференциалданатын функция болып келеді.

Егер берілген t мәнінде f _i (t) туындыларының бірі нөлден өзгеше болса, онда (1. 3) -тің сәйкес теңдеуін t -ға қатысты шешеміз.

y = f ₂ (t(x) ), z = f ₃ (t(x) ) (1. 8)

Кеңістік сызығы (немесе қисығы) деп бір аргументті жеткілікті рет дифференциалданатын $r = r(t)$ вектор-функция келбетін айтамыз. $r \neq \ r(t)$ орындалатын нүктелер қисықтың жай нүктелері, $r = r(t)$ болатын нүктелер қисықтың ерекше нүктелері делінеді.

Геометриялық тұрғыда $r(t) \neq \ \ 0$ шарты сызықтың жанамасын қамтамасыз етеді. Сонымен сызықтың жай нүктесінде әрқашан білгілі жанама бар.

Ескерту. $r(t) \neq \ \ 0$ шарты сызық нүктесі аймағын қарапайым үзік ретінде келтірудің жеткілікті шарты болып келеді, жалпы алғанда ол қажетті шарт болуы міндетті емес. Дербес жағдайда r ^/ -тың нөлге айналуы t айнымалсын ауыстыру нәтежесі болуы мүмкін. Мәселен, t= $\tau^{3}$ арқылы жаңа $\tau$ айнымалысына көшсек.

r _t = r ^/ (t( $\tau$ ) ) = 3 $\tau$ ² r _t (1. 9)

Эйлер сипаттамасы

Леонард Эйлер - швейцариялық математик, механик және физик. Базель университетін бітірген. 1727 жылдан Санкт-Петербург академиясында қызмет істеді. Ол - Санкт-Петербург және Берлин академияларынан басқа Париж академиясының, Лондон корольдық қоғамының, Санкт-Петербург академиясының, т. б. көптеген ірі ғыл. қоғамдардың мүшесі болды. Эйлердің негізгі еңбектері сол кездегі математика мен механиканың барлық саласына, серпімділік теориясына, математикалық физикаға, оптикаға, музыка теориясына, машиналар теориясына, баллистикаға, теңіз ғылымына, т. б. арналған.

Оның ғылыми еңбектерінің жинағы ауқымды 60-80 том көлемінде деп болжанады. Эйлер «Аналитикалық түрде баяндалған механика не қозғалыс туралы ғылым» (2 томдық, 1736), «Анализге кіріспе» (2 томдық, 1748), «Дифференциалдық есептеу» (1755), «Универсал арифметика» (2 томдық, 1768 - 1769) және 6 тілде 30 шақты рет басылып шыққан «Интегралдық есептеу» (3 томдық, 1768-1770; 4 томдық, 1794), т. б. осы сияқты бірқатар монографияларында өзінің және басқа ғалымдардың зерттеулерінің нәтижелерін жүйеге келтірді.

Ол «Механика» атты монографиясында жаңа математикалық анализдің көмегі арқылы нүкте динамикасын тұңғыш рет кең көлемде баяндады, ал «Қатты денелер қозғалысы теориясында» қатты дененің кинематикасы мен динамикасының теориясын жетілдірді және қатты дененің қозғалмайтын нүкте маңынан айналу теңдеуін (гироскоптар теориясының бастамасы болған) тапты. Аспан механикасы бойынша да үлкен жаңалықтар ашты. 1757 - 1771 жылдары жарық көрген мемуарлары тұтас орта механикасы жөнінен жүргізілген зерттеулерге қосылған елеулі үлесі болды. Эйлер вариациялық есептеу мен дифференциалдық теңдеулер теориясының негізін жасады, дифференциалдық және интегралдық есептеулерді жалпылап, одан әрі дамытты. Ол - 886 мақала мен мемуардың авторы.

Шеті бар екіөлшемді көпбейнеліктердің торкөзді бөл шектенуі. Кескіндіге гомеоморфты бейне жай доға, ал шеңберге гомеоморфты бейне жай тұйық қисық немес бірөлшемді цикл делінеді (1. 5-сурет) .

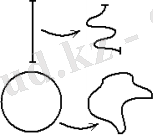
$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

1. 5-сурет - Гомеоморфты бейне

W - конпактылы, шеті бар екіөлшемді көпбейнелік болсын. Онда егер оның дW шеті бос болмаса, оның әрбір компонентасы тұйық қисық және мұндай компоненталар саны шектеулі болады.

W- дегі ∑ торкөзі деп шектеулі саны бар А ₁ , . . . , А _т нүктелері және ұштары осы нүктелерде орналасқан, әрі ішкі нүктелерінде бірімен бірі қиылыспайтын шектеулі саны бар ɣ ₁ , . . . , ɣ _п жай доғаларының кез келген бумасын айтатын боламыз. А ₁ , . . . , А _т нүктелері торкөздің төбелеріғ ал ɣ ₁ , . . . , ɣ _п доғалары торкөздің қырлары делінеді.

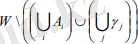$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$ (2)

Жиын компоненталарын ∑ торкөзінің обылстары дейтін боламыз. Егер ∑ торкөзінің әрбір облысы ашық дөңгелекке гомеморфты болса, онда ∑ торкөзі шеті бар W көпбейнелігінің торкөзді бөлшектенуін береді дейді. Мұндайда торкөз төбелері торкөзді бөлшектенудің нөлөлшемді торкөзшелері, ұштары жоқ торкөз қырлары - бірөлшемді торкөзшелер, ал торкөз облыстары - екіөлшемді торкөзшелер делінеді. Торкөз және торкөзді бөлшектенудің мысалдарын келтірейік.

Жалғыз А нүктесінен тұратын S ² сферасындағы торкөз бір нөлөлшемді және бір екіөлшемді торкөзшеден тұратын сфераның торкөзді бөлшектенуін береді (1. 6-сурет) .

$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

1. 6-сурет - Сфера

Параллель және меридиан екіөлшемді Т ² торын, параллель және меридиананның қиылысу нүктесі болып келетін бір нөлөлшемді торкөзше мен, екі бірөлшемді және бір екіөлшемді төркөзшелерге бөлшектенеді (1. 7-сурет) .

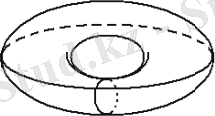
$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

1. 7-сурет - Сфералық жазықтық

Эйлер сипаттамасының анықталуы. Әрбір шеті бар W екіөлшемді көпбейнелік торкөзді бөлшектенуді мүмкін ететін дәлелдеуге болады. Егер W - компакттылы болса, онда оның кез келген торкөзді ∑ бөлшектенуінде әрбір өлшемділіктігі торкөзшелер саны шектеулі. α _і арқылы і- өлшемді торкөзшелер санын белгілейік, мұнда і = 0, 1, 2.

Х(W) =α ₀ - α ₁ + α ₂ (2. 1)

Саны, шеті бар екіөлшемді компактылы W көпбейнелігінің Эйлер сипаттамасы делінеді.

Эйлер сипаттамасы анықтамасының корректілігін, атап айтқанда Х(W) - ның торкөзді бөлшектеуіне тәуелсіздігін дәлелдеуге болады. Төменде мұндай дәлелдемені S ² сферасы үшін жүргіземіз. Әзірше, алдыңғы бапта қарастырылған, шеті бар екіөлшемді көпбейнеліктер үшін саналған Эйлер сипаттамаларын келтірейік. Осы мақсатпен салынған төркөзді бөлшектенулерді барынша пайдаланамыз.

S2сферасы; α0=1; α1=0; α2=1; Х(S2) = 1+1= 2
Т2торы; α0=1; α1=2; α2=1; Х(Т2) = 1-2+1= 0
Р2проективтік жазықтығы; α0=1; α1=1; α2=1; Х(Р2) = 1-1+1= 1
М2Мебиус жапырағы; α0=1; α1=2; α2=1; Х(М2) = 1-2+1= 0
D2дөңгелегіS1шеңбері болып келген дөңгелек шекарасында кез

келген А нүктесін аламыз. Бұл нөлөлшемді А торкөзшесін, бір бірөлшемді S ¹ /А торкөзшесін және бір екіөлшемді D ² / S ¹ торкөзшесін қамтитын D ² -ның торкөзді бөлшектенуін аламыз. Сондықтан α ₀ = α ₁ = α ₂ = 1 және Х(D ² ) = 1-1+1= 1.

Эйлер сипаттамасының қосылымдылығы. Эйлер сипаттамасының маңызды қосылымдылық қасиеті бар.

W ₁ , . . . , W _s - шеті бар компактылы көпбейнеліктер және φ ₁ , . . . , φ _r бейнелеулері дW ₁ , . . . , дW _s шеттерінің кейбір компоненттері жұптарының арасындағы гомеоморфизмдер, оның үстіне әрбір компонента бірден бір жұпқа кіретіндей болсын. Егер шеті бар W көпбейнелігі W ₁ , . . . , W _s көпбейнеліктерінен φ ₁ , . . . , φ _r бейнелеулері бойынша желімдеуден алынса, онда

Х(W) = Х(W ₁ ) + . . . + Х(W _s ) (2. 2)

Дәлелдеме. Ең алдымен байқайтынымыз, кез келген бірөлшемді торкөзше ішіндегі торкөзді бөлшектенуге нөлөлшемді торкөзше тіркелгеннен, қайта торкөзді бөлшектену аламыз. (2. 1) қосындысы мұндайда өзгермейді, өйткені әрбір осындай қосылғыш бірөлшемді торкөзшелер санын да бірге арттырады.

Сондықтан φ ₁ , . . . , φ _r гомеоморфизмдері әрбір нөлөлшемді торкөзшені нөлөлшемді торкөзшемен, бірөлшемді торкөзшені бірөлшемді торкөзшемен желімдейтіндей, W ₁ , . . . , W _s шеттері бар ∑ ₁ , . . . , ∑ _s торкөзді болшектенулер салынған деп есептеуге болады. Осы торкөзді ∑ ₁ бөлшектемелері W- де ∑ торкөзді болшектенуді анықтайды. α _і ^j - ∑ ₁ (∑) болшектенуіндегі і -өлшемді ( і = 0, 1, 2) торкөзшелер саны болсын. Тұйық көпбұрыш қабырғаларының саны оның тобелерінің санына тең болғандықтан, бірөлшемді циклдарды желімдегенде, нөлөлшемді торкөзшелер саны желімдеген соң қандай шамаға кемитін болса, бірөлшемді торкөзшелер саны да сондай шамаға кемиді. Сондықтан

α ₀ ¹ + . . . + α ₀ ^s - α ₀ = α ₁ ¹ + . . . +α ₁ ^s - α ₁ (2. 3)

α ₂ ¹ + . . . + α ₂ ^s = α ₂ (2. 4)

(2. 3) және (2. 4) тендіктерінен (2. 2) теңдігі туындайды.

1-салдар. S ² сферасынан, ашық дөңгелекке гомеоморфты, қиылыспайтын Q ₁ , …, Q _p обылстарын алып тастағаннан шыққан шеті бар S _р ² ( р - тесігі бар сфера) көпбейнелігінің Эйлер сипаттамасы 2 - р -ға тең.

2-салдар. Тұтқаның Эйлер сипаттамасы - 1-ге тең.

(2. 1) теңдігіндегі қосындының S ² сферасына жасалған торкөздік бөлшектеуді алудан тәуелсіздігінің дәлелдемесі К. Жорданның келесі теоремасына негізделген.

Теорема. Сферадағы кез келген цикл оны екі облысқа бөліп, олардың ортақ шекарасы болып табылады.

Сферадағы торкөз үшін жасалған Эйлер теоремасының төмендегідей жалпыламасы бар.

Теорема. ∑ - S ² сферасындағы торкөз, α ₀ - торкөз төбелерінің саны, α ₁ - қырлар саны, α ₂ - торкөз облыстар саны және l - онаң байламды компоненталар саны. Сонда

α ₀ - α _{1 +} α ₂ - l= 1 (2. 5)

Дәлелдеме. Ең алдымен байқайтынымыз, ∑ ₀ бос торкөзі үшін (2. 5) формуласы орындалады, өйткені осы жағдайда α ₀ = α ₁ =l= 1, ал α ₂ = 1 . Енді кез келген ∑ торкөзінен, төбелері мен қырларын біртіндеп алып тастай отырып және алған сайын λ( ∑) =α ₀ - α _{1 +} α ₂ - l өрнегінің өзгермейтіндігін тексере келе, ∑ ₀ бос торкөзіне көшеміз. Соңғы сәтте бос торкөз үшін λ( ∑ ₀ ) =1 болғандықтан, онда бастапқы торкөз үшін де λ( ∑) =1 болады. Теорема дәлелдемесінің мәнісі де осында. Осы амалдарды сипаттап шығайық.

∑/торкөзі∑-дан торкөздің оқшау тобесін алып тастағаннан шығады. Ондаα0жәнеlсандарының әрқайысы бірге кемиді, алα1менα2өзгермейді. Сондықтан λ(∑0) =λ(∑)
Оқшауланған төбелердің бәрі алынып тасталған деп санап, ∑торкөзі, бос ұшы болып келген бір ғанаɣjқыры тірелгенАітөбесіне ие болады деп ұйғарайық (1. 8-сурет) . ОсыАітөбесі менɣjқырын алып тастап, бірақɣjқырының екінші ұшын қалдырғаннан∑/торкөзін шығарып аламыз. Ол торкөз үшінα0жәнеα1мәндері 1-ге кемиді, алα2менlөзгермейді. Сондақтан λ(∑/) =λ(∑) .
Бірінші және екінші амалды тізбекті қолданғаннан, оқшауланған төбелері және бос ұштары болмайтын∑торкөзіне келеміз. Егер бұл торкөз бос болмаса, онда оның қырларынан кем дегенде бірδциклын құрастыруға болады (1. 9-сурет) . Жоғарыда айтылған теоремаларға сәйкес, ос цикл құрамына кіретін әрбірɣjқыры∑торкөзінің түрлі екі облсының шекарасында жатады.

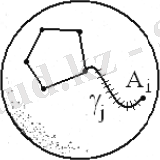
$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

1. 8-сурет - Сфера мен торкөз

Сондықтан ɣ _j ұштарын емес, өзін алып тастағаннан ∑ торкөзінен ∑ ^/ торкөзіне ауысамыз; оның α ₁ мен α ₂ шамалары 1-ге кемігеннен, α ₀ мен l сандары өзгермейді. Сондықтан, тағы да λ( ∑ ^/ ) = λ( ∑) .

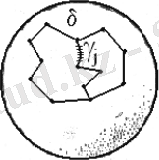
$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

1. 9-сурет - Сфера мен торкөз қырлары

S ² сферасының торкөздік бөлшектенуін анықтайтын ∑ торкөзінің әрбір облысы ашық дөңгелекке гомеоморфты болғандықтан, мұндай торкөз үшін l= 1, өйткені мұндай торкөз бір ғана компонентаны қамтиды. Сфераның кез келген торкөздік бөлшектенуі үшін

α ₀ - α _{1 +} α ₂ = 2 (2. 6)

теңдігі орындалатыны, атап айтқанда Эйлер сипаттамасы корректілі анықталатыны туындайды. S ² сферасына гомеоморфты кез келген тұйық Р көпжағы үшін, оның төбелері, қырлары мен жақтарының бумасы көпжақтың торкөздік бөлшектенуін беретінін қосымша айта кеткен жөн. Сондықтан (2. 6) теңдігінде α ₀ Р- ның төбелері санын, α ₁ - оның қырларының санын, ал α ₂ - жақтары санын білдіреді. Осының өзі көпжақтар үшін кескінделген әйгілі Эйлер теоремасының мазмұнын құрайды.

2 Эйлер бұрыштары

Эйлер бұрыштары жүйенің кез-келген орнын ағымдағы күйге келтіруге мүмкіндік беретін жүйенің үш бұрылысын анықтайды. Бастапқы координаталар жүйесін ( x, y, z ), соңғыларын ( X, Y, Z ) деп белгілейміз. XY және ху координаталық жазықтықтарының қиылысы N түйін сызығы деп аталады (2-сурет) .

1) φ = f ₁ (t) - меншікті айналу бұрышы;

2) ψ = f ₂ (t) - прецессия бұрышы;

3) Ө = f ₃ (t) - тербелу бұрышы;

4) N түйіндерінің сызығы - ху координаталық жазықтықтарының қиылысуы.

Жүйенің осы бұрыштардағы бұрылыстары деп аталады баяу қозғалыс, тербелістер және өз бұрышына бұрылу (айналу) . Мұндай бұрылыстар коммутативті емес және жүйенің соңғы позициясы бұрылыстардың тәртібіне байланысты.

Эйлер бұрыштары жағдайында алдымен Z осінің айналасындағы α бұрышына, содан кейін N осінің айналасындағы β бұрышына, ал соңғысы z осінің айналасындағы ɣ бұрышына айналады.

Эйлер бұрыштары айналмалы координаттар жүйесінің осьтерінің айналасындағы пассивті бұрылыстардың дәйекті комбинациясын сипаттайды. Бұл бұрылыстардың матрицалары келесідей:

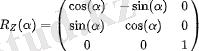
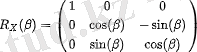
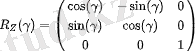$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$ (3)

Осы бұрылыстардың дәйекті орындалуы мынандай матрицаны береді:

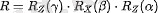$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$ (3. 1)

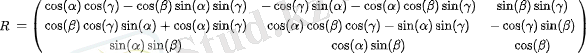
$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

R ^. (x, y, z) көбейтіндісі, мұндағы x, y, z- бұрылысқа дейінгі нүктенің координаталары, айналғаннан кейін қозғалмалы координаттар жүйесіндегі нүктенің координаталарын береді. Айналғанға дейін және кейін жылжымалы координаттар жүйесіндегі нүктенің координаттары өзгермейді.

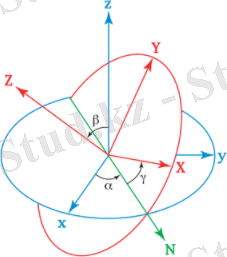
$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

2-сурет - Эйлер бұрыштары

Эйлер кинематикалық теңдеулері.

ω = φK + ψk + Өn векторының проекцияын аламыз, жылжымалы ОХУZ координаттар жүйесінің осінде.

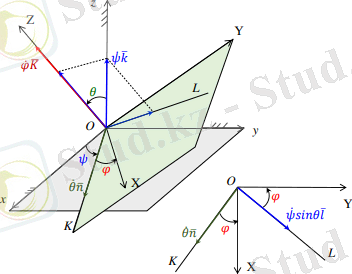
$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$

2. 1-сурет - Кинематикалық теңдеуге қосымша

Прецессияның бұрыштық жылдамдығының векторын OZ осі бойымен екі өзара перпендикуляр компоненттерге және OK түйіндерінің сызығына перпендикуляр OL көмекші осіне алдын-ала таратамыз (2. 1-сурет) . Cонда:

ω _х = ψsinӨsinφ + Өcosφ;

ω _у = ψsinӨcosφ - Өsinφ;

ω _z = φ + φcosӨ.

Бұл теңдеулік арақатынастар Эйлер кинематикалық теңдеулері деп аталады.

2. 1 Эйлер-Даламбер теориялары

Эйлер-Даламбер теориясының маңызы мынада: тұрақты О нүктесі бар қатты дененің ең көп таралған соңғы қозғалысы осы нүктеден өтетін тұрақты осьтің айналуы.

AB = A ₁ B ₁ (қатты дененің нүктелері арасындағы қашықтық) .

AD = DA ₁ , BC = CB ₁

D және C нүктелерінде Р нүктесінде қиылысатын АA ₁ және BB ₁ доғаларына сфералық перпендикулярларды тартамыз.

АР = А ₁ Р, ВР = В ₁ Р тең проекциясы бар доғалар сияқты қабылдаймыз (1. 1-сурет) .

2. 2 Қатты дененің еркін қозғалысы

Бекітілген нүктенің айналасында айналу кезіндегі дене нүктелерінің сызықтық жылдамдығын Эйлер формуласы бойынша есептеуге болады, өйткені қозғалмайтын осьтің айналасында айналу жағдайында тек әр нүктенің радиус-векторы қозғалмайтын нүктеден өткізуге ыңғайлы.

v = r ^. ω (3. 2)

Жылдамдық модулі v = ωrsinα = ωh, h қарастырылған нүктеден жылдам айналу осіне дейінгі ең қысқа қашықтық. Осылайша, сфералық қозғалыстағы дене нүктелерінің жылдамдығы сол нүктелерден лездік оське дейінгі қашықтыққа пропорционал.

Эйлер формуласының оң жағын анықтаушы ретінде қарастырайық:

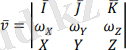$C:\Users\Admin\Desktop\Новый точечный рисунок.bmp$ (3. 3)