Негізгі реологиялық механикалық модельдері

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Қазақстан Республикасы Білім және Ғылым министрлігі М. Әуезов атындағы Оңтүстік Қазақстан университеті

Реферат

Тақырыбы: Негізгі реологиялық механикалық модельдері

Орындаған: Керімбай М

Тобы:ЖТ-19-2К4

Қабылдаған: Желеуова Ж

Жоспар

Реология жайлы жалпы түсінік

Элементарлық реологиялық моделдердi сипаты

Құрылымдық жүйелердің негізгі ығысулық қасиеттері

Қолданылған әдебиеттер

Негізгі реологиялық механикалық модельдері.

Реология - материалдардың деформациялық қасиеттері туралы ғылым. Ол механиканың, термодинамиканың және геометрияның әмбебап қағидалары негізінде кез келген материалдар үшін орындалатын және жалпылама деформациялаушы күштер әсерінен олардың өзгеру заңдарын орнататын тұтас орта механикасынан (ТОМ) кейбір негізгі түсініктерді алған. Материалдар реологиялық объектілер ретінде серпімділікпен, тұтқырлықпен, беріктікпен және басқа реологиялық тұрақтылармен сипатталады. Реологияның негізгі міндеттерінің бірі белгілі бір рецептура және технология бойынша дайындалған материал қандай зат: серпімді қатты зат, аққыш сұйықтық, эластикалық (каучук тәріздес) дене, пластикалық құрам немесе басқа нәрсе болып шығатынын және рецептура мен технология реологиялық күй мен тұрақтылар шамаларына қалай әсер ететінін орнату болып табылады. Бұл мәселені шешудің негізгі жолы - эмпирикалы, яғни материал салмақ түскенде қалай өзгеретінін тәжірибелік жолмен орнату. Реология заңдарын танудың осы жолы зерттелетін, бұл жағдайда реологиялық, объектілер мен құбылыстарды жіктеугеәкеледі. Әртүрлі материалдарды күнделікті пайдалану тәжірибесі оларды қатты, сұйық және газ тәріздес деп бөлуге мүмкіндік береді. Әрбір топ сыртқы күштердің әсерінен өзіне тән қасиеттерді көрсетеді, сондай ақ деформациялау режиміне (жылдамдығына) қарай басқа топтың қасиеттерін де көрсете алады. Мысалға, батыру жағдайына қарай сұйық заттың қасиеттерін (өз салмағының әлсіз ұза әсер етуші күшінен қалқып шығады) қатты дененің қасиеттерін (балғамен ұрғанда сынады) көрсетеді, сондай ақ шамасы бойынша қалыпты импульс күші қысқа уақытқа әсер еткенде серпімділік пайда бола алады. Барлық материалдар қандай да бір деңгейде битумға ұқсас, ал дисперсті жүйелер басқа да күрделірек реологиялық қасиеттерді анықтайды. Материалдардың құрылымдық-механикалық қасиеттерінің деформациялау режиміне және жүйе параметрлеріне тәуелділіктерін толық зерттеумен инженерлік реология айналысады. Инженерлік реологияның негізгі міндеті зерттеу объектісінің өзгеру заңдарын анықтау, реологиялық модельді таңдау және негізгі реологиялық тұрақтыларды анықтау.

Қарапайым реологиялық денелердің келесі механикалық моделдері белгілі: Ньютон моделі, Гук моделі, Сен-Венан моделі, Рэнкин моделi және Пелег моделі.

Ньютон моделі демпфер (сурет 4. 1, а ), немесе тұтқыр сұйықтың моделі болып табылады. Бұған сәйкес математикалық модель қарапайым ығысудағы реологиялық тұрақты - тұтқырлық үшін ньютондық дене күйінің реологиялық теңдеуі болып табылады. Бұған сәйкес математикалық модель ньютондық дененiң қарапайым ығысқан кезiндегi күйiнiң реологиялық теңдеуi болып табылады, реологиялық тұрақты - тұтқырлық .

Гук моделi болып серiппе (сурет 1. 1, б ) немесе серпiмдi қатты дене моделi болып табылады. Бұған сәйкес математикалық модель гуктық қатты дененiң қарапайым ығысқан кезiндегi ( созылу мен сығылу кезiндегi ) күйiнiң реологиялық теңдеуi болып, ал реологиялық тұрақты - ығысу модулi G болып табылады.

Сен-Венан моделi екi үйкелiс түрiнде бейнеленiп, нақты пластикалық дене моделi ретiнде сипатталады (сурет 1. 1, в ) . Ағу шегiнен аз жүктеу кезiнде ол ешқандай қозғалыссыз, ал одан асқанда шексiз деформацияланады. Ағу шегi пластикалық элементтiң реологиялық тұрақтысы болып табылады.

Тамақ өнiмдерiнiң құрылымдық-механикалық қасиеттерiн меңгеруде олардың лездiк қалпына келмейтiн деформациялары кезiндегi бүлiнуiн тексередi.

Рэнкин моделi немесе қатты дене моделi екi iлiнiскен пластиналар жұбы түрiнде бейнеленедi (сурет 1. 1, г ) . Бұл элемент үшiн реологиялық тұрақты берiктiк шегi ( ) болып табылады. . Егер өстiк жүктелу шамасы берiктiк шегiнен асып кетсе, онда iлiнiскен пластиналар ажырайды.

Лездiк қайтып қалпына келмейтiн деформацияларды Пелег моделi немесе қатты дене моделi ескере алады. Пелег моделiн (сурет 1. 1, д ) жүктеу кезiнде 0-дiк шекке дейiн деформацияланады, ал түйiсу жүзеге асқаннан кейiн өзiн қатты дене ретiнде ұстайды

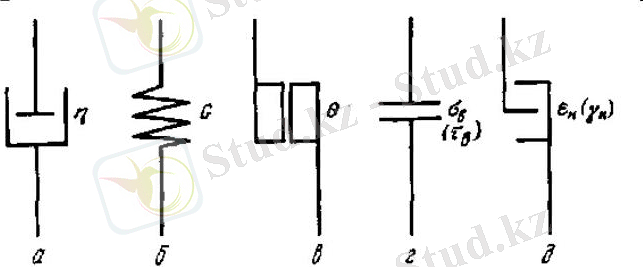Сурет 4. 1. Элементарлық реологиялық моделдердi сипаттайтын

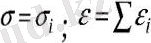механикалық моделдер:

а - Ньютон моделi; б - Гук моделi; в - Сен-Венан моделi; г - Рэнкин моделi; д - Пелег моделi.
Тiзбектелiп қосылуда барлық денелердiң кернеуi бiрдей болады, ал олардың деформациялары қосылады

Параллель қосылуда барлық денелердiң деформациялануы бiрдей, ал моделдiң жалпы моделi жекеленген денелердiң кернеуiнен құралады

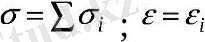
Элементарлы моделдi денелер үшiн кернеу мен деформацияның уақыт бойынша туындысын қосқан дұрыс болады.

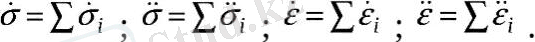
2. Элементарлы және күрделi моделдi денелердiң бiросьтiк кернеулiк жағдайындағы деформациялық күйi келесi дифференциалды теңдеумен сипатталады:

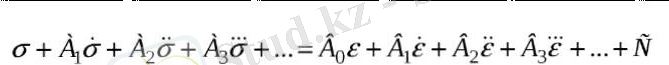
Теңдеудiң сол жағында кернеу және оның уақыт бойынша туындылары, және, сонымен қатар материал тұрақтылары орналасады. Оң жағында деформация , оның тұрақтылары, және, сонымен қатар материал тұрақтылары В ₀ , В ₁ , В ₂ , В ₃ , … және коэффициент С. Элементарлы модельдi денелердiң бiр ғана тұрақтысы болады.

Гуктың серпiмдi элементi мен Сен-Венанның (сурет 4. 2) пластикалық элементiн тiзбектеп қосқан жағдайда серпiмдi-пластикалық дене моделi алынады. болған кезде материалдың серпiмдi деформациялануы, ал - пластикалық ағуы жүзеге асады.
диаграммасы. γ-θ

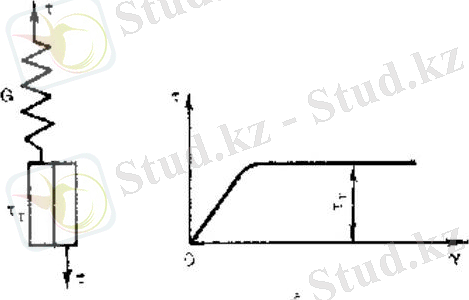
Сурет 1. 2. Серпiмдi-пластикалық денесінің моделi және

Кельвин-Фойгттың тұтқыр-пластикалық денесi Гуктың серпiмдi элементiмен ньютонның тұтқыр элементiн параллель қосқанда алынған механикалық модельмен сипатталады.

Максвеллдiң механикалық модель Гук пен Ньютон элементтерiн тiзбектеп қосқанда алынады. Екi элементке де бiрдей кернеу әсер етедi.

Кельвин мен Максвеллдiң жалпыланған моделерiне тұтқырлық пен серпiмдiлiк қасиеттерi тән. Сондықтан олардың кернеу әсерiнен деформациялануы Кельвина-Фойгттың және Максвеллдiң денелерiнiң құраушы элементтерiнiң қосындысына тең.

Шведов-Бингамның тұтқыр-пластикалық денесiнiң екi элементтi механикалық моделi Ньютон және Сен-Венанның параллель қосылған элементтерiнен құралады. Егер болса, онда дене деформацияланбайтын абсолюттi қатты дене күйiнде болады.

Бингамның механикалық моделi Гук, Ньютон және Сен-Венанның элементтерiнен тұрады. Шведов моделiнi кезндегi деформациялануы Гук элементiне байланысты болады.
3. Нақты дененің алдын-ала жасалған эксперименттер нәтижесінде «идеалды» реологиялық денелердің қай түріне жататындығын анықтап білу зерттеуге арналған аспапты таңдауға және оқып меңгеруге қажетті қасиеттерін анықтауға мүмкіндік береді.

Сонымен математикалық моделдеу негізінде жіктеудің феноменологиялық (объективті шындықты есепке алмай) тәсілі жайында қарастырамыз.

Р. И. Щищенко ұсынған қатынасының шамасы бойынша заттың өз пішінін сақтап қалу қабілеттілік өлшемін көрсететін нақты денелердің қарапайым классификациясымен танысайық.

, м

0, 005-тен төмен

0, 005-0, 02

0, 02-0, 15

0, 15-тен жоғары

, м: Зат

0, 005-тен төмен: Құрылымдық сұйықтар

0, 005-0, 02: Сұйық пасталар

0, 02-0, 15: Қоймалжың пасталар

0, 15-тен жоғары: Қатты денелер

Б. А. Николаев механикалық қасиеттерінің шамасы бойынша (серпімділік модулі, тұтқырлық) денелердің жалпыланған жіктелуін ұсынды. Бірінші топқа ол қатты және қатты тәріздес денелерді (қатты май, еттің тұтас бөліктері, печенье және тағы басқалар) ; екінші топқа қатты-сұйық (ет фаршы, ірімшік және тағы басқа) ; үшінші топқа сұйықтарды және сұйық тәріздес заттарды (еріген май, сүт, сорпа, бал, су және т. б. ) жатқызды.

Нақты денелердің дәрежелік теңдеу көмегімен жіктелуін қарастырайық:

мұндағы В ₁ ^* - жылдамдық градиентінің бірлік мәніндегі тиімді тұтқырлыққа пропорционал коэффициент; n - логарифмдік шкалада ағу сызығының көлбеулік бұрышын сипаттайтын ағу индексі.

Кестеде 1. 1 өз қасиеттерін уақытқа сәйкес өзгертпейтін жүйелер көрсетілген. Кейбір жүйелер өз қасиеттерін уақытқа қатысты өзгертеді: мысалы, тиксотропты - ығысу кернеуі және тиімді тұтқырлығы ығысу кезінде азаяды; реопектті - жылдамдық градиенті тұрақты болған кезде жүйеге жанама кереулер әсер еткенде ығысу кернеуі мен тиімді тұтқырлық біртіндеп өседі.
Н. В. Михайлов және П. А. Ребиндердің реологиялық денелерін тиімді тұтқырлығына және релаксация периодына байланысты сұйық тәріздес және қатты тәріздес деп бөледі.

Сұйық тәріздес жүйелерге шектік ығысу кернеуі болмайтын ньютондық сұйықтар мен құрылымдық жүйелер, қатты тәріздес жүйелерге статикалық және динамикалық қасиетіне ие болатын серпімді-пластикалық, шартты пластикалық және басқа денелер жатады. Дисперсті жүйелердің құрылымдық механикалық қасиетінің негізгі сипаты ретінде тиімді тұтқырлықтың кернеуден және ығысу жылдамдығынан тәуелділігін қабылдайды. Себебі тиімді тұтқырлық қалыптасқан ағындағы құрылымының бұзылу және қалпына келу процестері арасындағы тепе-теңдікті сипаттайтын негізгі сипаттама болып табылады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.