Арнаулы салыстырмалық теориясы

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 54 бет
Таңдаулыға:

Қазақстан Республикасының білім және ғылым министрлігі

М. ӨТЕМІСОВ атындағы БАТЫС ҚАЗАҚСТАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

Кенжалиев Д. И.

Электродинамика және арнаулы салыстырмалық теориясы

«Физика», «Физика және информатика» және «Математика» мамандықтары бойынша оқитын студенттерге арналған оқу құралы

Орал - 2007

ӘОЖ 530. 12:531. 18(07)

КБЖ 22. 313я73

К 30

Автор :

Кенжәлиев Д. И. - физика-математика ғылымдарының кандидаты, доцент

Пікір жазғандар :

Тлеугалиев С. Х. - ф. -м. ғ. к., доцент, физика кафедрасы, М. Өтемісов атындағы БҚМУ

Нұрмағамбетов М. Ш. - доцент, физика кафедрасының меңгерушісі, Жангірхан атындағы БҚАТУ

Кенжәлиев Д. И.

К 30 Электродинамика және арнаулы салыстырмалық теориясы. Жоғарғы оқу орындарының студенттеріне арналған оқу құралы. - Орал: М. Өтемісов атындағы БҚМУ баспа орталығы, 2007. - 150 б.

Екінші түзетілген басылым

ISBN 9965-748-38-1

М. Өтемісов атындағы БҚМУ Оку-әдістемелік Кеңесі ұсынған

Ұсынылып отырған оқу құралында автор теориялық физиканың маңызды бөлімі классикалық электродинамика мен арнаулы салыстырмалық теория негіздеріне шолу жасаған. Бұл мәселелер мектептің физика курсының бағдарламасында алатын орны үлкен. Сол себепті болашақ физика пәнінің оқытушысының бұл саладан білімі терең болуы тиіс. Сонымен бірге болашақ ғалым, инженер және техникалық қызметкер үшін де электродинамикадан білімі саяз болмағаны қажет. Осы тұрғыдан теориялық физика пәнінің болашақ маман үшін маңызы жоғары. Бірақ қазір теориялық физиканың осы бір маңызды бөліміне арналған, және қазақ тілінде жазылған оқулықтар жоқ, ал оқу құралдары жоқтың қасы. Автордың бұл оқу құралы мол сұраныстың орнын толтырар деп үміттенеміз.

К КБЖ 22. 313я73

ISBN 9965-748-38-1

МАЗМҰНЫ

Кіріспе . . . 5

І Тарау. Арнаулы салыстырмалық теориясы . . . 11

§1. Салыстырмалық теорияның негізгі принциптері . . . 11

§2. Арнаулы салыстырмалық теориясының негізгі түсініктері. . 16

§3. Галилей түрлендірулері . . . 18

§4. Арнаулы салыстырмалық теориясы постулаттарының салдары . . . 21

§5. Бір санақ жүйесінен екіншісіне өту формулаларын (Лоренц түрлендірулерін) қорыту . . . 24

§6. Лоренц түрлендірулерінің салдары . . . 27

§7. Жылдамдықтарды түрлендірудің релятивистік формуласы . . . 29

§8. Оқиғалардың арасындағы интервал . . . 32

§9. Минковский әлемінде Лоренц түрлендірулерінің мәні . . . 35

§10. Салыстырмалылық теориясының 4 өлшемді

кинематикасы . . . 38

§11. Салыстырмалылық теориясының 4 өлшемді

динамикасы . . . 42

§12. АСТ-да 4 өлшемді векторлардың түрленуі . . . 46

§13. Өзара әсерлесудің релятивистік моделі. Өріс туралы түсінік . . . 49

§14. Жарық квантын-фотонды релятивистік бөлшек түрінде қарастыру . . . 51

§15. Допплер эффектісі . . . 53

II тарау. Электродинамиканың негізгі теңдеулері . . . 58

§16. Электродинамиканың негізгі ұғымдары . . . 58

§17. Вакуумдегі электр заряды . . . 64

§18. Электромагниттік өріс. Кернеулік, магнит өрісінің индукциясы 66

§19. Электродинамиканың эксперименттік негіздері. Электростатика заңдары . . . 69

§20. Вакуумдегі электромагниттік өріс үшін Максвелл теңдеулері . . . 74

§21. Максвелл теңдеулерінің интегралдық түрі . . . 76

§22. Электромагниттік өрістің потенциалдары . . . 78

§23. Потенциалдар арқылы жазылған электромагниттік өріс теңдеулері . . . 80

§24. Потенциалдар үшін жазылған өріс теңдеулерінің шешімдері . . . 81

§25. Электродинамиканың релятивистік тұжырымдамасы . . . 82

§26. Электромагниттік өріс тензоры және Максвелл теңдеулерінің ковариантты формасы . . . 87

§27. Е және В векторларынан бір ИСЖ-дан екіншісіне өткендегі түрленуі. Өріс инварианттары . . . 90

§28. Зарядталған бөлшектің сыртқы электромагниттік өрістегі қозғалыс теңдеулерінің ковариантты түрі . . . 93

§29. Зарядтарды орын ауыстыруға өрістің істейтін жұмысы . . . 94

§30. Электромагниттік өрістің энергиясы. 95

§31. Электромагниттік өріс импульсы. Импульстың сақталу заңы. … 97

III Тарау. Электромагниттік өрістің жеке мысалдары . . . 99

§32. Вакуумдегі стационарлы электромагниттік өріс теңдеулері . . . ……… 99

§33. Зарядтар жүйесінен өте алыс нүктелердегі электростатикалық өріс…… . . . . . . …. . 103

§34. Электростатикалық зарядтар жүйесінің энергиясы…… . . . 106

§35. Сыртқы электр өрісінде тыныштықта тұратын зарядтар жүйесіне әсер күші . . . …… . . . 109

§36. Вакуумдегі магнитостатикалық өріс . . . 111

§37. Алыс нүктелердегі зарядтар жүйесінің вектор- потенциалы . . . 112

§38. Сыртқы магнит өрісінде қозғалатын зарядтар жүйесінің энергиясы, күш . . . … 115

§39. Электромагниттік толқындар. . 118

§40. Электромагниттік толқындарды шығару 125

§41. Қозғалыстағы зарядтар жүйесінен алыс нүктелерде электро-магниттік өріс потенциалдары . . . . . . ……… . . . 128

§42. Электрлік дипольдық сәуле шығару . . . …… 132

§43. Сәуле шығарушы жүйелер . . . 134

§44. Магниттік дипольдық сәуле шығару . . . 136

§45. Толқындық және квазистатикалық зоналар 137

§46. Электромагниттік өрісте зарядтың қозғалу мәселесі……. 138

Қосымша. Электродинамика өлшем бірліктері жүйелері. . 143

Қорытынды. . 147

Әдебиет. . 148

КІРІСПЕ

Қазіргі заман техника мен ғылымның екпінді дамуымен сипатталады. Даму негізінде - фундаменттік ғылымдардың жетістіктері. Солардың ішінде физиканың алатын орны ерекше. Бұл ғылым ғылми-техникалық прогресстің негізі болып табылады. Әсіресе, электромагниттік процесстерді зерттеу және қолдану кең өріс алған. Электромагниттік өрісті зерттейтін ғылым электродинамика - теориялық физиканың маңызды бөлімі болып табылады. Бұл саланың тарихи маңызы: ол физика ғылымының дамуына ерекше түрткі берген сала. Электродинамиканың теориялық принциптерінің қалыптасуы кезінде классикалық физиканың шектелгендігін көрсетіп, жаңа физиканың пайда болуына себепші болды. Классикалық физиканың теориялық негіздерінің кемшілікте-рі оптикалық құбылыстарды классикалық физика тұрғысы-нан түсіндіру әрекеттерінің сәтсіздігінен көріне бастады. Ғылымда пайда болған дағдарысты жеңу жолында физика-ның фундаменттік , яғни негізгі принциптерін қайта қарау қажет болды. Осының нәтижесінде физиканың жаңа салала-ры: салыстырмалық теория және кванттық механика пайда болды. Соның көмегімен көптеген құбылыстар мен зат қасиеттері түсіндірілді, техникада қолданыс тапты.

Сонымен, физика ғылымының негіздеріне сипаттама берейік. Бұл ғылым - тәжірибелік болса да, теориясыз дамуы мүмкін емес. Теория ғана оны түсінікті қылады, әрі практика-да қолданылатын жасайды. Физикалық теория өте ауқымды дүние болып табылады, оның ішінен фундаменттік бөлім бөлініп шығады. Бұл бөлім материя құрылысы және қозғалы-сы жайындағы білімнің негізін құрайды. Осы фундаменттік теория физиканың басқа бөлімдерін біріктіріп, бағыттап тұрады. Педагогтік тұрғыдан фундаменттік білімнің маңызы әрқашан жоғары болды. Ол оқушылардың ғылыми көзқара-сын қалыптастырады. Ол мектептік курсының құрамына кіріп, әлемнің біртұтас көрінісін туғызады. Өткен ғасырда материалдық әлемнің бірлігі жөніндегі көзқарас жаңа қырынан көрінді, бірнеше фундаменттік өзара әсерлер бөлініп алынды. Бұлар материалдық объектілердің қозғалысы мен күйінің өзгерісіне жауапты. Бұл гравитациялық, электр-магниттік, ядролық күшті және әлсіз әсерлер (1-сурет) . Осылардың ішінде жақсы зерттелгені: электрмагниттік әсер. Басқалардың қасиеттерінің зерттелу дәрежесі ондай емес. Электромагниттік өріс еркін және зарядтармен байланысқан күйінде болуы мүмкін. Тыныштықтағы зарядтардың маңын-дағы өрісті электростатикалық , ал стационарлы қозғалып тұрған зарядтар жүйесінің маңындағы өрісті стационарлы өріс деп бөледі.

Физикалық теорияның құрылымы қандай? Бұл мәселе бойынша Эйнштейн: физикалық теория- 1. Түсініктер 2. Негіз-гі принциптер. 3. Солардан шығатын салдар деп бөлінетінді-гін айтады. В. Гейзенберг теорияның маңызды қасиеті деп физикалық құбылыстардың белгілі бір бөлігін мейлінше толық сипаттайтын түсініктер жүйесінің тұйықтығын айтады. Ал қазіргі ғылми-техникалық деңгей тұрғысынан физикалық теория дегеніміз не? Біз бұл мәселені талдауда белгілі ғалым В. В. Мултановскийге [12] ерейік. Тарихи жағынан алсақ, қандай да физикалық теория өзінен бұрыңғы теорияның түсіндіре алмаған тәжірибелік фактілерден өсіп шығады. (Бұл бір сәтте пайда болмайды, біртіндеп өседі, оның алдында кейде күшті талас-тартыс пайда болуы мүмкін) . Зерттеушілер осы тәжірибелік фактілерден болашақ теорияның зерттейтін объектісін бөліп алады. Мысалы, электродинамика пайда болмастан бұрын электричествоның, магнетизмнің және оп-тиканың дербес теориялары болған. Бірақ зерттеулер жалғаса берген сайын бұрыңғы теориялардың аумағына сыймайтын фактілер көбейді. Бұл, негізінен, жоғарыда аталған үш сала-дағы құбылыстардың бір-бірімен байланысын көрсететін және т. б. фактілер болып табылады. Содан барып пайда болған қайшылықтарды түсіндіру мақсатымен теорияның не-гіздері қайта қаралып, нәтижесінде зерттелінетін идеалдан-ған объект : электромагниттік өріс екендігі анықталады.

Кез келген физикалық теорияда негіз , ядро , қорытын-дылар болады (2-сурет) . Әрбір бөлігі- танымдық қызметтің сатыларымен сәйкес келеді, теория элементтерінің бір тобын қамтиды, ал ең үстінде теорияның жалпы интерпретациясы қойылады. Теорияның тұйықтығы дегені танып-білудің цикл-ді сипатын ғана білдірмейді өз шеңберіндегі барлық құбы-лыстарды мейлінше толық сипатталатындығын білдіреді. Жеке -жеке қарастырайық:

Негіз . Өзі пайда болмастан бұрын болған теориялардың түсіндіре алмайтын эксперименттік фактілердің бір тобы сұрыпталып, ой елегінен өткізіледі. Эксперименттік факті-лердің жиынтығы теорияның эмпирикалық базисін құрай-ды. Бұлар сол кездегі белгілі ережелермен салыстырылып, болашақта осыдан идеалданған объект бөлініп шығарыла-ды. Бұл азғантай ортақ қасиеттермен сипатталатын ең жай абстрактілі модель. Ол зерттелетін құбылыстар аумағының мағынасын, ерекшеліктерін моделді түрде көрсетеді. Бұдан кейін идеалданған объектінің қасиеттерін танып-білу керек. Бұл үшін фундаменттік шамалар жүйесі (әрқайсысы оның белгілі бір қасиетін сипаттайды) . Белгілі бір әдіспен жасала-тын физикалық өлшеулер, оларға қолданылатын математика-лық амалдар жүйесі теория негізінің құрамдас бөлігі болып кіреді. Эмпирикалық базис, идеалданған объект, негізгі физи-калық шамалар (Е, В), оларды өлшеу әдісі, оларға істелетін математикалық амалдар жиынтығы- физикалық теорияның қалыптасуының алғашқы сатысын құрайды. Оны негіз деп атайды. Негізден басқа теорияны құрайтындар: ядро және қорытындылар.

Ядро дегеніміз математикалық теңдеулер арқылы өр-нектелген жалпы заңдар жүйесі. Олар физикалық шамалар-дың арасындағы байланыстарды анықтайды, осы шамалар-дың уақыт өткен сайынғы және кеңістіктегі өзгерісін береді.

Бұл әдетте дифференциалдық теңдеулер жүйесі, немесе негізгі принциптер жүйесі. Сонымен, ядро дегеніміз теория-лық жалпылаудағы идеалданған объектіге қатысты байла-ныстар мен қатынастардың ең жалпы математикалық моделі. Ядродан негізгі постулаттар мен принциптерді бөліп алуға болады. Бұл - теңдеулердің сөзбен өрнектелген тұжырымда-малары немесе соларға келтіретін ережелер. Мысалы, салыс-тырмалық теория екі постулатқа негізделіп құрылған. Ядрода сақталу заңдары (энергия, импульс, импульс момен-ті, жұптық, электр және басқа зарядтардың сақталу заңдары) . Сақталу заңдарының негізгі тобының ортақ негізі - кеңістік-тік-уақыттық симметриялар. Сақталу заңдары теория теңдеу-лерінен салдар болып шығуы тиіс. Ядроға негізгі теңдеулер-дің түрлендірулердің қандай да тобына инварианттылығы да, онымен байланысты заңдылықтар мен константалар да кіреді. Теория теңдеулерге кіретін константаларды өлшеу арқылы нақты қорытындыларды жасай алады. Әртүрлі теориялардың негізгі түсініктері мен теңдеулерінің арасындағы көптеген байланыстар да ядроға кіреді.

Қорытындылар . Түптеп келгенде, теорияның міндеті ядродан нақты қорытындылар шығару. Теорияны қорыту процесінде әртүрлі физикалық шамалардың арасында функциялық тәуелділіктер пайда болады. Оларды сандық қорытындылар деп атайды. Қазіргі заманғы теорияларда олардың саны көбейе түседі. Олардың бірқатары қасиеттердің жеке аумағы үшін ғана қолданылады. Теория өз облысында кез келген қорытындыны шығара алуы тиіс. Бірақ кейбір фактілерді түсіндіре алмауы мүмкін. Бұл болашақ теорияның міндетіне кіреді. Теорияның маңызды қызметі - жаңа құбылыстарды болжау. Қорытындыларға теорияның интерпретациясы да кіреді. Интерпретация деп берілген түсініктер шеңберінде қорытындылардың физикалық түсіндірілуін айтамыз.

Кең мағынада электродинамикаға бірнеше теория кіреді. Бұл Максвеллдің феноменологиялық теориясы , Лоренцтің электрондық теориясы ( классикалық электрондық теория деп те атайды) және арнаулы салыстырмалық теория.

Максвелл теориясы феноменологиялық , яғни макроско-пиялық теория атануы оның ерекше сипатын білдіреді. Яғни бұл теория заттың нақты құрылымы болатындығын ескер-мейді. Зат кеңістіктің өріс алып жатқан қандай да бір бөлігін үздіксіз толтырады, ал осы бөліктегі өрістің қасиеттері диэлектрлік және магниттік өтімділіктер тәрізді коэффициен-тер арқылы ғана ескеріледі. Зарядтардың дискреттігі де, яғни электрондар тәрізді ұсақ бөлшектерден құралатындығы еске-рілмейді. Теорияның феноменологиялық болғаны оның шек-телгендігінің белгісі. Осы шектелгендігін жою үшін Лоренц заттың құрылымын ескеретіндей теорияға өзгерістер енгізген болатын. Лоренцтің электрондық теориясы структуралық теория болып табылады және оны микроскопиялық элект-родинамика деп те атайды. Бұл теория классикалық электрондық теория деп те аталады, өйткені оған кванттық физика көзқарастары енгізілген жоқ.

Сонымен бірге электродинамика релятивистік теория болып табылады, яғни оның кеңістік пен уақытқа, қозғалысқа өзара әсерге деген көзқарастары арнаулы салыстырмалық теорияның көзқарастарына жақын.

Электродинамиканың қорытындылары есептеуіш техниканың, радиолокацияның негізін құраған электроника, радиотехника салаларының фундаменті болып табылады.

Автордың көздеген мақсаты: электродинамика мен арнаулы салыстырмалық теория пәндерінің негізгі мәселеле-ріне сипаттама беру. Оқу құралы «Физика» мамандығы бой-ынша бағдарламаға сәйкес құрылған. Сондықтан оған Лорен-цтің электрондық теориясы кіргізілмеген. Сол сияқты ортада-ғы электромагниттік өрісті қарастыру да автордың мақсатына кірмейді. Құрал 3 бөлімнен тұрады: бірінші бөлімде арнаулы салыстырмалық теорияның негізгі мәселелері баяндалады. Оның негізгі постулаттары тұжырымдалып, одан салдар шы-ғарылады. Лоренц түрлендірулері негізделіп, интервал ұғы-мы енгізіледі. Салыстырмалық теорияның ең ыңғайлы мате-матикалық аппараты - тензорлық анализ негіздері беріледі. Екінші бөлімде электрдинамиканың негізгі теңдеулері келті-ріліп, сақталу заңдары негізделеді. Үшінші бөлімде электр-магниттік өрістің жеке жағдайлары: тұрақты электрмагниттік өріс пен электрмагниттік толқындардың теңдеулері және олардың заттан шығарылу мәселелері баяндалған.

Жалпы алғанда, электрдинамика мен арнаулы салыс-тырмалық теорияға арналған осы оқу құралы оқырманның аталған мәселелерді меңгеруіне көмегі тиер деген үміттеміз.

І Тарау. АРНАУЛЫ САЛЫСТЫРМАЛЫҚ ТЕОРИЯСЫ

§1. Салыстырмалық теорияның негізгі принциптері

Ньютонның заңдарына негізделген классикалық меха-ника тек макроскопиялық денелерге, яғни өте көп бөлшектер-ден (иондардан, атомдардан, молекулалардан және т. б. ) құралатын денелерге қолдануға болатыны белгілі. Сонымен қатар, бұл макроскопиялық денелер жарықтың вакуумдағы жылдамдығына қарағанда өте төменжылдамдықпен қозғалуы қажет. Вакуумдағы жарық шамамен 3 км/с жылдамдық-пен қозғалғандықтан, практика жүзінде классикалық механи-каны қарапайым денелердің барлығына қолдануға болады. Элементар бөлшектер, жеке атомдар, иондар, молекулалар және т. с. с. өздерінің қозғалысында өте үлкен жылдамдық алулары мүмкін. Ондай бөлшектерді бақылау нәтижелері классикалық механиканың заңдылықтарынан ауытқу болатынын көрсетеді.

Өте үлкен жылдамдықпен қозғалатын денелердің меха-никасы салыстырмалық теориясы деп, немесе релятивис-тік (реляцион- салыстырмалық, лат. ) теория деп те аталады. Жарықтың вакуумдағы жылдамдығымен шамалас жылдам-дықтар релятивистік жылдамдықтар , релятивистік жыл-дамдықтармен қозғалатын денелердің механикасы реляти-вистік механика , релятивистік механикада зерттелетін құбылыстар релятивистік құбылыстар деп аталады.

Релятивистік теорияның негізін қалаған - Альберт Эйштейн (1905ж. ) . Салыстырмалық теориясының екі түрі бар- арнаулы салыстырмалық теориясы және жалпы салыстырмалық теориясы . Арнаулы салыстырмалық тео-риясында бірқалыпты, бірақ өте үлкен жылдамдықпен қозға-латын денелер қарастырылса, жалпы салыстырмалық теория-сында өте шапшаң, бірқалыпты емес, үдемелі қозғалыстағы денелер қарастырылады. Біздер тек қана арнаулы салыстырмалық теорияны қарастырамыз.

Арнаулы салыстырмалық теориясы(АСТ) ХХ ғасырдың басында пайда болған физиканың жаңа бөлімі. Ол үлкен қашықтықтарда және өте жоғары жылдамдықтарда физика құбылыстарында, заңдылықтарында байқалатын өзгерістерді түсіндіруді мақсат етеді. Бұндай ерекше жағдайларда дене-лердің қозғалысының физикалық қасиеттерін түсіну үшін кеңістік пен уақытқа деген бұрыңғы көзқарастарды талдап, олардың негізгі қасиеттерін қайта қарауға тура келді. Сонымен, кеңістік пен уақыттың негізгі қасиеттерін зерттей-тін теориялық физиканың бөлімі- салыстырмалық теория.

Кеңістік пен уақыттың қасиеттері әртүрлі физикалық құбылыстардан байқалады. Адам санасында қалыптасып қалған қасиеттер механикалық қозғалыстардан, яғни күнделікті өмірден көрінеді. Бірақ нақты қасиеттер басқа құбылыстардан анық байқалады. Сондай құбылыстардың бір класы- жарық толқындарының таралу заңдылықтарынан білінді. Екінші класы- ядролық құбылыстардан (микродүние) және космостық денелердің қозғалыстарынан (макродүние) байқалды. Сондай құбылыстардың үшінші класы- үлкен массалы денелердің маңындағы кеңістік пен уақыттың қасиеттерінің өзгерісімен байланысты.

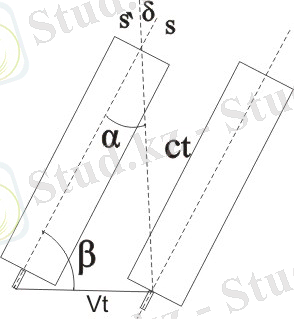
Арнаулы салыстырмалық теориясының негізінде Эйнштейннің салыстырмалылық принципі жатыр. Механикада осыған ұқсас Галилейдің салыстырмалылық принципі қабылданған: Барлық инерциалды салыстырмалы санақ жүйелерінде механикалық құбылыстар бірдей өтеді. Немесе: ешқандай механикалық құбылыстарды пайдаланып, санау жүйесінің тыныштықта тұрғанын немесе бірқалыпты түзу сызықты қозғалыста екенін анықтауға болмайды. Бірақ электромагниттік өріс заңдары Галилейдің салыстырмалы принципіне қайшы келеді (сол себепті ХХ ғасырдың басында салыстырмалы принциптің мағынасын кеңейту мәселесі пайда болды) . Бұл қайшылықты дәлелдейтін экспериментальдық фактілер: Майкельсон - Морли тәжірибесі, Физо тәжірибесі, астрономиялық аберрация эффектісі . Бұл тәжірибелерден шығатын негізгі қорытынды: Барлық санақ жүйелерде өлшегенде C= 3*10 ⁸ км/с-қа тең. Майкельсон - Морли тәжірибесінде (3-сурет) жарық сәулесі S жарық көзінен шығып, П- жартылай мөлдір әйнекте екіге бөлінеді. екі сәуле- ұзындықтары бірдей ПА=ПВ= l қашықтықтарды өзара перпендикуляр бағытта жүріп өтеді және А мен В айналардан шағылады. 1-сәуле П пластинадан өтіп, ал 2-сәуле одан шағылғаннан кейін Т тұрбаға түсіп, егер екеуінің жылдамдықтары әртүрлі болып, фаза айырмашылықтары пайда болса, интерференция құбылысын туғызуы тиіс. Бұл тәжірибенің идеясын 1879 жылы Максвелл айтып, 1881 жылы Майкельсон орындады (идеясы мен теориясын Беллюстин[5] кітабынан оқуы-ңызға болады. ) . Тәжірибенің мақсаты-Жердің эфирге қатыс-ты V жылдамдығын өлшеу. Бірақ екі сәуледе фаза айыры-мы пайда болмады, демек Жер эфирге қатысты қозғалмайтын немесе эфир Жермен бірге іле-сіп қозғалатын болып шықты. Бірақ соңғы қорытындыны Физо тәжірибесі растамады. (Физо тәжірибесінің сипаттамасы §7-де)

Жұлдыздық аберрация құбылысы дегеніміз бақы-лаушының қозғалысы сал-дарынан жұлдыз кескінінің-(S) шын (яғни нақты) (S') қалпынан ауытқу құбылы-сын айтады. Бұның себебі Жердің орбиталды қозғалы-сы, ал ауытқу осы қозғалыс-тың V жылдамдығына ғана тәуелді. Эфир Жермен ілесе қозғалатын болса, бұндай құбылыс байқалмауы тиіс еді. [8] (V≈30 км/с) (4-сурет)

Осы 3 тәжірибенің нәтижесі физикада дағдарыс туғыз-ды. Дағдарыстан шығу үшін Галилейдің салыстырмалық принципінен бастарту керек немесе электродинамиканы басқаша құру керек, екеуі бір-біріне үйлеспейтін сияқты болды. Дағдарысты жеңудің жолын Эйнштейн тапты. Ол салыстырмалық принципін (постулатын) және электродина-мика принциптерін үйлестіру мүмкін деп тапты.

Физика дамуы арқасында физикалық қозғалыстың мағынасы кеңейіп, қозғалыстың басқа түрлерін де қамтыған, соның ішінде электромагниттік өрістің қозғалысы да бар. Альберт Эйнштейн бұл постулатты кеңейтіп, механикалық қана емес, электрлік, магниттік, оптикалық, ядролық, атом-дық, молекулалақ, жалпы физикалық құбылыстарды пайда-ланып, санау жүйесінің тыныштықта тұрғанын немесе бірқа-лыпты түзу сызықты қозғалыста екенін айырып білуге бол-майды дейді. Сонымен, Эйнштейннің салыстырмалылық принципі: Барлық инерциалды санақ жүйелерінде физикалық құбылыстардың мағынасы өзгермейді, яғни бірқалыпты қозғалыс физикалық құбылыстардың өтуіне әсерін тигізбейді , - дейді. Басқаша айтқанда, ешқандай физикалық құбылыстарды пайдаланып санау жүйесінің тыныштықта тұрғанын немесе бірқалыпты түзу сызық-ты қозғалыста екенін ажыратуға болмайды.

Осы тұжырым және жарық жылдамдығының тұрақ-тылығы жөніндегі постулат арнаулы салыстырмалық тео-риясының негізгі постулаттары болып табылады.

Арнаулы салыстырмалық теориясының негізгі мәселесі: Инерциалды санақ жүйесінің (ИСЖ) бәрінде де бірдей бөлі-нетін физика заңдарын анықтау, яғни барлық инерциалды санақ жүйесі табиғат құбылыстарын сипаттау бірдей болуы үшін қажетті шарттарды анықтау болып табыла-ды. Бірақ бұндай зерттеулерді жүргізу үшін кеңістік пен уақыттың негізгі қасиеттерін қайта қарап, адам санасында қа-лыптасып қалған кейбір қате көзқарастардан бас тарту керек болды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.