Векторлық диаграмма әдісімен синусоидалы ток тізбектерін есептеу

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Семей қаласының Шәкәрім атындағы комерциялық емес акционерлік қоғам «Ақпараттық - коммуникациялық технологиялар» факультеті

«Геодезия және құрылыс» кафедрасы»

Реферат

Тақырыбы: «Синусоидалы ток тізбегін есептеу әдістері. Актив және реактивтік қуаттар теңгерімдері. »

Орындағын: Саулебеков Д. Ж

Тексерген: Турусбекова Б. Ш.

Семей қаласы

2020-2021 оқу жылы

Жоспар:

Кіріспе
Негізгі бөлім
Қорытыңды бөлім.
Қолданылған әдебиеттер.

Кіріспе

Синусоидальды токтары мен кернеулері бар электр тізбектерін есептеу комплекстік сандарды қолдану арқылы едәуір жеңілдетілген. Сондықтан синусоидалы тербеліс векторларын комплекс түрінде жазықтықтың осьтерінде комплекстер түрінде бейнелеу принциптерін мұқият оқып, түсініп, кері өтуді - ток, кернеу және ЭҚК комплекстерінен олардың лездік мәндеріне дейін игеру қажет.

Белсенді кедергі, индуктивтілік және сыйымдылық түріндегі электр тізбектерінің идеалданған элементтері үшін токтар мен кернеулер арасындағы байланысты үйрену маңызды. Есіңізде болсын, белсенді қарсылықтағы ток фазадағы оның кернеуімен, оның индуктивтіліктегі күші артта қалады, ал сыйымдылықта ол периодтың төрттен біріне сәйкес келеді.

Электр тізбектерінің идеалдандырылған элементтерінің қасиеттерін зерттеу кезінде индуктивтілік пен сыйымдылықтың реактивтіліктері жиіліктің функциялары болып табылатындығын және осы кедергілердің көмегімен сәйкесінше өзіндік индукция мен орын ауыстыру токтарының тізбек режиміне ЭҚК әсерін ескеру қажет. Әр түрлі элементтері бар тізбектер үшін кедергі және өткізгіштік кешендерінің өрнектерін есте сақтау қажет. Сонымен қатар, жетекші және артта қалған токтары бар пассивті екі терминалды желі үшін токтар мен кернеулердің белсенді және реактивті компоненттері арасындағы байланысты аналитикалық және графикалық түрде (векторлық диаграмманы қолдану арқылы) құру тиімді.

Тұрақты токтар мен кернеулердегі сызықтық электр тізбектерін есептеудің барлық әдістері синусоидальды токтар мен кернеулерде өзара индукциясыз электр тізбектеріне толығымен таратылады. Бұл жағдайда токтар, ЭҚК және кедергілер электр күйінің теңдеулеріне кешендер түрінде енуі керек. Электр тізбектерін есептеу үшін қолданылатын негізгі заңдар - Кирхгоф заңдары.

Кез-келген электр тізбегін есептеудің пайдалы иллюстрациясы - бұл электр тізбегінің кез-келген нүктелері арасындағы кернеуді қосымша есептеусіз графикалық түрде табуға мүмкіндік беретін оның топографиялық диаграммасы.

Өзара индуктивтілігі бар тізбектерде кернеу компоненттерінің жаңа түрі пайда болады, бұл өзара индукцияның ЭҚК-іне байланысты. Осыған байланысты өзара индукциясы бар тізбектерді есептеу өзара индукциясы жоқ ұқсас конфигурация тізбектерін есептеуге қарағанда біршама күрделі. Мысалдарды қолдана отырып, осындай тізбектерді есептеу әдістемесін үйрену оңай. Өзара индукциясы бар тізбектің маңызды практикалық мысалы - темір өзегі жоқ трансформатор.

Негізгі бөлім.

Векторлық диаграмма әдісімен синусоидалы ток тізбектерін есептеу

Синусоидалы токтың электр тізбегінің әртүрлі секцияларындағы ток пен кернеу, әдетте, фазада сәйкес келмейді. Әр түрлі векторлардың фазалық орналасуының визуалды көрінісі токтар мен кернеулердің векторлық диаграммасында келтірілген. Бұл есептеулерді сапалы басқара алу үшін векторлық диаграммаларды құра отырып, синусоидалы токтың электр тізбектерінің аналитикалық есептеулерін сүйемелдеу ұсынылады.

Сапалық бақылау аналитикалық есептеу арқылы алынған әр түрлі векторлардың күрделі жазықтықтағы бағыттарын физикалық ойларға негізделген осы векторлардың бағыттарымен салыстырудан тұрады. Мысалы, векторлық диаграммада UL кернеуі токтан 90 ° жоғары болуы керек, ал dc кернеуі токтан 90 ° артта болуы керек.

Егер аналитикалық есептеу осындай айқын позициялармен сәйкес келмейтін нәтиже берсе, демек, оған қате жіберілді. Сонымен қатар, векторлық диаграмма көбінесе есептеу құралы ретінде қолданылады, мысалы, пропорционалды шамалар әдісінде.

Мысал.

Тізбекте (3. 13-сурет. а ) e - 141sincot; B = 3 Ом; R2 = 2 Ом; L = 0, 00955 Гн Бұрыштық жиілік ω = 314 рад / с. Тізбек элементтеріндегі ток пен кернеуді анықтаңыз.

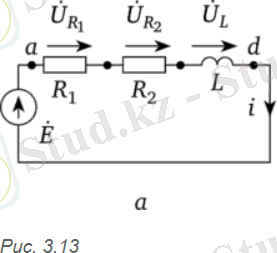
Шешім. Лездік мәндердің теңдеуін жазайық:

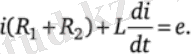
Одан комплекстердегі теңдеуге өтейік:

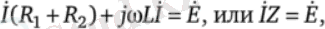
Мұндағы Z = Rl+R2 +; ooL = 3 + 2 +; 314 • 0, 00955 = 5 + 3j = 5, 82е>31°.

ЭҚК тиімді мәні кешені E = 141/л/ 2 = 100В.

Ток i-E/Z = 100/ (5, 8е-'31°) = 17, 2е^'31° А.

Кернеуі URl-Uab = /Я1 =51, 6е_-'31° В; R2 UR2-Ubc-iR2 = = 34, 4е->31° В, L UL = Ucd = ; wL7 = 3; 17, 2е->31° = 51, бе^ В.

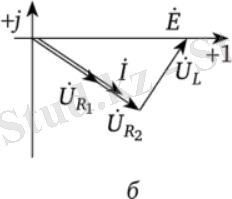
Векторлық диаграмма күріш. 3. 13, б. Е векторы +1 осі бойымен бағытталған. Ағымдағы вектор / одан 31 ° артта қалады.

Синусоидалы ток тізбектерін есептеудің символикалық әдісінің негіздері

Айнымалы синусоидалы ток тізбектерін есептеу тек векторлық диаграммаларды тұрғызумен ғана емес, сонымен қатар аналитикалық жолмен - синусоидалы ЭҚК, кернеулер мен токтарды символикалық түрде бейнелейтін кешендермен жүргізілуі мүмкін. Векторлық диаграммалардың артықшылығы - олардың айқындылығы, кемшілігі - графикалық конструкциялардың дәлдігінің төмендігі. Символдық әдісті қолдану схемалық есептеулерді жоғары дәлдікпен жүргізуге мүмкіндік береді.

Синусоидалы ток тізбектерін есептеудің символдық әдісі Кирхгоф заңдары мен Ом заңына күрделі түрде негізделген.

Кирхгоф заңдарын күрделі түрде өрнектейтін теңдеулер тұрақты ток тізбектерінің сәйкес теңдеулерімен бірдей формада болады. Тек токтар, ЭҚК, кернеулер мен кедергілер теңдеулерге күрделі шамалар түрінде енгізілген.

Кирхгофтың бірінші заңы (комплекстік) :

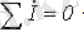
Кирхгофтың екінші заңы (комплекстік) :

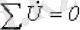
немесе ЭҚК көздері бар эквивалентті тізбектерге қатысты:

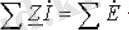
Тиісінше, Кирхгоф заңдарының матрицалық жазбасы комплекстік түрде:

§ Кирхгофтың бірінші заңы:

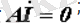
Кирхгофтың екінші заңы:

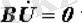
Синусоидалы ток тізбегін есептеудің комплекстік тәсілі.

Комплекстік тәсіл лездік мәндер үшін құрылатын дифференциалдық теңдеуден комплекстік мәндер үшін құрылатын алгебралық теңдеуге өткізуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде синусоидалық шамаларды комплекстік сандар ретінде көрсетеді:

А , мұндағы 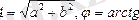b/a.

Егер 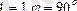, онда 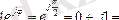. Егер 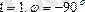, онда

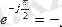
Кез-келген векторды -ға көбейткенде, ол вектордың модулін өзгертпей 90 ^о -қа бұрады., ал - -ға көбейткенде векторды - 90 ^о -қа бұрады ( 28-сурет) . Комплекстік тәсілді пайдалану арқылы синусоидалы шамалардың лездік мәндерін анықтайтын дифференциалдық теңдеулерден комплекстік мәндер арқылы өрнектелген алгебралық теңдеулерге көшуге болады. Бұл есептеу жұмысын жеңілдетуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде токтың лездік мәнін ( i ) оның комплекстік амплитудалық мәніне ( I _m ) айырбастаймыз, ал лездік активті кернеуді u _a =ir комплекстік активті кернеумен. I _m r, лездік индуктивті кернеуді u _L =L di/dt комплекстік индуктивті кернеумен I _m jωL, ал лездік сыйымдылық кернеуді u _C =(1/C ) ∫idt комплекстік сыйымдылық кернеумен I _m (-j/ωC ), лездік э. қ. к. -ті e комплекстік кернеумен E _m айырбастаймыз.

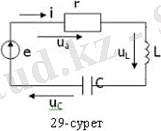
29-суретте көрсетілген тізбекке Кирхгофтың екінші заңы бойынша лездік мәндер үшін теңдеу құрайық: u _a + u _L + u _C = e, немесе

I _m r

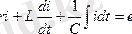
Теңдеуді комплекстік түрде жазайық: I _m r + I _m jωL - I _m (j/ωC ) = E _m , I _m [ r + j( ωL -- 1 /ωC ) ] = E _m ,

бұдан I _m = E _m / [ r +j ( ωL -- 1 /ωC ) ] = E _m / Z .

Бұл теңдеудің оң жағын да, сол жағын да √2 бөлсек, онда комплекстік әрекеттік мәндер үшін Ом заңын аламыз: I = E / Z . Мұндағы Z - тізбектің комплекстік кедергісі: Z =[ r +j( ωL -- 1 /ωC ) ] = r+jx = ze ^{j φ} . Комплекстік кедергінің нақты бөлігі активті кедергіге r , ал жорамал бөлігі реактивті кедергіге x = ( ωL -- 1 /ωC) тең. Комплекстік кедергінің модулі .

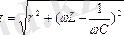Комплекстік өткізгіштік деп комплекстік кедергіге кері шаманы айтады:

, ,

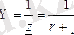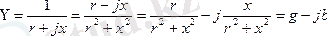
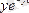мұндағы ,

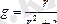- активті өткізгіштік, 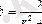- реактивті өткізгіштік, - толық өткізгіштік.

Ом заңын комплекстік өткізгіштік арқылы жазайық: I = U Y, I = U g - U b= I _a + I _p .

Сонымен электр тізбегінің толық өткізгіштігі нақты бөлігі активті өткізгіштікке, ал жорамал бөлігі реактивті өткізгіштікке тең комплекс сан ретінде жазылады.

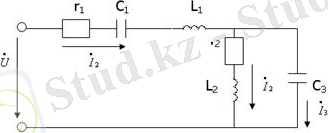30-сурет

30-суретте көрсетілген тізбектің тармақтарының комплекстік кедергілерін жазайық. Ол үшін алдымен активті және реактивті кедергілердің комплекстік түрде жазылуын көрсетейік: 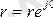= r , X _L , .

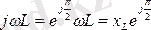X _C

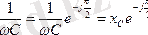
Тізбектің тармақтарының комплекстік кедергілері:

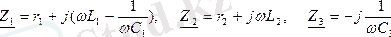
Тізбектің толық комплекстік кедергісі:

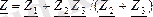
Комплекстік қуат деп кернеудің комплекстік әрекеттік мәнін түйіндес токтың комплекстік әрекеттік мәніне көбейткенге тең: 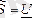Ỉ. Берілген комплекстік осы токтың модулімен бірдей, ал фазасы қарама-қарсы болып келетін токтыайтады . Айталық, 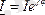- берілген ток болса, онда түйіндес ток Ỉ .

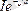Егер 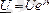болған жағдайда 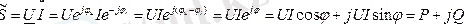, мұндағы

P = UIcosφ - активті қуат; 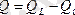= UIsinφ - реактивті қуат. Бұдан комплекстік қуаттың нақты бөлігі активті қуатқа тең, ал жорамал бөлігі реактивті қуатқа тең.

Комплекстік қуаттың көрсеткіш түрде жазылуы: =se ^jφ , мұндағы , .

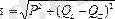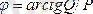Синусоидалы ток тізбегіндегі қуаттар тепе-теңдігі мынаны білдіреді: біріншіден, тізбектегі барлық қоректендіргіштердің активті қуаттарының алгебралық қосындысы сол тізбектегі резистивті элементтердің активті қуаттарының арифметикалық қуаттарының қосындысына тең:

∑U _қор I _қор cos(φ _u - φ _i ) = ∑rI _r ² немесе ∑P _қор = ∑P _r ,

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.