Пеано аксиомалары және натурал сандар теориясының негізгі салдарлары


Қазақстан Республикасы Білім және Ғылым Министірлігі
М. Өтемісов атындағы Батыс Қазақстан университеті
Сандар жүйелері
Тақырыбы: Пеано аксиомалары және оның кейбір салдарлары.
Дайындаған: Бозаев Тұрар
Тексерген: Лукпанова Ляззат
2020 жыл
Мазмұны
Кіріспе 3
- Аксиоматикалық теорияның негізгі түсініктері. 4
- Натурал сандар қатарының әдеттегі моделі.
Математикалық индукция әдісі 7
- Пеано аксиомалары және оның кейбір салдарлары. 8
Қорытынды. 9
Кіріспе
Аксиоматикалық әдіс - оның әртүрлі салаларында ғылыми білімді ұйымдастырудың және көбейтудің іргелі әдісі-ғылымның дамуының екі мың жылдан астам тарихында қалыптасты. Аксиоматикалық әдіс математика ғылымында ерекше рөл атқарады. Бұл математикалық ғылым кемелдікке жетеді кезде ғана оған мүмкін емес пайдалануға аксиоматическим әдісімен, т. е., қашан ғылым қабылдайды сипаты аксиоматической теориясы. Сонымен қатар, ХХ ғасырдағы ғылымның дамуы математика ғылым жүйесінде ерекше болып табылатындығын көрсетті, өйткені ол аксиомалық әдісті өте кең қолданатын жалғыз әдіс және бұл әдіс математиканың әлемді тану процесінде және оған трансформациялық әсер ету процесінде таңқаларлық тиімділігін анықтайды.
Математикада белгілі бір аксиомалық теориялардың қалыптасуының екі жолын көрсетуге болады.
Бірінші жол-бұл немесе басқа математикалық теория дамудың жеткілікті жоғары деңгейіне жетіп, аксиоматикалық теорияның сипатын алады. Келесі математикалық теориялар аксиоматизацияланды: арифметика (Дж. Пиано), геометрия (аксиомалардың әртүрлі жүйелеріне негізделген, атап айтқанда Д. Гильберт, г. Вейл, М. Пиери және т. б. ), Ықтималдық теориясы (а. н. Колмогоровтың аксиоматикасы) және басқалар.
Аксиоматикалық теориялардың пайда болуының екінші жолы-мүлдем басқа көрінетін математикалық теориялардың негізгі белгілері арасында терең ішкі ұқсастық анықталды. Бұл жағдай жалпы белгілерді бөліп көрсетуді және оларды басшылыққа ала отырып, аксиомалық теорияны құруды ұсынды. Бұл жолда барлық аксиоматикалық теориялар пайда болды, ең алдымен топтар, сақиналар, өрістер және басқа Алгебралық жүйелер, жалпы немесе әмбебап алгебра және т. б. Мұнда кейбір математикалық ғылымдардың әдістерін басқаларына өзара байланыстырудың тамаша мүмкіндігі, сонымен қатар аксиомалық теорияның бастапқы түсініктері мен аксиомаларын еркін түсіндіру мүмкіндігі бар, бұл осындай теорияларды қолданудың кең перспективаларын ашады және математиканың жалпы ғылым ретінде тиімді күшінің қуатты көздерінің бірі болып табылады.
Аксиоматикалық теорияның негізгі түсініктері.
Аксиоматикалық әдістің мәні туралы қазіргі түсініктің қалыптасуы ғылымның дамуының екі мың жылдан астам тарихында болды.
Геометриялық фигуралар мен денелер туралы ғылымның шынайы бастауы, әрине, мыңжылдықтардың тереңдігінде жоғалады. Алғашқы геометриялық көріністердің бастапқы дизайны әдетте Вавилон мен Египеттің ежелгі мәдениеттерімен байланысты (б. з. д. 3-2 мыңжылдық) . Б. з. д. VII ғасырдан бастап грек ғалымдарының еңбектерімен геометрияның даму пириоды басталады. Пифагор мектебі б. з. д. VI-V ғасырларда геометриялық зерттеулерді жалғастырды. Оның негізін қалаушы Пифагор (б. з. д. 560-470 немесе 580-500 ж. ж. ) жиырма жасында Мысырда, тағы он жасында Вавилонда даналықты оқыды. Пифагор мектебінде геометрия тар практикалық утилитарлық есептерден, жер учаскелерін өлшеу геометриясынан жалпылау, абстракциялар мен пайымдауларға алғашқы қадамдар жасағаны сөзсіз.
Ежелгі дәуірдің ұлы философы Платон (б. з. д. 428-348 ж. ж. ) академияның негізін қалаушы, бүкіл ғылыми білімді, атап айтқанда геометрияны дедуктивті түрде құру міндетін бірінші болып қойған сияқты. Геометрия туралы трактаттар мен оқулықтар Платоннан бұрын пайда болды - Хиос Гиппократы, Демокрит, Февдийдің басшылығы белгілі. бірақ тек Платон білімнің кез-келген саласының басында тұжырымдамалар мен ережелер болуын талап етті, олардан қалған барлық салалар олардың салдарына байланысты болуы керек. Бірақ Платонның бұл өнімі әлі күнге дейін бұлыңғыр және оның контурлары тек жартылай мистикалық базада салынған бүкіл ілімінен алынған.
Платонның керемет шәкірті ұлы Аристотель (384-322 ж. ж. ) Платонның мистикалық догмаларынан өтіп, кез-келген ғылыми іс-әрекеттің кез-келген білімін ғылыми негіздеудің ұтымды талаптарын анықтады. Ол өз уақытында қол жеткізген білімнің барлығын дерлік қамтыды, ғылыми әдіс пен көптеген ғылымдардың негізін қалаушы болды. Аристотельдің пікірінше, ғылым - бұл белгілі бір салаға қатысты сөйлемдер тізбегі. Бұл ұсыныстардың ішінде дәлелдеуді қажет етпейтін негізгі ұсыныстар бар. Бұл аксиомалар. Қалған сөйлемдер олардан шығарылуы керек. Бұл теоремалар. Аристотельдің бұл ғылыми ілімі іс-әрекетке, ең алдымен математикаға басшылық ретінде қабылданды. Шамамен жарты ғасыр өткен соң, Евклидтің "Бастау" атты керемет жұмысы пайда болған кезде, оның құрылымында Аристотель схемасының мөрі айқын көрінді.
2000 жылдан астам уақыт бойы "бастау" батыс және шығыс елдерінде жастар мен ересектердің геометриясын оқыған жалғыз нұсқаулық болды. Бұл адамзат тарихындағы алғашқы ғылыми кітап болды: онда геометрия Аристотель мен Платонға негізделген принциптерге негізделген аксиомалық теория ретінде ұсынылды.
Евклид геометриясын негіздеу жүйесін зерттеушілерге көптеген ғасырлар бойы V постулаты үлкен қызығушылық тудырды. Түзу басқа екі түзумен қиылысқан кезде, олардың қосындысы екі түзуден аз болатын ішкі бір жақты бұрыштар пайда болған кезде, бұл түзулер екі түзуден аз болатын жағымен қиылысады. Оның тұжырымдамасының кеңістігі зерттеушілерді оны дәлелдеуге, басқа постулаттар мен аксиомалардан шығаруға және сол арқылы оны постулаттар қатарынан шығаруға итермеледі.
Мұндай зерттеулер Эллен дәуірінде жүргізілді (Посидоний, б. з. д. I ғ., Санкери, XVIII ғ., Ламберт, XVIII ғ. ) . Бұл геометрияны негіздеу тарихындағы Евклид дәуірі, оның ізбасарлары мен жетілдірушілері дәуірі, геометрияның аңғал-аксиомалық құрылысының кезеңі болды. XIX ғасырдың басында V постулатты дәлелдеудің сәтсіз әрекеттерімен бірге ол аяқталады. Ол керемет ашылуды тудырды - геометрия негіздерін жаңа түсіну және аксиоматикалық әдістің мәнін түсінудегі жаңа қадам.
1826 ж. 11 Ақпанда Қазан университетінің Физика-математика факультетінің отырысында профессор Н. И. Лобачевский (1792-1856 ж. ж. ) Евклидтің V постулаты параллель түзулер теориясының негізінде жатқанын хабарлады. Лобачевскийдің ашылу мәні геометрия үшін өте үлкен. Біріншіден, ол 2000 жылғы геометриялардың алдында тұрған V постулат мәселесін "жауып тастады", бұл V постулат геометрияның қалған аксиомаларына логикалық тұрғыдан тәуелді емес екенін дәлелдеді, яғни олардың қажетті салдары емес. Екіншіден, V постулаты қалған постулаттардан туындамайды, өйткені бұл постулат дұрыс Евклид геометриясымен қатар, V постулаты орындалмайтын тағы бір "қиял" геометриясы мүмкін. Үшіншіден, Лобачевскийдің ашылуы аксиоматикалық әдістің мәніне жаңа көзқарас берді, ол одан әрі дамыды. Аксиомалар өзін-өзі анықтайтын шындық емес. Бұл дәлелдемелерсіз қабылданатын және теорияның негізінде болатын кейбір бастапқы ұғымдар туралы мәлімдемелер, олардан теорияның барлық қосымша тұжырымдары қисынды түрде шығарылады. Шындығында, қабылданған аксиомалардан логикалық түрде дәлелденуі (шығарылуы) мүмкін. Төртіншіден, жаңаның ашылуы, әдетте Евклид емес геометрия деп аталады, Лобачевке дейінгі көзқарасты аяқтады, оған сәйкес Евклид геометриясы кеңістік туралы жалғыз ойлы ілім болып көрінді.
XIX ғасырдың 60-жылдарының аяғында, Лобачевскийдің идеялары математиктердің негізгі бөлігі ретінде танылып, мойындалып, оларды одан әрі дамытуға кіріскен кезде, геометрияның аксиомалық құрылысы мәселесі жаңа күшке ие болды. XIX ғасырдың аяғы мен ХХ ғасырдың басында осы тақырыпта көптеген жұмыстар жарық көрді. 1899 жылы шыққан неміс математигі Д. Гильберттің "Геометрия негіздері" атты шығармасы ең танымал болды. Бұл кітапта Гильберт Евклид геометриясының аксиомаларының толық жүйесін, яғни. геометрияның барлық басқа тұжырымдарын логикалық түрде дәлелдеуге болатын негізгі сөйлемдер жиынтығы осы жүйенің сәйкес еместігін және кейбір аксиомалардың жүйенің қалған аксиомаларынан тәуелсіздігін дәлелдеді. Осы кітаптың жарық көруімен геометрияның логикалық негіздемесі туралы мәселе іс жүзінде жабылды. Сонымен қатар, геометрияны негіздеуге аксиомалық тәсілдің мәнін, сондай-ақ жалпы аксиомалық әдістің мәнін сипаттайтын идеялар мен принциптер ақыры іске асырылды. Аксиоматикалық теорияны құру деген не және қандай сұрақтарға жауап беру керек екендігі қабылданды. Бұл осы теорияның дәйектілігі, толықтығы мен категориясы және оның аксиомалар жүйесінің тәуелсіздігі туралы мәселелер. Әр түрлі бастапқы ұғымдардан шыққан аксиомалардың әртүрлі жүйелері Гильберт кітабы шыққанға дейін (1882 жылы М. Пашем) және ол шыққаннан кейін, 20-жылдардың басына дейін (1916 жылы Г. Вейлем) салынды. Бұл геометрияның аксиомалық негіздемесін абстрактілі-аксиомалық геометрияның құрылысын дамытудың екінші кезеңін аяқтады.
Лобачевский бастаған геометриялық зерттеулер ХХ ғасырдың басында қазіргі математиканың ең іргелі тұжырымдамасы - (математикалық немесе геометриялық) кеңістік ұғымы еркін табиғаттың біртектес объектілерінің (нүктелер, векторлар, фигуралар, функциялар және т. б. ) жиынтығы ретінде пайда болды, олардың арасындағы өзара қатынастар белгілі бір аксиомалар жүйесін қанағаттандырады. Бұл түсінік аксиоматикалық әдіспен ұрықтандырылған геометриялық идеялардың математика, физика және басқа ғылымдардың көптеген салаларына енуіне мүмкіндік берді. Сонымен бірге геометрияның өзі барған сайын дами бастады, математика барған сайын біртұтас ғылымға айналды және оның әр түрлі салаларының, соның ішінде геометрияның шекаралары айқын бола бастады. Математиканың барлық салаларының негізін берік байланыстырған шынымен цемент ерітіндісі ХХ ғасырда математикалық логика болды. Оның көмегімен дәлелдеу процесінің өзі, теоремаларды аксиомалардан шығару процесі зерттелді. Осылайша, аксиоматикалық әдіс одан әрі дамып, белгілі бір мағынада шыңға жетті. Аксиоматикалық теориялардың өзі формальды жүйелер деп аталатын нақты математикалық объектілерге айналды және математикалық әдістермен зерттеле бастады, метатеория деп аталатын математикалық теориялар теориясы (формальды жүйелер теориясы) құрыла бастады. Бұл бағыт Гильберттің еңбектерінде басталды және математиканы формализациялау және негіздеу әдісі деп аталды. Геометрия метатеориясы аясында Евклид геометриясының аксиомалық теориясының, сондай-ақ Лобачевский геометриясының дәйектілігі, категориялылығы, толықтығы мен шешімділігі дәлелденді. ХХ ғасырда аксиоматикалық әдіс дамуының үшінші кезеңі өтті деп айта аламыз.
2. Натурал сандар қатарының әдеттегі моделі
N
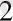 ) аксиомасы бойынша
N
жиынында ешқандай элементтен кейін келмейтін элемент табылады, оны «1» символымен белгілеп, «бір» деп атайды. N
) аксиомасы бойынша
N
жиынында ешқандай элементтен кейін келмейтін элемент табылады, оны «1» символымен белгілеп, «бір» деп атайды. N
 ) аксиомасы бойынша табылатын, 1-ден кейін келетін 1
'
элементін «2» символымен белгілеп, «екі» деп атайды. 3
) аксиомасы бойынша табылатын, 1-ден кейін келетін 1
'
элементін «2» символымен белгілеп, «екі» деп атайды. 3
 салдар бойынша 2≠1 екені белгілі. Осылайша, 2
'
= 3 ( « үш » ),
салдар бойынша 2≠1 екені белгілі. Осылайша, 2
'
= 3 ( « үш » ),
3 ' = 4 ( « төрт » ), т. с. с. белгілеу келісілген.
Бұл элементтердің өзара тең емес екендігіне N
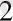 ), N
), N
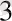 ) аксиомаларын пайдаланып көз жеткізуге болады.
) аксиомаларын пайдаланып көз жеткізуге болады.
Сонымен, N жиынындағы штрих қатынасын граф түрінде былайша беруге болады:
.

 .
.
 .
.
 .
.
 .
. . . ,
.
. . . ,
1 2 3 4 5
ал натурал сандар жиыны
N
былайша жазылады:
N
=
 1, 2, 3, 4, 5, . . .
1, 2, 3, 4, 5, . . .
Математикалық индукция әдісі
N
 ) аксиомасы натурал сандарда математикалық индукция принципі деп аталатын әдісті қолдануға мүмкіндік береді.
) аксиомасы натурал сандарда математикалық индукция принципі деп аталатын әдісті қолдануға мүмкіндік береді.
Теорема (индуктивтік дәлелдеудің дұрыстығы туралы) .
Егер тұжырымдалуы натурал санға байланысты математикалық сөйлем (формула, теорема) 1 натурал саны үшін дұрыс болса, және оны k натурал саны үшін дұрыс деп жорығаннан одан кейін келетін k' саны үшін дұрыс екені шығатын болса, онда ол сөйлем кезкелген натурал сан үшін дұрыс болады.
Теореманы дәлелдемес бұрын оны символдық түрде жазып алайық. Ол үшін мынадай белгілеу енгізейік:
Р(х) - тұжырымдалуы натурал санға байланысты сөйлем болсын, ал оның
а натурал саны үшін дұрыстығын Р( а ) = Т деп жазайық. Онда теорема символдық түрде былайша жазылады:
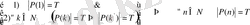
Дәлелдеу. Р(х) сөйлемі дұрыс болатындай натурал сандар жиынын М деп белгілейік:
М =
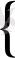 m
m
 N
Р(
m
) = Т
N
Р(
m
) = Т
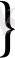 ( * )
( * )
Онда М
 N
болатыны түсінікті. М жиыны N
N
болатыны түсінікті. М жиыны N
 ) аксиомасының А), Б) шарттарын қанағаттандыратынын көрсетейік.
) аксиомасының А), Б) шарттарын қанағаттандыратынын көрсетейік.
Берілгеніндегі 1) шарттан 1
 М екені шығады. Бұл N
М екені шығады. Бұл N
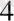 ) аксиомасының А) шарты орындалып тұр деген сөз. Екінші жағынан бұл М≠
) аксиомасының А) шарты орындалып тұр деген сөз. Екінші жағынан бұл М≠
 екенін де көрсетеді. Айталық
k
натурал саны М жиынына тиісті болсын:
k
екенін де көрсетеді. Айталық
k
натурал саны М жиынына тиісті болсын:
k
 М. Онда (*) бойынша Р(
k
) = Т, сондықтан берілгеніндегі 2) шарттан, Р(
k'
) = Т
М. Онда (*) бойынша Р(
k
) = Т, сондықтан берілгеніндегі 2) шарттан, Р(
k'
) = Т
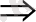
k'
 М. Ал бұл N
М. Ал бұл N
 ) аксиомасының Б) шарты орындалып тұрғанын көрсетеді. Онда N
) аксиомасының Б) шарты орындалып тұрғанын көрсетеді. Онда N
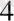 ) аксиомасы бойынша М=
N
, (*) -ны ескерсек,
) аксиомасы бойынша М=
N
, (*) -ны ескерсек,
 n
n
 N
Р(
n
) = Т. ■
N
Р(
n
) = Т. ■
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz