RSA алгоритміне негізделген ақпаратты қорғауды .NET платформасында автоматтандыру


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 46 бет
Таңдаулыға:
КІРІСПЕ
Евклид пен Диофант, Ферма, Эйлер, Гаусс, Чебышев пен Эрмит еңбектерінде диофантты теңдеулерді шешу жөнінде маңызды ойлар жатыр, сол заман үшін үлкен болып саналатын сандардың ең жақын мәнін табу үшін амалдар бар. Соңғы екі он жылдықта криптография мен ЭЕМ-нің кең таралуына байланысты сұраныстың дамуына орай сандар теориясының алгоритмдік сұрақтары даму үстінде. Есептеу машиналары мен электрондық құралдар адамның барлық қызметі мен ой-өрісіне енді. Оларсыз қазіргі заманғы криптографияны елестету мүмкін емес. Мәтінді шифрлеу мен оны бұзуды ЭЕМ көмегімен бүтін сандарды өңдеу ретінде елестетуге болады, бұл амалдар орындалаиын тәсілдер кейбір функциялар секілді бүтін сандардың белгілі бір жиынында орындалады. Мұның бәрі қазіргі заманғы криптографияда сандар теориясының болуына жағдай жасайды. Сонымен қатар, кейбір криптожүйелердің тұрақтылығы тек кейбір сандық -теориялық есептер күрделілігімен негізделеді. Бірақ ЭЕМ мүмкіндігі шекті болып табылады. Ұзын сандық тізбекті белгілі бір өлшемді блоктарға бөлуге тура келеді және әр блокты бөлек шифрлеуге тура келеді. Одан әрі біз барлық шифрленетін сандарды теріс емес және берілген m санынан кіші емес деп санаймыз. Мұндай шектеулер одан әрі шифрлеуден алынатын сандарға да қатысты. Бұл осы сандарды
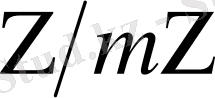 бойынша есептеуге мүмкіндік береді. Шифрленетін функция есептеу сақинасының бір-біріне сыбайлас жүйе ретінде қарастырылынады:
бойынша есептеуге мүмкіндік береді. Шифрленетін функция есептеу сақинасының бір-біріне сыбайлас жүйе ретінде қарастырылынады:
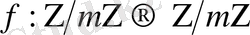
Ал,
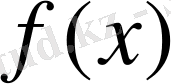 саны шифрленген түрдегі
саны шифрленген түрдегі
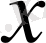 хабарламасын көрсетеді. Мұндай түрдің қарапайым шифры - алмастыру шифры,
хабарламасын көрсетеді. Мұндай түрдің қарапайым шифры - алмастыру шифры,
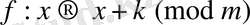 k-бүтін сан үшін болатын көрініске тән. Мұндай шифрды Юлий Цезарь де қолданған. Әрине,
k-бүтін сан үшін болатын көрініске тән. Мұндай шифрды Юлий Цезарь де қолданған. Әрине,
 -тің әрбір көрінісі ақпаратты сақтау үшін қолданылады.
-тің әрбір көрінісі ақпаратты сақтау үшін қолданылады.
1978-жылы американдық Р. Ривест, А. Шамир және Л. Адлеман (R. L. Rivest. A. Shamir. L. Adleman)
 функциясына мысал ұсынды, олар ерекше қасиеттерге ие. Соның негізінде нақты қолданылатын шифрлеу жүйесі алынды, авторлардың есімдерінің алғашқы аттарына сәйкес RSA деп аталды. Бұл функция мынадай:
функциясына мысал ұсынды, олар ерекше қасиеттерге ие. Соның негізінде нақты қолданылатын шифрлеу жүйесі алынды, авторлардың есімдерінің алғашқы аттарына сәйкес RSA деп аталды. Бұл функция мынадай:
- функциясының мәндерін есептейтін әлдеқайда жылдам әдіс бар;
- кері функциясының мәндерін есетейтін жылдам әдіс бар;
- функциясының «құпиясы» бар, егер оны анықтасақ, мәндерін тез есептеуге болады; қарсы жағдайдаесептеуге ауыр, көп уақытты кетіретін, шешуге мүмкін емес есепке айналады.
RSA осы жылдар ішінде ұсынылған ашық кілтті қолданатын алгоритмдер ішінде ең оңай түсінуге және жүзеге асыруға болатын алгоритм.
Бұл дипломдық жұмыс криптографияның ашық кілтті қолданатын алгоритмдердің бірі - RSA-ға арналған.
Осыған орай дипломдық жұмыстың мақсаты - RSA алгоритмін қазіргі таңдағы технологияларды пайдалана отырып, ақпаратты қорғау саласында кеңінен қолдана алатын автоматтандыру жүйесін құру.
Жұмыстың мақсаты дипломдық жұмыс барысында шешілген келесі міндеттерді анықтады:
- Сандар теориясын, оның бөлімдерінің бірі жан сандарды зерттеу. Өте үлкен жай сандарды іздеу
- Екілік жүйедегі сандармен жұмыс жасау
- Ашық және жабық кілттердің құрылымын зерттеу
- Бір компьютерден екінші бір компьютерге ақпаратты шифрлеп жібергенде, барлық қауіпсіздік ережелерін сақтау және зерттеу
Дипломдық жұмыс кіріспеден, төрт бөлімнен, қорытындыдан, әдебиеттер тізімінен және қосымшадан тұрады. Кіріспеде жұмыстың өзектілігі берілген, мақсаты қойылған, сол мақсатқа қол жеткізу міндеттерінен тұрады. Зерттеу объектісі және пәні, оның методологиялық негізі және жұмыстың практикалық маңыздылығы анықталған. Бірінші бөлімде криптографияның негізгі түсініктері мен тарихы, оның жұмыс істеу принциптері мен алгоритмдері, сонымен қатар, RSA алгоритмінде қолданатын математикалық негіздемелер туралы теориялық анықтамалар орын алған. Бірінші бөлімнің басты қорытындысы - криптографияның бастамасын түсіндіру, оның әдістемелері мен алгоритмдерін таныстыру болып табылады. Екінші бөлім ашық кілтті қолданатын алгоритмдерге, соның ішінде, RSA алгоритміне арналған. Үшінші бөлім . NET платформасына, оның құрылымы мен сипаттамасына арналған. Бұл бөлімде C#-тың басқа объектілі-бағытталған программалардан айырмашылығын көрсетілген. Төртінші бөлім жұмыстың қойылымына, яғни бағдарламалық бөлімге арналған. Онда әрбір батырманың мақсатына дейін айтылып кеткен. Ал олардың бағдарламалық кодтары қосымшаларда жазылып кеткен.
Қорытынды бөлімінде дипломдық жұмыс тақырыбы бойынша жалпылама қорытындылар жасалған.
КРИПТОГРАФИЯ НЕГІЗДЕМЕСІ
1 Криптографияның негізгі түсініктемелері мен тарихы
Ақпаратты оны түрлендіру арқылы басқа адам оқи алмайтындай қорғау мәселесі адамзат алдында бұрыннан тұрған мәселелердің бірі болып табылады. Криптография тарихы - адамзат тілінің тарихының замандасы. Оған қоса, жазу алғашқыда криптографиялық жүйе болы табылды, себебі, ежелге қоғамда онымен тек ерекше таңдаулы адамдар ған иелік етті. Ежелгі Египет пен Үндістанның киелі кітаптары соған мысал бола алады. Криптография жазудың кең таралуына байланысты дербес ғылым ретінде қалыптаса бастады.
Криптография тарихын шартты түрде 4 қадамға бөлуге болады:
- жай криптография
- ресми криптография
- ғылыми криптография
- компьютерлік криптография
Жай криптография үшін (XVI ғасыр басына дейінгі кезең) қарсыласты кез келген шифрлік мәтін мазмұнына қатысты шатыстыру тән. Бастапқы қадамда ақпаратты сақтау үшін криптографиямен барабар кодтау және стеганография әдістері қолданды.
Көптеген қолданылатын шифрлар орын ауыстырулар немесе моноалфавиттік ауыстыру арқылы жүзеге асырылды. Жарияланған мысалдардың бірі болып Цезарь шифры табылады, ол мәтіндегі алдыңғы әріпті алфавитте одан алыс тұратын әріпке ауыстыру арқылы жүзеге асырылады. Басқа шифр, полибианды квадрат, грек жазушысы Полибий шығарған, алфавитпен өлшемі 5х5 болатын квадратты кестеге кездейсоқ толтырылатын грек алфавитінің көмегімен жүзеге асатын жалпы моноалфавитті орын ауыстыру болып табылады. Әр әріп квадратта одан төмен тұратын әріппен ауыстырылады.
Ресми криптография қадамы (XVғ. аяғы-XX ғ. басы) криптоанализдің ресми және салыстырмалы түрде тұрақты шифрлерінің пайда болуымен байланысты. Еуропа елдерінде бұл Қайта өрлеу дәуірі кезінде пайда болды, яғни ғылым мен сауданың дамуы ақпаратты қорғаудың әдістері керек болған кезде пайда болды. Бұл қадамдағы маңызды рөлді Леон Батисте Альберти атқарды, ол көп әліппелі орын ауыстыруды алғаш ұсынған итальян архитекторы. XVI ғасырда Блез Вижинер дипломатының атына ие болған бұл шифр берілген мәтінді кілтпен әріпті тізбекті қосу тәсілінен тұрған. Оның «шифр туралы трактат» атты еңбегі криптология жөнінде алғашқы еңбегі болып табылады. Ең алғаш баспа жұмыс болып Иоганн Трисемустың «Полиграфия» (1508 ж. ) еңбегі болып табылады. Ол екі үлкен емес, алайда маңызды жаңалық ашты: полибиандік квадрататы толтыру әдісі және әріп жұптарын шифрлеу.
Көп әліппелі ауыстырудың қарапайым әрі тұрақты әдісі болып XIX ғасырда Чарльз Уитстонмен ашылған Плейфер шифры табылады. Уитстон маңызды жаңалық «екілік квадрат» арқылы шифрлеу әдісін ашты. Плейфер мен Уитстон шифрлары І дүниежүзілік соғысқа дейін қолданылды. XIX ғасырда голландық Керкхофф осы күнге дейін өзекті болып табылатын криптографиялық жүйелердің басты талаптарын ұсынды: шифрлардың құпиялылығы алгоритм емес, кілттің құпиялылығына негізделуі керек. Ғылымға дейінгі оған жоғары криптотұрақтылықпен қамтамасыз ететін криптографияның соңғы сөзі болып шифрларды автоматтандыруға мүмкіндік берген роторлық криптожүйе болды.
Сондай жүйелердің бірі болып 1790-жылы болашақ президент Томас Джефферсонмен жасалынған механикалық машина болды. Көп әліппелі ауыстыру роторлық машина көмегімен бір-біріне қарай айналым жасайтын роторлардың вариациясы арқылы орындалады.
Роторлық машиналар практикалық жағынан сұранысқа XX ғасыр басында ие болды. Алғашқы қолданысқа енген машина болып 1917-жылы Эдвард Хебернмен жасалынып, Артур Кирхпен жаңартылған неміс Enigma машинасы болды. Роторлық машиналар ІІ дүниежүзілік соғыс кезінде кең қолданды. Неміс Enigma машинасынан өзге Sigaba, Турех, Red, Orange, Purple2 қолданды. Роторлық жүйелер- ресми криптографияның шырқау шегі, себебі салыстырмалы түрде тұрақты шифрлар таратты. Роторлық жүйелерге сәтті криптошабуылдар 40-жылдары ЭЕМ-нің пайда болуымен мүмкін болды.
Ғылыми криптографияның айрықша белгісі (XX ғасырдың 30-60-жылдары) - жоғары математикалық негізделген тұрақты криптожүйелердің пайда болуы. 30-жылдардың басына қарай ғылыми криптографияның негізі болып табылатын математика бөлімдері толық қалыптасты: ықтималдықтар теориясы және математикалық статистика, жалпы алгебра, сандар теориясы, алгоритм теориясы, ақпарат теориялары, кибернетика. Ерекше бөлімі болып Клод Шеннонның «Құпия жүйелердегі байланыс теориялары» (1949) атты еңбегі болды, мұнда ақпаратты криптографиялық қорғаудың теориялық принциптері көрсетілген. Шеннон «араласу» және «бөліну» атты ұғымдарды енгізді.
60-жылдарда көшбасшы криптографиялық мектептер блоктық сандар жасауға көшті, олар роторлық криптожүйелермен салыстырғанда аса тұрақты, алайда олар тек сандық электронды құрылымдарды жүзеге асыруды ғана қамтамасыз етті.
Компьютерлік криптография (XX ғасырдың 70-жылдары) өнімділігі криптожүйелерді таратуға жеткілікті, шифрлеудің жоғары жылдамдығын қамтамасыз ететін «қолдық» және «механикалық» шифрлар есептеу машиналардың шығуына байланысты пайда болды.
Криптожүйелердің алғашқы класы болып қолдану кезінде қуатты әрі жинақты есептеу құралдарының пайда болуына байланысты шыққан блоктық шифрлар болды. 70-жылдары шифрлеудің DES американдық стандарты жасалды. Оның авторларының бірі болған Хорст Фейстел, ол блоктық шифрлар моделін сипаттап, соның негізінде жасалынған аса тұрақты симметриялық криптожүйелерді жасады.
DES-тің пайда болуымен криптоанализ байыды, американдық алгоритмдерге шабуыл үшін был криптоанализдің бірнеше тәсілдері жасалды (сызықтық, дифференциалды және т. б. ), практикалық қолданылу жағынан тек есептеу машиналардың пайда болуымен мүмкін болды.
70-жылдардың ортасында қазіргі заманғы криптографияда төңкеріс болды - асимметриялық криптожүйелер пайда болды, ол жақтар арасында бір-біріне құпия кілттің таратылуын қамтамасыз етті. Мұндай негізгі еңбек Уитфилд Диффимен және Мартин Хеллманмен 1976-жылы жарияланған «Қазіргі заманғы криптография бағыттары» болып табылады. Мұнда ең алғаш болып шифрлік ақпараттың кілтсіз таратылу принциптері негізделген болатын. Асимметриялық криптожүйелер идеясына тәуелсіз қатысты Ральф Меркли. Бірнеше жылдардан кейін Рон Ривест, Ади Шамир және Леонард Адлеман RSA жүйесін ашты, ол алғашқы практикалық асимметриялық криптожүйе болып табылады, оның тұрақтылығы үлкен сандардың факторизациясы мәселесіне негізделген. Асимметриялық криптография бірден бірнеше қолданбалы бағыттар ашты, негізінен электронды сандық қолтаңба және электронды ақша.
80-90-жылдары фейстелдік емес шифрлар жасалды (SAFER, RC6), ал 2000-жылы ашық халықаралық сайыстан соң шифрлеудің АҚШ-тың жаңа ұлттық стандарты AES шықты. Соғыстан кейінгі кезеңнен бастап осы күнге дейін есептеу машиналардың пайда болуы криптографиялық әдістердің жаңартылуы мен өңделуін тездетті. Неліктен криптографиялық әдістерді қолдану ақпараттық жүйелердің ең маңызды мәселесі болып отыр?! Бір жағынан, компьютерлік торларда қолдану кеңейді, негізінде, мемлекеттік, әскери, коммерциялық және жеке түрдегі ақпараттың өте үлкен мөлшері таратылатын ғаламдық торап Интернет жүйесін қолдану кеңейді. Басқа жағынан, жаңа қуатты компьютерлердің пайда болуы, жүйелік және нейрондық есептеу технологиясы жақында ғана анықтау мүмкін емес деп саналған криптографиялық жүйелердің дискредитациясына қол жеткізуге мүмкіндік берді. Ақпаратты түрлендіру арқылы қорғау мәселесімен криптология (kryptos - құпия, logos - ғылым) айналысады. Криптология екі бағытқа бөлінеді - криптография және криптоанализ. Бұл бағыттардың мақсаттары қарама-қарсы болып келеді.
Криптография ақпаратты түрлендіруде математикалық әдістерді іздеу және зерттеумен айналысады. Криптоанализдің айналысатын сфералар жүйесі - ақпараттың кілтін білмей шифрын анықтау.
Қазіргі криптография өзіне 4 үлкен бөлімді қосады:
- Симметриялық криптожүйелер.
- Ашық кілтті криптожүйелер.
- Электрондық қолтаңба жүйелері.
- Кілттерді басқару.
Криптографиялық әдістерді қолданудың негізгі мақсаты - байланыс каналдары арқылы жасырын ақпаратты тарату (мысалы, электрондық пошта), жіберілген хабарламалардың ақиқаттығы, шифрлі тұрде ақпаратты сақтау.
Криптографиялық жүйелер қаншалықты қиын және сенімді болғанымен олардың практикалық қолданылуының әлсіз жағы - кілттерді үлестіру мәселесі. Ол үшін ақпараттық жүйелер екі субьекті арасында жасырын ақпарат алмасу мүмкін және кілт солардың біреуімен генерациялану керек, жасырын түрде әрі қарай басқасына жіберілуі керек. Яғни, кілтті тарату үшін криптожүйені қолдану керек. Бұл мәселені классикалық және қазіргі алгебрадан алынған нәтижелер негізінде шешу үшін ашық кілтті жүйелер ұсынылды. Олардың мәні ақпараттық жүйенің әр хабар алушысымен екі кілт генерацияланады, олар бір-бірімен белгілі ережеге сәйкес байланысады. Бір кілт ашық, екіншісі жабық болып жарияланады. Ашық кілт жарияланады және кез-келген хабарлама жібергісі келетін адам үшін белгілі болады. Құпия кілт жарияланбайды.
Бастапқы мәтін хабар алушының ашық кілтімен шифрленіп, оған жіберіледі. Шифрленген мәтіннің негізінен ашық кілтпен шифры анықталу мүмкін емес. Хабарламаны дешифрлеу тек хабар алушыға ғана белгілі болатын жабық кілтті қолдану арқылы ғана мүмкін. Ашық кілтті криптографиялық жүйелер қайта оралмайтын немесе біржақты функциялар деп аталатын ортақ қасиеті бар қызмет атқарады. Берілген х үшін f(x ) мәнін есептеу оңай , алайда тек y = f(x ) болса, х есептеудің оңай тәсілі жоқ.
Біржақты функциялардың көптеген кластары ашық кілтті жүйенің көптүрлілігін тудырады. Алайда біржақты функциялардың барлығы ақпараттық жүйесінде қолдануға жарай бермейді. Қайта оралмайтын деген түсінікте теориялық қайта ораламсыздығы емес, белгіленген уақыт интервалында қазіргі заманғы есептеу құралдарын қолдану арқылы кері мәнін практикалық тұрғыдан есептей алмау айтылады. Сондықтан, ақпаратты тиімді сақтау үшін ашық кілтті жүйелерге екі айқын әрі маңызды талап қойылады:
- Бастапқы мәтіннің түрленуі қайтымсыз болу керек және ашық кілт негізінде қайта қалпына келмеу керек.
- Ашық кілт негізінде жабық кілтті анықтау жаңа технологиялық тұрғыдан мүмкін емес болу керек. Мұнда шифрды анықтауда күрделіліктің төменгі бағасы көрсетілуі керек.
Ашық кілтті шифрлеу алгоритмдері кең қолданысқа ие болды. RSA алгоритмі ашық жүйелер үшін әлемдік де-факто стандарты болды. Қазіргі таңда ұсынылатын ашық кілтті криптожүйелер қайтымсыз түрленудің төмендегідей топтарына жіктеледі:
- Үлкен сандарды көбейткіштерге жіктеу;
- Соңғы өрісте логарифмді есептеу;
- Алгебралық теңдеулердің түбірлерін анықтау.
Ашық кілтті криптожүйелерді 3 түрлі мақсатта қолдануға болады:
- Жіберілген және сақтаудағы мәліметтерді өзіндік қорғау құралы ретінде.
- Кілттерді үлестіру құралы ретінде. Ашық кілтті жүйелер алгоритмдері дәстүрлі криптожүйелермен салыстырғанда аса көп еңбекті қажет етеді.
- Тұтынушыларды аутентификациялау құралы ретінде.
2 Математикалық негіздемелер
2. 1 Күрделілік теориясы
Күрделілік теориясы криптографиялық әдістер мен алгоритмдердің әр түрлі есептеу күрделіліктеріне қарай әдістемелік талдау жасауға мүмкіндік береді. Ол криптографиялық әдістері мен алгоритмдерін салыстыра отырып, оның қаншалықты қауіпсіз екендігін анықтайды.
Алгоритмнің күрделілігі
Алгоритмнің күрделілігі оның орындалуға керекті есептеулік қуаттарымен есептеледі. Есептемелік алгоритмнің күрделілігі мынадай екі параметрмен өлшенеді: T (уақытқа байланысты туындайтын күрделілік) және S(кеңістікке байланысты туындайтын күрделілік немесе жадыға қойылатын талап) . Негізінде, T мен S , n айнымалысына тәуелді функция ретінде қарастырады. Мұндағы, n - бұл қабылданған ақпараттардың шамасы.
Негізінде, есептемелік алгоритмнің күрделілігін О () функциясы арқылы жазады. Бұл күрделілік функциясының жай бөлшектерге жіктеу түрі болып табылады. Мысалы, егер 4 n 2 +7 n +12 алгоритмінің уақытқа байланысты туындайтын күрделілігі болса, есептеулік күрделілігі n 2 болып келеді, оны О(n 2 ) деп белгілейді.
Алгоритмдерді олардың уақыттық немесе кеңістіктік күрделілігіне байланысты жіктейді. Егер алгоритм n -ға тәуелді болмаса, онда ондай алгоритмдерді тұрақты деп атап, О(1) деп белгілейді. Егер уақыттық күрделілігі О(n) болса, онда алгоритмді сызықтық деп атайды. Алгоритмдердің квадраттық, кубтық және тағы да басқа түрлері болады. Бұл алгоритмдердің барлығы - полиноминалды болып келеді, ал олардың күрделілігі О(n m ), мұндағы m - тұрақты шама. Уақыттық күрделілігі бар полиноминалды алгоритмдерді полиноминалды уақыттық алгоритмдер деп атайды.
Күрделілігі О(t f(n) ) есептелетін алгоритмдерді экспоненциалдық алгоритмдер деп атайды, мұндағы t - бірден үлкен тұрақты шама, ал f(n) - белгілі бір полиноминалды функция. Күрделілігі О(с f(n) ) есептелетін экспоненциалдық алгоритмдердің жиынын суперполиноминалды деп атайды, мұндағы с - тұрақты шама, ал f(n) тұрақтыдан қарағанда тездетіп өсетін, бірақ сызықтыдан баяу болатын функция.
3-кесте. n =10 6 шамасындағы әр түрлі алгоритмдердің уақыт күрделілігіне тәуелділігі
Компьютер үшін уақыттың өлшем бірлігі микросекунд болғандықтан, компьютер тұрақты алгоритмдерді - 1 микросекундта, сызықты алгоритмдерді - 1 секундта, ал квадратты алгоритмді - 11. 6 күнде есептей алады екен. Кубтық алгоритмдерді 32000 жылда есептейтін болғандықтан, экспоненциалдық алгоритмдер туралы айтудың қажеті де жоқ.
Шифрленген алгоритмдерді күшпен ашу проблемасын қарастыратып көрейік. Мұндай ашудың уақыттық күрделілігі мүмкін болатын кілттердің санына тура пропорционал. Демек, кілттің ұзындығынан тәуелді деген сөз. Егер n - кілттің ұзындығы болатын болса, онда күшпен салып ашудың күрделілігі О(2 n ) -ге тең.
Проблеманың күрделілігі
Күрделілік теориясы белгілі бір алгоритмді шешудің проблемасын ғана қарастырмайды, сонымен қатар, проблеманың қаншалықты күрделі екенін де анықтайды. Атап айтқанда, сол проблеманы шешуге керекті минималды уақытты және жадының көлемін қарастырады. Оны Тьюринг машинасы деп атайды. Тьюринг машинасы шекзіз жадымен жабдықталған, алгоритмді оқу және жазу үшін арналған есептеудің наңыз моделі болып табылады.
Полиноминалды уақыттық алгоритмдер арқылы шешілетін проблемаларды шешілетін проблемалар деп атайды. Яғни, белгілі ақпарат үшін белгілі уақыт бөлініп, сол уақытта шешіледі. Полиноминалды уақыт ішінде шешілмейтін проблемаларды шешілмейтін деп атайды. Кей жағдайларда, шешілмейтін проблемаларды қиын (ауыр) проблемалар деп те атайды. Алан Тьюринг кейбір проблемаларды шешудің алгоритмін табу мүмкін еместігін дәлелдеді.
Барлық проблемаларды олардың шешілуіне байланысты сәйкесінше кластарға бөлуге болады. Ең маңызды кластар төменде көрсетілген.
Шешілетін проблемалар класы
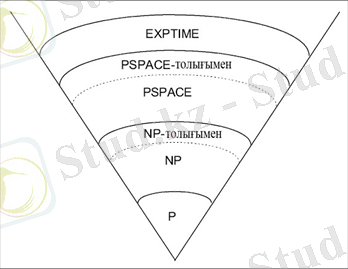
3-сурет
Ең төменде орналасқан Р класы полиномиальды уақытта шешуге болатын барлық мәселелерден тұрады. NP -класы - полиномиальды уақытта тек Тьюрингтің детерминацияланбаған машинасында шешуге болатын барлық мәселелер: жорамал жасай алатын Тьюрингтің қарапайым машинасының нұсқасы. Машина мәселенің шешуін жорамалдай алады- не «сәтті» табу арқылы, не болмаса барлық жорамалдарды параллельды таңдап, барлық жорамалдарды полиномиальды уақытта тексереді.
NP - ның криптографиядағы маңызы: көптеген симметриялық алгоритмдер және ашық кілті бар алгоритмдер детерминацияланбаған полиномиальды уақытта бұзылуы мүмкін. Берілген С шифрлік мәтін үшін криптоаналитик Х ашық мәтінді және к кілтін талғайды және полиномиальды уақытта Х және к арқылы шифрлеу алгоритмін тексере отырып, оның нәтижесі С -ға тең болу мәселесін тексереді. Бұның теориялық маңызы зор, себебі осы алгоритмдердің криптоанализінің күрделілігінің жоғарғы шегін анықтайды. Тәжірибеде бұл әрине полиномиальды уақытта орындалатын детерминацияланған алгоритм, дәл осыны криптоаналитик іздеу тиіс. Бұл алгоритм шифрлердің барлық класстарына бірдей қолданыла алмайды, ол бір қолдануға жарайтын блокноттар үшін жарамайды - кез келген С үшін Х , к көптеген жұптары шифрлеу алгоритмін орындау кезінде С-ны береді, бірақ Х- тің көбісі мәнсіз, мүмкін бола алмайтын ашық мәтіндер болады.
NP - класына Р класы кіреді, себебі полиномиальды уақытта орындалатын Тьюрингтің детерминацияланған машинасында орындалатын кез-келген мәселе полиномиальды уақытта Тьюрингтің детерминацияланбаған машинасында орындала алады, тек жорамалдау сатысы болмайды.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz