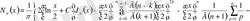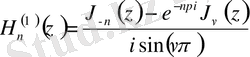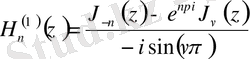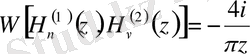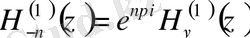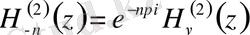Бессель функциялары: теориясы, қатарларға жіктелуі және математикалық физика теңдеулеріндегі қолданылуы


Кіріспе
Қазіргі таңда оқу үрдісінің қай саласын алып қарасақ та оқу-тәрбие жұмысының сапасын арттыру барысында қарқынды жұмыстар атқарылып, жаңа технологиялардың түр-түрі талқыланып жатқан кез.
Қазақстан Республикасының 2011-2020 жылдарға арналған «мемлекеттік білім беруді дамыту» бағдарламасына сәйкес, математикалық білім беру елімізді инновациялық даму жолына алып шығатын маңызды бағыттардың бірі болып табылады.
Жоғарғы оқу орындарында болашақ мамандардың білімінің терең болуын, өз ісіне жауап беретін және нәтижесін бағалай алатын, білімін өздігінен жетілдіріп отыратын, заман талабына сай сұранысқа сәйкес келетін тұлғаны қалыптастыру Қазақстан Республикасының басты мәндеттерінің бірі.
Соңғы жылдары адамзатқа ортақ әртүрлі табиғи, жасанды және т. б. құбылыстар мен олардың үдерістерін байланыстыратын есептерді математикалық модельдеу әдісі арқылы шешу ғылымның көптеген салаларында қолданылып келеді. Бұл тұрғыда математикалық физика теңдеулерінің рөлі өте зор. Себебі, өзгеріс бар жерде оның жылдамдығы, үдеуі және т. б. сипаттамалары өзара қатынаста болады. Ал олардың математикалық баламасы: функция, оның туындылары, олардың бір-бірімен қатынастары, яғни дифференциалдық теңдеулері физика, биология, химия сияқты ғылым салаларында кеңінен қолданылады.
Дифференциалдық теңдеулер теориясынан, шешімдері элементар функциялар интегралынан ақырлы сандар көмегімен өрнектеле алмайтын теңдеулер бар болатыны белгілі, яғни теңдеудің шешімдері бар, бірақ қандай да бір жинақталатын дәрежелік қатарлар түрінде өрнектеледі. Дипломдық жұмыста осындай арнайы функциялар, оның ішінде Бессель функциялары және олардың математикалық физика теңдеулерінде қолданулары қарастырылған.
Бессель теңдеуі деп коэффициенттері айнымалы болатын, мынадай екінші ретті сызықтық дифференциалдық теңдеуді айтамыз:
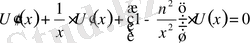
Бұл теңдеу Бессельдің теңдеуі деп аталады, ал оны қанағаттандыратын функциялар, яғни оның интегралдары, Бессельдің функциялары болып табылады. (1) -теңдеу
 -ретті сызықтық теңдеу болғандықтан, оны интегралдау үшін
-ретті сызықтық теңдеу болғандықтан, оны интегралдау үшін
 және
және
 - екі тәуелсіз дербес интегралды білу жеткілікті. Сол кезде сызықтық дифференциалдық теңдеулер теориясы бойынша жалпы интегралы мынадай түрде жазылады:
- екі тәуелсіз дербес интегралды білу жеткілікті. Сол кезде сызықтық дифференциалдық теңдеулер теориясы бойынша жалпы интегралы мынадай түрде жазылады:

Бессельдің дифференциалдық теңдеуіне және оның цилиндрлік немесе Бессель функциялары деп аталатын
 шешімдеріне деген қызығушылық XVIII ғасырдың басында жүйелі түрде басталды. Мұның себебі әр түрлі физикалық есептерді шешу барысында Бессель теңдеуінің туындағанынан пайда болған.
шешімдеріне деген қызығушылық XVIII ғасырдың басында жүйелі түрде басталды. Мұның себебі әр түрлі физикалық есептерді шешу барысында Бессель теңдеуінің туындағанынан пайда болған.
Неміс астрономы, геодезист және математик Ф. В. Бессель (1784-1846)
 арқылы белгіленетін бірінші текті цилиндрлік функциялардың жалғыз түрін зерттеді. Сонымен қатар Ф. В. Бессель
арқылы белгіленетін бірінші текті цилиндрлік функциялардың жалғыз түрін зерттеді. Сонымен қатар Ф. В. Бессель
 функциясының интегралдық теңдігін, рекурренттік қатынастарын тапты;
функциясының интегралдық теңдігін, рекурренттік қатынастарын тапты;
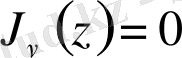 теңдеуінің сансыз көп нөлдер жиынтығының бар екенін дәлелдеді;
теңдеуінің сансыз көп нөлдер жиынтығының бар екенін дәлелдеді;
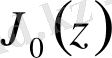 ,
,
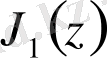 ,
,
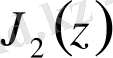 функциялары үшін алғашқы кестелерді құрды.
функциялары үшін алғашқы кестелерді құрды.
Алайда цилиндрлік функциялар теориясының нақты нәтижелері Д. Бернулли, Л. Эйлер және Ж. Лагранж сияқты ғалымдардың еңбектерінен көрінді.
 функциясы Д. Бернуллидің «ауыр тізбектердің тербелісі» атты жұмысында қарастырылған болатын. Сондай-ақ Д. Бернулли
функциясы Д. Бернуллидің «ауыр тізбектердің тербелісі» атты жұмысында қарастырылған болатын. Сондай-ақ Д. Бернулли
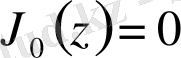 теңдеуінің шексіз түбірлерінің бар екенін анықтады. Л. Эйлердің «Дөңгелек мембрана тербелісін зерттеу» атты жұмысында бүтін
теңдеуінің шексіз түбірлерінің бар екенін анықтады. Л. Эйлердің «Дөңгелек мембрана тербелісін зерттеу» атты жұмысында бүтін
 параметрі үшін цилиндрлік функция теңдеуі алынды. Сол жұмыстарында Л. Эйлер математикалық физикада маңызды рөл атқаратын цилиндрлік функциялардың негізгі нәтижелерін көрсетті.
параметрі үшін цилиндрлік функция теңдеуі алынды. Сол жұмыстарында Л. Эйлер математикалық физикада маңызды рөл атқаратын цилиндрлік функциялардың негізгі нәтижелерін көрсетті.
Уақыт өте келе Вебер немесе Нейман функциялары деп аталатын және
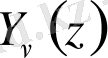 немесе
немесе
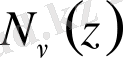 арқылы белгіленетін екінші ретті цилиндрлік функциялар енгізілді. Бұл функциялар
арқылы белгіленетін екінші ретті цилиндрлік функциялар енгізілді. Бұл функциялар
 бірінші ретті цилиндрлік функциялардан сызықтық түрде тәуелсіз болып келеді;
бірінші ретті цилиндрлік функциялардан сызықтық түрде тәуелсіз болып келеді;
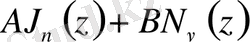 сызықтық комбинациясы Бессель теңдеуінің жалпы шешімін береді. Екінші ретті цилиндрлік функцияларды 1867 жылы К. Нейман ұсынған, алайда олардың теориясы 1879 жылы Г. Вебердің еңбектерінде дамыған деп саналады.
сызықтық комбинациясы Бессель теңдеуінің жалпы шешімін береді. Екінші ретті цилиндрлік функцияларды 1867 жылы К. Нейман ұсынған, алайда олардың теориясы 1879 жылы Г. Вебердің еңбектерінде дамыған деп саналады.
Бессель теңдеуінің екі сызықтық тәуелсіз шешімдерін беретін үшінші ретті цилиндрлік функцияларды 1869 жылы неміс математигі Г. Ханкель ұсынған. Бұл функциялар бірінші және екінші ретті цилиндрлік функциялармен келесі қатынастармен байланысты:
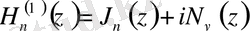 ,
,
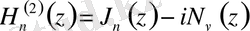
Зерттеу мәселесі. Бессель функциялары, оның қатарға жіктелуі мен математикалық физика теңдеулерінде қолданылуын қарастырып, теориялық білімнің сапасын тереңдету.
Зерттеудің мақсаты : Бессель функциялары мен олардың математикалық физика теңдеулерінде қолданылуын қарастыру.
Зерттеудің болжамы . Егер Бессель функциялары жайлы теориялық білімді нақтылап және олардың қолдануына арналған есептердің шығару жолдарын жүйелеп жүзеге асырсақ, онда зерттеу жұмысының маңыздылығы артады.
Көрсетілген болжамға және алға қойған мақсатқа байланысты келесі зерттеудің міндеттері айқындалады:
- Математикалық физика пәнінің қарастыратын басты мәселелерінің бірі- цилиндрлік функциялар тақырыбын ашу;
- Бессель функцияларының негізгі қасиеттерін келтіру және олардың қатарларға жіктелуін көрсету;
- Бессель функциялары туралы мәліметтерді теориялық жағынан ұғыну және оларды математикалық физика теңдеулерін шешуде қолдану.
Зерттеу жұмысының ғылыми жаңалығы :
- Бессель функциялары және олардың қасиеттерінің теориялық білімі нақтыланды.
- Бессель функциясының дифференциалдық теңдеуі, функцияның қатарларға жіктеу әдістері және оның қолдану аймағы айқындалды.
- Бессель функцияларының қолданылуына арналған есептердің шешу жолдары көрсетілді.
Дипломдық жұмыстың құрылымы : зерттеу жұмысы кіріспеден, төрт бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.
Дипломдық жұмыстың бірінші бөлімінде арнайы функциялар теориясының жалпы теңдеулері келтірілген. Яғни, цилиндрлік функцияның анықтамасы, түрлері, оның ішінде, Бессель, Нейман, Ханкель функциялары туралы айтылған. Әрбір функция қатар ретінде жазылып, дәлелденген. Сонымен бірге,
 және
және
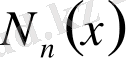 функцияларының графиктері көрсетілген. Ал, екінші бөлімде Бессель дифференциалдық теңдеуінің анықтамасы, Бессель теңдеуінің шешімі мен Бессель функцияларының кейбір қасиеттері, бірінші, екінші және үшінші текті цилиндрлік функциялар қарастырылған. Зерттеу жұмысының үшінші бөлімінде асимптоталық қатарлар мен Бессель функцияларының қатарға жіктелуі көрсетілген. Атап айтқанда, Дини мен Фурье-Бессель қатары, Нейман және Шлёмильх қатарлары дәлелденіп келтірілген. Төртінші бөлімде Бессель функцияларының математикалық физика теңдеулері мен есептерінде қолданулары қарастырылған.
функцияларының графиктері көрсетілген. Ал, екінші бөлімде Бессель дифференциалдық теңдеуінің анықтамасы, Бессель теңдеуінің шешімі мен Бессель функцияларының кейбір қасиеттері, бірінші, екінші және үшінші текті цилиндрлік функциялар қарастырылған. Зерттеу жұмысының үшінші бөлімінде асимптоталық қатарлар мен Бессель функцияларының қатарға жіктелуі көрсетілген. Атап айтқанда, Дини мен Фурье-Бессель қатары, Нейман және Шлёмильх қатарлары дәлелденіп келтірілген. Төртінші бөлімде Бессель функцияларының математикалық физика теңдеулері мен есептерінде қолданулары қарастырылған.
Зерттеу жұмысының нәтижелері бойынша 2019 жылы Павлодар қаласында өткізілген академик Қ. И. Сәтбаевтың 120 жылдығына арналған жас ғалымдар, магистранттар, студенттер мен мектеп оқушыларының «XIX Сәтбаев оқулары» атты халықаралық ғылыми конференциясының материалдарының 12-томында мақала жарияланған болатын.
1. Арнайы функциялар теориясының жалпы теңдеулері
1. 1 Цилиндрлік функцияның анықтамасы, түрлері
Қарапайым арнайы функциялар үшін теңдеулер келесі түрде жазылады:
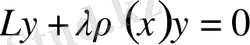 ,
,
 ,
,
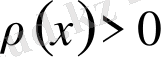 ,
,
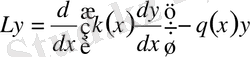 ,
,
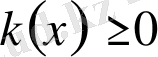 ,
,
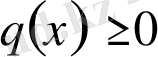 .
.
теңдіктеріне сәйкес келетін
шекаралық шарты тригонометриялық функцияларды анықтайды. Басқа арнайы функциялар үшін теңдеулерді қарастырайық:
1)
Бессель теңдеуі немесе
,
теңдіктерге сәйкес келеді.
2)
кезінде төмендегі Лежандрдың теңдеуін аламыз:
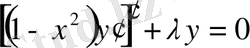
3) Лежандр функцияларының байланысқан теңдеуі:
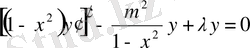
теңдіктеріне сәйкес келеді.
4) Чебышев-Эрмит теңдеуі:
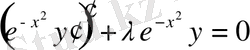 немесе
немесе
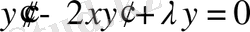
теңдіктеріне сәйкес келеді.
5) Чебышев-Лагерр теңдеуі:
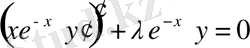 немесе
немесе
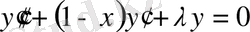
теңдіктеріне сәйкес келеді.
Көрсетілген теңдеулердің сипаттамалық ерекшелігі-
интервалында
коэффициенттерінің нөлге айналып кетуі. Бұл қасиет (1. 1. 1) -теңдеудің шекаралық шарттарын құрастыру барысында маңызды рөл атқарады. [10]
Математикалық физиканың көптеген есептерінің шешімі қарапайым дифференциалдық теңдеуге алып келеді:
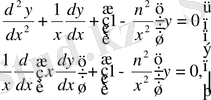
Бұл теңдеу
ретті цилиндрлік функцияның теңдеуі деп аталады.
Цилиндрлік функциялар- цилиндрлік координаталар жүйесіндегі Лаплас, Пуассон, Гельмгольц сияқты математикалық физика теңдеулері үшін айнымалыларды бөлу әдісін қолданып алынған қарапайым дифференциалдық теңдеулердің шешімі болатын бір айнымалылы арнайы функциялардың жалпы атауы болып табылады.
Цилиндрлік функцияларға келтірілетін сипаттамалық шарттар теңдеудің шекаралық шарттары болып табылады:
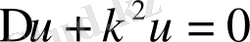
Полярлық координаталарды енгізе отырып, (1. 1. 7) -теңдеуді келесі түрде жаза аламыз:
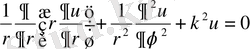
(1. 1. 8) -теңдеуде айнымалыларды бөліп,
алмастыруын енгізсек, сонда:
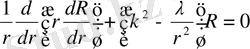
және
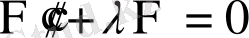 теңдеуі шығады.
теңдеуі шығады.
үшін периодтылық шарты
береді, мұндағы
оң бүтін сан.
деп алып, цилиндрлік функциялар теңдеуін анықтаймыз:
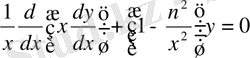 ,
,

немесе
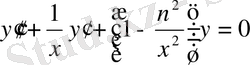 .
.
Әдетте Бессель теңдеуінің шешімдерін цилиндрлік функциялар деп атайды. Цилиндрлік функциялардың
және
кезіндегі тәртібі (асимптоталық тәртібі) оның негізгі қасиеті болып табылады.
Кез-келген цилиндрлік функция
ұмтылған кезіндегі өзінің асимптотикасымен, нақтырақ айтқанда, асимптоталық жіктелудің басты мүшесімен анықталады. [10]
Цилиндрлік функциялардың жиі кездесетін түрлері:
- I және II текті Бессель функциялары
- I және II текті Ханкель функциялары
- Бурже функциялары
- Параболалық цилиндрдің функциялары
- Кельвин функциялары
- Біртекті емес Бессель теңдеуінің дербес шешімдері:
- Ангер функциясы
- Вебер функциясы
- Струве функциясы
- Ломмель функциясы
- I және II текті модифицирленген Бессель функциялары:
- Инфельд функциялары
- Макдональд функциялары
1. 2 Бессель функциясы
 параметрлі Бессель функциясын төмендегі
параметрлі Бессель функциясын төмендегі
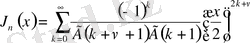 ,
,
қатары арқылы анықтауға болады. Мұндағы
 - гамма функция.
- гамма функция.
(1. 2. 1) -қатардың Бессель функциясы келесі түрде жазылады:
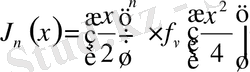 ,
,
бұл жерде
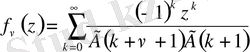 .
.
Даламбер белгісі бойынша
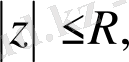
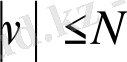 кезінде (1. 2. 2) -қатар бірқалыпты жинақталады.
кезінде (1. 2. 2) -қатар бірқалыпты жинақталады.
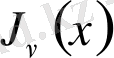 функциясының төмендегі теңдеуді қанағаттандыратынын дәлелдейік:
функциясының төмендегі теңдеуді қанағаттандыратынын дәлелдейік:
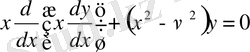 .
.
Ол үшін (1. 2. 1) -қатарды мүшелеп дифференциалдап, құрамында Бессель функциясының туындылары бар өрнектерін есептейміз:
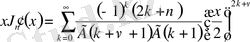 ,
,
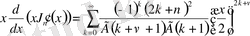 .
.
Сонда
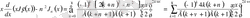 .
.
Гамма-функциясының қасиеті бойынша,
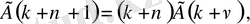
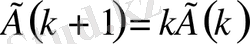 ,
,
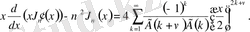
Қосындының айнымалысын
 өзгертетін болсақ, сонда
өзгертетін болсақ, сонда
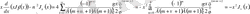
Дәлеліміз тура келді.
 параметрін
параметрін
 -ге алмастырғанда (1. 2. 1) -теңдеу өзгеріссіз қалғандықтан
-ге алмастырғанда (1. 2. 1) -теңдеу өзгеріссіз қалғандықтан
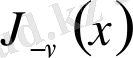 функциясы да сол теңдеудің шешімі бола алады. [3]
функциясы да сол теңдеудің шешімі бола алады. [3]
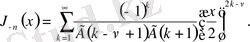
1. 3 Нейман функциясы
 параметрлі Нейман функциясын келесі формула бойынша анықтайық:
параметрлі Нейман функциясын келесі формула бойынша анықтайық:
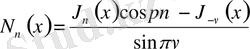 ,
,
 .
.
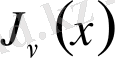 және
және
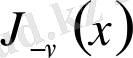 шешімдерінің комбинациясы түрінде Нейман функциясы Бессель теңдеуінің шешімі болатыны анық.
шешімдерінің комбинациясы түрінде Нейман функциясы Бессель теңдеуінің шешімі болатыны анық.
Бүтін емес
 үшін Нейман және Бессель функциялары сызықтық тәуелсіз екенін көрсетейік. Ол үшін функциялардың асимптоталық формулаларын келтірген жеткілікті:
үшін Нейман және Бессель функциялары сызықтық тәуелсіз екенін көрсетейік. Ол үшін функциялардың асимптоталық формулаларын келтірген жеткілікті:
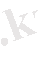
,
.
Осылайша,
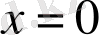 нүктенің айналасында Бессель функциясы шектелген, ал Нейман функциясы шектелмеген болады. Мұндай функциялар сызықтық тәуелді бола алмайды. Сол себепті Бессель теңдеуінің жалпы шешімі:
нүктенің айналасында Бессель функциясы шектелген, ал Нейман функциясы шектелмеген болады. Мұндай функциялар сызықтық тәуелді бола алмайды. Сол себепті Бессель теңдеуінің жалпы шешімі:
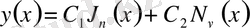 .
.
 (мұндағы
(мұндағы
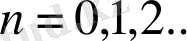 ) алмастыруын енгізгеннен кейін (1. 3. 1) -теңдіктің оң жақ бөлігі
) алмастыруын енгізгеннен кейін (1. 3. 1) -теңдіктің оң жақ бөлігі
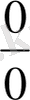 түріндегі анықталмағандықты береді, себебі
түріндегі анықталмағандықты береді, себебі
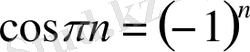 ,
,
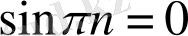 ,
,
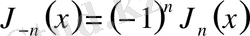 . Алайда бұл анықталмағандық Лопиталь ережесі бойынша шешіледі. Сондықтан
. Алайда бұл анықталмағандық Лопиталь ережесі бойынша шешіледі. Сондықтан
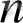 параметрлі Нейман функциясын шек түрінде анықтайық:
параметрлі Нейман функциясын шек түрінде анықтайық:
 .
.
Лопиталь ережесін қолдана отырып
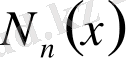 Нейман функциясының өрнегін табайық:
Нейман функциясының өрнегін табайық:
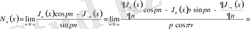
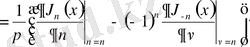 .
.
 болсын. Төмендегі қатарларды
болсын. Төмендегі қатарларды
 параметрі бойынша дифференциалдаймыз:
параметрі бойынша дифференциалдаймыз:
,
.
Сонда
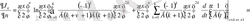
;

.
 болса, сонда
болса, сонда
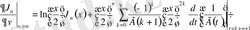 ;
;
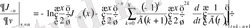 .
.
(1. 3. 6) -формулада қатардың алғашқы
 мүшелерін таңдап алып және
мүшелерін таңдап алып және
 теңдеуін қолданып жазайық. Нәтижесінде
теңдеуін қолданып жазайық. Нәтижесінде
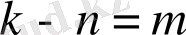 алмастыруын енгізіп, қорытындылаймыз:
алмастыруын енгізіп, қорытындылаймыз:
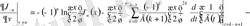
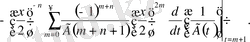
 ;
;
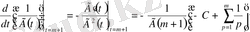 ,
,

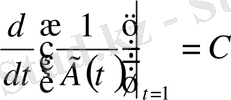 ;
;
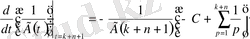 .
.
(1. 3. 11) -теңдікті (1. 3. 5) -ке, ал (1. 3. 8) және (1. 3. 10) -теңдіктерді (1. 3. 7) -теңдеугеге енгізсек, сонда:
;
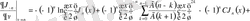
.
Осыдан шығатыны
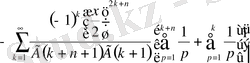 .
.
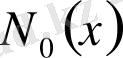 функциясының қатарға жіктелуі (1. 3. 12) -формуладан шығады. Егерде ол жерге
функциясының қатарға жіктелуі (1. 3. 12) -формуладан шығады. Егерде ол жерге
 алмастыруын енгізетін болсақ, сонда:
алмастыруын енгізетін болсақ, сонда:
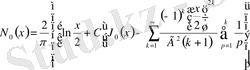 .
.
 кезінде (1. 3. 12), (1. 3. 13) -теңдіктерінен Нейман функциясы үшін келесі асимптоталық формулалар шығады
кезінде (1. 3. 12), (1. 3. 13) -теңдіктерінен Нейман функциясы үшін келесі асимптоталық формулалар шығады
,
;
.
Көріп отырғанымыздай,
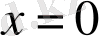 нүктенің маңайында Нейман функциясы шектелмеген. Сол себепті Бессель теңдеуінің жалпы шешімін (1. 3. 2) -теңдігі түрінде жазуға болады. Төменде берілген графиктерден (график 1. 3. 1 және 1. 3. 2) -
нүктенің маңайында Нейман функциясы шектелмеген. Сол себепті Бессель теңдеуінің жалпы шешімін (1. 3. 2) -теңдігі түрінде жазуға болады. Төменде берілген графиктерден (график 1. 3. 1 және 1. 3. 2) -
 және
және
 функцияларының шексіз көп түбірлері бар екені көрініп тұр. [1], [3]
функцияларының шексіз көп түбірлері бар екені көрініп тұр. [1], [3]

График 1. 3. 1-
-тің оң мәнінде
және
функцияларының графиктері
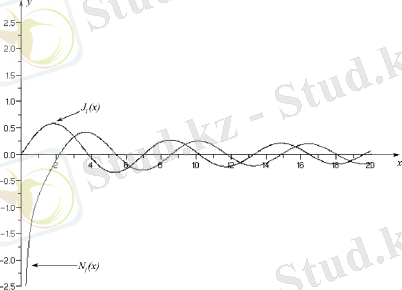
График 1. 3. 2-
-тің оң мәнінде
және
функцияларының графиктері
1. 4 Ханкель функциясы
Келтірілген Бессельдің бірінші текті функциясынан басқа Бессель теңдеуінің шешімі бола алатын функциялар баршылық. Олардың ішінде Ханкельдің бірінші және екінші ретті арнайы функциялары:
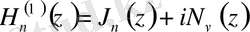 - бірінші текті Ханкель функциясы
- бірінші текті Ханкель функциясы
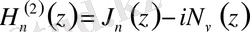 - екінші текті Ханкель функциясы
- екінші текті Ханкель функциясы
Мұндағы
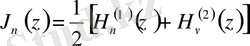 - бірінші ретті Бессель функциясы
- бірінші ретті Бессель функциясы
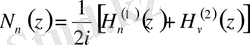 - Нейман функциясы
- Нейман функциясы
Бұл формулалардың Ханкель, Бессель және Нейман функцияларымен байланысы тәуелсіз аргументті косинус функциясының синуспен байланысына ұқсас болып келеді.
Сонымен қатар индексі
 -ге тең Ханкель функциялары Гельмгольц теңдеуінің фундаменталь шешіміне айналып кетеді.
-ге тең Ханкель функциялары Гельмгольц теңдеуінің фундаменталь шешіміне айналып кетеді.
Ханкель функциясы (үшінші текті Бессель функциялары) - бұл бірінші және екінші текті Бессель функцияларының сызықты комбинациясы, демек Бессель теңдеуінің шешімі болып табылады. Ханкель функциялары атақты неміс математигі Герман Ханкельдің құрметіне аталған.
Ханкель функцияларының кейбір қасиеттері:
- Бірінші текті Бессель функциялары арқылы бейнеленуі:
- Вронский анықтауышы арқылы бейнеленуі:
- Индекстері бойынша симметриялы түрде бейнеленуі:
- Асимптоталық көріністері:
~
, егер
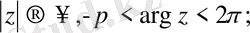
~
, егер
, [1]
2. Бессельдің дифференциалдық теңдеуі. Бессель функцияларының кейбір қасиеттері
2. 1 Бессельдің дифференциалдық теңдеуі. Бессель теңдеуінің шешімі. Бірінші текті цилиндрлік функциялар
Цилиндрлік және сфералық координаталарды қолдануды қарастыратын математикалық физиканың көптеген есептерінде айнымалыларды бөлу процесі келесі дифференциалдық теңдеуге әкеледі:
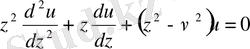 ,
,
(2. 1. 1) -теңдеу Бессель теңдеуі деп аталады, ал оның шешімі цилиндрлік немесе Бессель функциялары болып табылады. (2. 1. 1) -теңдеу II-ретті сызықтық дифференциалдық теңдеу болғандықтан, оның жалпы интегралы
 түрінде жазылады. Мұндағы
түрінде жазылады. Мұндағы
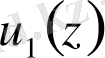 ,
,
 - (2. 1. 1) -теңдеуінің сызықтық тәуелсіз дербес шешімдері. [5], [9]
- (2. 1. 1) -теңдеуінің сызықтық тәуелсіз дербес шешімдері. [5], [9]
(2. 1. 1) -теңдеуінің шешімін
 аргументінің өспелі дәрежелері арқылы жалпыланған дәрежелік қатары түрінде іздейміз:
аргументінің өспелі дәрежелері арқылы жалпыланған дәрежелік қатары түрінде іздейміз:
 .
.
Бұл жерде (2. 2. 2) -қатарының
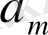 коэффициенттерін және
коэффициенттерін және
 -ны анықтайық. Ол үшін (2. 2. 2) -қатарының бірінші және екінші ретті туындыларын тауып, (2. 1. 1) -теңдеуінің сол жақ бөлігіне, яғни
-ны анықтайық. Ол үшін (2. 2. 2) -қатарының бірінші және екінші ретті туындыларын тауып, (2. 1. 1) -теңдеуінің сол жақ бөлігіне, яғни
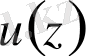 функциясының орнына қоямыз:
функциясының орнына қоямыз:
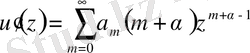 ,
,
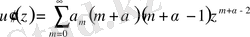 .
.
Нәтижесінде (2. 1. 1) -теңдеуінің алғашқы дербес шешімін келесі түрде аламыз:
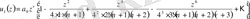 ;
;
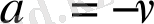 болғандағы, (2. 1. 1) -теңдеуінің екінші дербес шешімі:
болғандағы, (2. 1. 1) -теңдеуінің екінші дербес шешімі:
 .
.
Әдетте
 және
және
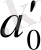 тұрақтыларына келесі мәндер беріледі:
тұрақтыларына келесі мәндер беріледі:
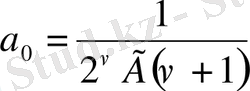 ,
,
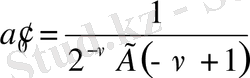 .
.
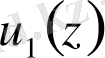 алғашқы қатары Бессель немесе I-ретті цилиндрлік функция деп аталатын функцияны анықтайды. Басқаша айтқанда
алғашқы қатары Бессель немесе I-ретті цилиндрлік функция деп аталатын функцияны анықтайды. Басқаша айтқанда
 бойынша алынған
бойынша алынған
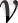 индексінің Бессель функциясы
индексінің Бессель функциясы
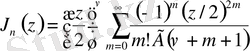 ,
,
мұндағы
 - гамма функция.
- гамма функция.
Бессель функциясының графигі тербелістері
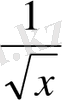 -ке пропорционал түрде өшетін синусоидаға ұқсас болып келеді. Төмендегі берілген суретте (Сурет 2. 1)
-ке пропорционал түрде өшетін синусоидаға ұқсас болып келеді. Төмендегі берілген суретте (Сурет 2. 1)
 үшін
үшін
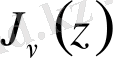 функциясының графигі көрсетілген:
функциясының графигі көрсетілген:
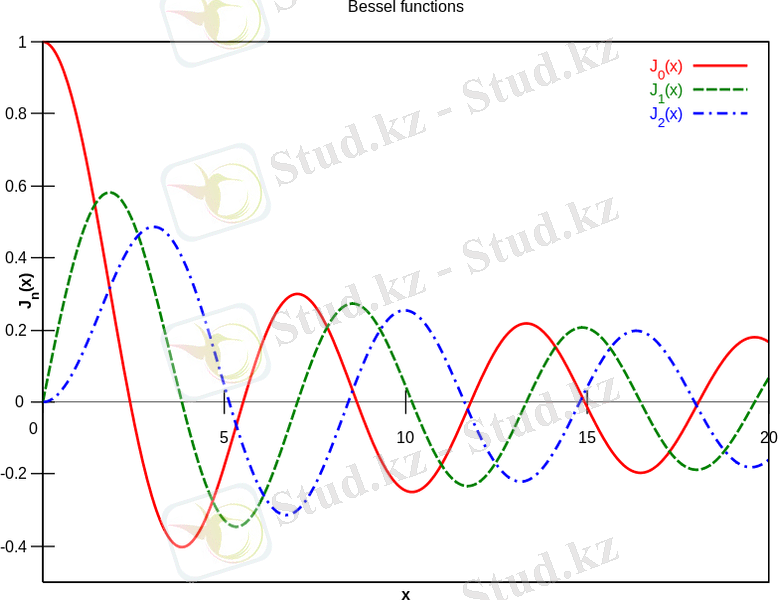
Сурет 2. 1
Екінші қатары
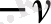 теріс индексінің Бессель функциясын анықтайды:
теріс индексінің Бессель функциясын анықтайды:
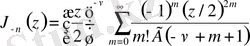 .
.
Индексі бүтін емес сан кезінде
және
функциялары сызықтық тәуелсіз болатыны белгілі. Егер
- болса, онда
және
функциясын келесі түрде жазуға болады:
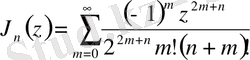 .
.
Бұл жағдайда
және
функциялары арасында төмендегі тәуелділік орын алады:
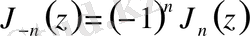 .
.
мүшесінен бастап (2. 1. 4) -теңдеуді қайтадан жазатын болсақ:
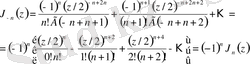
аламыз. [6]
2. 2 Екінші және үшінші текті цилиндрлік функциялар
Индексі бүтін сан емес Бессель теңдеуінің жалпы шешімін келесі түрде жазуға болады:
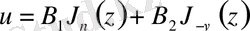 .
.
Әлбетте, бұл жағдайда шешімі ретінде
 функциясы бола алады. Мұндағы
функциясы бола алады. Мұндағы
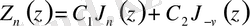 . Осы жерде
. Осы жерде
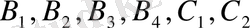 -
-
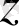 аргументінен тәуелсіз;
аргументінен тәуелсіз;
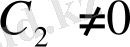 .
.
Егер
 ,
,
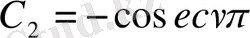 қойсақ, онда
қойсақ, онда
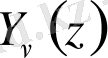 арқылы белгіленетін функцияны аламыз:
арқылы белгіленетін функцияны аламыз:
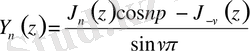 .
.
Кейбір әдебиетте ол Нейман функциясы деп жазылады және
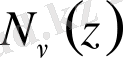 арқылы белгіленеді.
арқылы белгіленеді.
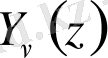 функциясы Бессель функциясы немесе
функциясы Бессель функциясы немесе
 бойынша алынған
бойынша алынған
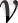 индексінің II-ретті цилиндрлік функциясы деп те аталады.
индексінің II-ретті цилиндрлік функциясы деп те аталады.
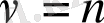 бүтін мәнінде (2. 2. 1) -теңдеуінің оң жақ бөлігі анықталмағандықтың
бүтін мәнінде (2. 2. 1) -теңдеуінің оң жақ бөлігі анықталмағандықтың
 түріне айналып кетеді.
түріне айналып кетеді.
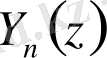 табу үшін анықталмағандықты Лопиталь ережесі бойынша анықтаймыз. Нәтижесінде келесі формула пайда болады:
табу үшін анықталмағандықты Лопиталь ережесі бойынша анықтаймыз. Нәтижесінде келесі формула пайда болады:
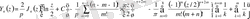
Мұндағы
 - Эйлер тұрақтысы; Оның жуықтап алғандағы мәні
- Эйлер тұрақтысы; Оның жуықтап алғандағы мәні

 .
.
Бессель теңдеуінің жалпы интегралы
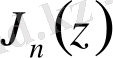 және
және
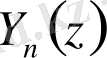 функциялары арқылы өрнектелсе де, кейбір мәселелерде Бессель теңдеуінің басқа интегралдарын қолданған ыңғайлы. Сызықтық дифференциалдық теңдеулер теориясы негізінде бұл интегралдар
функциялары арқылы өрнектелсе де, кейбір мәселелерде Бессель теңдеуінің басқа интегралдарын қолданған ыңғайлы. Сызықтық дифференциалдық теңдеулер теориясы негізінде бұл интегралдар
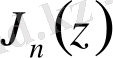 және
және
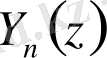 функцияларының сызықтық комбинациясы болуы керек. Келесі теңдіктерді қарастырайық:
функцияларының сызықтық комбинациясы болуы керек. Келесі теңдіктерді қарастырайық:
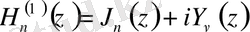 ,
,
 ,
,
Берілген функциялар III-ретті цилиндрлік функциялар деп аталады. Сәйкесінше оларды I және II ретті Ханкель функциялары деп те атайды.
(2. 2. 3) -теңдеуде көрсетілгендей, Ханкель, Бессель және Нейман функциялары арасындағы тәуелділік тәуелсіз аргументті косинус функциясының синуспен байланысына ұқсас болып келеді. [6]
Егер толқынды теңдеуді интегралдау есебінде толық аргументті Бессель функциясы бойлық толқынның бейнесін берсе, Ханкель функциялары көлденең таралған толқынның бейнесін көрсете алады. Шексіз аймақтағы толқындық процестерді зерттеу саласында Ханкель функциялары қаншалықты маңызды рөл атқаратыны көрініп тұр. [10]
2. 3 Бессель теңдеуіне келтірілетін дифференциалдық теңдеулер
Бұл бөлімде жаңа айнымалыларды енгізу арқылы Бессель теңдеуіне келтірілетін теңдеулер көрсетіледі. Келесі түрдегі теңдеуді қарастырайық:
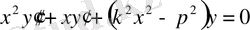
мұндағы
 - нөлден өзге тұрақты сан.
- нөлден өзге тұрақты сан.
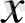 - тің орнына жаңа
- тің орнына жаңа
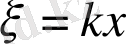 тәуелсіз айнымалыны енгізейік. Сонда
тәуелсіз айнымалыны енгізейік. Сонда
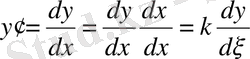 және
және
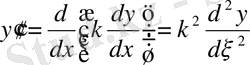 ,
,
Осыдан (2. 3. 1) -теңдеу:
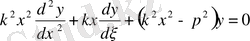 ,
,
немесе
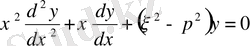 .
.
Бұл тәуелсіз айнымалысы
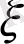 болатын Бессель теңдеуі деп аталады.
болатын Бессель теңдеуі деп аталады.
Осылайша (2. 3. 1) -теңдеудің жалпы интегралы келесідей жазылады:
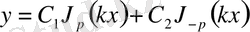
Ал, егер
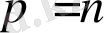 бүтін оң сан немесе 0 болса, сонда
бүтін оң сан немесе 0 болса, сонда
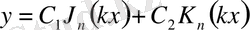 .
.
Бессель теңдеуіне келтірілетін теңдеулер классына қосымша мысал келтірейік. Ол үшін төмендегі теңдеуге жаңа
 айнымалыны және жаңа
айнымалыны және жаңа
 функциясын енгізейік.
функциясын енгізейік.
 ,
,
 және
және
 ,
,
мұндағы
 -тұрақтылар.
-тұрақтылар.
(2. 3. 5) -теңдіктерді дифференциалдасақ, сонда
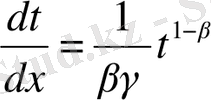 ,
,
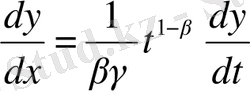 ,
,

Сонымен қатар,
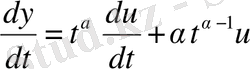 ,
,
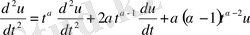 .
.
 теңдіктерін (2. 3. 4) -теңдеуге апарып қойып және
теңдіктерін (2. 3. 4) -теңдеуге апарып қойып және
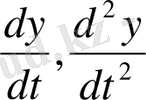 өрнектерін
өрнектерін
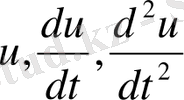 теңдіктерімен алмастыратын болсақ, сонда
теңдіктерімен алмастыратын болсақ, сонда
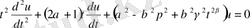
Осылайша, (2. 3. 6) -теңдеудің жалпы интегралы келесі түрде жазылады:
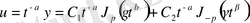 ,
,
Егер
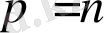 - бүтін оң санға немесе нөлге тең болса, онда
- бүтін оң санға немесе нөлге тең болса, онда
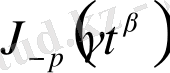 -ны
-ны
 өрнегімен алмастыру қажет.
өрнегімен алмастыру қажет.
(2. 3. 6) -теңдеу төмендегі теңдеудің бір түрі болып табылады
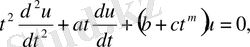
мұндағы
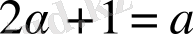 ,
,
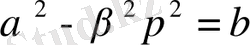 ,
,
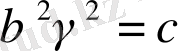 ,
,
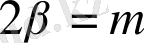 .
.
Егер
 немесе
немесе
 нөлге тең болса, онда (2. 3. 9) -теңдеу Эйлер теңдеуі деп аталады.
нөлге тең болса, онда (2. 3. 9) -теңдеу Эйлер теңдеуі деп аталады.
(2. 3. 9) -теңдеуінің дербес жағдайын қарастырайық:
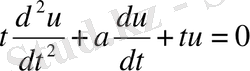
Теңдеуді
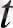 -ға көбейтсек,
-ға көбейтсек,
 кез-келген сан,
кез-келген сан,
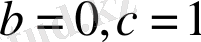 және
және
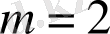 болатынын көреміз.
болатынын көреміз.
Осыдан (2. 3. 9) -теңдіктер келесі түрде жазылады:
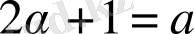 ,
,
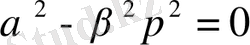 ,
,
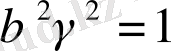 ,
,
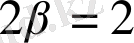 ,
,
мұндағы
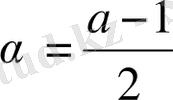 ,
,
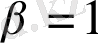 ,
,
 ,
,
 ,
,
және (2. 3. 7) -теңдікке сәйкес (2. 3. 10) -теңдеуінің жалпы интегралы:
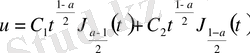 .
.
Атап айтқанда, (2. 3. 8) -теңдеу қолданыста жиі кездесетін, жалпы интегралы Бессель функциялары арқылы өрнектелетін сызықтық теңдеулердің кең ауқымды түрлерін береді. [6], [9]
3. Бессель функциялары бойынша қатарлардың жіктелуі. Асимптоталық қатарлар
3. 1 Көрсеткіштік қатардың Бессель функциялары бойынша жіктелуі. Сонин бойынша қатардың жіктелуі
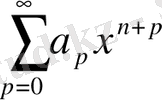 шексіз қатарын қарастырайық. Егер
шексіз қатарын қарастырайық. Егер
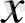 -тің әрбір дәрежесінің орнына оның Бессель функциялары бойынша жіктелуін жазатын болсақ, онда келесі түрдегі теңдікті аламыз:
-тің әрбір дәрежесінің орнына оның Бессель функциялары бойынша жіктелуін жазатын болсақ, онда келесі түрдегі теңдікті аламыз:
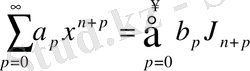
мұндағы

Егер
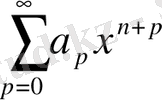 қатары абсолют жинақталған болса, онда (3. 1. 1) -теңдік орындалады және
қатары абсолют жинақталған болса, онда (3. 1. 1) -теңдік орындалады және
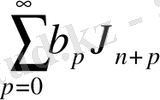 қатары да жинақталатын болады. Алдымен (3. 1. 1) -теңдіктің
қатары да жинақталатын болады. Алдымен (3. 1. 1) -теңдіктің
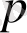 -жұп болатын мүшелерін қарастырайық.
-жұп болатын мүшелерін қарастырайық.
Қосындыларды
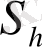 және
және
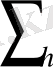 арқылы белгілейік
арқылы белгілейік
 және
және
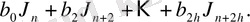
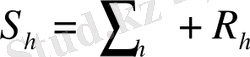 ,
,
мұндағы
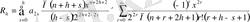 .
.
 ,
,
мұндағы
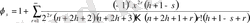 .
.
Сонымен бірге,
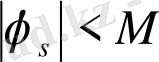 ,
,
Бұл жерде
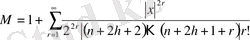 .
.
Осыдан шығатыны
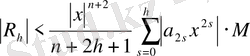 .
.
Бірақ
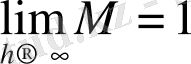 ; сондықтан да
; сондықтан да
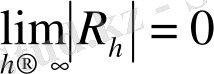 .
.
Осылайша
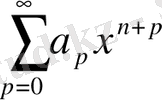 қатарының
қатарының
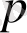 -тақ болатын мүшелерінің қосындысы
-тақ болатын мүшелерінің қосындысы
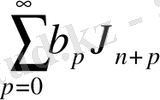 қатарының
қатарының
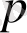 -тақ болатын мүшелерінің қосындысына тең екенін көрсетуге болады. Демек, осы екі қатар бір-біріне тепе-тең болып келеді.
-тақ болатын мүшелерінің қосындысына тең екенін көрсетуге болады. Демек, осы екі қатар бір-біріне тепе-тең болып келеді.
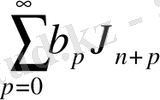 қатары
қатары
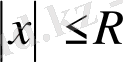 болғанда, біркелкі жинақталады; мұндағы
болғанда, біркелкі жинақталады; мұндағы
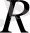 -
-
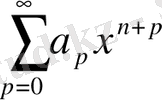 қатарының жинақталу радиусынан кіші.
қатарының жинақталу радиусынан кіші.
Төменде жазылған келесі бір жіктелуді қарастырайық:
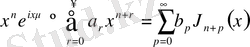 .
.
Бұл жерде
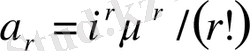
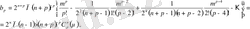
мұндағы
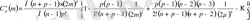
Осыдан
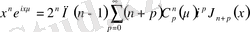 .
.
Берілген теңдеуге
 енгізейік; Төмендегі шыққан теңдеу Сонин бойынша қатардың жіктелуі деп аталады; [4]
енгізейік; Төмендегі шыққан теңдеу Сонин бойынша қатардың жіктелуі деп аталады; [4]
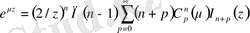
3. 2 Қосу теоремасы және оның жалпыланған түрі
Төмендегі берілген теңдікті қарастырайық:
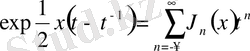
Осыдан
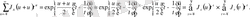
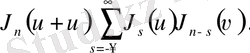
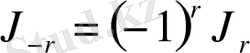 болғандықтан,
болғандықтан,
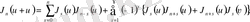
Салдар I.

Салдар II.
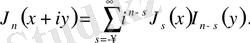
Бұл теңдіктен
 жұп немесе тақ болатын мүшелерді бөлу арқылы
жұп немесе тақ болатын мүшелерді бөлу арқылы
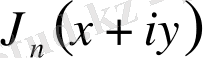 функциясының нақты не жорамал бөлігін алуға болады. [2]
функциясының нақты не жорамал бөлігін алуға болады. [2]
Енді Нейманға тиесілі қосу теоремасының жалпыланған түрін қарастырайық.
(3. 2. 1) -теңдіктен шығатыны
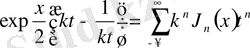 .
.
Бірақ та
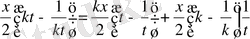 ,
,
Сондықтан
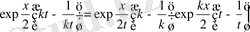 .
.
Демек,
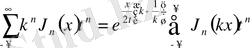 .
.
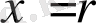 ,
,
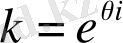 енгізсек, сонда
енгізсек, сонда
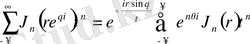 .
.
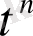 - бар коэффициенттерін теңестірсек, сонда
- бар коэффициенттерін теңестірсек, сонда
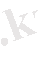
 ,
,
мұндағы

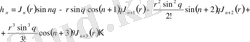
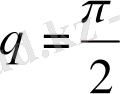 етіп алсақ, сонда
етіп алсақ, сонда
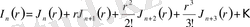
(3. 2. 5) -теңдікке апарып қойсақ, сонда

қатары шығады.
Теңдіктің сол жақ бөлігі
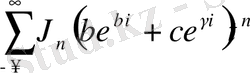
-ге тең болады.
Егер теңдіктің оң жақ бөлігі
 дәрежелік қатарына жіктелсе, онда
дәрежелік қатарына жіктелсе, онда
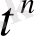 -ның алдындағы коэффициент
-ның алдындағы коэффициент
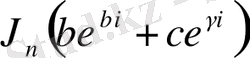 келесі түрде өрнектеледі:
келесі түрде өрнектеледі:
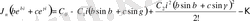
мұндағы
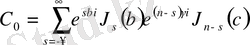 .
.
Алайда, бұл формула практикалық мақсатта тым күрделі болғандықтан,
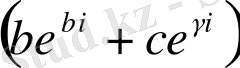 - нақты санға тең болатын жағдайын егжей-тегжейлі қарастырамыз. Ол үшін
- нақты санға тең болатын жағдайын егжей-тегжейлі қарастырамыз. Ол үшін
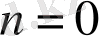 тең деп аламыз.
тең деп аламыз.
Егер
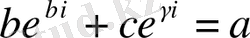 болса, онда
болса, онда
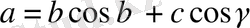 және
және
 ;
;
сол үшін
 .
.
Егерде
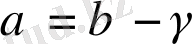 деп жазсақ, онда (3. 2. 9) -теңдіктегі жалпы формуланың дербес жағдайы келесі түрде жазылады:
деп жазсақ, онда (3. 2. 9) -теңдіктегі жалпы формуланың дербес жағдайы келесі түрде жазылады:
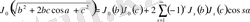 .
.
Егерде
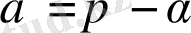 болса, сонда (3. 2. 9) -формула келесі түрде жазылады:
болса, сонда (3. 2. 9) -формула келесі түрде жазылады:
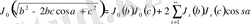 .
.
Бұл формула Нейманның нәтижесімен сәйкес келеді.
Ал егер (3. 2. 9) -формулада
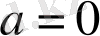 теңестіріп алсақ, сонда (3. 2. 1) - қосу формуласы шығады. [4]
теңестіріп алсақ, сонда (3. 2. 1) - қосу формуласы шығады. [4]
3. 3 Бессельдің бірінші және екінші интегралдары
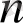 -нің бүтін мәндерінде
-нің бүтін мәндерінде
 функциясы арнайы анықталған интеграл ретінде көрсетілуі мүмкін. Ол үшін келесі мысалды қарастырайық:
функциясы арнайы анықталған интеграл ретінде көрсетілуі мүмкін. Ол үшін келесі мысалды қарастырайық:
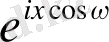 функциясы периоды
функциясы периоды
 -ге тең
-ге тең
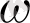 -ға қатысты жұп функция болсын. Фурье қатарының теориясы бойынша ол еселі бұрыштардың косинустары бойынша орналасқан Фурье қатарына жіктелуі керек. Атап айтқанда, төмендегі теңдік орындалуы қажет.
-ға қатысты жұп функция болсын. Фурье қатарының теориясы бойынша ол еселі бұрыштардың косинустары бойынша орналасқан Фурье қатарына жіктелуі керек. Атап айтқанда, төмендегі теңдік орындалуы қажет.
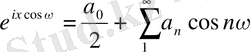 ,
,
мұндағы
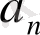 коэффициенті келесі формуламен:
коэффициенті келесі формуламен:
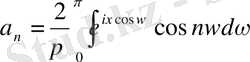
анықталады.
 ,
,
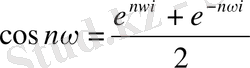
 жаңа айнымалыны енгізсек, (3. 3. 1) -теңдік келесі түрде жазылады:
жаңа айнымалыны енгізсек, (3. 3. 1) -теңдік келесі түрде жазылады:
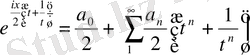 .
.
немесе:
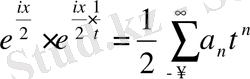 .
.
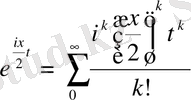
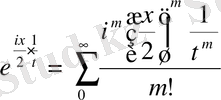 .
.
Осы қатарларды көбейтіп, ықшамдағаннан кейін
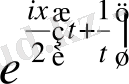 шамасының
шамасының
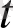 дәрежесі бойынша жіктелетінін көреміз.
дәрежесі бойынша жіктелетінін көреміз.
Осыдан
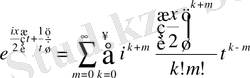
теңдігі шығады.
Егерде
 , яғни егер
, яғни егер
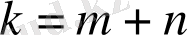 , мұндағы
, мұндағы
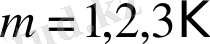 , сонда теңдеудің оң жақ бөлігінде
, сонда теңдеудің оң жақ бөлігінде
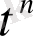 шығады. Сонымен
шығады. Сонымен
 . Сондықтан да (3. 3. 7) -теңдеуді төмендегідей түрде жазуға болады:
. Сондықтан да (3. 3. 7) -теңдеуді төмендегідей түрде жазуға болады:
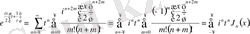
Шыққан теңдеуді (3. 3. 3) және (3. 3. 2) -теңдіктерімен салыстырып отырсақ, сонда
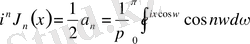
Тақ және жұп функция интегралдарының қасиеті бойынша келесі теңдіктер орындалуы тиіс:
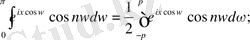
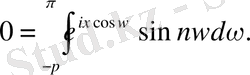

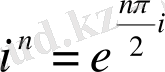 болғанда,
болғанда,
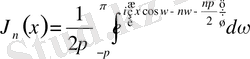
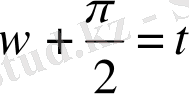 болғанда,
болғанда,
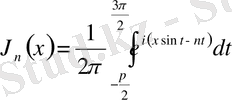

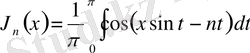 (оң және бүтін
(оң және бүтін
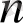 саны үшін)
саны үшін)
Бұл Бессель ойлап тапқан интеграл болып табылады. [6]
Біз
 -нің тек оң бүтін мәндерінде орындалатын
-нің тек оң бүтін мәндерінде орындалатын
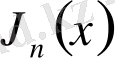 функциясының анықталған интеграл түрінде жазылған өрнегін қарастырған едік.
функциясының анықталған интеграл түрінде жазылған өрнегін қарастырған едік.
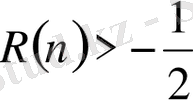 шартын қанағаттандыратын Бессельге төмендегі жазылған формула да тиесілі
шартын қанағаттандыратын Бессельге төмендегі жазылған формула да тиесілі
 .
.
Оны дәлелдеу үшін
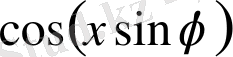 функциясын
функциясын
 -тің өспелі дәрежелері арқылы жіктейік, сонда
-тің өспелі дәрежелері арқылы жіктейік, сонда

Бірақ та
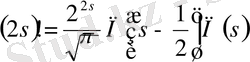 ;
;
Сондықтан (3. 3. 15) -теңдіктің оң жақ бөлігі:
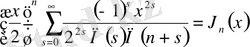 .
.
Егер
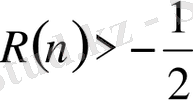 кезінде (3. 3. 1) -формулаға
кезінде (3. 3. 1) -формулаға
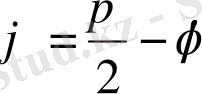 енгізетін болсақ, сонда
енгізетін болсақ, сонда
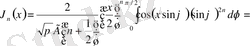
 ,
,
Бірақ
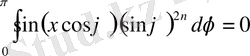 ,
,
Сондықтан
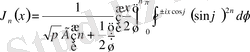 .
.
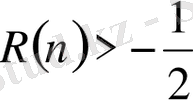 шартын қанағаттандыратын келесі формулаларды (3. 3. 18) -теңдіктен шығарып алуға болады:
шартын қанағаттандыратын келесі формулаларды (3. 3. 18) -теңдіктен шығарып алуға болады:
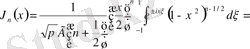
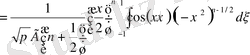 ;
;
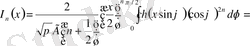

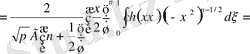
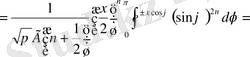
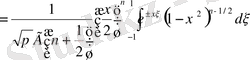 . [4]
. [4]
... жалғасы3. 4 Асимптоталық қатардың Бессель функциялары бойынша жіктелуі
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz