Больцман таралуы

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

Қарағанды-2020ж

Мазмұны

I. Кіріспе

II. Негізгі бөлім

II. 1. Молекулалар жылдамдық бойынша таралуы

II. 2. Максвел таралу заңы

II. 3. Больцманның таралу заңы

III. Қорытынды

Кіріспе

Молекулалық-кинетикалық теорияның негізгі теңдеулерін жазған кезде молекулаларға сырттан ешқандай күш әсер етпейді. Сондықтан молекулалар ыдыс ішінде жылдамдықтары бойынша біртекті таралады деп жорығанбыз.

Бірақ кез-келген молекула жердің тартылу өрісінде орналасқандықтан оған ауырлық күші әсер етеді. Молекула әрдайым жылулық, хаосты қозғалыста болғандықтан, олар тартылу өрісінде белгілі биіктікке байланысты өзгеріп отырады. Жердің біртекті тартылу өрісінде молекуланың жылулық қозғалысы газ қысымы биіктікке байланысты кемитін, кейбір стационар күйіне әкеледі.

Молярлық массасы газдың теңіз деңгейіне салыстырғанда биіктіктегі қысымы қалыпты деп есептелінеді, ол мынаған тең:

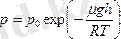
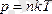
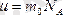
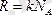қатынастарын пайдаланып, аламыз.

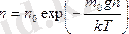
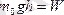
болғандықтан (тартылыс өрісіндегі молекуланың потенциалдық энергиясы) .

Сонымен 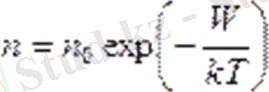мұндай таралу сыртқы потенциалдық өріс үшін Больцман таралуы (потенциалдық энергияның мәні бойынша бөлшектің таралуы) деп аталады.

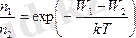
Осыдан тұрақты температурада газ молекуласының потенциалдық энергиясы аз жерінде тығыздығы үлкен екендігін көруге болады. Егер бөлшектердің массалары бірдей болып, бейтарап жылулық қозғалыс күйінде тұрса, онда тек ауырлық күші өрісінде ғана емес, кез келген сыртқы потенциалдық өріс үшін Больцман таралуы дұрыс.

Молекулалар жылдамдық бойынша таралуы

Газ молекулалары әр түрлі жылдамдықтармен қозғалыста болады да, әрбір жеке-жеке алынған молекула жылдамдығының шамасы да, бағыты да соқтығысулардың әсерінен ұздіксіз өзгеріп отырады.

Қозғалыстың барлық бағыттары теі ықтималды болғандықтан, молекулалардың бағыттар бойынша таралуы бір қалыпты болады: белгілі бір аралықта қалай болса, солай бағытталған, бірақ шамасы тұрақты $\mathbf{\mathrm{\Delta}Ώ}$ денелік бұрышта әрбір уақыт мерзімінде молекулалардың орташа есеппен $\mathbf{\mathrm{\Delta}N}$ болатын бірдей санының қозғалыс бағыттары жатады.

Молекулалардың жылдамдығының соқтығысуы кезінде өзгеруі кездейсоқ өтеді. Қайсыбір жеке молекула бірқатар жүйелі соқтығысқан сайын нәтижесінде оның энергиясы орташа мәнінен артып кетеді. Алайда газдың барлық молекулалары өз энергияларын жалғыз молекулаға беріп, өздері тоқталып қалады деп ойлағанның өзңнде бұл молекуланың энергиясы, демек оның жылдамдығы, шектеулі шамада болады. Сөйтіп, газ молекулаларының жылдамдығы қанай да бір v _мах -нан басталып ∞-пен бітетін мәндер қабылдай алмайды. Демек, жылдамдықтың орташа мәнімен салыстырғанда өте аз және өте үлкен жылдамдықтардың пайда болуының да ықтималдылығы өте аз болады, сонымен қатар v -нің осы мәнінің ықтималдылығы $\mathbf{v \rightarrow 0\ }$ кезінде де, $\mathbf{v \rightarrow \infty\ }$ кезінде де нольге ұмтылады.

Молекулалардың мәндері бойынша таралуын сандық сипаттап шығу тәсілін анықтау үшін төмендегідей әдісті пайдаланамыз. Жылдамдықтың мәндерін v осіндегі нүктелермен белгілейік. Сонда әрбір молекулаға осы осьтегі нүкте сәйкес келеді, санақ басы болып табылатын О нүктесінен осы нүктеге дейінгі қашықтық сан мәні жағынан қарастырылып отырған молекуланың жылдамдығының шамасына тең болады(1-сурет) .

1-сурет

Алынған нәтижені v осіндегі нүктелер түрінде кескіндей отырып, t уақыт мезеті үшін барлық молекулалардың лездік суретіна аламыз(2-сурет) .

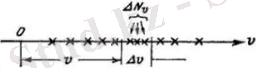
2-сурет

Жоғарыда көргеніміздей, жылдамдықтар негізінен ықтималдылығы анағұрлым көбірек мәнінің төңірегінде топтасады екен. Нольге жуық немесе өте үлкен мәнді жылдамдықтар өте сирек кездеседі. Сондықтан, v осінде нүктелердің орналасуы әркелкі, осьтің әртүрлі участкелерінде түрліше тығыздықпен таралыды.

Нүктелердің тығыздығын $\mathbf{\mathrm{\Delta}v}$ интервалына тап болатын $\mathbf{\mathrm{\Delta}N}$ нүктелер санының осы интервалдың

ρ=(∆N_v) /∆v (1)

Шамасына қатынасы ретінде анықтаймыз. Молекуланың арасындағы әрбір соқтығысу v осіндегі нүктелердің қалпын кездейсоқ түрде өзгертеді. Сондықтан t ₁ , t ₂ уақыт мезгілдері үшін суреттерді алып бір-бірімен салыстырамыз(3-сурет) .

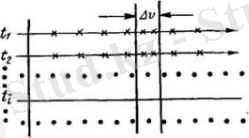
3-сурет

Әртүрлі пропорциялар үшін

f(v) =(ρ(v) ) /N=I/N (∆N_v) /∆v (2)

Қатынас бірдей болады. Осылайша анықталған $\mathbf{f}\left( \mathbf{v} \right)$ функциясы газ молекулаларының жылдамдықтар бойынша таралуын сипаттайды да таралу функциясы деп аталады. Берілген N молекулалардың ішінен жылдамдықтары $\mathbf{\mathrm{\Delta}v}$ интервалында жататын, яғни мәндері v-ден $\mathbf{v + \mathrm{\Delta}v}$ -ге дейінгі $\mathbf{\mathrm{\Delta}}\mathbf{N}_{\mathbf{v}}$ молекулалардың санын анықтаймыз:

$\mathbf{\mathrm{\Delta}}\mathbf{N}_{\mathbf{v}}\mathbf{=}\mathbf{Nf}\left( \mathbf{v} \right) \mathbf{+ \mathrm{\Delta}}\mathbf{v}\mathbf{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ (3)

Максвел таралу заңы

Таралу фунциясын теория жүзінде Максвелл ашты және соның есімімен аталады:

$\mathbf{f}\left( \mathbf{v} \right) \mathbf{= A}\mathbf{e}^{\mathbf{-}\frac{\mathbf{m}\mathbf{v}^{\mathbf{2}}}{\mathbf{2kT}}}\mathbf{v}^{\mathbf{2}}\mathbf{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ (4)

Мұндағы А - v -ге тәуелсіз көбейткіш, m - молекуланың массасы, k -Больцман тұрақтысы.

Молекулалардың жылдамдығын тұңғыш рет тәжірибеде 1920 жылы Штерн анықтады. Осы мақсатқа арналған прибор екі коаксиальді цилиндрден тұрады(4-сурет) .

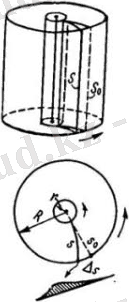
4-сурет

Прибордың осі бойынша күміс жалатылған платина жіп керілген. Жіпті электр тогымен қыздырған кезде оның бетімен күмістің атомдары буланып ұшып шығады. Ұшып шыққан атомдардың жылдамдықтары жіптің температурасына сәйкес келген. Жіпті тастап шыққан атомдар радиаль бағытарда қозғалады. Егер приборды айналмалы қозғалысқа келтіретін болсақ, онда жолекулалар шоғынының ізі сыртқы цилиндрдің бетіне қайсыбір шамаға ығысады (4-сурет) . Мұның себебі, күміс атомадары цилиндрдің арасындағы саңылаудан ұшып өткенше прибор $\mathbf{\mathrm{\Delta}\varphi}$ бұрышына бұрылып үлгереді, нәтижесінде атомдар шоғына қарсы сыртқы цилиндрдің екінші бір учаскесі тап келеді.

Бастапқы және ығысқан күміс жолақтарының ара қашықтығы $\mathbf{\mathrm{\Delta}S}$ цилиндр айналасының w бұрыштық жылдамдығымен, прибордың геометриясымен және атомдардың v жылдамдығын өрнектеуге болады. Ұшып өту уақытын $\mathbf{\mathrm{\Delta}t}$ арқылы белгілеп, былай жазуға болады:

$\mathbf{\mathrm{\Delta}s = \omega R\mathrm{\Delta}t\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ (5)

Мұндағы теңдеуден v жылдамықты табайық:

$\mathbf{v =}\frac{\mathbf{\omega}\mathbf{R}^{\mathbf{2}}}{\mathbf{\mathrm{\Delta}s}}$ (6)

Іздердің $\mathbf{\mathrm{\Delta}s}$ ығысуын және прибордың айналыс жылдамдығын өлшеп, атомдардың v жылдамдығын анықтауға болады. Жылдамдықтар бойынша таралудан томдардың қозғалысы күрделене түседі, олардың жылдамдықтары түрліше болып, ығысқан жолақ бұзылады. Іздің профилін зерттей отырып, күміс атомдарының жылдамдықтар бойынша таралуын шамамен есептеуге болады.

Штерн тәжірибесінің нәтижелері Максвелдің таралу заңынан шығатын атомдардың орташа жылдамдығының дұрыстығын дәлелдеді. Таралу заңы дәлірек Ламмерттің тәжірибесінде тексерілді. Таралудың сипаты жайлы бұл тәжірибе тек жуықталған мәліметтерді ғана бере алады.

Больцманның таралу заңы. Р қысымды nkT арқылы алмастырып, бірлік көлемдегі молекулалар санының биіктік бойынша өзгеру заңын анықтаймыз:

$\mathbf{n =}\mathbf{n}_{\mathbf{0}}\mathbf{e}^{\mathbf{-}\frac{\mathbf{\mu gh}}{\mathbf{RTT}}}$ (7)

Мұндағы $\mathbf{n}_{\mathbf{0}}$ - нольге тең болған биіктікте бірлік көлемдегі молекулалар саны, ал $\mathbf{\mu/R}$ қатынасын оған тең $\mathbf{m/k}$ қатынасымен алмастырып табылған өрнекті түрлендіруге болады:

$\mathbf{n =}\mathbf{n}_{\mathbf{0}}\mathbf{e}^{\mathbf{-}\frac{\mathbf{mgh}}{\mathbf{RTT}}}\mathbf{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ (8)

Бұл өрнегінен температура төмендегенде нольге тең емес биіктіктерде бөлшектер санының азаятындығы, ал Т=0 болғанда, нольге айналатындығы шығады(5-сурет) .

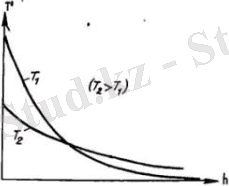
5-сурет

Сөйтіп, абсолют нольде барлық бөлшектер жер бетінде орналасқан болар еді. Молекулалардың биіктік бойынша әрбір нақты таралуы екі түрлі тенденцияның әсерлерінің нәтижесінде қалыптасады:

1. молекулалардың жерге тартылуы оларды жер бетінде орналастыруға тырысады

2. молекулалардың жылулық қозғалысы оларды барлық биіктіктер бойынша біркелкі таратуға тырысады. Неғұрлым m үлкен, ал Т аз болған сайын, бірінші тенденция күшейіп, молекулалар жер бетінде таяу жерде қоюлана түседі. Т=0 болатын шектік жағдайда жылулық қозғалыс толық тоқталып, молекулалар тартылыстың әсерінен жер бетінде орналасады. Жоғары температуралар кезінде жылулық қозғалыс артып, молекулалардың тығыздығы биіктеген сайын баяу түрде азая береді. Әр түрлі биіктікте молекуланың потенциалдық энергия қоры да әр түрлі болады:

$\mathbf{\varepsilon}_{\mathbf{p}}\mathbf{= mgh\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ (9)

Демек, молекулалардың биіктік бойынша таралуы сонымен қатар, олардың потенциалдық энергияларының мәндері бойынша да таралуы болып табылады. Жоғарыдағы өрнекті пайдаланып, төмендегідей формула жазуға болады:

$\mathbf{n =}\mathbf{n}_{\mathbf{0}}\mathbf{e}^{\mathbf{-}\frac{\mathbf{\varepsilon}_{\mathbf{p}}}{\mathbf{kT}}}\mathbf{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ (10)

Мұндағыы $\mathbf{n}_{\mathbf{0}}$ - молекуланың потенциалдық энергиясы нольге тең болатын жердегі бірлік көлемге келетін молекулалар саны, n - молекуланың потенциалдық энергиясы $\mathbf{\varepsilon}$ -ге тең болатын кеңістіктегі нүктелерге сәйкес келетін бірлік көлемдегі молекулалар саны.

Соңғы ормула бойынша, молекуланың потенциалдық энергиясының мәндері $\mathbf{\varepsilon}_{\mathbf{p1}}$ және $\mathbf{\varepsilon}_{\mathbf{p2}}$ болатын нүктелердегі n ₁ -дің n ₂ -ге қатынасы

$\frac{\mathbf{n}_{\mathbf{1}}}{\mathbf{n}_{\mathbf{2}}}\mathbf{=}\mathbf{e}^{\mathbf{-}\frac{\mathbf{\ }\mathbf{\varepsilon}_{\mathbf{p1}}\mathbf{-}\mathbf{\varepsilon}_{\mathbf{p2}}}{\mathbf{kT}}\mathbf{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }}$ (11)

Осыған сәйкес таралу Больцман таралу заңы деп аталады.

Сонымен қатар,

p = nkT, µ = m0NA, R = k NA

қатынастарын пайдаланып мына теңдіктерді аламыз : n = n0exp( - m0gh / kT )

m0gh = W - молекуланың тартылыс өрісіндегі потенциал

n = n0exp( - W / kT )

энергиясы, демек:

Бұндай таралу сыртқы потенциалдық

n1/n2=exp( -(W1 -W2) / kT)

өріс үшін Больцман таралуы деп аталады (бөлшектердің потенциалдық энергия мәндері бойынша таралуы) .

Бұдан мынадай қорытынды шығады: температура тұрақты болғанда қай жерде молекулалардың потенциалдық энергиясы аз болса, сол жерде газдың тығыздығы көп болады. Егер бөлшектердің массасы бірдей және олар хаостық жылулық қозғалыста болса, онда Больцман таралуы тек қана ауырлық күші өрісі үшін емес, кез-келген сыртқы потенциалдық өріс үшін де дұрыс болады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.