Евклидтік емес геометрияның шығу тарихы және Н.И. Лобачевскийдің өмірі мен ғылыми мұрасы


Қазақстан республикасының білім және ғылым министрлігі
М. Әуезов атындағы оңтүстік қазақстан мемлекеттік университеті
Реферат
Тақырыбы: Евклидтік емес геометрияның шығу тарихы
Орындаған:Аманқос Г. С
Жоспары:
1. Н. И. Лобачевский өмірі мен қызметі . . .
2. Н. И. Лобачевский геометриясының жарыққа шығуы . . .
Н. И. Лобачевский өмірі мен қызметі
Н. И. Лобачевский 1792 жылы 1 желтоқсанда бұрынғы Нижегород губерниясында туған. Гимназияны бітіргеннен кейін ол 1808 жылы Қазан университетіне оқуға түседі. Студент кезінде-ақ ол ғылыми жұмыстар жүргізді.
Н. И. Лобачевский 1810 жылы кандидат дәрежесін алады, ал 1811 жылы физика-математика ғылымдарынан өте жетік болуы себепті, ол кандидаттықтан магистрлікке көшіріледі. Магистрлік ғылыми дәреже оның "Аспан, денелерінің эллипстік қозғалыс теориясы" деген енбегі үшін берілді.
Магистр Лобачевский 1812 жылдан бастап педагогикалык жұмыска кіріседі. 1814 жылы профессор атағы берілгеннен кейін университеттің өзінде лекциялар оқиды. 1816 жылы Лобачевский Қазан университетінін профессоры болып бекітіледі. Ол университеттің белгілі ғалымы, көрнекті қоғам қайраткері болды.
1827 жылы Н. И. Лобачевский Қазан университетінің ректоры болып сайланады. Ол ректор болған жылдан бастап Қазан университетінің гүлдену дәуірі басталады.
Н. И. Лобачевский "Ғылыми жазбалар" журналында "Болжау геометриясы туралы" шет елдерде шығатын журналдарда (неміс тілінде) "Евклидтік емес" жаңа геометрия туралы оның бірнеше ғылыми мақалалары басылып шықты. Ол алгебрадан оқу құралын жазды.
Н. И. Лобачевскийдің ғылыми жұмыстары жайлы. Лобачевскийдің ғылыми еңбектері алгебра, геометрия, анализ, физика, механика және астрономия ғылымдарымен байланысты
20 жұмыстан тұрады. Лобачевскийдің “Алгебра және ақырлы есептеу” (Москва 1834), “Параллель түзулер теориясы бойынша геометриялық зерттеу” атты еңбектері бар.
Казань университетінің мүшелері 80 жылдар бойы Лобачевскийдің геометрияға қатысты шығармалар жинақтарын жинады.
1883-86 жылы Лобачевскийдің шығармаларында үлкен рөл атқарған шығармалар жинақтарының екі томы жарық көрді. Ол 400 данадан тұрған, соңғы жылдары библиографиялық сиректікті көрсетті.
Қазіргі кезде Лобачевскийдің шығармалары толық жинақ болып, алты томнан тұрады. Жоспар бойынша алғашқы үш томы Лобачевскийдің геометриялық шығармашылығынан тұрады, төртінші томында алгебра бойынша шығармашылықтары жинақталған, бесінші томы механика, астрономия анализ шығармашылықтарына қатысты болса, ал алтыншы томында Лобачевский туралы тарихи және библиографиялық мәліметтер жазылған.
Лобачевскийдің “Геометрия бастамалары” (1829-30) алғаш басылып шыққан мемуары геометрия тарихының екі кезеңінен тұратын шекарадан тұрады. Ол бірінші жағдайда 2000 жыл бойы математиктерге жұмбақ болып келе жатқан Евклидтің кез келген постулаты мен көрсетілген постулатты 100-ге жуық әртүрлі дәлелдеулер туралы сұраққа жауап іздесе, екінші жағдайда Лобачевскийдің мемуары геометрияның жаңадан бір бөлімін ашты.
Лобачевский осы мемуарда зерттеу мақсаты жайлы анықтап айтқан.
“Ешқандай математика ғылымы қараңғы түсініктен тұруға мүмкін емес екеніне бәрі келіседі, сондықтан параллель түзулер теориясында жіберілгендегідей математикада мұндай қатаң кемшілікке жол берілмеуі тиіс”.
Бұл теорияның Евклидтің параллель түзулер туралы постулатына сүйенетіні Лобачевскийді қызықтыра түсті. Ол осы Евклид постулаттарынан бас тартуды дұрыс деп шешіп, ішкі қайшылықтарын қорытындыламайтыннан өзгеше толығырақ өзінің геометриялық жүйесін құрды.
Лобачевский тамаша геометриялық салулар мен түсініктер көмегімен жаңа “жорамалдағы геометриядан” орын алатын жазық және сфералық геометрияға және аналитикалық геометрияға формула шығарды. Лобачевскийді “жорамал геометриясының” қаншалықты физикалық кеңістіктегі геометриялық арақатынасты бейнелейтіні қызықтырды. “Жорамал геометриядағы” анализ және интегралдық есептеуді қолдану формулалары да Лобачевскийдің назарында болды. “Геометрия бастамалары” мемуарының үлкен бөлігін осы тақырыпқа арнады.
Бұл мемуарда көбірек тараған Лобачевскийдің геометриялық зерттеулеріндегі мынадай барлық сұрақтар талданған:
“Жорамал геометрия” (1835), “Кейбір интегралдарды шешуде жорамал геометрияны қолдану” (1836), “Параллельдің толық теориясындағы жаңа геометрия бастамалары” (1835-38), “Параллель түзулер туралы геометриялық зерттеулер” (1840), “Пангеометрия”.
Лобачевский геометриясы кеңістіктер геометриясының теріс тұрақты қисықтығы, ал кәдімгі евклидтік геометрия геометрия кеңістігінің нөлдік қисықтығы болады. Бұдан Лобачевский мен Евклид кеңістігінің арасында маңызды айырмашылық бар екені шығады. Айырмашылықтарын ары қарай жалғастырайық.
Лобачевский геометриясында “қисықтық радиусы” деп аталатын “абсалют өлшем бірлігі” бар. Лобачевский кеңістігіндегі фигуралар R қисық радиусымен салыстырғанда өлшемі ең кіші болатындай евклид заңдылығы кеңістігі заңдылығына үлкен дәлдікпен бағынады. Дербес жағдайда үшбұрыштың қабырғалары R-мен салыстырғанда кіші болса, онда мына қатынастың
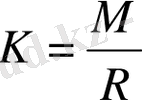 мағынасын, яғни кәдімгі стандарт ұзындық өлшемін абсалют ұзындық өлшеміне бөлінетіндігін айтып береді. Сондықтан, жеңіл өлшенетін үшбұрыш қандай да бір шектеулі санға тең қабырғаға ие болады, онда К кіші болған сайын, екі түзуден өзгеше бұрыштардың қосындысы да кемиді, яғни жеңіл түрде берілген бөліктері нақты кеңістіктегі геометрияның евклидтік геометриядан айырмашылығы аз ғана болады.
мағынасын, яғни кәдімгі стандарт ұзындық өлшемін абсалют ұзындық өлшеміне бөлінетіндігін айтып береді. Сондықтан, жеңіл өлшенетін үшбұрыш қандай да бір шектеулі санға тең қабырғаға ие болады, онда К кіші болған сайын, екі түзуден өзгеше бұрыштардың қосындысы да кемиді, яғни жеңіл түрде берілген бөліктері нақты кеңістіктегі геометрияның евклидтік геометриядан айырмашылығы аз ғана болады.
Егер К=0 болса, реалды кеңістік евклидті геометрияға, ал К≠0 болса, Лобачевский геометриясына айналады.
Лобачевский тәжірибелік жолмен біздің кеңістікте кәдімгі немесе жорамалданған геометрияны қолдануға бола ма, жоқ па, соны тексерді. Ол осы мақсатқа жету үшін Жерге, Күнге және қозғалмайтын Сириус жұлдызына қатысты үшбұрыштың бұрыштарының төбелерінің қосындысын анықтады. Есептеулер ешқандай анықталған нәтижеге әкеле алмағандықтан, мынаны мойындады: “евклидтік жағдай әрқашан дәлелдеусіз қалса да, ақиқат ғана болатыны өте ықтимал”.
Лобачевскийдің әлемдік даңқын геометриядан жасаған еңбектері шығарды.
Анализ бойынша Лобачевскийдің мынадай статьялары бар:
“Тригонометриялық қатардың жойылуы жайында” (1834), “Шексіз қатардың жойылуына сену әдісі және өте үлкен сандар функцияларының мәндеріне жуықтау” (1835), “Шексіз қатардың жинақтылығы туралы” (1835-36), “ Кейбір анықталған интегралдар мәні” (1852-53) .
Лобачевский осы статьяларының алғашқысында функция ұғымына жалпы анықтама берген және үзіліссіз дифференциалданатын функцияларды ажырата білген, сонымен қатар осы ұғымдардың әрбіреуіне жеке-жеке тоқталып өткен.
Лобачевский статьясының негізгі мазмұнында Пуассон, Дирихле, Риман және Лебег анықтаған нәтижеге сәйкес келетін анализ ғылымы бойынша алынған тригонометриялық қатарлар теориясына қатысты маңызды нәтижеге жетті.
Лобачевский осы сияқты геометрия және аналитикалық жұмыстарындағы “Алгебра және ақырлы есептеуде” оқытушылардың жетекшілігіне арналған және университет оқырмандарына қажет оқу құралын дайындап шығарған.
Лобачевскийдің “Алгебра” оқулығы он жеті бөлімнен тұрады, оның он үшінде элементар алгебра курстары жайлы көбірек жазылған; ал қалған бөлімдерінде “Тригонометриялық функция туралы” (14-бөлім), “Функция өсімшесі жайында” (15-бөлім),
“Екі айнымалыдан тәуелді теңдеулер” (16, 17-бөлім) .
Лобачевский “Алгебраның” алғашқы 7 бөлімінде арифметикалық амалдар туралы негізгі сандар түсінігіне баяндама жасады.
Сандарға амалдар қолдана отырып, Лобачевский алдымен осы амалдарға қатысты қасиеттерді (жалғыздық, коммутативті) қарастырды және жаңа сандарға қолданылатын амалдар өз күшін алдыңғы сандарға да сол қалпы сақтайтынын дәлелдеген.
Лобачевскийдің “Алгебрасының ” қалған бөлімдеріне көңіл аударсақ, біз автордың тек сол уақытта белгілі болған алгебраға қатысты материалдарды ғана емес, өзінің меншікті нәтижелерін ұсынғанын көреміз. Оған Греффе әдісін заңсыз иемденген жоғары дәрежелі теңдеулерді шешу әдісін жатқызуға болады.
Осыдан Лобачевскийдің “Алгебра немесе ақырлы есептеу” еңбегі сол кездегі алгебра курстарынан өзінің мазмұнының толықтығымен, әрі байлығымен және арифметикалық амалдарды баяндау қатаңдығымен ерекшеленеді.
Еңбегінің бірінші бөлімінде аксиоматикалық әдісті құрастыруға алғашқы қадам жасай отырып, аксиоматикалық арифметикалық салу қолданылды; ал қалған бөлімдері түпнұсқа мен жаңартылған түрді құрайды. Сондықтан, Лобачевскийдің “Алгебра” еңбегінің жарыққа шығуы математика тарихында аса көрнекті орын алады.
Лобачевскийдің: “Екі қосмүшеден тұратын теңдеулер дәрежесін төмендету” атты алгебраға қатысты екінші жұмысы
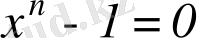 теңдеуінің шешімі
теңдеуінің шешімі
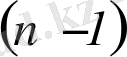 4 санына бөлінгенде ғана орындалады.
4 санына бөлінгенде ғана орындалады.
Лобачевскийдің геометриялық зерттеулерге қатысты жұмыстары ықтималдылықтар теориясымен тығыз байланысты.
Лобачевский евклидтік емес геометрия саласы бойынша параллельдер туралы аксиоманы зерттеді. Дедуктивтік түрдегі евклидтік геометрия жүйесі бірнеше аксиомалар жиынтығынан тұратыны бізге белгілі. Бұл аксиомалар арқылы мынадай әртүрлі түсініктер енгізілген: бірігу немесе жатады, рет, қозғалыс немесе конкуренттілік, үзіліссіздік немесе параллельдік.
Геометрияда параллельдіктің қолданылуының тәуелді немесе тәуелсіздігіне қатысты аксиомалар екі бөлікке бөлінеді. Бұл аксиомаға сүйенбейтін бөлігі абсалют геометрия деп аталады.
Бастапқы кезде Лобачевский осы айтылған аксиомаларды дәлелдеуге тырыса отырып, геометрияның абсалютті және абсалютті емес болып жіктелетініне көзі жетіп оны жүзеге асырды. Осының ізімен параллельдік аксиоманы теріске шығаруға әрекет жасады: берілген түзуде жататын нүкте арқылы осы түзумен жалғаспайтын кем дегенде бір түзу өтеді деп жорамалдады. Бұдан формальды қайшылықтың шықпайтынын байқады, ал ол қорыта келе евклидтіктен басқа геометрия бар екендігін шығарды.
Лобачевский “Геометрия негізінде қатаң дәлелденген параллельдер туралы теоремаға баяндама” атты шығармасы 1826 жылы 11(23) февральда болған Казань университетінің физика-математика ғылымы бөлімшесі мәжілісінде дүниеге келді.
1829 жылы Лобачевский осы еңбегін кең көлемді “Геометрия бастамалары” деген атпен шығарды.
Лобачевский геометриясының нақты бөлімі Евклид геометриясынан көп өзгешеленбейді. Негізгі бөлігінде параллельдің аксиомалары қолданылады.
Бұл бөлімі мынадай теоремалар жайында:
- Параллель түзулердің орналасуы;
- Көпбұрыштар мен үшбұрыштардың бұрыштарының қосындысы;
- Ауданы;
- Іштей сызылған шеңбер мен сырттай сызылған көпбұрыш;
- Тригонометрия;
- Пифагор теоремасы;
- Дөңгелектің өлшемі және оның бөліктері.
Бұл пунктте Лобачевскийдің екі өлшемді геометриясы евклидтік планиметриядан өзгешеленеді.
Лобачевский геометриясының кейбір нақты ерекшеліктерін қарастырып өтейік.
Түзуде жатқан нүкте арқылы осы түзумен беттеспейтін бірнеше түзу жүргізуге болады және ол шексіз көп. Олар шоқ жасайды. Бұл түзулер шоғында екі шеткі түзу болады, олар параллель түзулер деп аталады.
Бұл параллельдердің бағытын қарастырайық: түзулер параллель болса, бағыттары жақындай түседі, ал керісінше жағдайда алыстатылады.
Параллельдердің α бұрышы парллельдердің арақашықтығына тәуелді, яғни ұзындығы
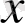 -ке тең перпендикуляр сәйкес келсе, мына түрде болады:
-ке тең перпендикуляр сәйкес келсе, мына түрде болады:
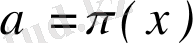 ,
,
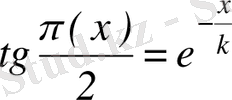
мұндағы
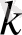 -таңдап алынған бірлік ұзындық тұрақтысы.
-таңдап алынған бірлік ұзындық тұрақтысы.
Егер х→с, онда
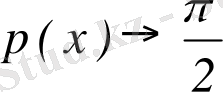 , осы сияқты х→∞, онда
, осы сияқты х→∞, онда
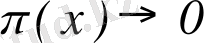
Осыдан перпендикуляр болып келетін түзулердің екі жаққа тарайтыны көрінеді.
Осыған ұқсас үшбұрыштың бұрыштарының қосындысы
 -дан кіші екені шығады. Көпбұрыштың қабырғалары көбейген сайын, бұрыштарының өлшемі азаяды. Барлық үшбұрыш аудандары
-дан кіші екені шығады. Көпбұрыштың қабырғалары көбейген сайын, бұрыштарының өлшемі азаяды. Барлық үшбұрыш аудандары

 түріндегі жоғары жақтарының жиынымен өрнектеледі, мұндағы:
түріндегі жоғары жақтарының жиынымен өрнектеледі, мұндағы:
 -аудан өлшеміне қатысты тұрақты.
-аудан өлшеміне қатысты тұрақты.
Лобачаевский геометриясында ұқсас үшбұрыштар мен көпбұрыштар қарастырылмайды.
Лобачаевский геометриясының ары қарай дамуы түзулер шоғының кіріспесімен тығыз байланысты. Олар: жинақты, жинақсыз және параллель.
Шоқта жататын түзулер циклдерден (с сызығынан немесе негізгі сызықтардан) тұрады.
Бұлар - түзулер шоғының ортогональ траекториясынан тұратын нүктелердің геометриялық орны. Ол шоғырдағы түзулердің біреуінде жататын бастапқы нүктемен анықталады. Бұл циклдер шоқтың үш түріне байланысты былай бөлінеді: шеңбер, эквидистанта (гиперцикл) және орицикл (
 шеңбердің бейнесі) .
шеңбердің бейнесі) .
Лобачевский геометриясындағы есептеу аппараттары гиперболалық функцияға негізделген.
Мысалы, Лобачевский геометриясындағы үшбұрышқа қатысты синустар теоремасы мына түрде болады:
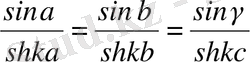
Барлық тригонометрия гиперболалық функцияның негізгі тригонометриясы болып шықты. Тригонометрияның көмегімен Лобачевский өзінің аналитикалық және дифференциалдық геометриясын жасады.
Н. И. Лобачевский геометриясының жарыққа шығуы
Евклидтік емес геометрия. Лобачевский идеяларын тану және интерпретация құру. Аксиомалық әдісті қалыптастыру.
Лобачевский өлді, бірақ оның геометриясы әлі танылған жоқ. Мыңдаған жылдар бойы құрылған салтты бұзған оның геометриялық идеялары қажетсіз болып көрінді. Ал егер кейбір геометрлер оның идеяларына аянышпен қараса да, олар Гаусс сияқты, ашық түрде өз пікірлерін айтуға бата алмады. Тек келесі онжылдықта Лобачевский идеялары қолдау тауып, одан әрі дамыды. Оның зерттеулерінің дұрыстығы анықталып, оның геометриясының қарама-қайшылығы болмау үшін математикалық ғылымдардың әрі қарай дамуы қажет болды. Оның идеялары, Лобачевский өлімінен кейін, тек 12-15 жылдан кейін ғана танылса, оның идеяларының математиканың әрі дамуына маңызды мәні бар тек ХІХ ғасырдың аяғында ғана анықталды.
Бұл танылымды әржақтағы келесі ғалымдар зерттеулері негізгі рөл атқарды. Дертн университетінде жұмыс істеген Ф. Миндинг неміс математигінің, Е. Бельтрам итальян математигінің, А. Кэли ағылшынның, Ф. Клейн неміс математигінің және А. Пуанкаре французының Лобачевскийдің еңбектерінің мәнін көрсету және оның идеяларын тарату бойынша Қазан Университеті және А. В. Васильевтың басқаруымен Қазан физика-математикалық қоғамы үлкен жұмыс жасады. Оның идеяларының кең танылуы 1893 жылы Қазан Университеті мен қоғам атап өткен ұлы ғалымның туғанына 100-жыл толуына тойында алынды. Сол кезде қоғам Лобачевский атындағы Халықаралық сый құрды. Келесі жылдары ірі геометрлер осы конкурстың лауреаттары болды: С. Ли, В. Киллинг, Д. Гильберт, Ф. Шур, Б. Вейнь, Э. Картан; совет ғалымдарынан В. В. Вагнер. 1896 жылы Университет алдында Н. И. Лобачевскийға ескерткіш қойылды.
Ұлы Отан соғысынан кейін 1950 жылы СССР ғылым Академиясы Н. И. Лобачевский атындағы жаңа сыйлық құрды. Келесі жылдары ол А. Д. Александровқа, Н. В. Ефимовқа, А. В. Погореловқа, А. С. Понтрагенға, Г. Хопфқа және П. С. Александровқа берілді.
1883 және 1886 жылдар Лобачевский еңбектерінің екі томы басылып шықты. Бірақ оның ғылыми зерттеулерінің толық жинағы тек Ұлы октябрь социалистік революциядан кейін басылды. Басылым бес томдық, 1946-1951 жылдары шықты. Түзетулер жасауға Москва және Қазан ғалымдарының үлкен тобы қатысты. Жаңа қорытындылар жасалғанда, келешекте қандай да бір қарама-қайшылықтар пайда болмайды ма деген күдік пайда болды. Бұл барлық теория, соңында өзін-өзі жойып жіберетін, бос қиял емес пе?
Бұл күдіктерді жоятын фактілер беттер теориясымен дайындалды, басында оны Эйлер және Лагранж талдады, одан кейін Монж және оның оқушылары. Гаусс еңбектерінде (1827) бұл теория жаңа бағыт алды. Гаусс беттің иілу кезінде, яғни оның формасын өзгертсе, бірақ қысу және созусыз, сақталатын беттегі фигуралар қасиеттерін зерттеген “беттің ішкі геометриясын” қарастыра бастады. Беттің ішкі геометриясына алдымен, келесі ұғымдар және шамалар жатады: “тегіс сызық”, “сызық ұзындығы”, “қиылысқан сызықтар арасындағы бұрыш”, “беттегі контурмен шектелген фигура ауданы”.
Сызық иілу кезінде ұзындығын сақтағандықтан, онда геодезиялық сызық деп аталатын, яғни азғана облыс үшін қысқа сызықтар беттің ішкі геометриясына жатады. Сферада мысалы, үлкен шеңберлер, жазықтықта-түзулер геодезилық сызықтар болып табылады. Қисық бетте геодезиялық сызықтар түзу қасиеттеріне жақын қасиеттерге ие. Әсіресе, олар өз бағытынан аз да болса да ауытқымайды, яғни олар бағыттарында қисық емес, жанама жазықтыққа параллель. Беттің ішкі геометриясын сипаттайтын формулалармен танысайық. Жазықтықта тік бұрышты декарт координат жүйесінде
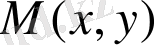 және
және
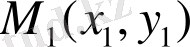 екі нүкте арасындағы арақашықтық квадраты мына формуламен өрнектелетіні бізге белгілі.
екі нүкте арасындағы арақашықтық квадраты мына формуламен өрнектелетіні бізге белгілі.
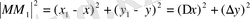
мұндағы
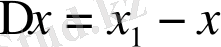 және
және
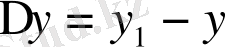 егер бұл нүктелер шексіз жақын болса, яғни
егер бұл нүктелер шексіз жақын болса, яғни
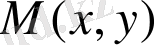 және
және
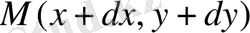 координаттары болса, онда олардың арасындағы
координаттары болса, онда олардың арасындағы
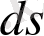 шексіз аз арақашықтығының квадраты
шексіз аз арақашықтығының квадраты
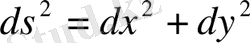
Кеңістікте нүктелер үш координатпен берілген
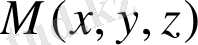 және
және
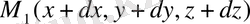 және
және
 .
.
Одан әрі біз бетке тиісті нүктелерді қарастырамыз. Бетті нүктелерінің үш координаттарын байланыстыратын біртеңдеумен беруге болады. Мысалы, центрі координат бас нүктесіндегі сфералы радиусы
 -ға тең қашықтықта орналасқан нүктелер жиыны ретінде анықтауға болады. Сонымен, сфераға тиісті нүктелер координатасы
-ға тең қашықтықта орналасқан нүктелер жиыны ретінде анықтауға болады. Сонымен, сфераға тиісті нүктелер координатасы
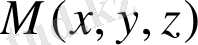 ,
,
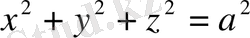 теңдеуін қанағаттандырады. Бірақ, кеңістіктегі бетті басқа да оның екі өлшемділігін көрсететін және жүйелі түрде Гаусс қолданған тәсілмен беруге болады. Бұл бетті параметрлік елестету деп аталады. Мұның мәні мынада: беттің
теңдеуін қанағаттандырады. Бірақ, кеңістіктегі бетті басқа да оның екі өлшемділігін көрсететін және жүйелі түрде Гаусс қолданған тәсілмен беруге болады. Бұл бетті параметрлік елестету деп аталады. Мұның мәні мынада: беттің
 нүктесінің
нүктесінің
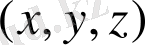 координаттарын
координаттарын
 және
және
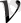 системалар функциясы ретінде өрнектейтін үш теңдеу жазу:
системалар функциясы ретінде өрнектейтін үш теңдеу жазу:

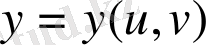
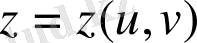
мұндағы
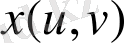 ,
,
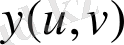 ,
,
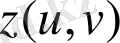 үздіксіз және дифференциалданатын функциялар. Белгілі шекараларда u және v-ны өзгерте отырып:
үздіксіз және дифференциалданатын функциялар. Белгілі шекараларда u және v-ны өзгерте отырып:
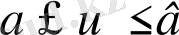
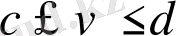
біз
 ,
,
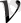 айнымалыларының берілген обылыстағы үздіксіз кеңістікте бейнеленуін аламыз, яғни беттің бөлігі.
айнымалыларының берілген обылыстағы үздіксіз кеңістікте бейнеленуін аламыз, яғни беттің бөлігі.
 және
және
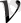 параметрлерін беттегі қисықсызықты координаталар деп аталады. Бұл мынамен түсіндіріледі: егер
параметрлерін беттегі қисықсызықты координаталар деп аталады. Бұл мынамен түсіндіріледі: егер
 -ды ғана өзгертсек (ал
-ды ғана өзгертсек (ал
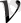 -ға тұрақты мән береміз
-ға тұрақты мән береміз
 ),
),
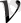 -сызық деп аталады, алынатын сызық мүлдем қисық болады.
-сызық деп аталады, алынатын сызық мүлдем қисық болады.
Енді егер
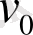 -мәнінің орнына басқа
-мәнінің орнына басқа
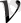 -мәндерін
-мәндерін
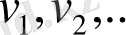 берсек, онда
берсек, онда
 -
сызық жиынын аламыз:
-
сызық жиынын аламыз:
 ,
,
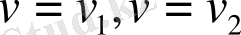 , … сонымен қатар
, … сонымен қатар
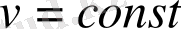 сызықтар жиыны деп те аталады. Осыған ұқсас екінші сызықтар жиыны анықталады:
сызықтар жиыны деп те аталады. Осыған ұқсас екінші сызықтар жиыны анықталады:
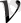 - сызықтар немесе, басқаша айтқанда
- сызықтар немесе, басқаша айтқанда
 сызықтары. Нәтижесінде бетте қисықсызықты тор пайда болады, және де әр нүкте арқылы
сызықтары. Нәтижесінде бетте қисықсызықты тор пайда болады, және де әр нүкте арқылы
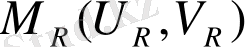
 -сызықтарының біреуі және бір
-сызықтарының біреуі және бір
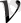 -сызық өтеді, және де олар жанаспайды, және
-сызық өтеді, және де олар жанаспайды, және
 -сызық пен
-сызық пен
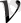 -сызықтардан құралған кез-келген бір ғана қиылысу нүктесіне ие болады. Сондықтан бұл торды қисықсызықтық координаттық тор деп атайды, ал сәйкес параметрлер мәндерін
-сызықтардан құралған кез-келген бір ғана қиылысу нүктесіне ие болады. Сондықтан бұл торды қисықсызықтық координаттық тор деп атайды, ал сәйкес параметрлер мәндерін
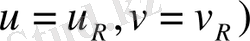 -
-
 нүктесінің қисықсызықтық координаттар. Мысал қарастырайық.
нүктесінің қисықсызықтық координаттар. Мысал қарастырайық.
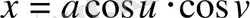
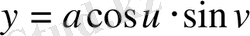
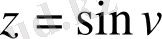 болсын
болсын
мұндағы
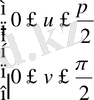
Бұл теңдеулер бірінші координаттар бұрышында жатқан центрі координаттар бас нүктесіндегі, радиусы
 сфераның бөлігін елестететін бет бөлігін анықтайды. Шынында да,
сфераның бөлігін елестететін бет бөлігін анықтайды. Шынында да,
 және
және
 параметрлері радиусы
параметрлері радиусы
 сферадағы географиялық координаталар болып табылатынын анықтауға болады:
сферадағы географиялық координаталар болып табылатынын анықтауға болады:
 -ені,
-ені,
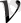 -бойлық. Өз еркімізше алынған М нүктесінен
-бойлық. Өз еркімізше алынған М нүктесінен
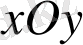 жазықтығына
жазықтығына
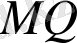 перпендикуляр жүргізейік,
перпендикуляр жүргізейік,
 нүктесінен-
нүктесінен-
 осіне
осіне
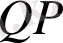 перпендикулярлығын
перпендикулярлығын
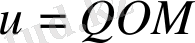 және
және
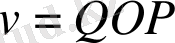 деп белгілеп, мынаны аламыз:
деп белгілеп, мынаны аламыз:
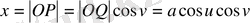 ,
,
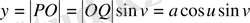 , егер
, егер
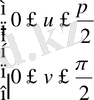 (*)
(*)
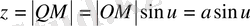 ,
,
Сонымен, біз сфераның көрсетілген бөлігінің нүктелері үшін алғашқы параметрлік теңдеулерін алдық. Осы теңдеумен анықталған барлық нүктелер координаталар бас нүктесіне
 қашықтықта орналасқанына тікелей көз жеткізуге болады. Шынында да, егер
қашықтықта орналасқанына тікелей көз жеткізуге болады. Шынында да, егер
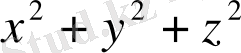 есептеп және
есептеп және
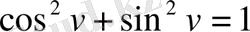 және
және
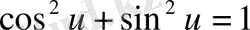 тепе-теңдіктерін қолдансақ, мынаны аламыз:
тепе-теңдіктерін қолдансақ, мынаны аламыз:
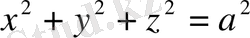
Берілген жағдайдағы қисықсызықтық координаттық тор ол сферадағы параллельдер мен меридиандар торы. Солтүстік полюс ролін атқаратын
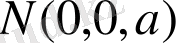 нүктеде тор дұрыстығы бұзылады, өйткені бұл нүкте арқылы бір емес, бірнеше меридиандардың шексіз жиыны өтеді (яғни бұл нүкте бойлығы анықталмаған) . Қалған нүктелерде тор дұрыс, яғни өзара бір мәнді сәйкестік бар:
нүктеде тор дұрыстығы бұзылады, өйткені бұл нүкте арқылы бір емес, бірнеше меридиандардың шексіз жиыны өтеді (яғни бұл нүкте бойлығы анықталмаған) . Қалған нүктелерде тор дұрыс, яғни өзара бір мәнді сәйкестік бар:
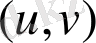 мәндерімен М нүктесі анықталады, және әр
мәндерімен М нүктесі анықталады, және әр
 нүктеде белгілі бір
v
бойлығы мен
нүктеде белгілі бір
v
бойлығы мен
 -
ені бар. Беттегі параметрлік теңдеулермен берілген
-
ені бар. Беттегі параметрлік теңдеулермен берілген
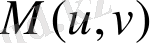 және
және
 нүктелерінің арасындағы қашықтық квадратының формуласын қарастырайық:
нүктелерінің арасындағы қашықтық квадратының формуласын қарастырайық:

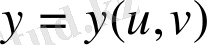

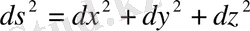 формуласын ескере отырып және
формуласын ескере отырып және
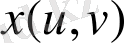 ,
,
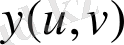 ,
,
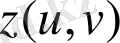 дифференциалдап,
дифференциалдап,
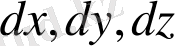 үшін
үшін
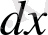 және
және
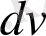 -ға қатысты сызықтық біртекті өрнектерді табайық. Оларды квадраттап қоссақ, ұқсас мүшелерін келтіргеннен кейін
-ға қатысты сызықтық біртекті өрнектерді табайық. Оларды квадраттап қоссақ, ұқсас мүшелерін келтіргеннен кейін
 қатысты екінші дәрежелі біртекті өрнек аламыз, яғни квадраттық форманы, оның коэффициенттері
қатысты екінші дәрежелі біртекті өрнек аламыз, яғни квадраттық форманы, оның коэффициенттері
 және
және
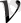 тәуелді функциялар (оларды әдетте
тәуелді функциялар (оларды әдетте
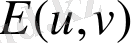 әрпімен белгілейді) .
әрпімен белгілейді) .
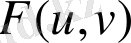 ,
,
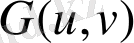 яғни
яғни
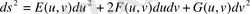 .
.
 үшін алынған өрнек беттің сызықтық элементі немесе бірінші дифференциалды квадраттық форма деп аталады. Иілуді сызықтық элемент, яғни шексіз аз ұзындық сақталатын беттің деформациясы ретінде анықтауға болады. Онда егер деформацияланған беттің сәйкес нүктелеріне сызықтық координаталардың
үшін алынған өрнек беттің сызықтық элементі немесе бірінші дифференциалды квадраттық форма деп аталады. Иілуді сызықтық элемент, яғни шексіз аз ұзындық сақталатын беттің деформациясы ретінде анықтауға болады. Онда егер деформацияланған беттің сәйкес нүктелеріне сызықтық координаталардың
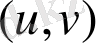 сол мәндерін көшірсек, онда деформацияланған беттің сәйкес нүктелерінде
сол мәндерін көшірсек, онда деформацияланған беттің сәйкес нүктелерінде
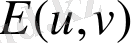 ,
,
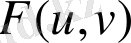 ,
,
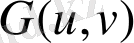 алғашқы мәндеріне ие болатындарын дәлелдеу оңай. Бірақ, дифференциалды геометрияда дәлелденгендей,
алғашқы мәндеріне ие болатындарын дәлелдеу оңай. Бірақ, дифференциалды геометрияда дәлелденгендей,
 және
және
 көмегімен доға ұзындығының, бұрыштың және фигуралар аудандарының шамасы өрнектеледі. Сонымен қатар геодезиялық сызықтардың дифференциалдық теңдеулері және біз иілудің алғашқы түсінігіне келеміз.
көмегімен доға ұзындығының, бұрыштың және фигуралар аудандарының шамасы өрнектеледі. Сонымен қатар геодезиялық сызықтардың дифференциалдық теңдеулері және біз иілудің алғашқы түсінігіне келеміз.
Гаусс ең жақсы (egreghium) деп атаған теоремасын дәлелдеді. Ол беттің
 берілген нүктедегі толық қисықтығы иілу кезінде өзгермейтінін, яғни иілудің инвариантты болып табылатынын дәлелдеді.
берілген нүктедегі толық қисықтығы иілу кезінде өзгермейтінін, яғни иілудің инвариантты болып табылатынын дәлелдеді.
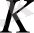 толық қисықтық деп
толық қисықтық деп
 бас қисықтар көбейтіндісін айтады, яғни беттің нормальдық қималарының қисықтығының экстремальдық мәндері. Бас қималар үнемі өзара перпендикуляр болады. Гаусс
бас қисықтар көбейтіндісін айтады, яғни беттің нормальдық қималарының қисықтығының экстремальдық мәндері. Бас қималар үнемі өзара перпендикуляр болады. Гаусс
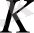 -ны тек
-ны тек
 арқылы өрнектейтін және олардың екінші ретке дейін
арқылы өрнектейтін және олардың екінші ретке дейін
 туындыларын беретін формуланы тапты, ал бұл иілу кезінде
туындыларын беретін формуланы тапты, ал бұл иілу кезінде
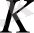 өз мәнін сақтайтынын дәлелдейді.
өз мәнін сақтайтынын дәлелдейді.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz