Ежелгі Мысыр математикасы

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

Қазақстан республикасының білім және ғылым министрлігі
М.Әуезов атындағы оңтүстік қазақстан мемлекеттік университеті

Реферат

Тақырыбы: Математика тарихының пәні
Орындаған:Аманқос Г.С

Жоспары:
Математика тарихының пәні.
Математиканың басқа ғылымдармен байланысы.

Математика тарихының пәні
Математика тарихын бірнеше кезендерге бөлуге болады:
Ежелгі Мысыр математикасы

Ежелгі Мысырдағы теңдеуді белгілейтін иероглифтар. Теңдеу: {\displaystyle ~x\left({\frac {2}{3}}+{\frac {1}{2}}+{\frac {1}{7}}+1\right)=37}
Ежелгі Мысыр әлемдегі ең байырғы мәдениет ошақтарының бірі. Ніл өзенінің екі жағалауына орналасқан бұл ел б.з.б. 3200-ші жж біртұтас мемлекет болып бірікті. Ніл өзені әр жылда тасып, жағалаудағы егістік жерлерді шайып кетіп отырған, тасу мезгілі аяқталған соң тұрғындардың жерін қайта өлшеп бөлу керек болады, ұзақ жылғы жер өлшеу тәжірибесінің арқасында геометрия ғылымы пайда болған (геометрия - грекше сөз, гео -- жер, метро -- өлшеу деген мағына береді).
Көне Мысырдың Ахмосе немесе Райнд папирусы
Б.з.б. 2900-шы жж кейін патшаларының мазары ретінде көне мысырлықтар көптеген алып пирамидаларды тұрғыза бастаған. Пирамидалардың құрылысына қарай отырып, сол кездегі көне мысырлықтардың геометрия мен астрономияны аз білмегенін аңғаруға болады. Мысалға, пирамида табаны мен бүйір бет ауданы арасындағы қатынас пен табанындағы бұрыштарды атауға болады.
Қазіргі кездегі Көне Мысыр математикасы туралы зерттеулер негізінен, сол кездегі монахтар жазуы және руни жазуымен жазып қалдырған екі кітапқа сүйенеді: бірі Лондонда (1858 жылы ағылшын жинаушысы Райнд тауып, өз меншігіне алған, сондықтан көбінесе Райнд папирусы деп аталады, ол папирус б.з.б. 1700 жылға жатады, бұл Мәскеу папирусына қарағанда үлкенірек). Енді бірі Москвада сақтаулы. Мәскеу папирусы деп аталады.
Оны 1893 жылы ескі заттарды жинақтап сақтаушы орыс әуесқойы Голенищев сатып алған, ал 1912 жылы ол Мәскеудегі әсемдік өнерлер мұражайына берілген. Папирус -- қамыс текті өсімдік. Мысырда, Ніл өзенінің жағалауында өседі. Оның өзегін тілімдеп алып, тілімдерді қатарластра орналастырады. Олардың үстіне көлденең осындай тілімдердің екінші қабатын салады. Қысқышпен екі қабатты біріктіріп жаныштағанда тілімдерден шығатын желім сияқты шырын қабаттарды тұтастырып қағаз түріне келтіреді.
Папирустар 9 ғ.-дан бастап мүлде қолданылмайтын болған, оның орнына қағаз пайдаланылады.
Қағаз ең алғаш бұдан 2000 жыл бұрын, Қытайда шыққан, оны Чай Лунь деген адам ойлап шығарған деп жазылады Қытай тарихнамаларында.
Қағаз жасауды қытайлардан Орталық Азия халықтары үйренген. 7 ғ. Самарқандта қағаз өндірісі болған. Осыдан арабтар үйренген, олар арқылы Еуропаға тараған.
Көне Мысырдың ертедегі әріптері сурет пішіндес әріптер болған, соңынан ретке келтіріліп демотикалық жазу пайда болған. Осы екі кітаптан басқа да кітаптар теріге, тастарға ойылып жазылған, олар қазір дүнйенің түкпір-түкпірінде сақтаулы. Екі кітаптың жазылған уақыттары шамамен б.з.б. 1850-1650 жж. сәйкес келеді.
Көне мысырлықтар ертеден ондық санау жүйесін қолдануды білген, бірақ оның әрбір орындағы сандардың жазылу ережесін білмеген, мысалға 111-ді жазу үшін, 1-ді үш рет қайталап жазбаған, керісінше әр орындағы 1-лерді әр түрлі белгілермен бейнелеген. Көне мысырлықтардың негізгі амалы қосу болған, ал көбейту қосудың қайталанып келуі ретінде есептелген. Олар бір айнымалысы бар бірінші дәрежелі теңдеулерді шеше алған, әрі арифметикалық, геометриялық прогрессиялардың қарапайым есептерін шеше алатын болған.
Сол кітапта (Мәскеу папирусы) және де шеңбердің ауданын есептеуді де көрсеткен: диаметрінің -ін алып тастағаннан кейін квадраттаған. Есептеу нәтижесінде PI=3. 1605 болып шыққан. Мәскеу папирусында жазылғаны бойынша олар дұрыс төрт жақтың көлемін есептеуді білген. Қорыта келгенде көне мысырлықтар көптеген нақтылы тәжірибелер топтаған, бірақ оны бір тұтас теорияға айналдырмаған.
Ежелгі Бабыл математикасы
Көне Мысырда математиканың туумен қатар ертедегі Бабыл тұрғындары және шумерлер мен аккадтықтар өз алдына өздерінің дербес математикасын жасап шығарды. Бұл халықтар сына сияқты сызықшалардан құралатын таңбалар арқылы (19 ғ-да археологиялық қазбалар кезінде табылған) күн көзіне қойғанда тастай қатайып қалатын, балшықтан жасалған саз балшықты тақталарға (плиткаларға) білімдерін жазып қалдырған. Мұндай балшық тақталар Бабыл жерінен мыңдап табылады.
Бабыл сандары

Бабыл сандары
Бабылдықтардың барлық математикалық жетістіктері жинақталып жазылған (шамамен айтқанда б.з.б. 200-шы ж., яғни Бабыл мәдениеті өркендеп өзінің ең жоғарғы сатысына көтерілген кезге жатады) қырық төрт кестеден құралған бабылдықтардың математикалық энциклопедиясы табылған. Бұл энциклопедиядан бабылдықтардың сол ертедегі заманда күнделікті мұқтаждықтары алға қойған практикалық есептерді: егіншілік, жер суаруды реттеу, сауда жасаудағы есептерді шешудің бірсыдырғы тиімді тәсілдерін білгендігі көрінеді.
Бабылдықтар астрономия ғылымының негізін салған. Бір аптаны жеті күнге бөлу, шеңберді 360 градусқа, сағатты 60 минутқа, минутты 60 секундқа, секундты 60 терцияға бөлу солардан бізге мирас болып қалған. Жұлдыздарға қарап болашақты болжау, яғни астрология да солардың арасында туған.
Бабылдықтар санаудың негізіне қазіргідей 10-дық жүйе емес, көп жағдайда арифметиканың аса қиын амалы -- бөлу амалын жеңілдететін 60-тық санау жүйесін қолданған. Мысалы: 1 574 640 санын алпыстық жүйеде өрнектесек: 1 603 + 57 602 + 46 60 + 40, яғни қосындысы 424000 етіп жазылады.
Әрбір өлшеуіш алдыңғысынан 60 есе артық болып келіп отыратын өлшеуіштер мен таразылар жүйесін де солар жасаған. Біздің қазіргі уақыт өлшемдеріміз -- сағатты, минутты және секундты 60 бөлікке бөлуміз содан басталады.
Бабылдықтар екінші дәрежелі теңдеулерді, ал арнаулы кестелер арқылы үшінші дәрежелі теңдеулерді шеше білген.
Ежелгі Урарту математикасы
Б.з.б. екінші мыңжылдықтың орта шенінен бастап бір жағынан Бабыл патшалығына, кейіннен оның орнына келген Ассирия патшалығына, екінші жағынан Кавказ сыртына шектескен территорияда Ван патшалығы немесе Урарту патшалығы болды, бұл патшалық 8 ғ-да Кавказ сыртының оңтүстік облыстарын жаулап алды.
Урарту халықтары Бабыл математикасын меңгеріп, қазіргі позициялық ондық (тұрған орнына қарай бір цифрдің өзі әр түрлі разрядтардың белгісі болатын) нумерацияға жақын және позициялық принципті білмейтін, мысырлық ондық нумерацияға мүлде ұқсамайтын, ондық нумерацияға көшкендігі анықталған.
Урарту арифметикасы көбінесе ертедегі Армян арифметикасына ұқсас. Бұлай болса ертедегі бабылдықтардың математикасы Урарту халықтары арқылы Кавказ сыртындағы халықтардың, әсіресе армяндардың өте ерте замандағы математикалық мәдениетіне ықпалын тигізіп математиканың ауқымды дамуына зор үлесін қосқан.
Араб математикасы
Орта ғасырдағы Орта Шығыс, Солтүстік Африка және Испания сынды мұсылман мемлекеттеріндегі араб жазуы арқылы жазылған математикалық шығармаларды айтады. Араб математикасының дамуына арабтар ғана емес, парсылар, сүриянилер, т.б. үлес қосты. Бұл шығармалар қолжазба түрінде осы күнге жеткен, олар әлемнің әр түкпіріндегі кітапханаларда сақтаулы тұр.
Араб математикасының дамуы орта ғасырдағы араб мәдениетінің дамуымен бірге дамыды. Оның дамуын үлкен жақтан үш кезеңге бөліп қарауға болады: 8 ғ. бастап 9 ғ-дың ортасына дейін әл-Мансұр халиф Бағдатта ішінде телескоп пен кітапханасы бар Даналық үйін (арабша: بيت الحكمة Bait al-Hikma) ашып, оған сол кездегі Сүрия, Үндістан т. б мемлекеттерден ғалымдарды жинайды, бұл кезең негізінен басқа тілдегі математикалық шығармаларды аударып, оны үйрету кезеңі деп айтуға болады. Ең алдымен Евклидтің Геометрияның бастамалары, одан кейін үнді математигі Брахмагупта еңбегі араб тіліне аударылады. Содан бастап Архимед, Аполлониус, Диофант, Птолемей сынды ертедегі гректің ұлы математиктерінің шығармалары іркес-тіркес араб тіліне аударылды. Бұл дәуірдегі атақты математик әл-Хорезми болды. Ол тек аудармамен айналысып қана қоймай, сонымен бірге Хорезми арифметикасы (көптеген кітаптарда Liber Algoritmi деп аталынып жұр), Әл-жәбр уә-л-Мұқабала т. б атты атақты кітаптары бар. Қазіргі кездегі математиканың маңызды бір саласы болып табылатын алгебраны осы әл-Хорезми енгізген.
IX-ғасырдың ортасынан XIII ғ-ға дейін араб математикасының гүлдену дәуірі деп қарауға болады. Осы кезеңде Бағдадта, Бұхара, Қаһира және Испанияның Кордова және Толедо қалаларында көптеген ғылыми зерттеу орталықтары пайда болды, бұл дәуірдегі атақты математиктерден Батани, Әбу-Уафа, Карачи, әл-Бируни, Омар Хайям, Насыреддин Туси, Банналарды атауға болады. XIV ғ-дан соң XV ғасырдағы Әмір Темірдің Самарқандтағы телескоп мен сонда зерттеумен айналысқан әл-Кашиды айтпағанда, бүкіл араб математикасының құлдыраған кезеңі болып табылады.
Араб математикасының негізгі жетістіктерінен, арифметика жағында: ондық санау жүйесі, жазбаша есеп (бұл екеуіне Үндістанның тигізген әсері бар), дәрежеге көтеру, біріз қатарлардың қосындысын табу формуласы, т. б. Ал алгебра жағында: бірінші және екінші дәрежелі теңдеулерді шешу, үшінші дәрежелі теңдеудің геометриялық шешу әдісі, екімүшеліктің жіктелуіндегі коэфициенттері т. б; геометрия жағынан: Евклидтің геометрияның алғашқы кітабының аудармасы, парралелдік туралы аксиоманың тереңдей зеріттелуі, PI санының мәні (әл-Каши 16-орынға дейін дұрыс есептеген) т. б; тригонометрия саласы да ертедегі грек пен үндіге қарағанда анағұрлым толық зерттелген.
12 ғ-дан бастап, араб математикасы Солтүстік Африкадағы Жерорта теңізі жағалау арқылы өтетін мәдени жолдары арқылы Испания мен Еуропаға тараған. Әсіресе ондық санау жүйесі мен жазбаша есеп, Евклидтің Геометрия бастамалары кітабының аударма нұсқасы т. б. бұлар бүкіл Еуропаның, тіпті дүние жүзінің математикасының дамуына орасан зор ықпал еткен.
Бірак, араб математикасының керемет туындылары латын тіліне аударылып Еуропаға тарамаған, тек 19-ғасырдан кейін араб математикасы реттеліп бір жүйеге келтіріле бастаған. Араб математикасы ертедегі гректің, Үндістанның, Қытайдың, Шығыс пен Батыстың математикалық жетістіктерін пайдаланып және оларды бір қалыпқа түсіріп Еуропаға таратқандықтан мәдениеттің қайта гүлденуі кезеңінде математика керемет дамыды, сондықтан да араб математикасы әлемдік
Математика ғылымының кіндігі де, тұсауыда кесілген жері ертедегі шығыс(Қытай, Үнді, Бабилон, Мысыр). Онан кейін, ол Бабилон мен Египет, Грекияға ауысады. Грекия математиктері математиканы өзінің нәтижелері мен түпкі қағидаларын логикалық қортынды арқылы келтіріп шығаратын дедукциялық ғылымға айналдырды. Гректер әсіресе бастапқы геометрияға жататын мәселелерді түгел зерттеді деуге болады.
Жаңа заманнан ілгері 47 ж. Рим әскерлері Грекияны басып алып Александрия портындағы Мысыр кемелерін өртегенде, өрт кітапхананы да шарпып, натижеде екі жарым ғасыр бойы жинап сақтаған кітаптар мен 500 мың парша қолжазба күйіп түгейді. 4 ғ. Христандар Грекия пұтханаларын өртеген кезде Серапис пұтханасындағы 300 қолжазба күйіп түгейді.
Міне осындай тарихи себептерден, әрі Грек математикасының өзіндегі олқылықтар себебінен, ежелгі Грекия математикасы тоқырайды. Осыған байланысты бүкіл Еуропада ғылым дамымақ түгіл, уақытысында болған ғылымдардың өздері жоғалып, Еуропаны қара түнек басады. Ақыл берген ғасырлардың орынына мың жарым жыл бойы үздіксіз созылған оянбайтын ұйқыға батқан Ақыл-ой ғасырлары келді. Адамзат тарихында мұнан үлкен, бұдан ғаламат ауыртпалық болған жоқ.
Шығыс математикасы 5 ғ-дан 15 ғ-ға дейінгі мың жылдан астам уақыт аралығында есептеудің әсіресе астрономияның қажетінен шұғыл дамыды, бұрынғы Грекия математиктерінің көпшілігі философ болса, кейінгі шығыс мәдениетінің көбінің астроном болуы міне осы себептен болса керек.
Матемактика тарихында, Гректердің мұрагерлері Үндістанлықтар делінеді. 200-жылдан 1200 жылға дейін Үндістан математикасы жоғары толқынға көтерілген дәуір есептеледі. Бұл дәуірдің бастапқы мезгілінде, олар Гректерден геометрияны Вавилоннан алгебраны ұйренді. Әрі Қытайдан үлгі алып арифметика мен алгебраны одан ары дамытты.
Үндістан математикасы

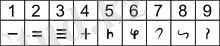
Үнді сандар (б.з. Iғ.)
Үндістан астрономиясы мен астрономиясын дәуір биігіне көтерген ғалымдар: Ариабхатия атты астрономиялық шығарманы авторы Ариабхатия (476-550) оның тригонометрияға қосқан үлесі төтенше зор.
Брахмагупта (598-?), ол отыз жасында Арифметикадан лекциялар және Анықталмаған теңдеулерден лекциялар қатарлы арнаулы тарауларды өзі ішіне алған, Брахма-сыбхута-ситханда (брахманың түзетілген жүйесі) атты әйгілі шығарма жазған. Ең алғаш теріс сандарға төрт амалды қолданған міне осы Брахма гупта.
Махавира (850-жылдар) Есептеу жауһары атты шығарнма жазған, кейбір тарихи деректерден қарағанда Қытайдың математикаылық кітаптаырынан пайдаланғандығы мәлім.
Үндіс математика тарихындағы ең биік тұлға Быхаскара Акария (1114-1185) Быхаскара астрономия, арифметика, өлшеу алгебраға қатысты көптееген шығармалардың авторы, солардың ішінді қызының атын қойған арифметика мен есептеуге жататын әйгілі шығармаысы Лайлауати (көрікті). Алгебралық шығармасы Вижаганита (түбірлерді есептеу) де теріс сандарды біршама кеңірек қарнастырған. Гректеер өлшемдес емес кесінділерді ең бұрын тапсадағы бірақ оның бір сан емес екенін мойындамады. Быхаскара басқа барлық Үндістан математиктерінен асқан кереметтігі иротционал сандарды сан деп қарап, иротционал сандар мен ратционал сандар арасындағы қатаң шекараны бұзып тастағандығы.
Сандардың ондық системасын Үндиялықтар алтыншы VІ ғасыырда игерді. ІХ ғасырға келгенде математик Махавира нөлді бір сан деп қарайды. Содан бастап ондық система одан ары кемелдене түседі. Қазіргі күнде бүкіл дүние жүзі қолданатын арғы түп төркіні Индыстан екендігі математика тарихынан азда болса хабары бар адамға белгілі болса керек.
773 жылы Үндыстаннан Бағдатқа көрнекті бір астроном келеді. Ол арабтарға одан 150 жыл бұрын жазылған Брахмабуттаның Брахма-сутта-сиддыханта атты кітабының санскирт тіліндегі нұсқасын береді. Бұл кіпты Мұхаммет Ибын Ибраһим әл-Фараби араб тіліне аударады. Араб астрономиясы міне осы кезден басталады. Хорезмидің редекциясымен ол екі рет шыққан. Сиддыхантха Хорезми көлемді теориялық кіріспе жазған. Хорезми өзінің Китап әл-джам уат тафрих би хисап әл-үнді атты кітабын үнеділердің үлгісімен жазады. Онда санау тіртібі, сандардың он сифыры арқылы жазылуы, аталуы, төрт амал, түбір шығару, жәй бөлшектерді есептеу айтылған. Бұл кітап 1150-жылы латын тіліне аударылған. Еуропалықтар Үнді сифырларын араб тіліндегі кітаптардың аудармаларынан көргендіктен араб сифыры деп атағаны мәлім.
Қытай математикасы

Ежелгі Қытайдағы қолданылған есептегіш құралдары
Тарих жылжып өтіп жатты, хандықтар ара бақталасы, хандық ішіндегі тах таласынан талай хандық ауысып, ғылым ордалары ойрандалып, адамзат ақыл ойының алыптары құғын-сүргін көрседағы ғылыми мұраларды халық көзінің қарашығындай сақтап өзигіліктеріне айналдырып отырды.
ХІІІ ғасырға келгенде шығыс Қытай, Батыс орта азия , таяу және орта шығыс елдері манғол билеушілернің қлдарына өтті. Осы елдер ара барыс-келіс, сауда мәдениет ауысу онан ары күшеюдің сыртында Юан патшалығы дәуірінде мұсылмандар ерекше мұрсатты жағдайларды болады, ордада әр қайсы өлке аймақтарда саяси, әскери, экономика және ғылым-техника орындарында негізгі басқару, манғолдардан қалса мұсылмандардың қолында болады. Мұсылман елдерінің көптеген астроном-математиктері хан ордасына келіп жылнама (календар) жасау қызметімен шұғылданды.
Юан патшалығы тарихындағы деректерден қарағанда Құбылайхан таққа шағар алдында (Құбылайдың хан болған кезі 1260-1294) жылдар аралығы) Жамалиддін бастаған бір топ мұсылман астрономадары сол кездегі манғол хандығының астанасы Шаңдуға (Ішкі манғолдың Долы ауданының шығыс оңтүстігі) шақырылады. Құбылайхан Жамалиддін қатарлы мұсылман астрономадарын қабылдап олардың білім-өнерін пайдалану туралы жарлық түсіреді . оларға ешқандай ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.