ГЕОМЕТРИЯ САБАҒЫНДА GEOGEBRA ОРТАСЫНЫҢ МҮМКІНДІКТЕРІН ҚОЛДАНУ ЖОЛДАРЫ

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 63 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі

«ГЕОМЕТРИЯ САБАҒЫНДА GEOGEBRA ОРТАСЫНЫҢ МҮМКІНДІКТЕРІН ҚОЛДАНУ ЖОЛДАРЫ»

2018 ж.

МАЗМҰНЫ

МАЗМҰНЫ: КІРІСПЕ . . .

: 3

: 1

МАЗМҰНЫ: GEOGEBRA - ДИНАМИКАЛЫҚ ОРТАСЫНЫҢ ГЕОМЕТРИЯ САБАҒЫНДАҒЫ ОРНЫ . . .

: 9

: 1. 1

МАЗМҰНЫ: GeoGebra туралы жалпы түсінік . . .

: 9

: 1. 2

МАЗМҰНЫ: GeoGebra ортасының жазықтықтағы мүмкіндіктері . . .

: 21

: 1. 3

МАЗМҰНЫ: GeoGebra ортасының кеңістіктегі мүмкіндіктері . . .

: 26

: 2

МАЗМҰНЫ: ГЕОМЕТРИЯ САБАҒЫНДА GEOGEBRA ОРТАСЫНЫҢ МҮМКІНДІКТЕРІН ҚОЛДАНУ ЖОЛДАРЫ . . .

: 31

: 2. 1

МАЗМҰНЫ: GeoGebra ортасының мүмкіндіктерін көрнекіліктер дайындауда қолдану . . .

: 31

: 2. 2

МАЗМҰНЫ: GeoGebra ортасында циркуль және сызғыштың көмегімен салу есептерін шешу мүмкіндіктері . . .

: 52

: 2. 3

МАЗМҰНЫ: Циркуль және сызғыштың көмегінсіз GeoGebra ортасында салу есептерін шешу мүмкіндіктері . . .

: 70

МАЗМҰНЫ: ҚОРЫТЫНДЫ . . .

: 79

МАЗМҰНЫ: ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . .

: 81

КІРІСПЕ

Білім - болашақ бағдары, сарқылмайтын қазына, мызғымайтын қорған, өмірлік азық. Білім - Отанымызды көркейтудің сан мың жолының ең тиімдісін таңдап алуға қызмет ететін ғажайып күш. Сонымен бірге ол үнемі қолдауды, жарнамалау мен насихатттауды қажет етеді. Болашақ ертеңі жастар, оларға сапалы білім беруге байланысты Елбасымыздың «Қазіргі заманда жастарға ақпараттық технологиямен байланысты әлемдік стандартқа сай мүдделі жаңа білім беру өте қажет» деген сөзі, қазіргі қоғамда ақпараттық технологияға білім беру жүйесінің терең бет бұруы болып отыр.

Оқытудың жаңа ақпараттық-коммуникациялық технологияларын меңгеру - қазіргі заман талабы. ХХІ ғасыр - ақпараттық технология ғасыры.

Ақпараттық құзіреттілікті қалыптастырудың басты мақсаты - оқушыларды ақпаратты беру, түрлендіру және оны қолдану білімдерімен қаруландыру, олардың компьютерлік технологияны өз қызметтерінен еркін, тиімді пайдалана алу қабілеттерін қалыптастыру.

Оқытудың ақпараттық-коммуникативтік және интерактивтік технологиялары бағыттары:

а) электронды оқулықтар;

ә) телекоммуникациялық технологиялар;

б) мультимедиалық және гипермәтіндік технологиялар;

в) қашықтықтан оқыту (басқару) Интернет.

Ақпараттық-коммуникативтік технологияны оқу-тәрбие үрдісіне енгізуде мұғалім алдына жаңа бағыттағы мақсаттар қойылады:

өз пәні бойынша оқу-әдістемелік электронды кешендер құру, әдістемелік пәндік Web - сайттар ашу;
жалпы компьютерлік желілерді пайдалану;
бағдарламалау ортасында инновациялық әдістерді пайдаланып, бағдарламалық сайттар, құралдар жасау (мультимедиалық және гипермәтіндік технологиялар) ;
қашықтықтан оқыту (Internet желісі) барысында өздігінен қосымша білім алуды қамтамасыз ету.

Соңғы жылдары заман ағымына сай күнделікті сабаққа компьютер, электрондық оқулық, интерактивті тақта қолдану жақсы нәтиже беруде. Білім беру жүйесі электрондық байланыс, ақпарат алмасу, интернет, электрондық пошта, телеконференция, On-line сабақтар арқылы іске асырылуда.

Бүгінгі күні инновациялық әдістер мен ақпараттық технологиялар қолдану арқылы оқушының ойлау қабілетін арттырып, ізденушілігін дамытып, қызығушылығын тудыру, белсенділігін арттыру ең негізгі мақсат болып айқындалады.

Елімізде білім беру саласында жаңа ақпараттық технологияларды қолдану басты мақсат болып отыр. Ол тек қана техникалық құрал емес, сонымен бірге жаңа ақпараттық коммуникациялық технология және білім беру жүйесіндегі сабақ берудің жаңаша әдісі болып табылады.

Қазіргі заман мұғалімі тек өз пәнінің терең білгірі болу емес, тарихи-танымдық, педагогиколық-психологиялық сауатты, саяси-экономикалық білімді және ақпараттық-комуникациялық технологияны жан-жақты меңгерген ақпараттық құзырлы маман болу керек. Әр оқытушы интерактивті тақтамен жұмыс жүргізуді толығымен меңгеруі қажет. Мен өз сабақтарымда интерактивті тақтаны пайдалану арқылы оқушылардың жаңа ойларын, әсерлі идеяларын тартымды етіп көрсететіндігін аңғардым. Жаңа материалдарды бірігіп талдауда маңызы зор болды.

Математика - ерекше құдіретті ғылым, ал математика пәнінің мұғалімі баланың бойындағы ақыл, білім, парасат, сабырлық, шығармашылық қасиеттерін бойын аша білетін тұлға. Қазіргі уақытта математика ғылымы кең етек алып дамуда. Сондықтан математиканы оқытудың мазмұнын ашуды жүзеге асыру үшін жаңа ақпараттық технология құралдары ауадай қажет. Қазіргі ақпараттық технологияның озық жетістіктерін математика сабағында қолдану арқылы танымдылық іс-әрекеттерін ұйымдастыра отырып, оқушылардың құзіреттілігін дамытуға болады.

Педагогикалық оқытуда ақпараттық технологияларды пайдаланудың бірнеше жолдары бар, солардың ішінде өз тәжірибемдегі қолданып жүрген әдіс-тәсілім мынадай: күнделікті дәстүрлі сабағымда; оқулық, көрнекілік құралдар, электрондық оқулықтартарды; компьютерлік құрылғыдан: презентация, дисктер, мультимедиа құралдарын, интернет-технологиясынан: интернет дербес ақпарат көзі ретінде, е-mail - ақпарат алмасу құралы ретінде, т. б. жиі пайдаланамын.

Қазіргі кезде тесттік әдістің көмегімен оқушылар білімі жиі сараланады. Тесттің саналылығы оның құру жүйесіне тәуелді және оған енетін тапсырмалардың күрделілігімен байланысты. Тест тәсілін қолдануды жүзеге асыру үшін жан-жақты ойластырып методикалық нұсқаулар, әдістемелер болуы қажет. Компьютер көмегімен тестік бақылау өткізуге болады. Компьютер бір мерзімде топтың, не сыныптың білімін тексеруге мүмкіндік береді. Ақпараттық технологиялардың оқу үрдісінде қолданылуы оқушылардың мүмкіндіктерін кеңейтеді. Ақпараттық технологияның міндеті-оқушыларды білімге қызығушылығын, ізденушілікке баулу. Заман талабына сай сабақта қолданылатын электрондық байланыс оқушылардың қызығушылығын арттырып, зейін қойып тыңдаумен қатар, түсінбей қалған сәттерін қайталап көруге, тыңдауға және алған мағлұматтарды нақтылауға мүмкіндік береді.

Компьютердің мультимедиалық мүмкіндіктерін, анимация мүмкіндігін, ілеспені, дыбыс меншіктеуді, гиперсылка көріністерін пайдаланып, осы көріністерді пайдалану әрекеттерін қолданып, тамаша, көрнекті, оқушыларды қызықтыра түсетін білім беру сабақтарын ұйымдастырған ыңғайлы. Электрондық оқулықпен оқытудың негізгі мақсаты - оқыту үрдісін үздіксіз және толық деңгейін бақылау, сонымен қатар ақпараттық-ізденіс қабілетін, шығармашылық қабілетін дамыту. Мұның тиімді жағы: электронды оқулықта әр сабаққа арналған бейне көрініс, анықтама сөздік, есептердің шығарылу жолы, фигуралардың кеңістікте орналасуы, диктант, тест тапсырмаларын, қайталау сұрақтарын пайдалана аламыз. Электронды оқулықты қолдану арқылы сабақта техникалық құралдарды, дидактикалық материалдарды қолдану тиімділігі, оқушының пәнге қызығушылығы, білім, білік, дағды деңгейін қалыптастыруы, білімнің тереңдігі, тексеру түрлері, бағалауы, практикалық дағдыларды игеруі артады. Оқушылардың өздері де алынған ақпаратты көшіріп алып, онымен өз ыңғайына қарай жұмыс істей алады. Мен өзімнің сабақтарымда оқытудың ұйымдастыру формаларының жеке, топтық, ұжымдық жұмыс жасау түрлерін пайдаланамын.

Математика сабағында компьютерді, мультимедиялық және электрондық оқулықтарды және интерактивті тақтамен презентацияны бірге қолданған сабақтарым өте нәтижелі өтуде.

Оқушылардың көпшілігінің естігенінің 5%-ын және көргенінің 20%-ын есте сақтайтыны белгілі. Аудио және видео ақпаратты бір мезгілде қолдану арқылы есте сақтауды 40-50%-ға арттыруға болады деп ойлаймын.

Ендігі сөзді, өзім сабағымның құрылымына ішінара енгізіп жүрген ГеоГебра бағдарламасы жайлы болмақ.

ГеоГебра - геометрия және алгебраны байланыстыратын компьютерлік интерактивті бағдарлама. Әлем бойынша ең көп таралған, 150-ден астам елде қолданылып отырған математикалық бағдарламаның бірі. Авторы - австриялық математик, PhD докторы Маркус Хохенвартер. Бағдарлама 50-ге жуық тілге аударылған және осы бағдарлама төңірегіндегі жұмысын 2001 жылы бастаған.

www. geogebra. org сайтынан ақпарат ала-аламыз, кез-келген компьютерге тегін орната беруге болады. Проекторы бар әр сыныпта математика сабағында пайдаланып, сабағыңды көрнекі етіп өтуіңе болады. Оқушылар абстрактілі түсініктерді өз көзімен «көре алады». Әрбір жаңа тақырыпты өту барысында осы бағдарламаны қолданған тиімді. Бұл оқушыларға ерекше қызық әрі түсінікті болады деп ойлаймын.

ГеоГебра арқылы:

«Жансыз» фигураларға, графиктерге жан бітіреді. Яғни, олар интерактивті болады.
Фигураларды анимациялауға болады.
Компьютерлік сауаттылықты арттырады.
Әзірге ГеоГебра қазақ тіліндегі жалғыз бағдарлама.

Байқау жұмысының өзектілігі : Бүгінгі таңда математиканы оқытуда ақпараттық-коммуникациялық технологияларды математиканың барлық саласында, сонымен қатар білім саласында да қарқынды енгізіліп отыр. Білімді тереңдету және оның практикалық маңызы жағынан тақырыпқа сай есептер шығаруда да осы технологияларды да қолданудың мәселесі көп жақты мәселе. Сондықтан да геометрия сабағында сандық білім беру ресурстарының бірі GeoGebra-ны пайдалану мәселелерін зерттеу өзекті болып табылады.

Ғылыми жаңашылдығы және практикалық маңыздылығы: егер, мұғалім математика сабағында оқытудың сандық білім беру ресурстарын қолдануға дағдыланса, онда ол оқушылардың білім сапасын көтеруге және ғылыми-ізденушілік, шығармашылық қабілеттерін арттыруға септеседі. Дипломдық жұмысты мектеп мұғалімдері және педагогикалық практика өтетін педагогикалық жоғары оқу орындарының студенттері қолдануларына болады.

Қарастырылған ғылыми мәселенің ағымдағы жағдайы: заман талабына сай математиканы оқытуда ақпараттық-коммуникациялық технологияларды қолдану қарқынды дамып келеді. Сонымен қатар математикалық сандық білім беру жүйелері де көптеп шығуда. Сол бағдарламаларды математика сабағында тиімді қолдана арқылы оқушылардың қызығушылықтарын арттырады, ал мұғалім өзінің кәсіби шеберлігін шыңдай алады.

Байқау жұмысының зерттеу обьектісі: математика сабағында оқытуда сандық білім беру ресурстарын пайдалану әдістері.

Байқау жұмысының мақсаты: геометрияны оқытуда GeoGebra ортасының мүмкіншіліктерін пайдалана отырып, оқушылардың ғылыми-ізденушілік және шығармашылық қабілеттерін дамыту.

Міндеттері:

математика сабағында оқушыларға сапалы білім беру үшін оқытудың ғылыми-зерттеу әдістерін қолдану мүмкіндіктерін анықтау.
сол ғылыми-зерттеу әдістерді практикада тиімді қолдана білу.

Байқау жұмысының зерттеу объектісі: орта мектепте математиканы оқыту үдерісі.

Байқау жұмысының теориялық және әдіснамалық негіздері: білім беру стандарты, математиканы оқытудың теориясы мен әдістемесі, мектеп геометрия курсының оқулықтары және әдістемелік нұсқаулықтары.

Байқау жұмысының құрылымы : кіріспе, екі тарау, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады.

1 GEOGEBRA - ДИНАМИКАЛЫҚ ОРТАСЫНЫҢ ГЕОМЕТРИЯ

САБАҒЫНДАҒЫ ОРНЫ

1. 1 Geogebra туралы жалпы түсінік

«Динамикалық математика» термині математикалық есептерді шешу үшін қолданылатын сызбаларға анимациялар беру арқылы математикалық зерттеулер жүргізуді айтамыз. Мұндай зерттеулерді GeoGebra, «Живая геометрия» және Maple кейбір пакеттері арқылы орындауға болады. Компьютерлік модельдеу динамикалық математиканың маңызды бөлігі болып табылады. «Динамикалық математика» терминінің баламалары «Динамикалық геометрия» және «Интерактивті геометриялық жүйе». Қазіргі таңда компьютер көмегімен шешілетін есептер түрі көбейді, яғни тек қана геометрия есептері емес, сонымен қоса алгебра және математикалық талдаудың кейбір есептерін де шығаруға болады.

Динамика анықтамасын мысал арқылы берейік, мектеп курсында шеңбер центр деп аталатын нүктеден бірдей қашықтықта жатқан нүктелер жиынтығын айтады. Динамикаға сәйкес шеңберді бір нүктеден қандай да бір қашықтықта жататын нүктені үздіксіз айналдыру арқылы сызамыз. Сол кезде біз осы сөздерге дәлел болатын тұйық сызық аламыз.

Динамикалық математика көмегімен көптеген математикалық ұғымдар мен теоремалар оқушыларға «көрінетін», «сезіне алатын», «түсінікті» болады. Сонымен қатар оқушы компьютерлік техниканы оқуда ғана емес, зерттеу есептерін шешу арқылы да үйренеді.

Математикалық есептерді динамикалық математикада есептеу үш этаптан тұрады:

Компьютер экранында есеп шартын геометриялық моделдеу;
Анимация мүмкіндігін қолдану арқылы есептің шешімін экранда көрсету;
Экрандағы көріністер бойынша есептің математикалық моделін құру [1] .

Динамикалық математикалық компьютерлік жарқын көріністерін GeoGebra ортасында салуға болады. GeoGebra - таралымы кең бола алатын динамикалық геометриялық орта, мұнда есептер мен математикалық ұғымдардың сызбаларын көрнекі де оңай түрде салуға болады. Сонымен қатар бұл бағдарламаның функциялармен орындалатын бай мүмкіндіктері бар. Атап айтатын болсам: функцияның графигін салу, түбірлерін есептеу, экстремумдарын табу, туынды мен интегралды есептеу және т. б. Бұл бағдарламаны Java тілінде Маркус Хохенвартер жасап шығарды. Java тілінде жасалған бағдарламалар көптеген операциялық жүйелерде жұмыс жасай алады. Кейін бұл бағдарлама 39 тілге аударылды. Geogebra - қызықты геометрияның толық нұсқасы мұғалімдерге тақырыпты түсіндіруге, ал оқушылар геометрия курсынан бөлек алгебра мен математикалық талдауда теңдесіз көмек беретін бағдарлама.

Мектепте геометрия мен алгебра пәндерін көбіне есеп-қисаппен түсіндіріп, оның айналамыздағы өмірмен байланыстыру жағы ақсап жатады. Бұл бағдарлама ғылымды меңгергісі келгендерге таптырмас құрал болып отыр [1] .

Біз бұл бағдарламада еш қиындықсыз нүктелерді, векторларды, сегменттерді, түзулерді және сонымен қатар өзгерісте болатын функцияларды сала аламыз. Бір жағынан түсініктеме-шкаласында тікелей жүргізуге мүмкіндік бар: g: 3x+4y =7 немесе: (x-2), 2+(y-3) 2=25 және бүкіл команда қатарын, дифференциялдау мен интеграциялауды қосқанда. GeoGebraның ең негізгі ерекшелігі - объектілердің екі жақтылығы: әрбір алгебра терезесіндегі түсінік геометрия терезесіндегі объектіге сәйкес келеді және керісінше.

Geogebra - тегін болғаннан кейін, оны кез-келген компьютерге орнатып, қолдануға болады. Проекторы бар әр сыныпта математиканы көрнекі түрде түсіндіру мүмкіндігі бар. Оқушылар абстрактілі түсініктерді өз көздерімен «көре алады». Әсіресе жаңа тақырыпты түсіндіру барысында бұл бағдарламаны қолданған тиімді. Әрі математикалық формулалармен шешілген есептерді көрнекі түрде графиктер салу арқылы тексеруге болады. Бұл әдіс оқушыларға ерекше қызық болып, формулаларды түсінікті түрде жеткізеді. GeoGebra арқылы «жансыз» фигуралар мен графиктерге жан бітеді. Яғни, олар интерактивті болады. Фигураларды анимациялауға болады. Компьютерлік сауаттылықты арттырады. Оның үстінде GeoGebra - тегін, әрі бірнеше тіліндегі математикалық жалғыз бағдарлама.

GeoGebra - тәуелсіз білім беретін, геометрия, алгебра және математикалық есептеулерді біріктіретін математикалық программа. Мұнда тек тышқанның көмегімен сіз нүктелерді, кесінділерді, векторларды, түзулерді және конустық қималарды, сонымен қатар басқа да функцияларды сыза аласыз және оларды өзгерте аласыз. Ол 2009-жылы бұл бағдарлама үшін арнайы байқаудың жеңімпазы атанды. 2011-жылдың тамызында оның үш өлшемді нұсқасы шықты.

GeoGebra - бұл тегін, оқытудың барлық деңгейіне сай, ыңғайлы әрі жинақы және кроссплатформалы динамикалық математикалық бағдарлама.

GeoGebra орта математиканы визуалдауға мүмкіндік береді, яғни математикалық есептерге зерттеулер мен тәжірибелер жүргізуге болады. Бұл бағдарламаның ерекшелігі циркуль мен сызғыштың көмегімен салынатын сызбаларды сызып, олардың геометриялық орнын ауыстыруға мүмкіндік береді. Сонымен қатар, геометриялық сызбаларды орын ауыстыру кезінде салынған параллельдік пен перпендикулярлық қатаң түрде сақталады [2] .

Мысалы, Х нүктесін параметрлерін жиынтығы бойынша құрал-саймандардың көмегімен 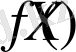функциясына тәуелді нүктенің анимациясын беріп, және бұл нүкте сызық бойында жылжу арқылы 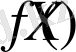функциясына тәуелді із қалдыру арқылы қандай да болмасын қисық сызықты сала алады. Бұл мүмкіндіктер арқылы функциялардың графиктерімен, әртүрлі екінші ретті қисықтарды (эллипс, гипербола, парабола, циклоида, кардиоида, Кассини сопақшасы, циссоида және т. б. ) салуға болады. Бұл циркуль және сызғыш арқылы сызылмайтын салу есептерін шығаруға жаңа көзқараспен қарауға мүмкіндік береді.

GeoGebra бағдарламасына әдістемелік жағынан қарайтын болсақ, оқылып жатқан оқу материалдарын әртүрлі деңгейде түсіндіріп, иллюстративті сызбадан, зерттеу сызбасына дейін деңгейін көтеруге болады. Тағы бір ерекшелігі ол сызбаларды салу үрдісі кезінде оқушылардың көптеген материалдарды меңгереді, математикалық білімі артады.

Сөйтіп, математиканы оқыту кезінде GeoGebra бағдарламасын қолдану қозғалыс енгізеді. Әрине, ескі әдістеме бойынша оқытуға болады, бірақ қазіргі жаңашыл ақпараттық технологияны меңгерген мұғалім болу заман талабы.

GeoGebra бағдарламасын құрал-саймандары бар шеберхана ретінде қарастырып, сызбаларың анимациясын дайындауға болады. Бұл бағдарламаны игеру үшін бағдарламалау тілін білу қажет емес [3] .

GeoGebra бағдарламасында жұмыс жасау үшін GeoGebra файлын ашу керек. Сол кезде 1. 1-суреттегідей терезе ашылады.

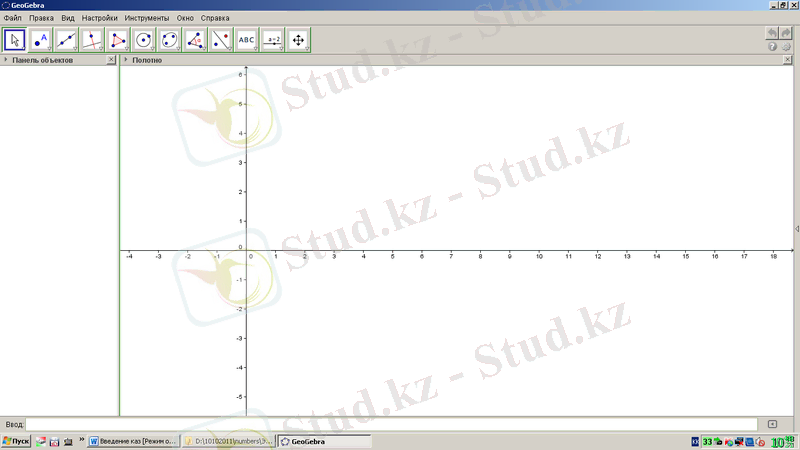
1. 1-сурет. GeoGebra бағдарламасының терезесі

GeoGebra алғашқы терезесі бірнеше қатардан тұрады.

Тақырып қатары
Мәзір қатары: Файл, Правка, Вид, Настройки, Инструменты, Окно, Справка

Файл мәзірі 1. 2-суреттегідей. Файлды құру, ашу, сақтау, баспаға шығару және шығу командалар тізімінен тұрады.

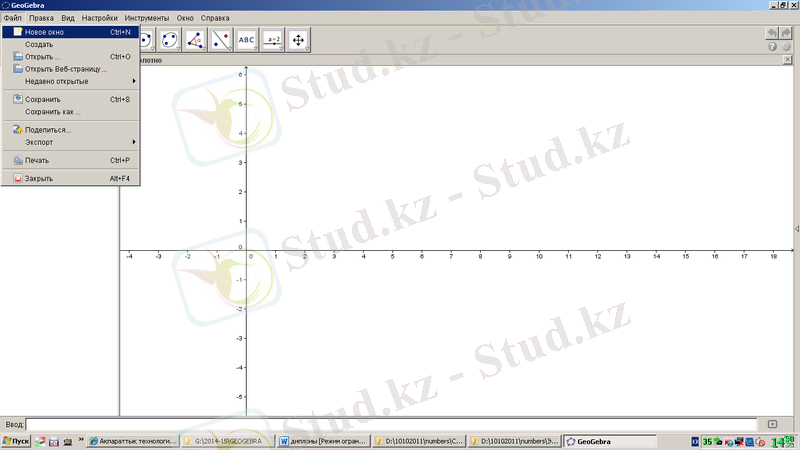
1. 2-сурет. GeoGebra бағдарламасының «Файл» мәзірі

Түзету (Правка) мәзірі 1. 3-суреттегідей. Жасалған операцияны болдырмай, қайта қалпына келтіру, көшіру, қою, буферге көшіру, суретті енгізу, қасиет және барлығын белгілеу командалар тізімінен тұрады.

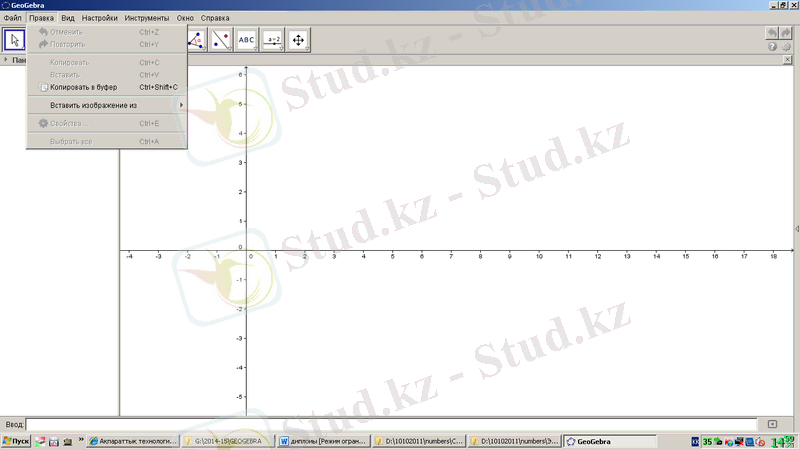
1. 3-сурет. GeoGebra бағдарламасының «Түзету» мәзірі

Түр (Вид) мәзірі 1. 4-суреттегідей. Объектілер панелі, кесте, CAS, Python, 3D жұмыс аймағы, жазықтықтағы жұмыс аймағы, екінші ретті жұмыс аймағы, хаттама, енгізу қатары, жаңалау, есептеу сияқты командалар тізімінен тұрады.

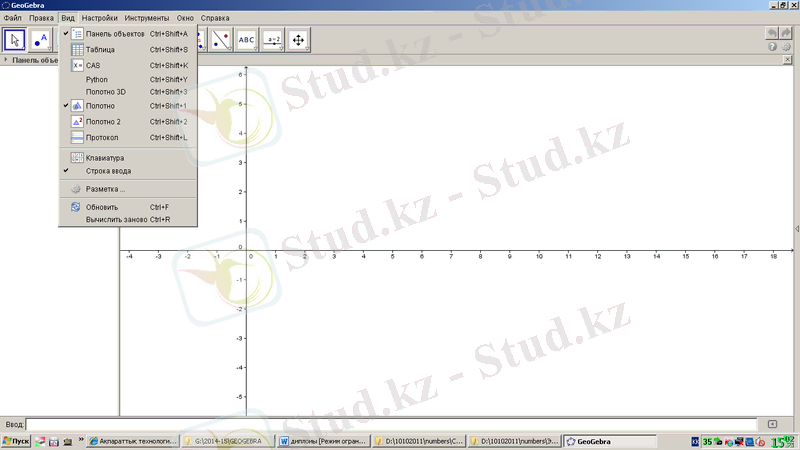
1. 4-сурет. GeoGebra бағдарламасының «Түр» мәзірі

Баптау (Настройки) мәзірі 1. 5-суреттегідей. Объектілердің бейнеленуі, нүктелерді бекіту, жуықтау, белгілеулер, шрифт өлшемі, тіл, қосымшалар, баптауларды сақтау, баптауларды алып тастау сияқты командалар тізімінен береді.

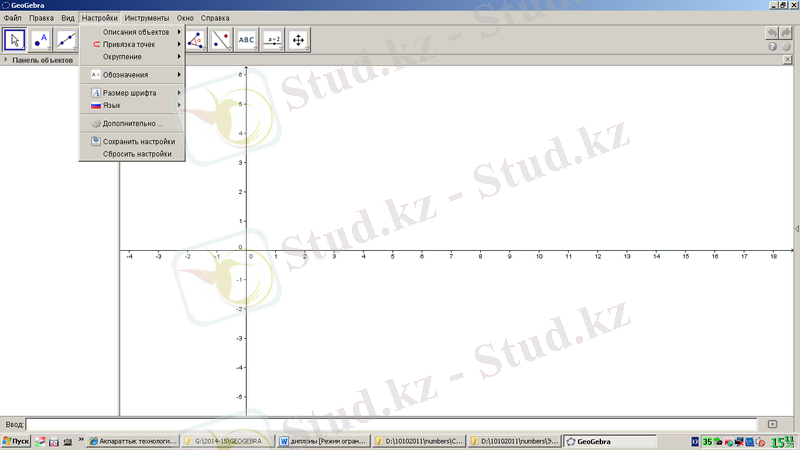
1. 5-сурет. GeoGebra бағдарламасының «Баптау» мәзірі

Құралдар (инструменты) мәзірі 1. 6-суреттегідей. Баптау, құрал құру, құралдарды басқару командалар тізімінен тұрады.

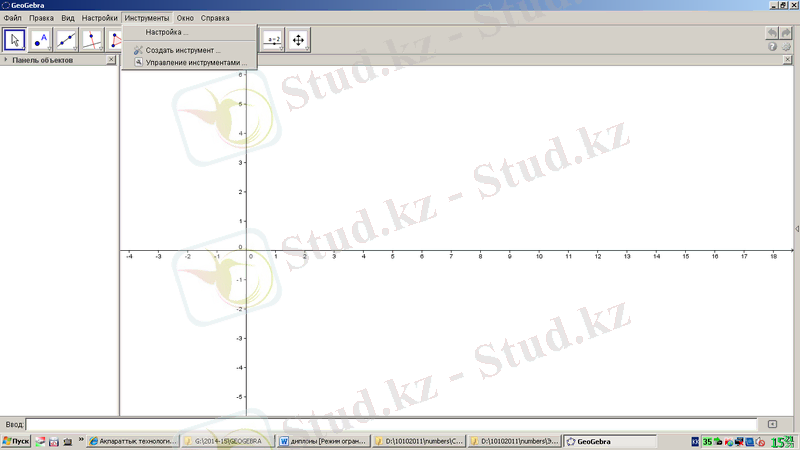
1. 6-сурет. GeoGebra бағдарламасының «Құралдар» мәзірі

Терезе (Окно) мәзірі 1. 7-суреттегідей. Жаңа терезе командасынан тұрады.

1. 7-сурет. GeoGebra бағдарламасының «Терезе» мәзірі

Анықтама (Справка) мәзірі 1. 8-суреттегідей. Анықтама, интернет арқылы көрсететін сабақтар, қателер туралы хабарлама, бағдарлама туралы ақпарат командалар тізімінен тұрады.

1. 8-сурет. GeoGebra бағдарламасының «Анықтама» мәзірі

Құрал саймандар қатары:

құралы тышқанның сілтемесі 1. 9-суреттегідей. Ол үш команданы орындайды: орын ауыстыру, нүктеге байланысты айналдыру, кестеге жазылым енгізу.

1. 9-сурет. GeoGebra бағдарламасының сілтеме құралы

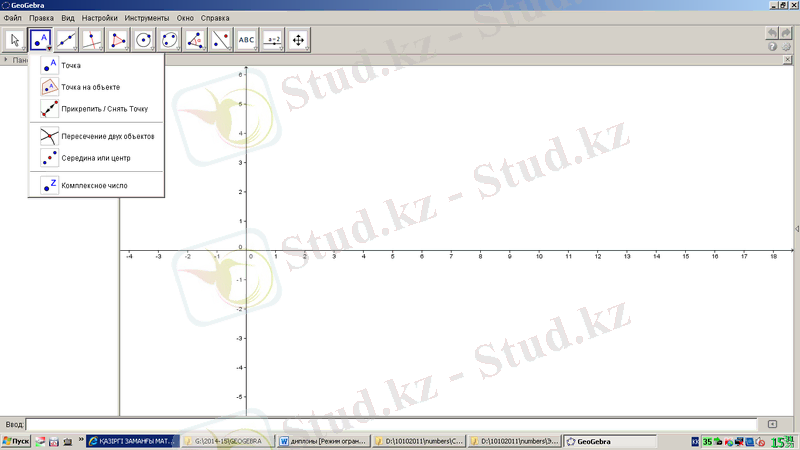нүкте құралы 1. 10-суреттегідей. Нүкте салу, объектіге нүкте салу, нүктені байлау және алып тастау, екі объектінің қиылысу нүктесі, орта немесе центр, комплекс сан командаларынан тұрады.

1. 10-сурет. GeoGebra бағдарламасының нүктеге қатысты құралдары

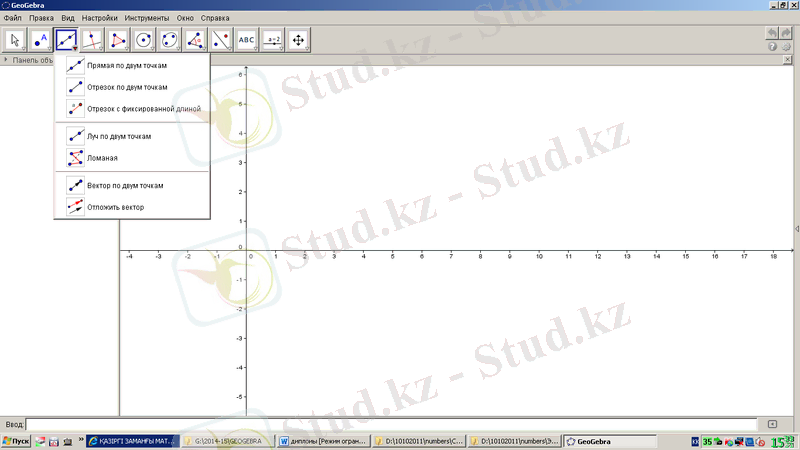кесінді құралы 1. 11-суреттегідей. Екі нүкте бойынша түзу сызу, екі нүкте бойынша кесінді сызу, белгілі өлшемі бойынша кесінді сызу, екі нүкте бойынша сәуле сызу, сынық сызық, екі нүкте бойынша вектор, векторды белгілеу командалар тізімінен тұрады.

1. 11-сурет. GeoGebra бағдарламасының кесіндіге қатысты құралдары

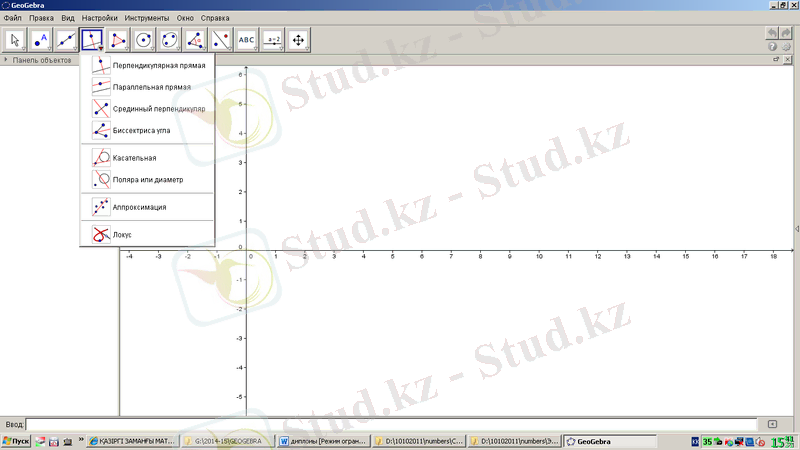әртүрлі объектілер салу құралы 1. 12-суреттегідей. Перпендикуляр түзу, параллель түзу, орта перпендикуляр, биссектриса, жанама, поляр немесе диаметр, апроксимация, локус командалар тізімінен тұрады.

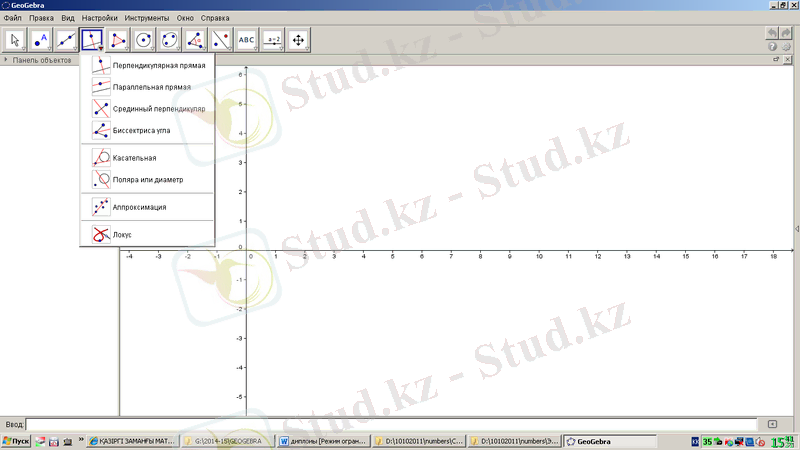
1. 12-сурет. GeoGebra бағдарламасының түзулерге қатысты құралдары

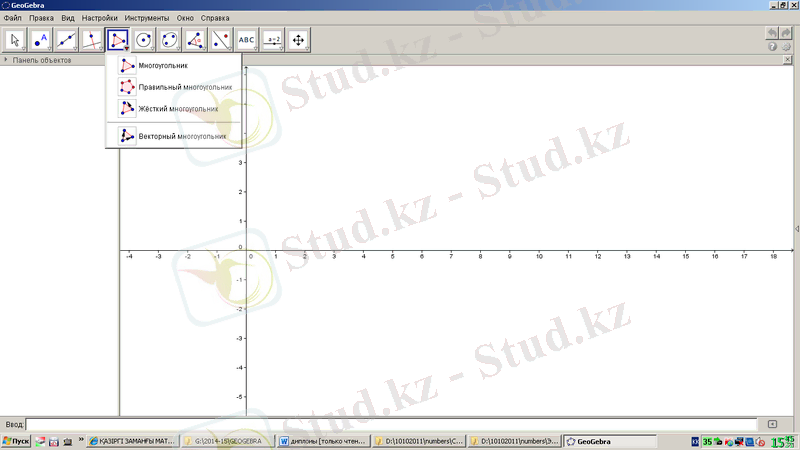көпбұрыш құралы 1. 13-суреттегідей көпбұрыш, дұрыс көпбұрыш, векторлы көпбұрыш, қатты көпбұрыш командалар тізімінен тұрады.

1. 13-сурет. GeoGebra бағдарламасының көпбұрышқа қатысты құралдары

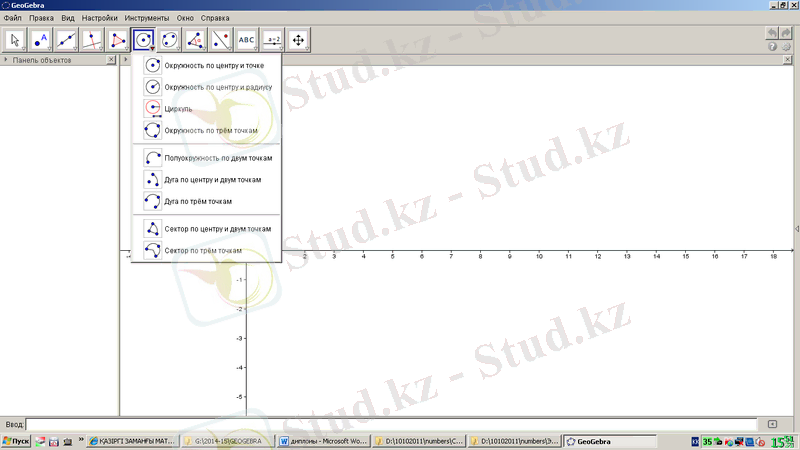шеңбер құралы 1. 14-суреттегідей. Центрі және нүктесі бойынша шеңбер, центр және радиусы бойынша шеңбер салу, циркуль, үш нүктесі бойынша шеңбер салу, екі нүкте бойынша жарты шеңбер, центр және екі нүктеден тұрады.

1. 14-сурет. GeoGebra бағдарламасының шеңберге қатысты құралдары

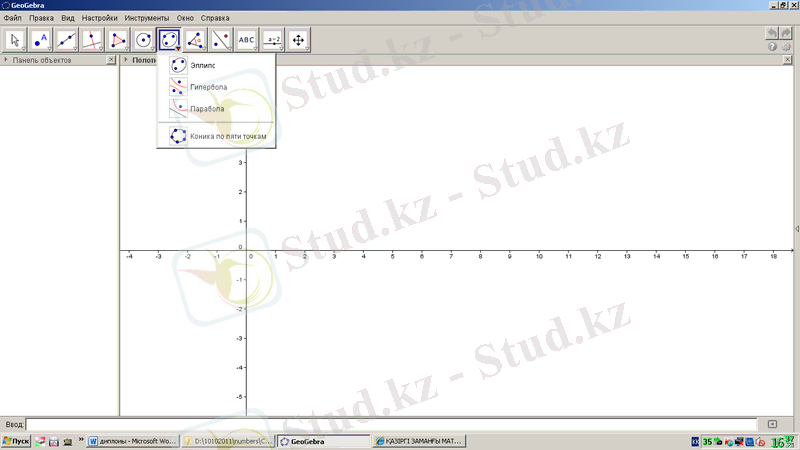екінші ретті қисықтар құралы 1. 15-суреттегідей. Эллипс, гипербола, парабола, бес нүктесі бойынша коника салу құралдарынан тұрады.

1. 15-сурет. GeoGebra бағдарламасының екінші ретті қисықтарға қатысты құралдары

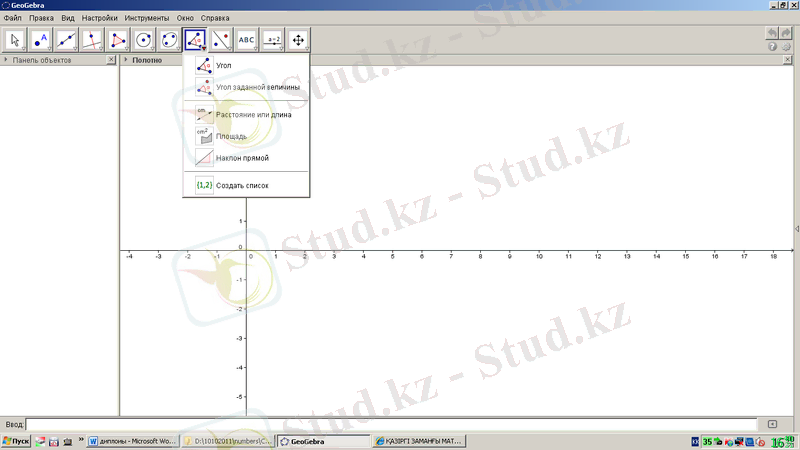өлшем құралы 1. 16-суреттегідей. Бұрыш, берілген өлшемі бойынша бұрыш, қашықтық және ұзындық, аудан, түзудің көлбеуі, тізім құру құралдарынан тұрады.

1. 16-сурет. GeoGebra бағдарламасының өлшемдерге қатысты құралдары

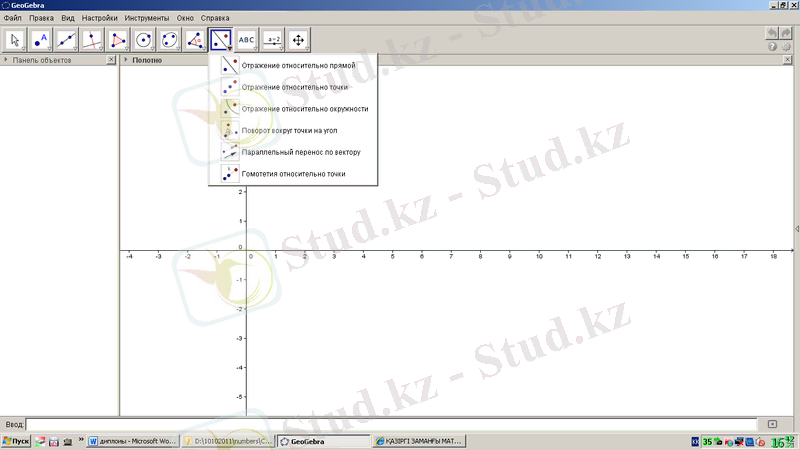түрлендіру құралы 1. 17-суреттегідей. Түзуге қатысты бейнесі, нүктеге қатысты бейнесі, шеңберге қатысты бейнесі, нүктенің бұрышқа бұрылуы, вектор бойынша параллель көшіру, нүктеге қатысты гомотетия құралдарынан тұрады.

1. 17-сурет. GeoGebra бағдарламасының түрлендірулерге қатысты құралдары

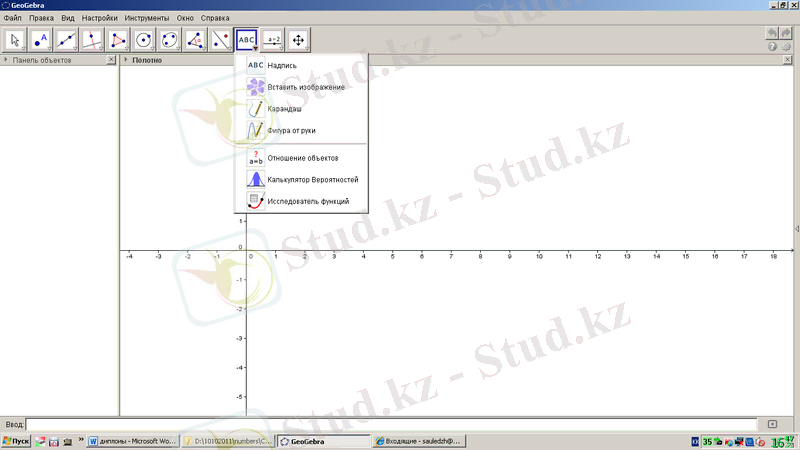енгізу құралы 1. 18-суреттегідей. Жазылым, сурет енгізу, қарындаш, қолдан фигура салу, объектілер қатынасы, ықтималдық калькуляторы, функцияны зерттеу құралдарынан тұрады.

1. 18-сурет. GeoGebra бағдарламасының әртүрлі обьектілерді енгізуге қатысты құралдары

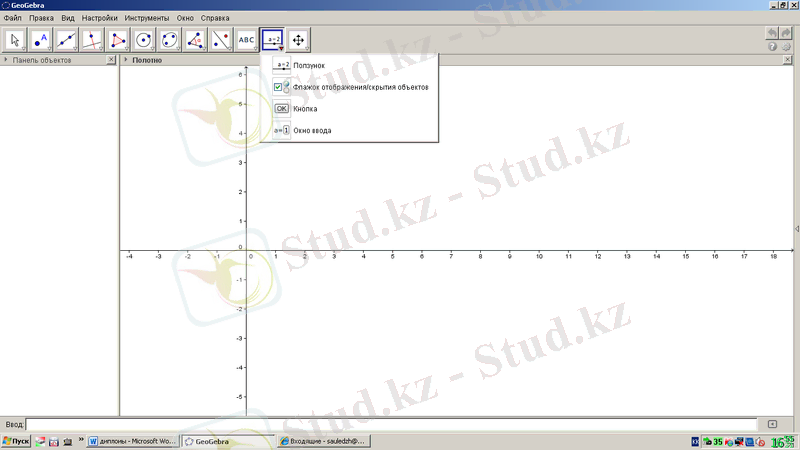батырмалар құралы 1. 19-суреттегідей. Ползунок, объектілерді бейнелейтін құрал, батырмалар, енгізу терезесі құралдарынан тұрады.

1. 19-сурет. GeoGebra бағдарламасының әртүрлі батырмалар енгізуге қатысты құралдары

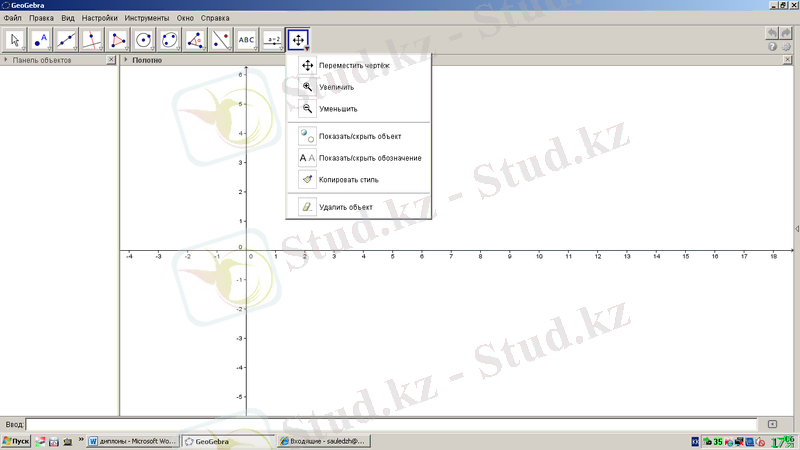түр өзгерту құралы 1. 20-суреттегідей. Сызбаны жылжыту, үлкейту, кішірейту, объектіні көрсету/жасыру, беліглеуді көрсету-жасыру, стильді көшіру, объекті өшіру құралдарынан тұрады.

1. 20-сурет. GeoGebra бағдарламасының сыртқы көріністерге қатысты құралдары

Жұмыс аймағы екі бөліктен тұрады. Cол жақ бөлігінде 1. 21-суреттегідей салынған сызбаның математикалық моделі, яғни формулалары жазылады. Ал оң жақ бөлігінде 1. 22-суреттегідей сызбаның өзі салынады.

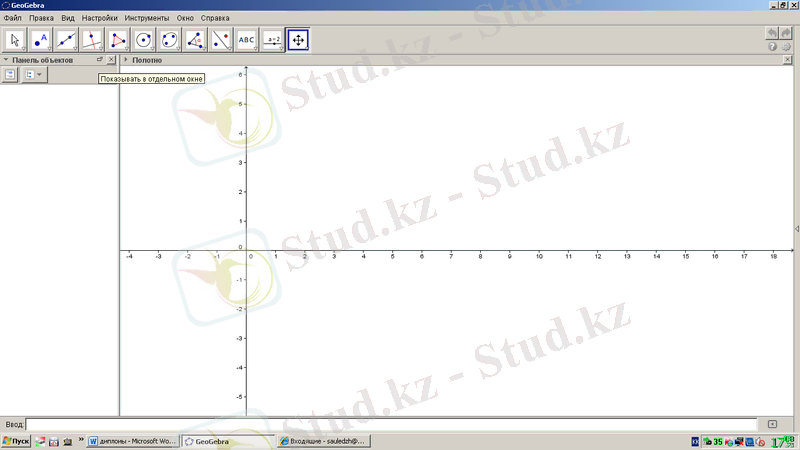
1. 21-сурет. GeoGebra бағдарламасының формулаларды енгізу аймағы

1. 22-сурет. GeoGebra бағдарламасының сызба салу аймағы

GeoGebra ортасының жазықтықтағы мүмкіндіктері

Geogebra бағдарламасын аты айтып тұрғандай, геометрия және алгебра сөздерінен құрылған, яғни геометрия және алгебра пәндері бойынша көмекші құрал деп санауға болады.

Енді GeoGebra-да жұмыс істеуге мысал келтірейін.

Мысал 1: Үшбұрышқа сырттай шеңбер салу.

Тапсырма: GeoGebraны пайдаланып, 1. 23-суреттегідей АВС үшбұрышына сырттай шеңбер салу керек.

АВС үшбұрышына сырттай шеңбер салу тәртібі:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.