Көпбұрыштар мен дөңес көпбұрыштар

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 68 бет
Таңдаулыға:

Қазақстан республикасының ғылым және білім министрлігі

ХАЛЫҚАРАЛЫҚ ГУМАНИТАРЛЫҚ ТЕХНИКАЛЫҚ УНИВЕРСИТЕТІ

Бердиева Гулназ Мардабаевна

Мектеп геометрия курсында көпбұрыштар мен көпжақтарды оқытудың әдістемесі

ДИПЛОМ ЖҰМЫСЫ

5В010900 - «Математика» мамандығы

Шымкент 2020 ж.

Қазақстан Республикасы білім және ғылым министрлігі

Халықаралық гуманитарлық техникалық университеті

«Техника және ақпараттандыру» кафедрасы

«Қорғауға жіберілді»

«Техника және ақпараттандыру»

кафедра меңгерушісі

т. ғ. к., Оспанова Р. Д.

«__» 2020 ж.

ДИПЛОМ ЖҰМЫСЫ

Тақырыбы: «Мектеп геометрия курсында көпбұрыштар мен көпжақтарды оқытудың әдістемесі»

5В010900 - «Математика» мамандығы бойынша

Орындаған

Бердиева Г. М.

Орындаған:

Бердиева Г. М.:

Орындаған:

Ғылыми жетекші

т. ғ. к., доцент, аға оқытушы

Бердиева Г. М.: Акылбаев М. И.

Шымкент 2020 ж.

Халықаралық гуманитарлық техникалық университеті

«Жаратылыстану-техникалық және спорт» факультеті

5В010900 - «Математика» мамандығы

«Техника және ақпараттандыру» кафедрасы

БЕКІТЕМІН

БЕКІТЕМІН: Кафедра меңгерушісі

БЕКІТЕМІН:

Дуйсенов Н. Ж.

: ^{(қолы/подпись)}

БЕКІТЕМІН:

^{(А. Ж. Т. /Ф. И. О. )}

БЕКІТЕМІН: «

2019ж. г.

Диплом жұмысын орындауға

ТАПСЫРМА

Студент Бердиева Гулназ Мардабаевна ___

4 - курс, МТ-16 тобы, 5В010900 - «Математика» _.

1. Диплом жұмысының тақырыбы Мектеп геометрия курсында көпбұрыштар мен көпжақтарды оқытудың әдістемесі .

«___» ___2019ж. № ректордың бұйрығымен бекітілген.

2. Аяқталған жұмысты тапсыру мерзімі «___» 2020 ж.

3. Жұмысқа бастапқы деректер

«Мамандық бойынша дипломдық жұмысты орындауға арналған әдістемелік нұсқама» және «Диплом жұмысы туралы ереже»

4. Диплом жұмысын дайындауға арналған сұрақтар тізімі

а) Евклидтік кеңістіктегі көпбұрыштар мен көпжақтар теориясы: Дөңес фигуралар. Көпбұрыштар мен дөңес көпбұрыштар; Көпбұрыш және оның характеристикасы; Тең шамалы және тең құрамды көпбұрыштар; Көпжақтар. Дөңес көпжақтар;

б) Дұрыс және топологиялық дұрыс көпжақтар: Топологиялық дұрыс көпжақтар; Дұрыс көпжақтар;

в) Мектеп геометрия курсында көпбұрыштар мен көпжақтарды оқыту әдістемесі: «Көпбұрыштар» тақырыбын оқытуда оның теориялық негізін қолдану ерекшеліктері; «Үшбұрыштар» тақырыбын оқыту ерекшеліктері; Мектеп геометрия курсындағы көпбұрыштардың ауданын оқыту әдістемесі; «Көпжақтар» тақырыбын оқытуда оның теориялық негізін ескеру ерекшеліктері.

5. Графикалық материалдар тізімі

6. Ұсынылатын негізгі әдебиеттер тізімі 1. Шыныбеков Ә. Н. Геометрия. Жалпы білім беретін мектептің 7, 8, 9 сыныптарына арналған оқулық. -Алматы: Атамұра, 2005.

2. Геометрия, 7-11: Учеб. для общеобразоват. учереждений// Л. С. Атанасян, Б. Ф. Бутузов, С. Б. Кадомцев и др. -М. :Просвещение, 2001, 206с.

3. Земляков Л. Н. Геометрия / учебное пособия для учителя. М. : Просвещение, 2002.

7. Жұмыс бойынша кеңес

Тараулар, бөлімдер атауы, №: Тараулар, бөлімдер атауы, №

Ғылыми жетекші, кеңесші: Ғылыми жетекші, кеңесші

Тапсырманы алған мерзімі: Тапсырманы алған мерзімі

Тапсырма берілді (қолы): Тапсырма берілді (қолы)

Тапсырма қабылданды (қолы): Тапсырма қабылданды (қолы)

Тараулар, бөлімдер атауы, №: Евклидтік кеңістіктегі көпбұрыштар мен көпжақтар теориясы

Ғылыми жетекші, кеңесші: Акылбаев М. И.

Тапсырманы алған мерзімі: 15. 01. 2020

Тапсырма берілді (қолы):

Тапсырма қабылданды (қолы):

Тараулар, бөлімдер атауы, №: Дұрыс және топологиялық дұрыс көпжақтар

Ғылыми жетекші, кеңесші: Акылбаев М. И.

Тапсырманы алған мерзімі: 20. 02. 2020

Тапсырма берілді (қолы):

Тапсырма қабылданды (қолы):

Тараулар, бөлімдер атауы, №: Мектеп геометрия курсында көпбұрыштар мен көпжақтарды оқыту әдістемесі

Ғылыми жетекші, кеңесші: Акылбаев М. И.

Тапсырманы алған мерзімі: 25. 03. 2020

Тапсырма берілді (қолы):

Тапсырма қабылданды (қолы):

8. Диплом жұмысын орындау кестесі

№

Жұмыс кезеңдері

Жұмыс кезеңдерінің орындалу мерзімі

Ескерту

№: 1

Жұмыс кезеңдері: Диплом жұмысының тақырыбын бекіту

Жұмыс кезеңдерінің орындалу мерзімі: 05. 01. 2020

Ескерту:

№: 2

Жұмыс кезеңдері: Диплом жұмысын дайындау үшін материалдар жинақтау

Жұмыс кезеңдерінің орындалу мерзімі: 15. 02. 2020

Ескерту:

№: 3

Жұмыс кезеңдері: Диплом жұмысының теориялық бөлімін дайындық(1тарау)

Жұмыс кезеңдерінің орындалу мерзімі: 20. 02. 2020

Ескерту:

№: 4

Жұмыс кезеңдері: Диплом жұмысының аналитикалық бөлімін дайындық (2-3 тарау)

Жұмыс кезеңдерінің орындалу мерзімі: 20. 03. 2020

Ескерту:

№: 5

Жұмыс кезеңдері: Диплом жұмысы мәтінінің қолжазба нұсқасын толық аяқталуы

Жұмыс кезеңдерінің орындалу мерзімі: 10. 04. 2020

Ескерту:

№: 6

Жұмыс кезеңдері: Диплом жұмысын алдын ала қорғауға ұсыну

Жұмыс кезеңдерінің орындалу мерзімі: 25. 04. 2020

Ескерту:

№: 7

Жұмыс кезеңдері: Диплом жұмысын сын пікірге ұсыну

Жұмыс кезеңдерінің орындалу мерзімі: 11. 05. 2020

Ескерту:

№: 8

Жұмыс кезеңдері: Диплом жұмысының аяқталған нұсқасын ғылыми жетекшінің пікірі және сын пікірімен ұсыну

Жұмыс кезеңдерінің орындалу мерзімі: 11. 05. 2020

Ескерту:

№: 9

Жұмыс кезеңдері: Диплом жұмысын қорғау

Жұмыс кезеңдерінің орындалу мерзімі: 15. 05. 2020

Ескерту:

Тапсырманың берілген күні «»2019 ж.

Ғылыми жетекшісі Акылбаев М. И., т. ғ. к., доцент, аға оқытушы

Тапсырманы қабылдаған студент Бердиева Г. М.

МАЗМҰНЫ

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: АНЫҚТАМАЛАР, БЕЛГІЛЕУЛЕР ЖӘНЕ ҚЫСҚАРТУЛАР . . .

6: 6

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: КІРІСПЕ . . .

6: 7

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 1 ЕВКЛИДТІК КЕҢІСТІКТЕГІ КӨПБҰРЫШТАР МЕН КӨПЖАҚТАР ТЕОРИЯСЫ . . .

6: 9

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 1. 1 Дөңес фигуралар. Көпбұрыштар мен дөңес көпбұрыштар……… . . .

6: 9

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 1. 1. 1 Фигура және дөңес фигура . . .

6: 9

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 1. 1. 2 Көпбұрыштар . . .

6: 12

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 1. 1. 3 Дөңес көпбұрыштар . . .

6: 13

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 1. 2 Көпбұрыш және оның характеристикасы . . .

6: 15

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 1. 3 Тең шамалы және тең құрамды көпбұрыштар . . . .

6: 17

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 1. 4 Көпжақтар. Дөңес көпжақтар . . .

6: 20

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 1. 4. 1 Көпжақтар . . .

6: 20

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 1. 4. 2 Дөңес көпжақтар . . .

6: 21

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 2 ДҰРЫС ЖӘНЕ ТОПОЛОГИЯЛЫҚ ДҰРЫС КӨПЖАҚТАР . . .

6: 25

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 2. 1 Топологиялық дұрыс көпжақтар . . .

6: 25

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 2. 2 Дұрыс көпжақтар . . .

6: 28

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 3 МЕКТЕП ГЕОМЕТРИЯ КУРСЫНДА КӨПБҰРЫШТАР МЕН КӨПЖАҚТАРДЫ ОҚЫТУ ӘДІСТЕМЕСІ … . . .

6: 33

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 3. 1 «Көпбұрыштар» тақырыбын оқытуда оның теориялық негізін қолдану ерекшеліктері . . .

6: 33

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 3. 2 «Үшбұрыштар» тақырыбын оқыту ерекшеліктері . . .

6: 39

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 3. 2. 1 Үшбұрыштардың теңдігін оқытуда «геометриялық теңдіктің» мәнін ашу жолдары . . . … . . .

6: 39

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 3. 2. 2 «Тең бүйірлі үшбұрыш» тақырыбын оқыту әдістемесі . . .

6: 46

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 3. 2. 3 «Үшбұрыштың бұрыштарының қосындысы» тақырыбын оқыту әдістемесі . . .

6: 47

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 3. 3 Мектеп геометрия курсындағы көпбұрыштардың ауданын оқыту әдістемесі . . . . . .

6: 51

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: 3. 4 «Көпжақтар» тақырыбын оқытуда оның теориялық негізін ескеру ерекшеліктері . . .

6: 64

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: ҚОРЫТЫНДЫ ……… . . . . . .

6: 71

НОРМАТИВТІК СІЛТЕМЕЛЕР . . .: ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . .

6: 73

НОРМАТИВТІК СІЛТЕМЕЛЕР

Бұл дипломдық жұмыста келесідей стандарттарға сілтемелер жасалған:

Білім жөніндегі құжаттарды рәсімдеу үлгілері: 2007 жылдың 21 қарашада №5651 Қазақстан Республикасының білім ғылым министірлігінің бекіткен бұйрығы.

Халықаралық гуманитарлық техникалық университетінің Әдістемелік Кеңесімен бекітілген, 2019ж., дипломдық жұмыс туралы ережелер .

5В010900 - «Математика» мамандығы бойынша күндізгі және сырттай түрде оқитын студенттерге дипломдық жұмысты орындауға арналған әдістемелік нұсқау. Халықаралық гуманитарлық техникалық университеті, 2019ж.

АНЫҚТАМАЛАР, БЕЛГІЛЕУЛЕР ЖӘНЕ ҚЫСҚАРТУЛАР

Планиметрия (лат. planum - жазықтық және METREO - "өлшеймін") - элементар геометрияның жазықтықта жатқан фигуралардың қасиеттерін зерттейтін бөлімі.

Функция - бір айнымалыға басқа бір айнымалының бір мәнің сәйкес қоятын тәуелділік, заң.

Арифметика (грек. arіthmētіkē, arіthmos - сан) - сандар (бүтін және бөлшек) және оларға қолданылатын амалдар туралы ғылым (грекше arіthmetіke, arіthmos - сан) .

Конфигурация - белгілі бір жүйені, аппараттық жабдықтарды, оның нақты параметрлерін (сипатгамаларын), құрылғылар қүрамын (бөліктерін), өзара байланыстарын анықтай отырып орналастыру.

Аксиома (көне грекше: ἀξίωμα - лайықты қабылданған қағида) - нанымдылығы ақиқат (шындық) болғандықтан логикалық дәлелдеусіз алынатын қағида; теорияның ақиқат (шындық) ең бастапқы қағидасы.

Палетка (фр. pallette - пластинка, планка) - графаға бөлінген, мысалы, кішкене квадраттарға бөлінген мөлдір тілімше көрініс сызбада немесе картада ауданды анықтау үшін қолданылады.

КІРІСПЕ

Дипломдық жұмыс тақырыбының өзектілігі. Мектеп геометрия курсын оқытудың негізгі мақсаттарының бірі - оқушыларға геометрияның теориялық негіздерін үйрету және оларды практикада қолдана білу дағдыларын меңгерту. Сонымен қатар оқушылардың логикалық ойлауын, дәлелдеу қабілетін, ой қорытуларды негіздей білу және кеңістіктік түсініктері мен елестету қабілеттерін қалыптастыру болып табылады [1], [2] .

Мектеп геометрия курсының көкейкесті мәселелері - курстың мазмұнының ғылыми құндылығын арттыру және оның негізінде оқушылардың пәнге деген қызығушылығын арттырып, өз бетінше іздену, шығармашылық іс-әрекеттерге тарту және т. с. с.

Геометрияның планиметрия бөлімінде жазықтықтағы геометриялық фигуралар жүйелі түрде оқытылады және жазық көпбұрыштарды сипаттайтын қасиеттер мен олардың шамаларына баса назар аударылады. Жазық фигураларды оқыту І-ІV сыныптарда қалыптасқан қарапайым геометриялық фигуралар жайлы түсініктерге негізделеді. Мұнда көптеген анықтамалар енгізіледі, мазмұнды теоремалар дәлелденеді, «қасиеттер» және «белгілер» ұғымдарын қалыптастыру бағытында жұмыстар жүргізіледі. Бастауыш сыныптарда жазық фигуралар арифметиканы оқытуда дидактикалық құралдар ретінде жақсы қолданылады. Мысалыға, 1-сыныпта көпбұрыштардың төбелерін, қабырғаларын, бұрыштарын санап, қабырғаларының ұзындықтарын өлшейді. 2-сыныпта тең квадраттарға бөлінген тіктөртбұрышты көбейтудің орын ауыстырымдылық заңын кескіндеуге пайдаланады және т. с. с [3] .

V-VI сыныптарда жазық көпбұрыштар арифметика және алгебра элементтерін оқытудағы дидактикалық құрал болып қана қоймай, сонымен қатар оқу объектісі болып табылады.

Ал VIІ сыныптан бастап геометрия курсында жазық көпбұрыштар мен олардың қасиеттерін оқыту белгілі бір дәрежеде танымдық функцияны да атқарады. Яғни оны оқу барысында оқушылар жеке мәселелердің тарихымен танысады, олардың адам өміріндегі орны мен ролін танып біледі. Сонымен қатар жазық көпбұрыштар мен олардың конфигурацияларын оқып-үйрену барысында басқа сыбайлас пәндерді, атап айтқанда физиканы, сызуды, еңбек сабағын оқуға қажетті білімді, іскерлікті және дағдыны қалыптастыру да іске асырылады.

Жазық көпбұрыштардың планиметрия курсында оқытылған қасиеттері мен белгілері стереометрия курсында, оның ішінде әсіресе көпжақтарды оқытуда кең қолдау табады. «Көпжақтар» тақырыбы орта мектептегі стереометрия курсының негізгілерінің бірі. Оны оқыту барысында оқушылардың планиметрия курсынан алған көпбұрыштар туралы білімдері, сонымен бірге стереометрияның Х сыныбындағы түзулер мен жазықтықтардың өзара орналасуы туралы білімдер жинақталып жүйеленеді. Бұл мұғалімнен планиметрия курсының да, стереометрияның өтілген тарауларын да қайталап алуда ерекше ұйымдастырушылықты талап етеді.

Көпжақтарды оқыту барысында оқушылардың кеңістіктік түсініктерін дамыту бағытындағы жұмыс жалғастырылады. Сондай-ақ, дұрыс көпбұрыштар мен дұрыс көпжақтар туралы білімдер оқушылардың пәнге деген қызығушылықтарын арттырып, оларға эстетикалық тәрбие беруде үлкен орын алады.

Сондықтанда, мектеп геометрия курсын оқытуда оқушыларға жазық көпбұрыштар мен көпжақтар, олардың қасиеттері, өзара орналасу жағдайлары және көпбұрыштардың конфигурациялары, көпжақтардың конфигурациялары туралы жүйеліде, терең білім беру барлық уақыттада күн тәртібінен түскен емес. Ал мектеп геометрия курсының негізгі тарауларының бірі болып табылатын «Көпбұрыштар» мен «Көпжақтар» тақырыбын оқушыларға саналы да, жүйелі түрде жеткізу үшін, болашақ математика мұғалімдері «Жоғары геометрия» курсында оқытылатын теориялық негідерін терең білуі керек.

Диплом жұмысының жаңалығы: мектеп геометрия курсында көпбұрыштар мен көпжақтарды оқытудың әдістемесі жасалды.

Жұмыстың практикалық құндылығы: болашақ математика мұғалімдері мен мектеп математика мұғалімдері үшін көмекші құрал ретінде пайдалануға болады.

Бұл дипломдық жұмыстың мақсаты: көпбұрыштар мен көпжақтардың теориялық негіздерін терең оқып-үйрену және олардың мектеп геометрия курсында баяндалу мүмкіндіктерін сараптау.

Бұл дипломдық жұмыстың міндеттері:

Екі өлшемді дөңес жазық фигуралардың қасиеттерін оқып-үйрену;
Дөңес көпбұрыштарды теориялық тұрғыдан анықтау және қасиеттерін қарастыру;
Дөңес көпбұрыштың қабырғалары арқылы анықталатын жарты жазықтықтар бойынша «Теңдеуін» беру;
Көпбұрыш және оның характеристикасы, қасиеттері туралы теориялық мәліметтерді қарастыру;
Мектеп геометрия курсында көпбұрыштар тақырыптарын оқытуда олардың теориялық негіздерін ескеру әдістемесін сараптау;
Тең фигуралардың бар болуын негіздеу және геометриялық теңдік ұғымының мәнін ашу, оны оқытудың әдістемесін сараптау;

Зерттеу нысаны: мектеп геометрия курсындағы көпбұрыштар мен көпжақтарды оқыту.

Диплом жұмыстың көлемі мен құрылымы: Дипломдық жұмыс үш бөлімді қамтиды: евклидтік кеңістіктегі көпбұрыштар мен көпжақтар теориясы, евклидтік кеңістіктегі көпбұрыштар мен көпжақтар теориясы, мектеп геометрия курсында көпбұрыштар мен көпжақтарды оқыту әдістемесі. Сонымен қатар, диплом жұмыста кіріспе, қорытынды, қолданылған әдебиеттер тізімі көрсетілген.

Жалпы дипломдық жұмыстың анықтамалық жазбасы барлығы 74 беттен тұрады, қолданылған әдебиеттер тізімі мен 32 суретті және 5 кестені құрайды.

1 ЕВКЛИДТІК КЕҢІСТІКТЕГІ КӨПБҰРЫШТАР МЕН КӨПЖАҚТАР ТЕОРИЯСЫ

1. 1 Дөңес фигуралар. Көпбұрыштар мен дөңес көпбұрыштар

Фигура және дөңес фигура

Математикада нүктелердің кез келген жиынын фигура дейді. Мысалы, А және В нүктелері мен олардың арасындағы түзу нүктелерінің жиынын АВ кесіндісі, бір түзудің бір жағында жатқан жазықтық нүктелерінің жиынын сол түзумен анықталатын жарты жазықтық дейді және т. с. с.

Фигураның барлық нүктесі бір жазықтықта жатса ол жазық фигура делінеді. Ол жазықтық фигура жазықтығы делінеді.

Фигураның барлық нүктесін қамтитын дөңгелек табылса, ол фигура шектелген, табылмаса шектелмеген делінеді. Үшбұрыш, кесінді шектелген, түзу, жарты жазықтық шектелмеген фигуралар.

Егер r>0 нақты сан болса,

\[{\widetilde{O}}_{0}\]

жазықтықтың нүктесі болса, онда ол жазықтықтың

\[\left|x_{0}{\tilde{\sigma}}\right| ,

\[\left|x_{0}{\tilde{\sigma}}\right|=r\]

\[\left|x_{0}{\tilde{\sigma}}\right|\leq r\]

болатын х нүктелердің жиынын, сәйкесінше, ашық дөңгелек, шеңбер, дөңгелек дейді. Центрі М болатын кез-келген ашық дөңгелекті бұл нүктенің аймағы дейді [4], [7] .

П жазықтықтың барлық нүктелерін, ол жазықтықта жатқан Ғ фигураға қатысты үшке бөлуге болады.

\[I\ \ \in\overline{{I}}\]

нүктесінен Ғ фигурада ең болмағанда бір аймағы болса (бірде-бір аймағы болмаса) оны Ғ- тің ішкі (сыртқы) нүктесі, ал М -нің кез-келген аймағында Ғ -те жататында, жатпайтында нүктелер болса, ол Ғ -тің шекаралық нүктесі делінеді. Шекаралық нүктелердің жиыны ол фиграның шекарасы делінеді, ішкі нүктелердің жиыны фигураның іші, ал сыртқы нүктелердің жиыны ол фигураны П -ге дейін толықтырушы делінеді.

Шекаралық нүктенің аймағына бұл фигураның нүктесінен басқа нүктелері енбесе, ол айрықша нүкте делінеді.

Шекарасы бар да, жоқта фигуралар болады. Шекарасы бар фигуралар тұйық, шекарасы жоқ фигуралар ашық фигуралар делінеді. Ашық фигуралар тек ішкі нүктелерден ғана тұрады.

Фигураның іші мен шекарасының біріктірмесін ол фигураның тұйықталуын

\[\overline{{F^{\prime}}}\]

арқылы белгілейік, 1. 1 суретте көрсетілген.

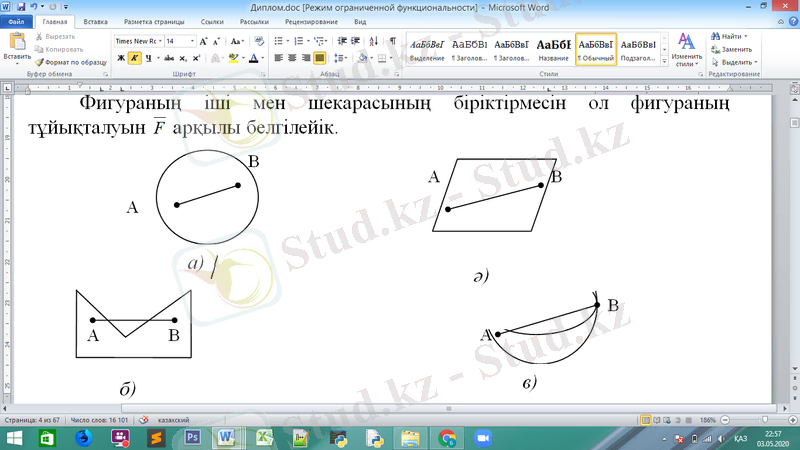
Сурет 1. 1 Тұйық және ашық фигуралар

\[\overline{{{P}}}_{1}\]

мен

\[F_{2}\]

фигуралар берілген

\[F_{1}\subset{\overline{{F_{2}}}}={\mathcal{D}}\]

\[\overline{{{F_{1}}}}\subseteq F_{2}=\mathcal{L}\]

болса

\[\overline{{{P}}}_{1}\]

мен

\[F_{2}\]

фигуралар айырылатын фигуралар делінеді. Ғ фигура айырылған екі фигураның бірігуі болмаса онда ол байламды делінеді.

Егер фигураның кез-келген екі нүктесін қосатын кесінді толығымен сол фигурада жататын болса, онда ол фигура дөңес, кері жағдайда дөңес емес делінеді.

Кесінді, үшбұрыш, параллелограм дөңес фигура болады 1-суреттегі а, ә) дөңес, б, в) ойыс фигуралар кескінделген. Берілген түзу бойында жатпайтын кемінде үш нүктесі болатын дөңес жазық фигураны екі өлшемді фигура дейді.

Екі өлшемді дөңес жазық фигураның қасиеттері.

1. Кез-келген екі өлшемді дөңес жазық фигураның шексіз көп ішкі нүктелері болады.

Шыныңда да Ғ екі өлшемді дөңес жазық фигура болса онда анықтама бойынша оның берілген түзуде жатпайтын кемінде 3 нүктесі болады. Олар А, В, С болсын, 1. 2 суретіне сәйкес. Е үшбұрыштың кез-келген бір ішкі нүктесі болсын

\[\dot{A}\dot{A}\;{\sf C}\;\dot{A}N=D\]

дейік. ста, Ғ -те дөңес фигуралар болатындықтан А, В, С нүктелерді қосатын кесінділер Ғ -те жатады. Сондықтан D -да Ғ -те жатады. Сөйтіп, Ғ -те шексіз көп нүкте болады.

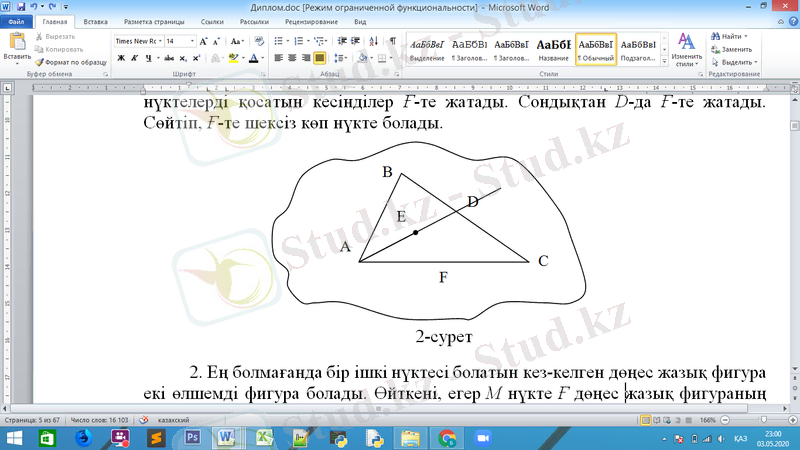
Сурет 1. 2. Үшбұрыш

2. Ең болмағанда бір ішкі нүктесі болатын кез-келген дөңес жазық фигура екі өлшемді фигура болады. Өйткені, егер М нүкте Ғ дөңес жазық фигураның ішкі нүктесі болса, онда М нүктенің аймағы болатын М центрлі дөңгелек Ғ -те жатады. Ал, дөңгелек бойында бір түзуде жатпайтын кемінде үш нүкте бар болады. Бұл Ғ екі өлшемді фигура болады деген сөз.

3. Егер А мен В дөңес жазық Ғ фигураның ішкі нүктелері болса, онда АВ кесіндінің барлық нүктесі Ғ -тің ішкі нүктесі болады.

4. Дөңес жазық Ғ фигура үшін А ішкі В шекаралық нүкте болса, онда АВ кесіндінің В -дан өзге барлық нүктелері Ғ -тің ішкі нүктесі болады. Егер А -да, В -да шекаралық нүктелер болса, онда АВ- ның А мен В дан өзге барлық нүктесі Ғ -тің ішкі нүктесі болады немесе АВ- ның барлық нүктесі шекаралық нүкте болады.

5. Егер l түзуі дөңес жазық Ғ фигураның бір ішкі нүктесі арқылы өтсе, онда l түзуінде Ғ фигураның екіден артық емес шекаралық нүктесі болады.

Ғ дөңес жазық фигурасының А шекаралық нүктесі болсын. А дан Ғ -тен әрбір ішкі нүктесін қосатын сәулелер жүргізейік (3, а - сурет), онда ол сәулелер жиыны не жарты жазықтық (3, а - сурет), не

\[180^{\circ}\]

тан кем бұрыш болатын аймақты (3 б - сурет) толтырады.

Бұл жағдайдың біріншісінде l түзуімен Ғ -ті бір ғана ортақ нүктесі болады және Ғ -тің барлық нүктесі l түзудің бір жағындағы жарты жазықтықта жатады. l -ді дөңес Ғ фигураның тірек түзуі дейді. А -дан жүргізілген l ден басқа түзу Ғ -ті екіге бөледі. Сондықтан олар тірек түзу болмайды.

Екінші жағдайда Ғ фигура ВАС бұрыштын ішкі бөлігінде жатады. Бұл кезде ВАС бұрыштын ішкі нүктесінен өтпейтін кез-келген түзу (3б - сурет) және АВ, АС түзулер Ғ үшін тірек түзу болады. Бір ғана тірек түзу өтетін шекаралық нүктені жай нүкте дейді, ол нүктеден тірек түзуді Ғ -ке жанама түзу дейді. Ал, бірнеше тірек түзу өтетін нүктені ерекше нүкте дейді және АВ мен АС бұл кезде жартылай жанама түзулер делінеді. Олар арасындағы ВАС бұрышты Ғ -тен А нүктедегі шекаралық бұрышы дейді. Ол

\[\ U\]

болса,

\[180-a\]

бұрыш Ғ -тен А нүктедегі сыртқы бұрышы делінеді. Дөңгелектің әрбір шекаралық нүктесі кәлімі нүкте, үшбұрыштын әрбір төбесі ерекше нүкте болады. Кез-келген жазық дөңес фигураның ерекше нүктелері санаулы ғана болады, ол нүктелердегі сыртқы бұрыштардың қосындысы 2d -дан артпайды.

Сурет 1. 3. Жазық фигуралар

Кез-келген дөңес жазық фигураның ең алыс екі нүктесінің арасы ол фигураның диаметрі делінеді. Үшбұрыштың ең ұзын қабырғасы оның диаметрі болады. Фигураның АВ диаметрі болса, онда А, В нүктелерден АВ -ға жүргізілген перпендикуляр түзулер ол фигураның тірек түзулері болады.

Фигураның қандайда бір d түзуге параллель етіп жүргізілген екі тірек түзуінің арасын фигураның d бағыттағы ені дейді. Ол ең үлкен болғанда диаметрге тең болады. Бір фигураның әртүрлі бағыттағы ендерінен әртүрлі болуы мүмкін. Олардың ең кішісін фигураның ені дейді. Шектердің ені мен диаметрі тең болады. Ондай фигураны тұрақты енді фигура дейді. Екі дөңес фигураның нүктелерінің ара қашықтықтарының ең төменгі шекарасын сол екі фигураның арасы дейді. Бірнеше фигураның ортақ нүктелерінің жиынын ол фигуралардың қимасы дейді.

1-теорема. Егер А нүктесі

\[\overline{{{P}}}_{1}\]

мен

\[F_{2}\]

фигуралардың екеуініңде ішкі нүктесі болса, онда ол олардың

\[F_{1}\cap F_{2}\]

қимасыныңда ішкі нүктесі болады, ал біреуінің ішкі, екіншісінің шекаралық нүктесі болса, онда ол олардың қимасының шекаралық нүктесі болады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.