Теңсіздіктерді дәлелдеудің теориясы мен әдістері


Ж. Досмұхамедов атындағы педагогикалық колледж
Математика кафедрасы
Курстық жұмыс
Тақырыбы:
Теңсіздіктерді дәлелдеу
Орындаған: 4 а МК тобы
студенті
Мухтарова Гулдана
Жетекшісі: Жұматова М. С
Орал-2014ж.
Мазмұны:
1. Кіріспе . . . 6
2. Тарихи шолу . . . 8
3. Теңсіздікті анықтамасының көмегімен дәлелдеу әдісі . . . 18
4. Теңсіздіктің жасанды жолмен дәлелдеу әдісі . . . 20
5. Теңсіздікті кері жору әдісімен дәлелдеу . . . 23
6. Теңсіздікті математикалық индукция әдісімен дәлелдеу . . . 24
7. Математикалық орта ұғымы туралы . . . 26
8. Практикалық бөлім . . . 29
9. Қорытынды . . . 35
10. Қолданылған әдебиеттер . . . 36
Жоспар:
І. Кіріспе .
ІІ. Тарихи шолу
2. 1. Теңсіздікті анықтамасының көмегімен дәлелдеу
әдісі.
2. 2. Теңсіздіктің жасанды жолмен дәлелдеу әдісі
2. 3. Теңсіздікті кері жору әдісімен дәлелдеу.
2. 4. Теңсіздікті математикалық индукция әдісімен
дәлелдеу
2. 5. Математикалық орта ұғымы туралы
ІІІ. Практикалық бөлім
ІV. Қорытынды
І. Кіріспе бөлім
Зерттеу өзектілігі. Мектеп математика курсында теңсіздік тақырыбы елеулі орын алар математиканың ерекше бөлімі деуге болады.
Теңсіздік алғаш мектеп математикасында қолданып, даму бағыттарының негізін салушылардың бірі, атақты француз математигі - Луи Огюстен Коши. Мектеп математикасында Коши есебі бірден-бір үшбұрыш тесіздігімен байланысты. Яғни, үшбұрыштың кез-келген қабырғасы, қалған екі қабырғаларының қосындысынан үлкен бола алмайтындығы туралы теорема.
Математикада оқушыларға теңсіздік тақырыбының қыр-сырын түсіндіру барысында, алғаш қадам - сандарды салыстырудан бастау алады. Өйткені, бұл ұғым оқушыларға бастауыш сыныптардан таныс. Теңсіздік тақырыбы мектеп математикасында «Сандық теңсіздіктер» деп аталатын тараумен 6-сыныпта беріледі, курс жоғарылаған сайын күрделене түседі.
Жалпы мектеп курсында теңсіздік ұғымы жүйелі түрде оқытылады. Теңсіздік тақырыбына есептер шығаруда әр түрлі әдістер қолданылады.
Теңсіздіктерді шешуде қиындық тудыратын тақырыптардың бірі - сандық теңсіздіктерді шешудің ұтымды, қолайлы әдісін пайдалана отырып дәлелдеу.
теңсіздік ұғымын, оның қасиеттерін қарастыру және оларды дәлелдеу әдістерін пайдалану, алған білімдерді есептер шығару барысында қолдана білуге үйрету.
- теңсіздік қасиеттері мен түрлеріне анықтама беру;
- теңсіздіктерді теориялық тұрғыдан қарастыру;
- есептерді орындауда теңсіздікті қолдануды айқындау;
- теңсіздіктерді шешудің бірнеше әдістерін пайдалану.
бірнеше тәсілдерін көрсете білсек, онда теңсіздіктерді шешуде бірнеше тиімді әдістерін білер еді.
Зерттеудің көздері : математика, физика және информатика ғалымдарының еңбектері, мектептің білім беру стандарты, оқу бағдарламалары, оқулықтар.
Зерттеу әдістері: математика, физика және информатика әдебиеттеріне теориялық талдау жасау; кері жору және математикалық индукция.
Ғылыми жаңалығы: Оқушыларға теңсіздіктерді шешуде үйретуге қажетті теориялық білімі мен біліктіліктерін, дағдысын жетілдіріп, бекіте түсетін арнаулы мысалдар және олардың шешу жолдары көрсетілді.
Практикалық маңызы: Зерттеу жұмысындағы тұжырымдарды, мысалдарды мектеп оқушылары, орта, арнаулы және жоғары орындарының студенттеріне қолдануға болады.
Зерттеу жұмысының құрылымы: Курстық жұмыс кіріспеден, негізгі (теориялық және практикалық) бөлімнен, қорытындыдан және әдебиеттер тізімінен тұрады.
ІІ. Тарихи шолу.
Мектеп курсында теңсіздік тақырыбы мен олардың қасиеттері, және осы қасиеттерді көрсететін теоремалар кең қолдау табады.
Мектеп математика курсында рационал, модулі бар, иррационал, көрсеткіштік, логарифмдік теңсіздіктерді шешу түрлері оқытылады. Олардың ерекшеліктері мен шешу әдістері маңызды рөл атқарады.
Теңсіздіктер туралы мағлұматтар бұдан кейін теңсіздік анықтамасының көмегімен, жасанды жолмен, кері жору және математикалық индукция әдісімен дәлелдеу түрлерін қарастырады. Басты назар дәлелдеу барысында қолданылатын негізгі элементтер мен мақсатқа жету жолдарына және іскерлігін қалыптастыра білуге үйрететін есептерге аударылуы керек.
Теңсіздік алғаш мектеп математикасында қолданып, даму бағыттарының негізін салушылардың бірі, атақты француз математигі - Луи Огюстен Коши.
 Луи Огюстен Коши (1789-1857) - атақты француз математигі. Ол математиканың комплекс айнымалы функциялар теориясы, функциялар анализі, дифференциалдық теңдеулер, және теңсіздіктер сынды облысында ғажап теоремалар дәлелдеген.
Луи Огюстен Коши (1789-1857) - атақты француз математигі. Ол математиканың комплекс айнымалы функциялар теориясы, функциялар анализі, дифференциалдық теңдеулер, және теңсіздіктер сынды облысында ғажап теоремалар дәлелдеген.
Коши өткен ғасырдың 20-шы жылдарында анализ бастамаларына берік іргетасын қалауда сенімді қадам жасаған математиктердің бірі.
Ол - математика курсының даму тарихын белгілі ғажап теоремаларды дәлелдеп, ғалымда өшпес із қалдырған ұлы тұлға. Оның еңбектерінің ішінде векторлар арасындағы бұрыш, үшбұрыш теңсіздігі, скаляр көбейтінділі комплекс жазықтық сынды математикалық тақырыптар бойынша дәлелденген теоремаларының алатын орны бір бөлек.
Мектеп математикасындағы Коши есебі бірден- бір үшбұрыш теңсіздігімен байланысты. Яғни, үшбұрыштың кез- келген қабырғасы, қалған екі қабырғаларының қосындысынан үлкен бола алмайтындағы туралы теорема.
Математикада оқушыларға теңсіздік тақырыбының қыр- сырын түсіндіру барысында, алғаш қадам сандарды салыстырудан бастау алады. Өйткені бұл ұғым оқушыларға бастауыш сынытардан таныс. Теңсіздік тақырыбы мектеп математикасында «Сандық теңсіздіктер» деп аталатын тараумен 6-сыныпта беріледі.
Біз кез-келген а және в сандарын салыстыра аламыз және салыстыру нәтижелерін =, >, < белгілерін пайдалана отырып, теңдік немесе теңсіздік түрінде жаза аламыз.
Кез- келген а және в сандары үшін мына қатынастардың тек біреуі ғана орындалады: a=в, а>в.
Мысалдар қарастырайық:
1.
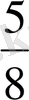 және
және
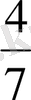 бөлшектерін салыстырайық. Ол үшін оларды ортақ бөлімге келтіреміз.
бөлшектерін салыстырайық. Ол үшін оларды ортақ бөлімге келтіреміз.
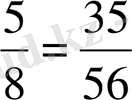 және
және
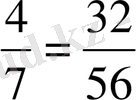
 болғандықтан,
болғандықтан,
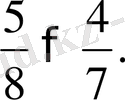
2.
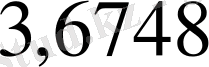 және
және
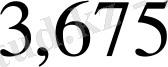 ондық бөлшектерін салыстырайық. Бірлік, ондық және жүздік үлестер разрядтарындағы цифрлары бірдей, ал бірінші бөлшектің мыңдық үлестерінде
ондық бөлшектерін салыстырайық. Бірлік, ондық және жүздік үлестер разрядтарындағы цифрлары бірдей, ал бірінші бөлшектің мыңдық үлестерінде
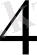 цифры, ал екінші бөлшекте 5 цифры жазылған.
цифры, ал екінші бөлшекте 5 цифры жазылған.
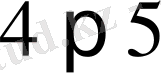 болғандықтан,
болғандықтан,
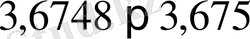 .
.
3.
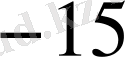 және
және
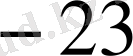 теріс сандарын салыстырайық. Бірінші санның модулі екіншінің модулінен кіші. Олай болса, бірінші сан екінші саннан үлкен, яғни
теріс сандарын салыстырайық. Бірінші санның модулі екіншінің модулінен кіші. Олай болса, бірінші сан екінші саннан үлкен, яғни
 .
.
Біз сандардың нақты түріне қарай салыстырудың белгілі бір тәсілін пайдаландық. Алайда, сандарды салыстырудың барлық жағдайын қамтитын тәсілдің болғаны қолайлы. Ол тәсілдің мәнісі мынадай:
сандардың айырмасын есептеп шығарып, оның оң сан, теріс сан немесе нөл болғандығын айқындайды. Сандарды салыстырудың бұл тәсілі келесі анықтамаға негізделген.
Анықтама
:
Егер
 айырмасы оң болса, онда
айырмасы оң болса, онда
 саны
саны
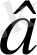 санынан үлкен болады, егер
санынан үлкен болады, егер
 айырмасы теріс болса, онда
айырмасы теріс болса, онда
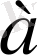 саны
саны
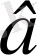 санынан кіші болады.
санынан кіші болады.
Егер
 айырмасы нөлге тең болса, онда
айырмасы нөлге тең болса, онда
 және
және
 сандарының тең болатынын ескертейік.
сандарының тең болатынын ескертейік.
Мектеп математика курсында теңсіздік тақырыбымен қатар оладың қасиеттері де маңызды орын алады. Теңсіздіктердің қасиеттерін көрсететін теоремаларды қарастырайық.
1-теорема:
Егер
 болса, онда
болса, онда
 болады, егер
болады, егер
 болса,
болса,
онда
 болады.
болады.
Шынында да, егер
 айырмасы - оң сан болса, онда
айырмасы - оң сан болса, онда
 айырмасы теріс сан болады және керісінше.
айырмасы теріс сан болады және керісінше.
2- теорема
: Егер
 және
және
 болса, онда
болса, онда
 болады.
болады.
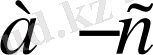 айырмасының теріс болатынын дәлелдейік. Осы айырмаға
айырмасының теріс болатынын дәлелдейік. Осы айырмаға
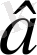 және
және
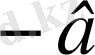 сандарын қосайық және қосылғыштарын топтастырайық:
сандарын қосайық және қосылғыштарын топтастырайық:
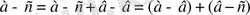
Шарт бойынша
 және
және
 . Сондықтан,
. Сондықтан,
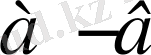 және
және
 қосылғыштары да теріс сандар. Демек, бұлардың қосындысы да теріс сан болып табылады. Олай болса,
қосылғыштары да теріс сандар. Демек, бұлардың қосындысы да теріс сан болып табылады. Олай болса,
 болады.
болады.
3-теорема
: Егер
 және
және
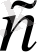 кез-келген сан болса, онда
кез-келген сан болса, онда
 болады.
болады.
 айырмасын түрлендірейік:
айырмасын түрлендірейік:
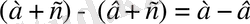 . Шарт бойынша
. Шарт бойынша
 , сондықтан
, сондықтан
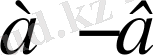 -теріс сан. Демек,
-теріс сан. Демек,
 айырмасы да теріс сан болады. Олай болса,
айырмасы да теріс сан болады. Олай болса,
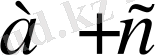
 .
.
Сонымен, егер тура теңсіздіктің екі жақ бөлігіне де бірдей сан қосылса, онда тура теңсіздік шығады.
4- теорема
: Егер
 және
және
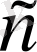 - оң сан болса, онда
- оң сан болса, онда
 болады. Егер
болады. Егер
 және
және
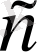 -теріс сан болса, онда
-теріс сан болса, онда
 болады.
болады.
 айырмасын көбейтінді түрінде жазайық:
айырмасын көбейтінді түрінде жазайық:
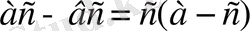 .
.
 болғандықтан
болғандықтан
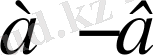 теріс сан болады. Егер
теріс сан болады. Егер
 болса, онда
болса, онда
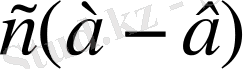 көбейтіндісі теріс сан болады, сондықтан
көбейтіндісі теріс сан болады, сондықтан
 . Егер
. Егер
 болса, онда
болса, онда
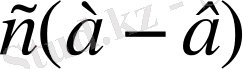 көбейтіндісі оң сан болады, сондықтан
көбейтіндісі оң сан болады, сондықтан
 .
.
Бөлуді бөлгішке кері санға көбейтумен алмастыруға болғандықтан, осындай қасиет бөлу үшін де дұрыс болады.
Сонымен, егер тура теңсіздіктің екі жақ бөлігі бірдей оң санға көбейтілсе немесе бөлінсе, онда тура теңсіздік шығады;
Егер тура теңсіздіктің екі жақ бөлігі бірдей теріс санға көбейтілсе немесе бөлінсе және де теңсіздіктің таңбасы қарама-қарсы таңбаға өзгертілсе, бұл жағдайда да тура теңсіздік шығады.
Салдар
:
Егер
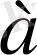 мен
мен
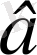 - оң сандар және
- оң сандар және
 болса,
болса,
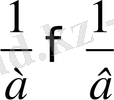 болады.
болады.
Мектеп математика курсында теңсіздіктің келесі түрлері оқытылады:
» рационал теңсіздіктер
» модуль таңбасы бар теңсіздіктер
» иррационал теңсіздіктер
» көрсеткіштік теңсіздіктер
» логарифмдік теңсіздіктер
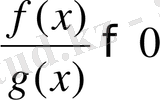 теңсіздігін
рационал теңсіздіктің
стандарт түрі деп атайды.
теңсіздігін
рационал теңсіздіктің
стандарт түрі деп атайды.
Мұндағы
 белгісінің орнында,
белгісінің орнында,
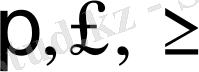 белгілері тұруы мүмкін.
белгілері тұруы мүмкін.
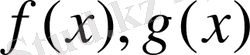 - көпмүшелер.
- көпмүшелер.
Рационал теңсіздіктерді шешуге тоқталып кетелік:
а) Квадрат теңсіздіктерді шешу.
Квадрат теңсіздіктерді шешу барысында квадрат үшмүшенің түбірлерін табуға тура келеді. Квадрат үшмүшенің дискриминанты нөлден үлкен болған жағдай қиындық келтірмейді, ал дискриминант нөлден кіші болған жағдайда кейбір оқушылар «теңсіздіктің жауабы жоқ» деген қате қорытынды жасайды. Бұл жерде теңсіздік шешіп отырғанымызды ұмытпауымыз керек. Дискриминант теріс болған жағдайда квадрат теңдеудің нақты түбірлері болмайды. Ал, теңсіздікті шешкенде жағдай өзгеше. Бұл жағдайда бізге квадрат үшмүшеннің геометриялық кескіні болып есептелетін параболаның графигі көмекке келеді. Берілген парабола, сан осін қандай да екі нүктеде қияды. Теңсіздікті шешкенде - бізге үшмүшенің графигін сызу қажеттігі жоқ. Тек үшмүшенің таңбасының өзгеру схемасын ирек сызықпен сан осінде кескіндеу жеткілікті. Бұдан біз қай аралықта, теңсіздік қандай таңбаны анықтайтындығын көреміз, яғни теңсіздікті интервалдар әдісімен шешеміз.
Көпмүшенің таңбасын сан осі арқылы анықтауды - интервалдар әдісі деп атайды.
Интервалдар әдісі - рационал теңсіздіктерді шешудің ең бір тиімді әдісі болып есептелінеді.
Интервалдар әдісінің мағынасы мынадай:
1) Егер теңсіздік стандарт түрде берілмесе, берілген теңсіздікті стандарт түрге келтіреміз.
2) Бөлшектің алымындағы өрнектің түбірлерін тауып, оларды сан осінде белгілейміз.
3) Сан осін белгілеген нүктелерді қиып өтетіндей график сызамыз.
Егер бөлшектің алымындағы және бөліміндегі көпмүшелердегі белгісіздердің ең үлкен дәрежелі мүшелерінің таңбалары бірдей болса, онда графигін сан осінің жоғарғы жағынан бастап сызамыз. Ал, олардың таңбалары әр түрлі болса, онда графикті сан осінің төменгі жағынан бастап сызамыз.
4) Егер берілген теңсіздік
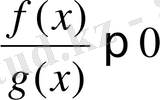 немесе
немесе
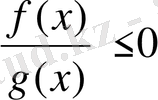 түрінде болса, оның шешімі теріс таңбалы инервалдар болады. Егер теңсіздік
түрінде болса, оның шешімі теріс таңбалы инервалдар болады. Егер теңсіздік
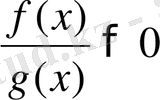 немесе
немесе
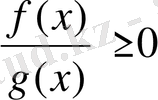 түрінде берілсе, оның шешімі оң таңбалы интервалдар болады.
түрінде берілсе, оның шешімі оң таңбалы интервалдар болады.
5) Егер теңсіздік
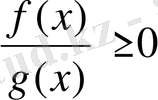 немесе
немесе
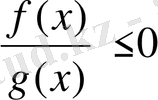 түрінде берілсе, онда бөлшектің алымының түбірлері теңсіздіктің шешіміне кіреді.
түрінде берілсе, онда бөлшектің алымының түбірлері теңсіздіктің шешіміне кіреді.
Ескерту: Бөлшектің бөлімінің түбірлері теңсіздік шешіміне ешқашан кірмейді.
Мысалы:
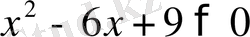 теңсіздігін шешейік.
теңсіздігін шешейік.
Шешуі: Квадрат үшмүшенің дискриминантын табайық: D=0. Ендеше,
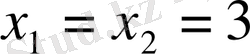 . Интервалдар әдісін қолдансақ,
. Интервалдар әдісін қолдансақ,
Қисық сызық сан осін
 нүктесінде екі рет қиып өтеді, өйткені екі түбірдің екеуі де үшке тең.
нүктесінде екі рет қиып өтеді, өйткені екі түбірдің екеуі де үшке тең.
Теңсіздіктің шешімі:
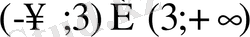
Модуль таңбасы бар теңсіздіктерді шешудің бірнеше әдісі бар:
1) модульді сан осіндегі екі нүктенің ара қашықтығы ретінде алып, теңсіздікті шешу;
2) теңсіздіктің екі жағын квадраттау әдісі.
Берілген теңсіздік пен оның квадратталған өрнегінен - құралған теңсіздіктер шығады. .
3) Модульдің анықтамасына негізделген әдіс - теңсіздікті, теңдеулер жүйесімен алмастыру.
Берілген модулі бар теңсіздікті оң және теріс таңбалы модульсіз теңсіздіктерге алмастырып, жүйе құрып шешеміз.
Мысалы:
 теңсіздігін шешу керек.
теңсіздігін шешу керек.
Шешуі:
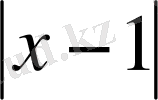 - ді сан осіндегі
- ді сан осіндегі
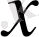 және 1 нүктелерінің ара қашықтығы деп қарастырамыз. Теңсіздіктің шарты бойынша сан осіндегі 1 нүктесінен 3 бірліктен кіші қашықтықта жатқан нүктелердің бәрін табуымыз қажет.
және 1 нүктелерінің ара қашықтығы деп қарастырамыз. Теңсіздіктің шарты бойынша сан осіндегі 1 нүктесінен 3 бірліктен кіші қашықтықта жатқан нүктелердің бәрін табуымыз қажет.
Суретте көрсетілгендей етіп, сан осінде 1 нүктесін және одан үш бірлік қашықтықта жататын екі нүктенің біреуі 1 нүктесінің оң жағында, екіншісі оның сол жағында болатындай етіп белгіленеді.
Сонда -2, 1, 4 нүктелері белгіленген болып шығады, сөйтіп мысалдың жауабы: (-2; 4)
Иррационал теңсіздіктерді шешу үшін оларды өзімен пара-пар рационал теңсіздіктер жүйесіне келтіреді.
Квадрат түбірдің астындағы өрнек теріс санға тең болмауы керек.
Бөлшектің алымында немесе бөлімінде түбір кездесетін теңсіздіктерді шешкенде алдымен:
1) айнымалының қабылдай алатын мәндерінің облысын тауып алу қажет. Ол үшін, бөлшектің бөлімінде тұрған өрнек нөлге тең болмауы және түбір астындағы өрнек теріс сан болмауы керек екендігі қатаң ескеріледі;
2) теңсіздікті шешеді;
3) айнымалының қабылдай алатын мәндерінің облысын ескере отырып, теңсіздік жауабы табылады.
Мысал:
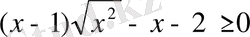 теңсіздігін шешу керек.
теңсіздігін шешу керек.
Шешуі: Квадрат түбірдің астындағы өрнектің мәні теріс сан болмайтынын ескерсек,
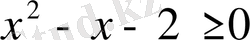 болуы шарт. Түбірдің астында тұрған квадрат үшмүшенің түбірлерін табайық:
болуы шарт. Түбірдің астында тұрған квадрат үшмүшенің түбірлерін табайық:
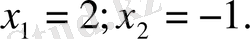
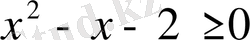 теңсіздігін шешіп,
теңсіздігін шешіп,
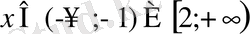 табамыз. Берілген теңсіздік үшін
табамыз. Берілген теңсіздік үшін
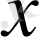 -тің қабылдай алатын мәндерінің облысы:
-тің қабылдай алатын мәндерінің облысы:
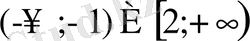
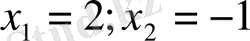 мәндерін берілген теңсіздікке қойсақ, нөлге тең шарты шығады, яғни бұл мәндер берілген теңсіздіктің шешімдері болады.
мәндерін берілген теңсіздікке қойсақ, нөлге тең шарты шығады, яғни бұл мәндер берілген теңсіздіктің шешімдері болады.
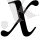 -тің 1-ден кіші мәндерінде және 2-ден үлкен мәндерінде
-тің 1-ден кіші мәндерінде және 2-ден үлкен мәндерінде
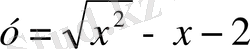
Функциясының мәні оң болады.
Берілген теңсіздік
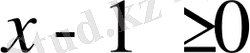 теңсіздігіне пара-пар болғандықтан, осы теңсіздіктің шешуін қарастырайық.
теңсіздігіне пара-пар болғандықтан, осы теңсіздіктің шешуін қарастырайық.
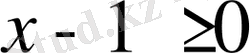 , бұдан
, бұдан
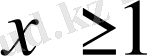 . Берілген теңсіздік үшін
. Берілген теңсіздік үшін
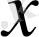 -тің қабылдай алатын мәндері минус бір, екі және минус бірден кіші, екіден үлкен аралықтар. Ендеше, берілген теңсіздіктің шешуі
-тің қабылдай алатын мәндері минус бір, екі және минус бірден кіші, екіден үлкен аралықтар. Ендеше, берілген теңсіздіктің шешуі
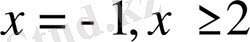 болып шығады.
болып шығады.
Белгісізі дәреже көрсеткішінде болып келетін теңсіздіктерді көрсеткіштік теңсіздіктер деп атайды.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz