Периодты дифференциалдық жүйенің периодты шешімінің түрі

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 27 бет
Таңдаулыға:

Қазақстан Республикасының Білім және ғылым министрлігі

Әл-Фараби атындағы Қазақ ұлттық Университеті

Асанова М.Б.

СЫЗЫҚТЫҚ ЕМЕС ПЕРИОДТЫ ДИФФЕРЕНЦИАЛДЫҚ ЖҮЙЕНІҢ ОРНЫҚТЫ ПЕРИОДТЫ ШЕШІМІН ҚҰРУ

ДИПЛОМДЫҚ ЖҰМЫС

мамандығы 5B060100 - Математика

Алматы 2019
Қазақстан Республикасының Білім және ғылым министрлігі

Әл-Фараби атындағы Қазақ ұлттық университеті

Дифференциалдық теңдеулер және басқару теориясы кафедрасы

Қорғауға жіберілді
Кафедра меңгерушісі
ф.-м.ғ.к.,доцент м.а._________________Х.Хомпыш

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы:СЫЗЫҚТЫҚ ЕМЕС ПЕРИОДТЫ ДИФФЕРЕНЦИАЛДЫҚ ЖҮЙЕНІҢ ОРНЫҚТЫ ПЕРИОДТЫ ШЕШІМІН ҚҰРУ

мамандығы 5B060100 - Математика

ОрындағанМ.Б.Асанова

Ғылыми жетекші
п.ғ.д.,математика профессорыЖ.Сулейменов

Норма қадағалаушыГ.Т.Көрпебай

Алматы, 2019
РЕФЕРАТ

Бітіру жұмысы 40 бет, 2 бөлім, кіріспе, қорытынды және пайдаланылған әдебиет тізімін қамтиды.
Бірінші бөлімде орнықтылық, асимптотикалық орнықтылық, шартты орнықтылық, бірқалыпты орнықтылық түсініктері және бірінші жуықтау бойынша орнықтылық туралы Ляпуновтың теоремасы мен бірінші жуықтау бойынша бірқалыпты орнықтылық туралы Персидскийдің теоремасы келтірілген.
Екінші бөлімде периодты дифференциалдық жүйенің периодты шешімін құрудың бір тиімді әдісі берілген. Ол үшін Коши, шекаралық және Грин функциялары пайдаланылады. Қарастырылатын жүйенің нөлдік шешімінің бірінші жуықтау бойынша бірқалыпты асимптотикалық орнықты болатыны дәлелденеді.
Түйін сөздер: периодты функция, периодты шешім, Коши матрицасы, шекаралық матрица, Грин матрицасы, периодты шекаралық есеп, орнықтылық, шартты орнықтылық, бірінші жуықтау бойынша орнықтылық.
РЕФЕРАТ

Выпускная работа содержит 40 страниц, 2 раздела, введение, заключение и список использованной литературы.
В первой части приводятся понятия устойчивости, асимптотической устойчивости, условной устойчивости, равномерной устойчивости и теорема Ляпунова об устойчивости по первому приближению и теорема Персидского о равномерной устойчивости по первому приближению.
Во втором разделе предаставлен один эффективный метод построения периодического решения дифференциальной системы. Для этого используются функции Коши, граничные и Грин. Доказывается, что нулевое решение рассматриваемой системы является равномерным асимптотически устойчивым по первому приближению.
Ключевые слова: периодическая функция, периодическое решения, матрица Коши, пограничная матрица, матрица Грина, периодический пограничный расчет, устойчивость, условная устойчивость, устойчивость по первому приближению.

ABSTRACT

The publication of the work contains 40 pages, 2sections, instroduction, conclusion and references.
The first part presents the concepts of stability, asymptotic stability, conditional stability, uniform stability and Lyapunov's theorem on stability on the first approximation and Persian theorem of uniform stability on the first approximation .
The second section presents one effective method for constructing a periodic solution of a differential system. Cauchy, boundary and green functions are used for this purpose. It is proved that the zero solution of the considered system is uniform asymptotically stable on the first approximation.
Keywords: periodic function, periodic solutions, Cauchy matrix, boundary matrix, green matrix, periodic boundary calculation, stability, conditional stability, stability on the first approximation.

МАЗМҰНЫ

КІРІСПЕ6

1 ОРНЫҚТЫЛЫҚ ТЕОРИЯСЫ. БІРІНШІ ЖУЫҚТАУ БОЙЫНША ОРНЫҚТЫЛЫҚ.7

1.1 Орнықтылықтың негізгі анықтамалары.7
1.2 Бірінші жуықтау бойынша орнықтылық туралы Ляпунов теоремасы11
1.3 Бірінші жуықтау бойынша бірқалыпты орнықтылық туралы Персидский теоремасы20

2 СЫЗЫҚТЫ ЕМЕС ПЕРИОДТЫ ДИФФЕРЕНЦИАЛДЫҚ ЖҮЙЕНІҢ ОРНЫҚТЫ ПЕРИОДТЫ ШЕШІМІН ТАБУ30

2.1 Периодты дифференциалдық жүйенің периодты шешімінің түрі30
2.2 Сызықты емес жүйенің шартты асимптотикалық орнықты болуы34

ҚОРЫТЫНДЫ38

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТ ТІЗІМІ39

КІРІСПЕ

Зерттеу тақырыбының өзектілігі. Дипломдық жұмыста периодты дифференциалдық жүйенің периодты шешімін құрудың тиімді әдісі қарастырылады. Қарастырылатын жүйенің нөлдік шешімінің белгілі шарттар орындалғанда бірінші жуықтау бойынша бірқалыпты асимптотикалық орнықты болатыны көрсетіледі.
Шешімнің орнықтылығы дифференциалдық теңдеулерде қолданысқа керекті негізгі материалдардың бірі болып саналады. Шешімдердің сапасын: орнықтылығын, периодтылығын, асимптотикалық қасиетің анықтау өте маңызды мәселе.
Зерттеудің мақсаты. Жұмыстың негізгі мақсаты: сызықтық емес периодты дифференциалдық жүйенің орнықты периодтық шешімінің бар болуын көрсету. Мақсатты жүзеге асыру үшін төмендегідей негізгі міндеттерді шешу көзделінді:
-дифференциалдық жүйенің периодты шешімін құру;
-Коши, шекаралық және Грин функцияларын құру және пайдалану;
-сызықтық периодты жүйенің периодты шешімін құру;
-сызықтық емес периодты жүйенің периодты шешімінің бар болу және бірінші жуықтау бойынша асимптотикалық орнықты болатыны дәлелденеді;
Зерттеу пәні. Зерттеудің негізгі пәні дифференциалдық теңдеудің сапалық теориясы болып саналады.
Зерттеу әдістері. Бітіру жұмысы Четаев Н.Г.[2], Малкин И.Г.[3], Персидский К.П.[5], Демидович Б.П.[7], және т.б. ғалымдардың жұмыстары пайдаланылған. Жұмыста периодтылық, орнықтылық, асимптотикалық орнықтылық, шартты орнықтылық, Ляпунов теоремасы, бірінші жуықтау бойынша бірқалыпты орнықтылық туралы Персидский теоремалары қолданылған.
Практикалық және теориялық құндылығы.Сызықтық емес периодты жүйе қарастыру. Осындай жүйенің шартты орнықты периодты шешімін табу.
Диссертациялық жұмыстың қысқаша мазмұны. Бірінші бөлімде орнықтылық, асимптотикалық орнықтылық, шартты орнықтылық, бірқалыпты орнықтылық түсініктері және бірінші жуықтау бойынша орнықтылық туралы Ляпуновтың теоремасы мен бірінші жуықтау бойынша бірқалыпты орнықтылық туралы Персидскийдің теоремасы келтірілген.
Екінші бөлімде периодты дифференциалдық жүйенің периодты шешімін құрудың бір тиімді әдісі берілген. Ол үшін Коши ,шекаралық және Грин функциялары пайдаланылады. Қарастырылатын жүйенің нөлдік шешімінің бірінші жуықтау бойынша бірқалыпты асимптотикалық орнықты болатыны дәлелденеді.

1 ОРНЫҚТЫЛЫҚ ТЕОРИЯСЫ. БІРІНШІ ЖУЫҚТАУ БОЙЫНША ОРНЫҚТЫЛЫҚ.

1.1 Орнықтылықтың негізгі анықтамалары.

Дифференциалдық теңдеулердің қалыпты жүйесін қарастырайық:

(1)

Мұндағы 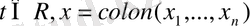- белгісіз вектор - функция, 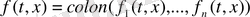- берілген вектор - функция. Бұл функция белгілі бір ашық 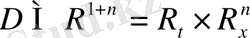облысында 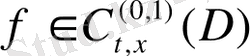шартын қанағаттандырады. Осы жағдайда 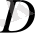облысының кез-келген нүктесі арқылы берілген (1) жүйенің жалғыз ғана шешімі өтеді.
Анықтама 1.1. Егер және бастапқы 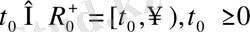мәні үшін 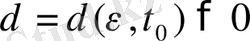саны табылып, берілген (1) жүйенің 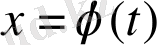шешімі мен келесі теңсіздікті

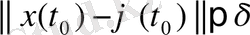(2)

қанағаттандыратын барлық 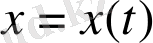шешімдері

1) 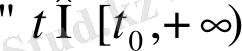мәндерінде анықталса (

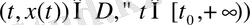
2) 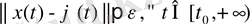(3)

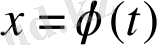
теңсіздігін қанағаттандырса, онда 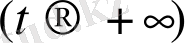шешімі Ляпунов бойынша орнықты деп аталады([3],[7]). Орнықтылықтың геометриялық мағынасы: кез келген бастапқы 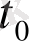мезетінде 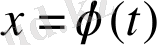интегралдық қисығына жақын (қашықтығы 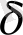-ден кем) қарастырылып отырған (1) жүйенің кез келген интегралдық қисықтары шексіз ұзартылмалы ( 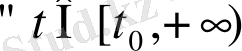анықталса) және 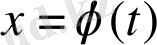қисығын айналдыра құрған мейлінше тар 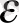- түтікшенің ішіне толығынан орналасса, онда шешімі орнықты деп аталады.
Анықтама 1.2. Егер 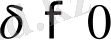санын бастапқы 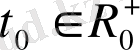мезетінен тәуелсіз деп (яғни 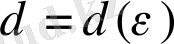) алсақ, орнықтылық бірқалыпты деп аталады.
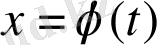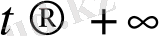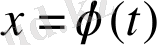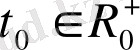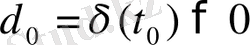Анықтама 1.3. () шешімі асимптотикалық орнықты деп аталады [8], егер шешімі Ляпунов бойынша орнықты болса және кез келген үшін саны табылып, 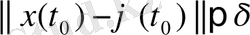теңсіздігін қанағаттандыратын барлық 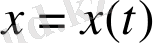шешімдері үшін келесі теңдік:

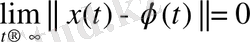
орындалатын болса.
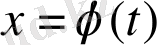Асимптотикалық орнықтылық ұғымының геометриялық мағынасы: кез келген бастапқы - де интегралдық қисығына жақын берілген (1) жүйенің барлық интегралдық қисықтары 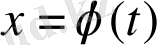(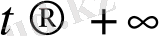) қисығына шексіз ұмтылатын болса, онда 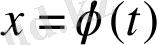асимптотикалық орнықты.
Анықтама 1.4. 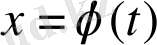шешімі Ляпунов бойынша орнықсыз деп аталады, егер кейбір 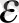мен және 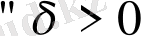үшін ең болмағанда бір 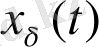шешімі және 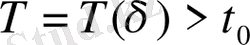мезеті табылып, келесі теңсіздіктер:

,

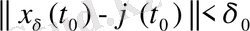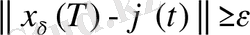
орындалатын болса.
Орнықсыздықтың геометриялық мағынасы: бастапқы мезетте 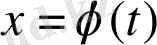интегралдық қисығына жақын орналасатын, кейінгі мезетте 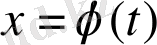қисығын айналдыра құрған мейлінше тар 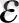-түтікшеден шығып кететін ең болмағанда бір интегралдық қисығы бар болса, 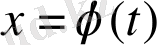шешімі орнықсыз.
Белгілі бір шешімнің орнықты, орнықсыздығын зерттеуді нөлдік шешімнің 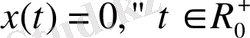орнықты, орнықсыздығын зерттеумен ауыстыруға болады.
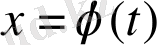орнықтылыққа зерттелінетін шешім болсын. Оның 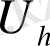аймағы

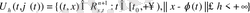
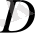-да жатсын, 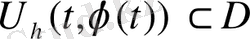. (1) жүйеге 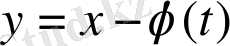ауыстыру енгізейік.
Сонда

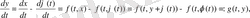
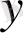жаңа функциясы бойынша келесі жүйені

(4)

аламыз. Мұнда

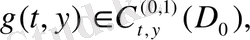
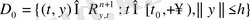және

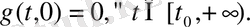
Сондықтан (4)-тің нөлдік шешімі 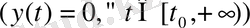бар және 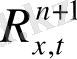кеңістігіндегі 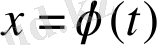шешіміне сәйкес. Осы берілген (4) жүйе келтірілген жүйе деп аталады. Берілген 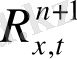кеңістігіндегі 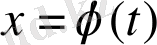шешімінің орнықтылығын зерттеу 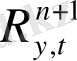кеңістігіндегі 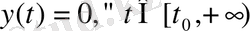шешімінің орнықтылығын зерттеуге әкеледі. Сондықтан анықтаманың жалпылығына келеміз, (1) жүйе (4) түрге келтірілген, яғни (1) жүйенің нөлдік шешімі бар 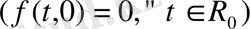. Онда келтірілген тұжырымдарды (1) жүйенің нөлдік шешімі үшін беру жеткілікті.
Анықтама 1.1*. (1) жүйенің нөлдік шешімі 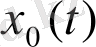орнықты деп аталады, егер 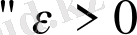және бастапқы 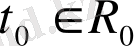мезеті үшін 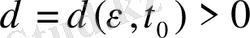саны табылып, 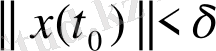теңсіздігін қанағаттандыратын (1) жүйенің 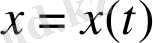шешімдері үшін келесі теңсіздік:

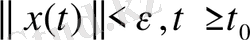
орындалатын болса.
Нөлдік шешімінің орнықтылығы геометриялық тұрғыдан 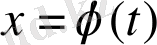шешімінің орнықтылығы сияқты, бірақ тек 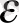- түтікше өсі 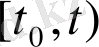сәулесі болатын цилиндр түрде болады.
Анықтама 1.2*. Егер 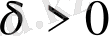санын 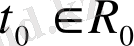-ден тәуелсіз, -нан тәуелді етіп алуға болса, нөлдік шешім бірқалыпты орнықты деп аталады.
Анықтама 1.3*. Нөлдік шешім орнықты және бастапқы мезеті үшін 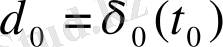табылып, теңсіздікті қанағаттандыратын барлық 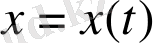шешімдері үшін 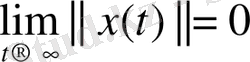теңдігі орындалса, нөлдік шешім асимптотикалық орнықты деп аталады. Геометриялық тұрғыдан қарасақ, бастапқы мезетте 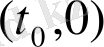нүктесіне аз қашықтықтағы интегралдық қисықтар кезде жарты өсіне шексіз ұмтылады.
Анықтама 1.4*. Нөлдік шешім орнықсыз деп аталады, егер нөлдік шешім орнықты болмаса, яғни кейбір мен 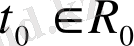бастапқы мезетінде және 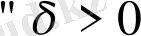үшін ең болмағанда 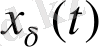шешімімен 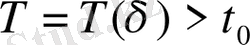мезеті табылып, мына теңсіздік:

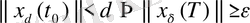
орындалатын болса.
Анықтама 1.5. 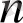өлшемді дифференциалдық жүйенің 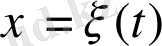шешімі

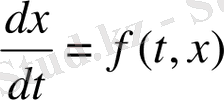
шартты орнықты [7] деп аталады, егер 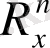бастапқы мәндердің 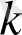-өлшемді теңсіздігін қанағаттандыратын 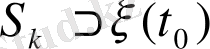жиын болып, мына шартқа бағынатын 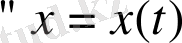шешімдері үшін

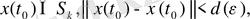
теңсіздігінің орындалуынан мына теңсіздік:

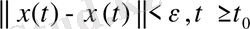
орындалатын болса.
Шартты орнықтылық асимптотикалық деп аталады, егер

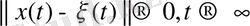
онда

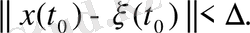
- кейбір оң тұрақтылар)

Мысал. Берілген теңдеудің және шартты қанағаттандыратын шешімнің орнықтылығын зерттеу.

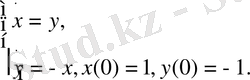
Коши түріндегі жалпы шешімі:

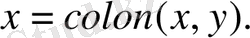
Мұнда
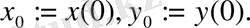
Шарттарды қанағаттандыратын шешім

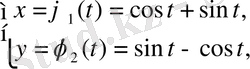
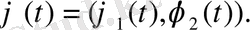
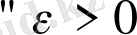үшін саны табылып,

Шешім орнықты және 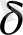саны 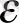-нан тәуелді болғандықтан, орнықтылық бірқалыпты. Ал 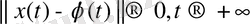болғандықтан, шешім асимптотикалық орнықты емес.

1.2 Бірінші жуықтау бойынша орнықтылық туралы Ляпунов теоремасы

Қалыпты жүйе қарастырайық:

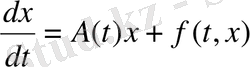(1)

мұндағы

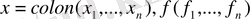
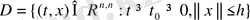
Енді 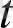өсінің кішкене аймағында шамасы аз 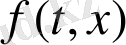вектор - функциясын ескермей, келесі жүйе қарастырайық:

(2)

Бұл жүйе (1) жүйенің бірінші жуықтау немесе сызықты жуықтау жүйесі деп аталады [11].
Кейде берілген сызықты емес (1) жүйенің нөлдік шешімінің орнықты, орнықсыздығын анықтау үшін тек сызықты (2) жүйені қарастыру жеткілікті болуы мүмкін. Мүмкіндік нәтижесінде алынған (1) жүйенің нөлдік шешімінің орнықты, орнықсыздығын бірінші жуықтау бойынша орнықтылық немесе орнықсыздық дейді.
(1) жүйенің дербес жағдайын қарастырайық:

(3)

мұнда 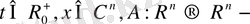тұрақты матрица,

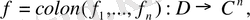
(4)

Мұндағы
Ляпунов теоремасы [1]. Егер берілген А матрицасының барлық меншікті мәндерінің нақты бөліктері теріс болса, (3) жүйенің нөлдік шешімі (4) теңсіздікті қанағаттандыратын 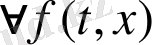функциясы үшін кезде бірқалыпты және асимптотикалық орнықты болады.
Егер А матрицасының ең болмағанда бір меншікті мәнінің нақты бөлігі оң болса, (3) жүйенің нөлдік шешімі (4) теңсіздікті қанағаттандыратын орнықсыз болады.
Дәледеуі. I бөлігінің дәлелдемесі [4]. 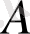матрицасын жордандық түрге келтіретін айрықша емес матрицаны 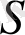арқылы, ал жордандық түрдегі әр ұяшыққа сәйкес келетін меншікті мәндерді 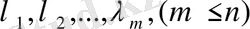арқылы белгілейміз.Ал меншікті мәндерге сәйкес келетін ұяшықтардың реті болсын. Ұяшықтардың өздерін сәйкес 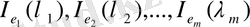арқылы белгілейік. Онда

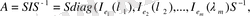
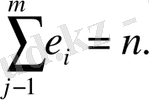
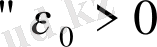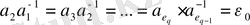үшін теңдіктерді қанағаттандыратын нөлге тең емес 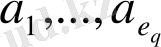сандарын алып, құрылған диагональ матрицаны қарастыралық:

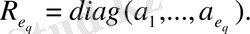(5)

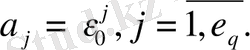деп алуға болады.Онда .
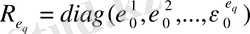(5) матрицаның көмегімен:

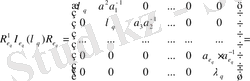
теңдік алынады.

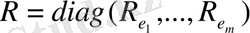
матрицасын қарастыралық. Сонда ұяшықтардан құрылған матрицаларды көбейту ережесіне сүйеніп келесі

теңдікті аламыз. Мұнда

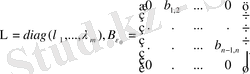
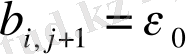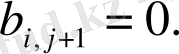
және немесе 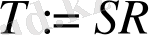деп белгілесек, (3) жүйеге ауыстыру енгізелік:

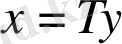(6)

Онда

.

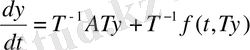Осы теңдіктегі

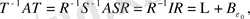
сондықтан

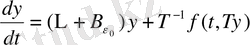,(7)

мұндағы

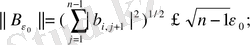
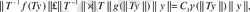
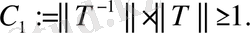
Теореманың шарты бойынша
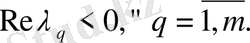
Сондықтан

деп белгілесек, болады. 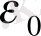саны келесі теңсіздікті

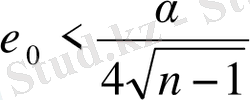
қанағаттандыратындай етіп алайық. Мұнда 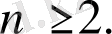Егер 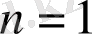болса, А матрицасы: 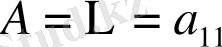. Онда
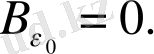
Келесі теңсіздіктің

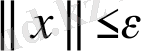(8)

орындалуынан

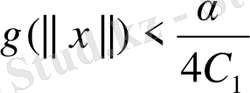(9)

берілген теңсіздік орындалатындай етіп 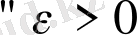санын және оған 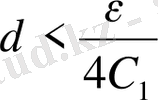орындалатындай етіп, 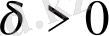санын таңдайық.
Бастапқы мәні теңсіздігін қанағаттандыратын (3) - тің шешімін қарастырайық. 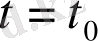мәнінде 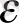-нан кіші болғандықтан, 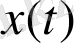үзіліссіз функциясы

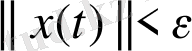(10)

теңсіздігін 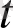- ның 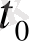- ге жақын мәндерінде қанағаттандырады. Енді 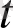- ның 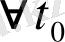- ден үлкен мәндерінде орындалатынын көрсетейік. Кері жориық. Берілген теңсіздік 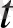-ның кейбір мәндерінде орындалмайды делік және сол теңсіздік орындалмайтын бірінші нүкте болсын. Онда

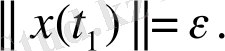(11)

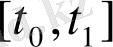-де келесі теңдікті қарастырайық:

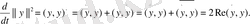
-де (8) орындалады:

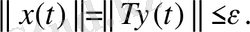
(9) теңсіздігіне сүйеніп келесі

теңсіздігін аламыз. (7) жүйеден келесідей теңдік алынады:

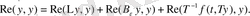
Ал

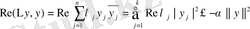
Сондықтан

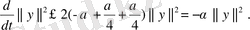
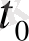-ден 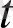- ға дейін интегралдап

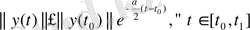
(6) - ны ескерсек

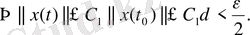(12)

Теңсіздік 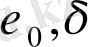сандарының таңдап алынған мәндерінде теңсіздігі орындалатын кесінді жоқ. Онда (11) орындалатын 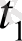мәні тіптен жоқ, яғни

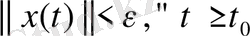(13)

(10) және (13) теңсіздіктердің орындалуы (3) жүйенің нөлдік шешімінің орнықтылығын білдіреді. саны тек санына тәуелді болғандықтан, орнықтылық бірқалыпты. (12) теңсіздіктен теңдігі алынатындықтан, нөлдік шешім асимптотикалық орнықты.
II бөлігінің дәлелденуі [2]. Енді

деп алайық. саны теңсіздігін қанағаттандырады. Дәлелдеуді жағдайында қарастырамыз, себебі болғанда дәлелдеу жеңіл.
саны табылып, берілген матрицасын диагональдық түрге келтіретін айрықша емес матрицаны арқылы белгілесек, яғни

Келесі теңсіздікті

қанағаттандыратын санын алып, (3) жүйеге ауыстыруын енгізейік. матрицасы мен вектор-функциясы комплекс мәнді.Сонда

(14)

және матрицасының нақты бөлігі нөлге тең болатындай меншікті мәні жоқ.
саны үшін саны табылып, мына

теңсіздіктері орындалады. Онда немесе болғанда,

теңсіздігі алынады. вектор функциясының координаттарын , яғни арқылы, ал келесі айырманы

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.