Функция шегінің анықтамасы бойынша теңдік мына теңсіздіктермен парапар

Петропавл, 2021

Петропавл, 2021

АҢДАТПА

Дипломдық жұмыста жоғары сынып оқушыларына арналған «Шек және үздіксіздік» тақырыбында оқушыларды оқыту әдістемесі қарастырылады. Функцияның шегін есептеу және функцияны үздіксіздікке зерттеу шешімдері бар мысалдар келтірілген. Сонымен қатар, БЖБ және ТЖБ тапсырмалары әзірленді.

АННОТАЦИЯ

В дипломной работе рассматривается методика обучения учащихся теме «Предел и непрерывность» для учащихся старшего звена. Приведены примеры с решениями на вычисление предела функции и исследование функции на непрерывность. Кроме того, разработаны задания на СОР и СОЧ.

ANNOTATION

The thesis discusses the methodology of teaching students the topic «Limit and continuity» for senior students. Examples with solutions for calculating the limit of a function and investigating the continuity of a function are given. In addition, tasks for SOR and SOC have been developed.

МАЗМҰНЫ

КІРІСПЕ5

1. ФУНКЦИЯНЫҢ НҮКТЕДЕГІ ШЕГІ8

1. 1 Шектер туралы негізгі теоремалар8

1. 2 Бірінші тамаша шек. 9

1. 3. Шектердің қасиеттері:9

2. ҮЗДІКСІЗДІК ФУНКЦИЯСЫ20

2. 1. Үздіксіз функциясының қасиеттері:20

2. 2 Интервалдағы функцияның үздіксіздігі. 30

2. 3. Экономикада шек және үздіксіздікті қолдану. 34

2. 4. Шек тақырыбына шешімдермен мысалдар37

2. 5. Үздіксіздік тақырыбына шешімдермен мысалдар. 39

2. 6. Тақырып бойынша сабақтың қысқаша мазмұны. 43

2. 7. БЖБ және ТЖБ53

ҚОРЫТЫНДЫ59

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ60

КІРІСПЕ

Математика курсының негізгі мақсаты студенттердің теориялық білім мен практикалық дағдыларды игеруі болып табылады, бұл студенттерді жоғары оқу орындарында кәсіптік білім алуға және білімін жалғастыруға қажетті математикалық білім мен дағдылармен қамтамасыз етуге мүмкіндік береді. Математиканы оқыту міндетіне мыналар кіреді:

- арнайы пәндерді оқу үшін қажетті нақты математикалық білімді игеру; - қоғамда толыққанды жұмыс істеуге тән ойлау сапасын қалыптастыру;

- математиканың идеялары мен әдістері туралы түсінік қалыптастыру;

- жалпы адамзаттық мәдениеттің бір бөлігі ретінде математика туралы түсінік қалыптастыру.

«Математика» пәнін зерделеудің мақсаты білім алу және техникалық жоғары оқу орындарында зерделенетін негізгі ұғымдарды, заңдарды, формулаларды, теоремаларды және математикалық зерттеу әдістерін меңгеру болып табылады. Математикада математикалық объектілерге - функцияға, функционалға, операторға, геометриялық бейнелерге, векторларға, матрицаларға теориялық-жиындық көзқарастар бар.

Жоғары математиканың негізі математикалық талдау болып табылады. Нақты жағдайларда жүретін динамикалық процестерді түсіндіру және мәнін түсіну үшін, оларға осы салада қойылған шеттік есептерді шығару үшін қатаң математикалық талдау жүргізу қажет.

Оқушының пәнді зерделеу нәтижесінде:

• негізгі ұғымдар, анықтамалар, формулалар, теоремалар және аталған бөлімдердің есептерін шығару әдістері туралы түсінігі болуы тиіс;
• жоғары математика курсын берілген типтік оқу бағдарламасы көлемінде білуі тиіс;
• қолданбалы есептерді шығару үшін қазіргі заманғы математикалық әдістерді қолдана білу ептілігі болуы тиіс;
• математикалық ойлау мен логиканы дамыту, жалпы теориялық және арнайы техникалық пәндерді табысты зерделеу үшін іргелі ғылымның жетістіктерін пайдалану дағдыларын иеленуі тиіс;
• нақты техникалық есептерді шығару үшін математикалық модельдеу әдістерін таңдау кезінде құзыретті болуы тиіс.

Математика ғылымы барлық ғылымдардың арасында ерекше орын алады. Математика өзінен басқа ілімдер үшін сан және белгі түрінде табиғаттың әртүрлі құбылыстарының ара қатынастарын өрнектейтін тіл болып саналады. Сондықтан «ғылым өзінің шыңына математиканың көмегінсіз жетуі мүмкін емес» деп бекерге айтылмаған. Мұғалімнің міндеті - бірінші сабақтан бастап оқушыларды осы пәнді жақсы көруге және түсінуге үйрету. Математика пәнінде баланың оқу процесінде ойлау қабілетін дамытуға үлкен мүмкіндік бар.

Дипломдық жұмыс өзектілігі: Шек және үздіксіздік тақырыбына байланысты материалдар мектептегі математика курсының маңызды бөлігін құрайды. Тақырыпты ашу үшін біз функцияның нүктедегі шегінің аталған анықтамасына сүйенеміз. Функцияның шегін негізгі ұғым ретінде қарастырамыз. Оқушыларды функцияның шегі ұғымы мен функцияның үздіксіздігі ұғымын үйренуге дайындау үшін, осы тақырыпты зерттегенде қандай ұғымдарға тап болатынын талдау керек.

Дипломдық жұмыстың мақсаты:

Математикалық әдістер ғылым, техника, экономика және басқару мәселелерін шешуде үлкен роль атқарады. Сондықтан математиканы оқытудың алдына келесі мақсаттар қойылады:

- оқушылардың математикалық және алгоритмдік ойлауын дамыту;

- оқушылардың математикалық есептерді зерттеу және оларды шешу әдістерін игеру;

- оқушылардың қолданбалы кәсіптік есептерді шешуде математикалық білімдерін қолдану дағдыларын қалыптастыру.

Дипломдық жұмыс міндеті:

1. Оқу-әдістемелік әдебиеттерді зерттеу;

2. Тақырып бойынша негізгі терминдерді қарастыру;

3. Шешімнің негізгі әдістері мен тәсілдерін көрсету;

4. Әдебиетте табылған фактілерді қорытындылау және жүйелеу;

5. Оқушылар үшін ерекше әдіспен шешілетін бірқатар тапсырмалар жасау.

Зерттеу объектісі жалпы білім беретін мектеп оқушыларын «Шек және үздіксіздік» тақырыбы бойынша оқыту процесі болып табылады.

Зерттеу пәні алгебра және анализ бастамаларын оқыту барысында математикалық анализдің негізгі ұғымдарын есептерді пайдалану арқылы қалыптастыру.

Теориялық маңыздылығы: зерттеу барысында негізгі мектеп алгебрасы курсында «Шек және үздіксіздік» тақырыбын оқытудың әдістемелік ерекшеліктері анықталады.

Практикалық маңыздылығы негізгі мектеп оқушыларының «Шек және үздіксіздік» тақырыбын оқыту бойынша әдістемелік ұсыныстарды және алгебраның мектеп курсында және оқытудың педагогикалық бағыттарындағы мұғалімдерге осы тақырыпты оқытуда қолдануға болатын әдіс-тәсілдерді көрсету.

Зерттеу әдістері: мектеп бағдарламаларын, оқу әдебиеттері мен әдістемелік құралдарды зерттеу және талдау, мысалдар ұсыну.

Жұмыстың құрылымы:

Дипломдық жұмыс 63 (алпыс үш) беттен, кіріспеден, екі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.

Кіріспеде мақсаттар мен міндетттер және атқарылатын жұмыстың қысқаша сипаттамасы анықталған.

Бірінші бөлімде жалпы шек және үздіксіздік ұғымы, олардың анықтамасы, қасиеттері және дәлелдемелері көрсетілген.

Екінші бөлімде шек және үздіксіздіктің қолданылуы және есептеу мысалдары ұсынылған.

Қорытындыда жүргізілген зерттеудің негізгі нәтижелері мен қорытындылары ұсынылған.

1. ФУНКЦИЯНЫҢ НҮКТЕДЕГІ ШЕГІ

1. 1 Шектер туралы негізгі теоремалар

y=f(x) функциясы ${\ x}_{0}\$ ${\ x}_{0}\$ нүктесінің қандай да бір маңайында (x нүктесінің өзі кірмеуі мүмкін) анықталсын.

Функция нүктедегі шегінің екі өзара эквивалентті анықтамасын тұжырымдайық.

Анықтама 1. («тізбектер» тілінде немесе Гейне бойынша) . Егер x-ге жинақталатын $x_{n}$ $x_{n}$ , n $\in$ $\in$ N аргументінің мүмкін мәндерінің кез-келген тізбегі А санына жинақталса, А саны y=f(x) функциясының шегі деп аталады. Бұл жағдайда $\lim_{x \rightarrow x_{0}}{f(x) = A}$ $\lim_{x \rightarrow x_{0}}{f(x) = A}$ немесе $x \rightarrow x_{0}$ $x \rightarrow x_{0}$ болғанда $f(x) \rightarrow A$ $f(x) \rightarrow A$ деп жазады. $\lim_{x \rightarrow x_{0}}{f(x) = A}$ $\lim_{x \rightarrow x_{0}}{f(x) = A}$ функциясы шегінің геометриялық мағынасы: $x_{0}$ $x_{0}$ нүктесіне жеткілікті жақын барлық x нүктесі үшін функцияның сәйкес мәндері A санынан аз ғана айырмашылығы болады.

Бір жақты шектер

$\lim_{x \rightarrow x_{0}}{f(x) = A}$ $\lim_{x \rightarrow x_{0}}{f(x) = A}$ функция шегінің анықтамасы бойынша x нүктесі $x_{0}$ $x_{0}$ -ге кез-келген жағдайда ұмтылады: $x_{0} -$ $x_{0} -$ ден кіші болса да, $x_{0} -$ $x_{0} -$ ден үлкен болса да немесе $x_{0}$ $x_{0}$ нүктесінің аймағында ауытқыса да.

Кейде x аргументінің $x_{0}$ $x_{0}$ -ге жақындауының тәсілі функция шегінің мәніне айтарлықтай әсер ететін жағдайлар болады. Сондықтан, бір жақты шектер ұғымы енгізіледі.

Егер кез-келген $\varepsilon > 0$ $\varepsilon > 0$ үшін $\delta = \delta(\varepsilon) > 0$ $\delta = \delta(\varepsilon) > 0$ саны табылып, $x \in (x_{0} - \delta; x_{0})$ $x \in (x_{0} - \delta; x_{0})$ болғанда $\left f(x) - A_{1} \right < \varepsilon$ $\left f(x) - A_{1} \right < \varepsilon$ теңсіздігін орындалса, $A_{1}$ $A_{1}$ саны y=f(x) функциясының сол жақ шегі деп аталады. Сол жақ шекті $\lim_{x \rightarrow x_{0}}{f(x) = A_{1}}$ $\lim_{x \rightarrow x_{0}}{f(x) = A_{1}}$ деп немесе қысқаша, f( $x_{0} - 0) = A_{1}$ $x_{0} - 0) = A_{1}$ деп жазады. Осылайша, функцияның оң жақты шегі анықталып, қысқаша төмендегідей жазылады:

Оң жақты шекті қысқаша $f\left( x_{0} + 0 \right) = A_{2}$ $f\left( x_{0} + 0 \right) = A_{2}$ деп белгілейді. Функцияның оң жақты және сол жақты шектері бір жақты шектер деп аталады. Егер $\ \lim_{x \rightarrow x_{0}}{f(x) = A}$ $\ \lim_{x \rightarrow x_{0}}{f(x) = A}$ бар болса, онда екі бір жақты шектер бар болады және A= $A_{1} = A_{2}$ $A_{1} = A_{2}$ . Кері тұжырым да орынды: егер екі бір жақты шектер бар болса және олар тең болса, онда $A = \lim_{x \rightarrow x_{0}}{f(x) }$ $A = \lim_{x \rightarrow x_{0}}{f(x) }$ және 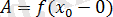шегі бар болады. Егер $A_{1} \neq A_{2}$ $A_{1} \neq A_{2}$ болса, онда $\lim_{x \rightarrow x_{0}}{f(x) }$ $\lim_{x \rightarrow x_{0}}{f(x) }$ шегі жоқ.

Теорема. Екі функцияның шектерінің қосындысы (айырмасы) олардың шектерінің қосындысына (айырмасына) тең:

$\lim_{x \rightarrow x_{0}}{\left( f(x) \pm \varphi(x) \right) = \lim_{x \rightarrow x_{0}}{f(x) \pm \lim_{x \rightarrow x_{0}}{\varphi(x) }}}$

Теорема. Екі функцияның көбейтіндісінің шегі олардың шектерінің көбейтіндісіне тең:

$\lim_{x \rightarrow x_{0}}{\left( f(x) \bullet \varphi(x) \right) = \lim_{x \rightarrow x_{0}}{f(x) \bullet \lim_{x \rightarrow x_{0}}{\varphi(x) }}}$

Салдар. Тұрақты көбейтіндіні шек таңбасының алдына шығаруға болады

$\lim_{x \rightarrow x_{0}}{c \bullet f(x) = c\lim_{x \rightarrow x_{0}}{f(x) }}$

Теорема. Егер бөлшектің бөлімінің шегі 0-ден өзгеше болса, бөлшектің шегі бөлшек алымының шегінің бөлімінің шегіне бөліндісіне тең:

$\underset{x \rightarrow x_{0}}{\ \ \ \ \ \ \ \ \ \ \ lim}\frac{f(x) }{\varphi(x) } = \frac{\lim_{x \rightarrow x_{0}}{f(x) }}{\lim_{x \rightarrow x_{0}}{\varphi(x) }}$ $\underset{x \rightarrow x_{0}}{\ \ \ \ \ \ \ \ \ \ \ lim}\frac{f(x) }{\varphi(x) } = \frac{\lim_{x \rightarrow x_{0}}{f(x) }}{\lim_{x \rightarrow x_{0}}{\varphi(x) }}$ , $\left( \lim_{x \rightarrow x_{0}}{\varphi(x) \neq 0} \right)$ $\left( \lim_{x \rightarrow x_{0}}{\varphi(x) \neq 0} \right)$

1. 2 Бірінші тамаша шек.

Көп жағдайда өрнегі тригонометриялық функциядан құралған шекті есептегенде, бірінші тамаша шек деп аталатын

$\lim_{x \rightarrow 0}\frac{\sin x}{x} = 1$

шегі қолданылады. Бұл шек былай оқылады: аргументі нөлге ұмтылғандағы синустың аргументіне қатынасының шегі бірге тең.

Екінші тамаша шек

$x_{n} = \left( 1 + \frac{1}{n} \right) ^{n}$ $x_{n} = \left( 1 + \frac{1}{n} \right) ^{n}$ , n $\in N$ $\in N$

сандық тізбегінің шегі е санына тең :

$\underset{x \rightarrow \infty}{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ lim}\left( 1 + \frac{1}{n} \right) ^{n}$ $\underset{x \rightarrow \infty}{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ lim}\left( 1 + \frac{1}{n} \right) ^{n}$ =e

1. 3. Шектердің қасиеттері:

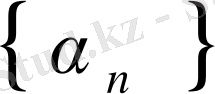Анықтама. Егер болса, онда тізбек шексіз аз тізбек деп аталады.

Осы анықтамадан және тізбек шегінің анықтамаларынан тікелей мынадай қорытындыға келеміз, егер 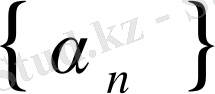шексіз аз тізбек болса, онда алдын ала берілген саны үшін табылып, барлық үшін теңсіздігі орындалады.

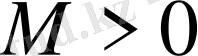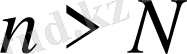Анықтама. Егер кез - келген саны үшін саны табылып, барлық үшін 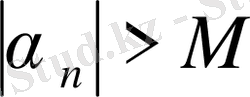теңсіздігі орындалса, онда тізбегі шексіз үлкен тізбек деп аталады.

Егер шексіз үлкен тізбектің мүшесі болса, онда тізбек ке (- 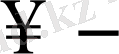ке) ұмтылады дейміз және оны былай белгіленеді:

( )

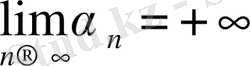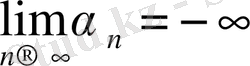Жалпы оны былай да белгіленеді

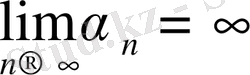
Егер шексіз аз бен шексіз үлкен тізбектердің арасындағы байланысты қарастырайық.

Теорема 1. 1. Егер 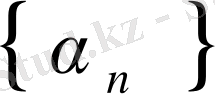Equation. 3 шексіз аз тізбек болса және 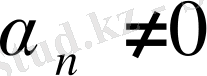Equation. 3 болса, онда 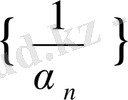Equation. 3 - шексіз үлкен тізбек болады және керісінше, егер 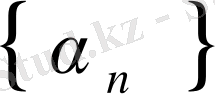Equation. 3 шексіз үлкен тізбек болса, онда Equation. 3 -шексіз аз тізбек болады.

Теорема 1. 2. Шексіз аз екі тізбектің алгебралық қосындысы да шексіз аз тізбек, яғни Equation. 3

Теорема 1. 3. Шексіз аз тізбек шектелген.

Теорема 1. 4. Шектелген тізбек пен шексіз аз тізбектердің көбейтіндісі шексіз аз тізбек болады.

Теорема 1. 5. Шексіз аз екі тізбектің көбейтіндісі де шексіз аз тізбек болады.

Теорема 1. 6. Equation. 3 саны {х _n } тізбегінің шегі болуы үшін мына 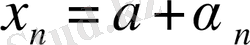Equation. 3 теңдігінің орындалуы қажетті әрі жеткілікті, мұндағы Equation. 3 шексіз аз тізбек.

Теорема 1. 7. Жинақты {х _n } мен {у _n } тізбектерінің алгебралық қосындысы да жинақты тізбек, ал оның шегі {х _n } мен {у _n } тізбектері шектерінің алгебралық қосындысына тең: 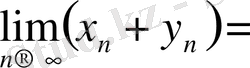Equation. 3 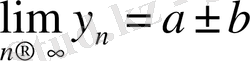Equation. 3

Ескерту. Егер 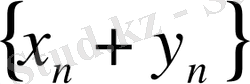Equation. 3 жинақты тізбек болса, онда {х _n } мен {у _n } тізбектерінің жинақтылығы жайлы ештеңе айтуға болмайды.

Теорема 1. 8. Жинақты {х _n } мен {у _n } тізбектерінің көбейтіндісіне де жинақты тізбек, ал оның шегі {х _n } мен {у _n } тізбектері шектерінің көбейтіндісіне тең:

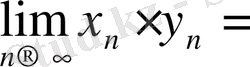
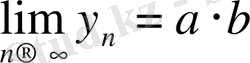
Осы теоремадан мынадай салдар аламыз.

Салдар 1. Егер Equation. 3 болса, Equation. 3 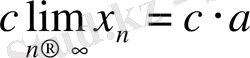онда мұндағы с- тұрақты сан.

Салдар 2. Егер 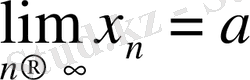Equation. 3 болса, онда 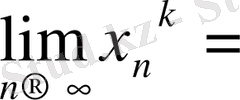Equation. 3

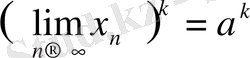
Теорема 1. 9. Егер {хn} тізбектің шегі 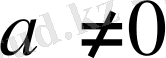Equation. 3 болса, онда 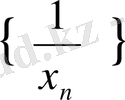Equation. 3 тізбегі шектелген.

Теорема 1. 10. Жинақты {х _n } мен {y _n } тізбектерінің қатынасы да жинақты тізбек, ал оның шегі {х _n } мен {y _n } тізбектер шектерінің қатынасына тең:

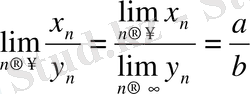Equation. 3, мұндағы 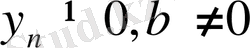Equation. 3

Теорема 1. 11. Егер {хn} жинақты тізбегінің белгілі бір номерінен бастап барлық мүшесі үшін 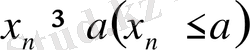Equation. 3 теңсіздігі орындалса, онда 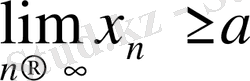Equation. 3 ( 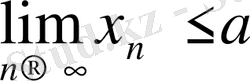Equation. 3 ) болады.

Осы теоремадан мынадай салдар аламыз.

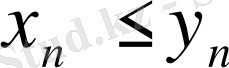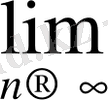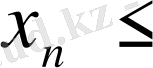
Салдар 1. Егер жинақты {х _n } мен {y _n } тізбектерінің белгілі бір номерінен бастап барлық мүшесі үшін Equation. 3 теңсіздігі орындалса, онда Equation. 3 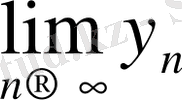теңсіздігі де орындалады.

Теорема 1. 12. Жинақты {х _n }, {y _n } және {z _n } тізбектерінің белгілі бір номерінен бастап барлық мүшесі үшін 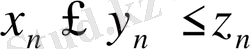Equation. 3 теңсіздігі орындалсын. Егер а саны {х _n } мен {z _n } тізбектерінің шегі болса, онда ол {y _n } тізбегінің де шегі болады.

Анықтама. {х _n } тізбек кемімейтін (өспелі) тізбек деп аталады, егер кез - келген n үшін 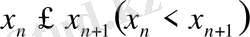Equation. 3 теңсіздік орындалса, ал егер 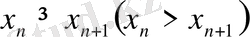Equation. 3 теңсіздігі орындалса, онда ол өспейтін (кемімелі) тізбек деп аталады.

Анықтамада аталған тізбектерді монотонды тізбектер дейміз. Осы анықтамадан, монотонды тізбек не жоғарыдан не төменнен шектелген. Мысалы, өспейтін тізбек жоғарыдан, ал кемімейтін тізбек төменнен шектелген. Шынында да, кез - келген n үшін өспейтін {х _n } тізбегінде 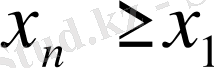Equation. 3 теңсіздігі, ал кемімейтін {y _n } тізбегіне 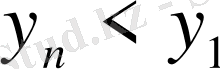Equation. 3 теңсіздігі орындалады, яғни осы тізбектердің әр қайсысында бірінші мүшесімен шектелген. Сонымен, егер монотонды тізбек екі жақтан да, яғни әрі төменнен, әрі жоғарыдан шектелсе, онда ол шектелген, яғни оның шегі бар. Монотонды тізбекке тән осы қасиет монотонды емес тізбекке орындалмайды, яғни монотонды емес тізбектің шегі жоқ. Мысалы, Equation. 3 тізбегі монотонды емес, әрі оның шегі жоқ.

Теореме 1. 13. Монотонды шектелген тізбектің шегі бар.

Осы теорема мұндай тұжырым аламыз: монотонды шектелген тізбек жинақты; монотонды жинақты тізбек шектелген.

Сонымен, монотонды тізбекке қойылған шектелгендік шарт осы тізбектің жинақты болуы үшін қажетті әрі жеткілікті.

Математика, механика, физика, радиотехника және радиохимия салаларында e санының атқаратын қызметі айырықша. Енді осы санын анықтайық.

Жалпы мүшесі Equation. 3 болатын тізбек қарастырайық осы тізбектің өспелі және де жоғарыдан шектелгендігін дәлелдейік. Алдымен, өспелі тізбек екенін дәлелделік. Олу үшін x _n -ді Ньютон биномы бойынша жіктеп және өрнектейік:

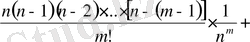
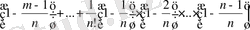(1. 5)

Осы тізбектің хn мен -ші мүшелерін сәйкес қосылғыштарын салыстырайық. Сонда, -ші мүшенің әрбір қосылғышы хn мүшедегі сәйкес қосылғышынан үлкен жәнеде -ші оң бір қосылғыш артық, ол .

Сонымен, әрбір n бүтін оң сан үшін х _n > теңсіздігі орындалады, яғни {х _n } - өспелі тізбек.

... жалғасы

Функция шектері туралы теоремалар

Бірінші тамаша шек

Ақырсыз кішкене және ақырсыз үлкен функциялар

Тізбектің шегінің анықтамасы

Рационал сандар жиынының қасиеттері

Шектер теориясы түсінігі

Шектер теориясы жайлы

Функцияның шексіздіктегі шегі

Шектер теориясы туралы

Тізбектің шегі туралы теоремалар

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс