Математика 3: Өріс теориясы, дифференциалдық теңдеулер, қатарлар, комплекс айнымалылар және ықтималдық теориясы - дәрістер жинағы


АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС ИНСТИТУТЫ
Жоғары математика кафедрасы
Математика 3
Барлық мамандықтардың
барлық оқу түрінің студенттеріне арналған
дәрістер жинағы
Алматы 2008
ҚҰРАСТЫРУШЫЛАР: Жұматаева С. А., Темешева С. М. Математика 3. Барлық мамандықтардың барлық оқу түрінің студенттеріне арналған дәрістер жинағы. - Алматы: АЭжБИ, 2008. - 67 б.
Ұсынылып отырған дәрістер жинағына жоғары математика курсының “Математика 3” бөліміне енгізілген 17 дәрісі (“Өріс теориясы”, “Дифференциалдық теңдеулер”, “Қатарлар”, “Комплекс айнымалыдан тәуелді функция және амалдық есептеу”, “Ықтималдықтар теориясының элементтері” тараулары бойынша) кірген. Дәрістер жинағы Алматы энергетика және байланыс институтының барлық мамандықтарының барлық оқу түрінің бакалаврларын оқытудың оқу жоспарына сәйкес келеді.
Мазмұны
Дифференциалдық теңдеулер.
Жай дифференциалдық теңдеулер . . . . . .
9
13
17
21
25
33
37
51
Кіріспе сөз
Ұсынылып отырған жинақта жоғары математика курсының “ Математика 3” бөліміне енгізілген 17 дәрісі кірген. Дәрістер жинағы Алматы энергетика және байланыс институтының барлық мамандықтарының барлық оқыту түрінің бакалаврларын оқытудың оқу жоспарына сәйкес келеді.
Дәрістер жинағы оқытушылар мен студенттерге пайдалы және жоғары математика курсының “Өріс теориясы”, “Дифференциалдық теңдеу-лер”, “Қатарлар”, “Комплекс айнымалыдан тәуелді функция және амалдық есептеу”, “Ықтималдықтар теориясының элементтері” тараулары бойынша аудиториялық сабақтар кезінде өзіндік жұмыстар өткізуге арналған.
Анықтамалар, теоремалар, формулалар нөмірлері екі саннан тұрады: олардың біріншісі дәріс нөмірін, ал екіншісі осы дәріс ішіндегі анықтаманың, теореманың, формуланың нөмірін білдіреді.
Оқу құралындағы материалды игеру студенттерге жоғары математика курсының аталып өткен тараулары бойынша жеткілікті жақсы білім алуға мүмкіндік береді.
№ 1 дәріс Өріс теориясы
Мазмұны: Өріс анықтамасы, өрістер теориясының элементтері. Векторлық өрістердің түрлері. Векторлық өрістің ағыны мен циркуляциясын есептеу. Остроградский-Гаусс теоремасы. Стокс теоремасы.
Дәрістің мақсаты: Векторлық сызықтар жиынтығын анықтайтын диффе-ренциалдық теңдеулер жүйесін құра білу, векторлық өрістің дивергенциясы мен роторын табу. Векторлық өрістің ағынын есептеуге Остроградский-Гаусс және Стокс теоремаларын қолдана білу.
1. 1 анықтама
 облысының әрбір
облысының әрбір
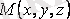 нүктесінде
нүктесінде
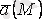 векторы анықталса,
векторы анықталса,
 облысында векторлық өріс берілді дейміз, басқаша айтқанда, векторлық өріс берілген болып есептеледі, егер әрбір
облысында векторлық өріс берілді дейміз, басқаша айтқанда, векторлық өріс берілген болып есептеледі, егер әрбір
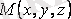 нүктесінде сәйкесінше
нүктесінде сәйкесінше
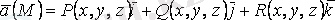 векторы берілсе векторлық өріс берілді дейміз (бұл жерде
векторы берілсе векторлық өріс берілді дейміз (бұл жерде
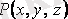 ,
,
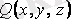 ,
,
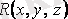 функциялары өздерінің дербес туындыларымен бірге үзіліссіз деп ұйғарамыз) .
функциялары өздерінің дербес туындыларымен бірге үзіліссіз деп ұйғарамыз) .
Векторлық өрістердің дербес жағдайлары
1. Егер
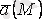 тұрақты вектор болса, яғни
тұрақты вектор болса, яғни
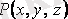 ,
,
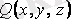 ,
,
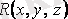 функциялары тұрақты болса, онда векторлық өріс біртекті болады.
функциялары тұрақты болса, онда векторлық өріс біртекті болады.
2
.
Егер
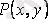 ,
,
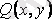 ,
,
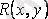 функциялары таңдап алынған координаттар жүйесінде екі айнымалыдан тәуелді функциялар және вектордың проекцияларының біреуі 0-ге тең болса, онда векторлық өріс жазық болады. Мысалы,
функциялары таңдап алынған координаттар жүйесінде екі айнымалыдан тәуелді функциялар және вектордың проекцияларының біреуі 0-ге тең болса, онда векторлық өріс жазық болады. Мысалы,
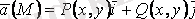 - жазық векторлық өріс.
- жазық векторлық өріс.
3. Егер
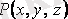 ,
,
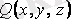 ,
,
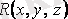 функциялары
функциялары
 -дан тәуелсіз болса, онда өріс стационарлық болады.
-дан тәуелсіз болса, онда өріс стационарлық болады.
1. 2 анықтама Векторлық өрістің векторлық сызығы деп әрбір нүктесіндегі жанамасының бағыты осы нүктеге сәйкес келетін вектор бағытымен беттесетін сызықты айтады.
Айталық,
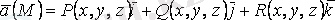 векторлық өрісі берілсін. Векторлық сызық параметрлік түрде берілсін:
векторлық өрісі берілсін. Векторлық сызық параметрлік түрде берілсін:
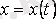 ,
,
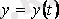 ,
,
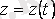 . Векторлық сызыққа
. Векторлық сызыққа
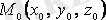 нүктесіндегі бағыттауыш векторы
нүктесіндегі бағыттауыш векторы
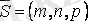 болатын жанамасы
болатын жанамасы
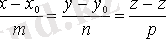 теңдеуімен беріледі. 1. 2 анықтамасы бойынша
теңдеуімен беріледі. 1. 2 анықтамасы бойынша
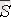 және
және
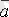 векторлары коллинеар болады, сондықтан, векторлардың коллинеар болу шартынан,
векторлары коллинеар болады, сондықтан, векторлардың коллинеар болу шартынан,
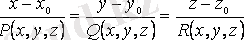 теңдеулерін аламыз.
теңдеулерін аламыз.
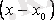 шамасы
шамасы
 аргументінің өсімшесі болғандықтан,
аргументінің өсімшесі болғандықтан,
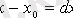 теңдігін аламыз. Осыған ұқсас
теңдігін аламыз. Осыған ұқсас
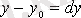 және
және
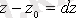 болады.
болады.
Сонымен,
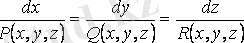 . (1. 1)
. (1. 1)
(1. 1) дифференциалдық теңдеулер жүйесі
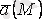 векторлық өрісінің векторлық сызықтар жиынтығын анықтайды.
векторлық өрісінің векторлық сызықтар жиынтығын анықтайды.
Вектордың ағыны
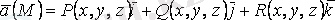 векторлық өрісі берілсін. Осы өрісте кейбір
векторлық өрісі берілсін. Осы өрісте кейбір
 бетін алып, оның бір жағына тоқталайық.
бетін алып, оның бір жағына тоқталайық.
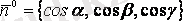 беттің осы жағының кез келген нүктесіндегі бірлік нормаль векторы болсын.
беттің осы жағының кез келген нүктесіндегі бірлік нормаль векторы болсын.
1. 3
анықтама
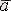 векторының
векторының
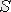 беті арқылы ағыны деп өріс векторы мен беттің бірлік нормаль векторының скаляр көбейтіндісінің
беті арқылы ағыны деп өріс векторы мен беттің бірлік нормаль векторының скаляр көбейтіндісінің
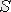 беті бойынша интегралы аталады. Оны төмендегідей белгілейді
беті бойынша интегралы аталады. Оны төмендегідей белгілейді
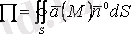 (1. 2)
(1. 2)
немесе
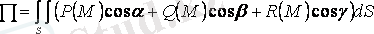
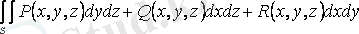 . (1. 3)
. (1. 3)
Дивергенция
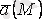 векторлық өрісінің еркін
векторлық өрісінің еркін
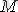 нүктесін қарастырамыз, оны толығымен өріске тиісті тұйық
нүктесін қарастырамыз, оны толығымен өріске тиісті тұйық
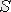 бетімен қоршаймыз.
бетімен қоршаймыз.
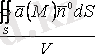 шамасын қарастырайық. Сұйықтың жылдамдықтар өрісінде бұл шама
шамасын қарастырайық. Сұйықтың жылдамдықтар өрісінде бұл шама
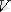 облысындағы уақыттың бірлігіндегі көлем бірлігіне қатысты пайда болатын сұйық мөлшерін анықтайды, яғни жанар көзінің орташа көлемдік қуатын анықтайды. Егер ағын 0-ден кіші болса, онда ағын көзінің қуаты туралы айтады.
облысындағы уақыттың бірлігіндегі көлем бірлігіне қатысты пайда болатын сұйық мөлшерін анықтайды, яғни жанар көзінің орташа көлемдік қуатын анықтайды. Егер ағын 0-ден кіші болса, онда ағын көзінің қуаты туралы айтады.
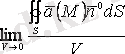 шегін есептейміз, анығырақ айтқанда
шегін есептейміз, анығырақ айтқанда
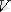 облысы
облысы
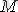 нүктесіне дейін сығылған жағдайдағы шекті есептейміз. Егер шек 0-ден артық болса, онда
нүктесіне дейін сығылған жағдайдағы шекті есептейміз. Егер шек 0-ден артық болса, онда
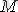 нүктесі жанар көзі, ал егер 0-ден кіші болса, онда
нүктесі жанар көзі, ал егер 0-ден кіші болса, онда
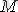 ағын көзі болады. Шектің көзі жанар көзінің қуатын немесе ағын көзінің қуатын сипаттайды.
ағын көзі болады. Шектің көзі жанар көзінің қуатын немесе ағын көзінің қуатын сипаттайды.
1. 4 анықтама
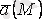 векторлық өрісінің дивергенциясы немесе жинақсыздығы деп
векторлық өрісінің дивергенциясы немесе жинақсыздығы деп
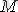 нүктесін қоршайтын бет арқылы
нүктесін қоршайтын бет арқылы
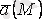 векторының ағынының сол бетпен қоршалған дене көлеміне қатынасын (аталмыш бет
векторының ағынының сол бетпен қоршалған дене көлеміне қатынасын (аталмыш бет
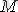 нүктесіне сығылған жағдайдағы) шегін айтады да, төмендегідей белгілейді
нүктесіне сығылған жағдайдағы) шегін айтады да, төмендегідей белгілейді
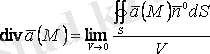 . (1. 4)
. (1. 4)
Теорема.
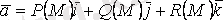 векторлық өрісінің
векторлық өрісінің
 нүктесіндегі дивергенциясы
нүктесіндегі дивергенциясы
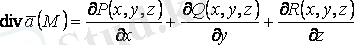 (1. 5)
(1. 5)
формуласы бойынша табылады.
Остроградский-Гаусс теоремасы. Тұйық беттің ішінен шығатын вектордың ағыны өрістің дивергенциясынан осы бетпен қоршалған дене көлемі бойынша алынған үш еселі интегралға тең
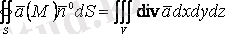
немесе
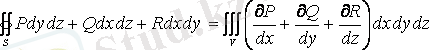 . (1. 6)
. (1. 6)
Дивергенция қасиеттері
1.
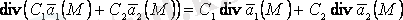 ;
;
2.
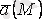 - векторлық өріс, ал
- векторлық өріс, ал
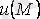 - скалярлық өріс болсын, онда
- скалярлық өріс болсын, онда
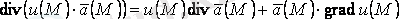 .
.
Векторлық өрістің циркуляциясы
1. 5
анықтама
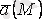 векторының
векторының
 тұйық контуры бойынша циркуляциясы деп
тұйық контуры бойынша циркуляциясы деп
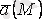 векторы мен осы контурды жанап өтетін
векторы мен осы контурды жанап өтетін
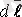 векторының скалярлық көбейтіндісінің
векторының скалярлық көбейтіндісінің
 контуры бойынша қисық сызықты интегралы аталады
контуры бойынша қисық сызықты интегралы аталады
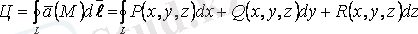 . (1. 7)
. (1. 7)
Векторлық өрістің роторы
1. 6 анықтама
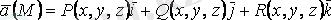 векторлық өрісінің роторы (құйыны) деп
векторлық өрісінің роторы (құйыны) деп
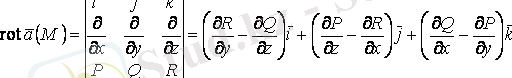 (1. 8)
(1. 8)
векторы аталады.
Стокс теоремасы.
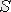 беті арқылы
беті арқылы
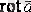 -ның ағыны
-ның ағыны
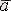 векторының
векторының
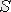 -тің шекарасы бойынша циркуляциясына тең
-тің шекарасы бойынша циркуляциясына тең
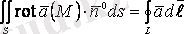
немесе
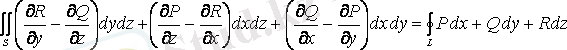 . (1. 9)
. (1. 9)
Ротордың қасиеттері
1.
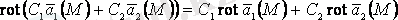 ;
;
2. егер
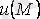 - скалярлық функция, ал
- скалярлық функция, ал
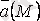 - вектор болса, онда
- вектор болса, онда
 .
.
Гамильтон операторы
Символдық
 - набла-векторын енгізейік.
- набла-векторын енгізейік.
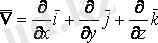 Гамильтон операторы деп аталады.
Гамильтон операторы деп аталады.
1.
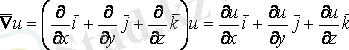 ,
,
 .
.
2.
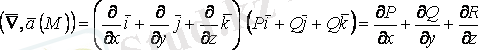 ,
,
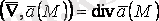 .
.
3.
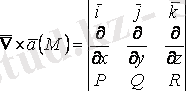 ,
,
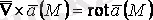 .
.
Өрістердің типтері
1. Егер
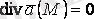 болса, онда
болса, онда
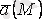 векторлық өрісі соленоидалдық немесе түтікшелік өріс болады.
векторлық өрісі соленоидалдық немесе түтікшелік өріс болады.
2. Егер
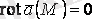 болса, онда
болса, онда
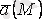 векторлық өрісі потенциалдық немесе құйынсыз өріс болады.
векторлық өрісі потенциалдық немесе құйынсыз өріс болады.
3. Егер векторлық өріс соленоидалдық та, потенциалдық та болса, онда ол гармониялық болады.
№ 2 дәріс Дифференциалдық теңдеулер. Жай дифференциалдық теңдеулер
Мазмұны: Негізгі анықтамалар және ұғымдар. Бірінші ретті дифференциалдық теңдеулердің түрлері, оларды шешу әдістері.
Дәрістің мақсаты: Дифференциалдық теңдеудің түрі мен ретін анықтауды, сәйкес ауыстыруларды қолдануды, дифференциалдық теңдеудің жалпы шешімін немесе жалпы интегралын табуды үйрету.
Негізгі анықтамалар және ұғымдар
2. 1
анықтама
Дифференциалдық теңдеу деп тәуелсіз айнымалы
 -ті, белгісіз функция
-ті, белгісіз функция
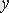 -ті және оның әртүрлі ретті туындыларын немесе дифференциалдарын байланыстыратын теңдеуді атайды.
-ті және оның әртүрлі ретті туындыларын немесе дифференциалдарын байланыстыратын теңдеуді атайды.
2. 2 анықтама Дифференциалдық теңдеуге кіретін туындының ең жоғары реті дифференциалдық теңдеудің реті деп аталады.
Мысал 2. 1 -
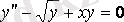 . Берілген теңдеу дифференциалдық теңдеу болады, өйткені оның құрамында белгісіз функцияның бірінші және екінші ретті туындылары бар. Бұл екінші ретті дифференциалдық теңдеу, себебі теңдеуге енгізілген туындылардың ең жоғары реті 2-ге тең.
. Берілген теңдеу дифференциалдық теңдеу болады, өйткені оның құрамында белгісіз функцияның бірінші және екінші ретті туындылары бар. Бұл екінші ретті дифференциалдық теңдеу, себебі теңдеуге енгізілген туындылардың ең жоғары реті 2-ге тең.
Мысал 2. 2 -
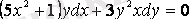 . Бұл теңдеу дифференциалдық теңдеу болады, өйткені оның құрамында белгісіз функцияның бірінші ретті дифференциалдары бар. Берілген теңдеу бірінші ретті дифференциалдық теңдеу.
. Бұл теңдеу дифференциалдық теңдеу болады, өйткені оның құрамында белгісіз функцияның бірінші ретті дифференциалдары бар. Берілген теңдеу бірінші ретті дифференциалдық теңдеу.
2. 3
анықтама
Дифференциалдық теңдеуді тепе-теңдікке айналдыратын кез-келген
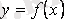 функциясы дифференциалдық теңдеудің шешімі немесе интегралы деп аталады.
функциясы дифференциалдық теңдеудің шешімі немесе интегралы деп аталады.
Бірінші ретті дифференциалдық теңдеулер
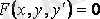 (2. 1)
(2. 1)
түріндегі теңдеу - бірінші ретті дифференциалдық теңдеудің жалпы түрі.
Егер (2. 1) теңдеуін бірінші ретті туындыға қарағанда шешуге болса, онда
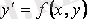 , (2. 2)
, (2. 2)
түріндегі теңдеу бірінші ретті дифференциалдық теңдеудің нормалды формасы немесе бірінші ретті туындысына қарағанда шешілген дифференциалдық теңдеу деп аталады.
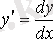 теңдігі орындалатынын ескеріп, (2. 2) -ні келесі түрге келтіруге болады
теңдігі орындалатынын ескеріп, (2. 2) -ні келесі түрге келтіруге болады
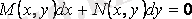 . (2. 3)
. (2. 3)
2. 4
анықтама
Бірінші ретті дифференциалдық теңдеуді тепе-теңдікке айналдыратын,
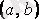 анықталған
анықталған
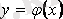 функциясы оның шешімі деп аталады.
функциясы оның шешімі деп аталады.
Дифференциалдық теңдеудің шешімінің графигі интегралдық қисық деп аталады.
Мынадай сұрақ туындайды: қандай шарттар орындалғанда (2. 2) теңдеуінің шешімі табылады? Бұл сұраққа (2. 2) дифференциалдық теңдеудің шешімінің бар болуы және жалғыздығы туралы Коши теоремасы деп аталатын теорема жауап береді.
Коши теоремасы.
Егер
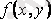 және оның
және оның
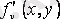 дербес туындысы
дербес туындысы
 жазықтығының кейбір
жазықтығының кейбір
 облысында анықталған және үзіліссіз болса, онда
облысында анықталған және үзіліссіз болса, онда
 облысының қандай да бір ішкі
облысының қандай да бір ішкі
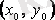 нүктесінің маңайында
нүктесінің маңайында
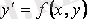 теңдеуінің
теңдеуінің
“
 болғанда
болғанда
 болады” (2. 4)
болады” (2. 4)
деген шарттарға қанағаттандыратын жалғыз шешімі бар болады.
(2. 4) шарттары - бастапқы шарттар деп аталады да
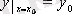 (2. 4’)
(2. 4’)
белгіленеді.
Егер де (2. 2) теңдеуінің (2. 4) бастапқы шарттарына қанағаттандыратын шешімін табу керек болса, Коши есебін шешу керек дейміз.
Геометриялық тұрғыдан Коши есебінің шешімін табу дегеніміз интегралдық қисықтар жиынынан
 жазықтығының берілген
жазықтығының берілген
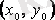 нүктесі арқылы өтетін қисықты алуды білдіреді.
нүктесі арқылы өтетін қисықты алуды білдіреді.
Жазықтықтың кейбір нүктелерінен бірнеше интегралдық қисық өтетін немесе ешбір интегралдық қисық өтпейтін нүктелері теңдеудің ерекше нүктелері деп аталады.
2. 5
анықтама
 -тен және еркін тұрақты
-тен және еркін тұрақты
 -дан тәуелді
-дан тәуелді
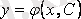 (2. 5)
(2. 5)
функциясы
а) тұрақты
 -ның кез келген мәнінде (2. 2) теңдеуіне қанағаттандырса,
-ның кез келген мәнінде (2. 2) теңдеуіне қанағаттандырса,
б) (2. 4) шарттары қандай болса да
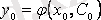 теңдігі орындалатындай еркін тұрақтының
теңдігі орындалатындай еркін тұрақтының
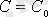 мәні табылса
мәні табылса
(2. 2) дифференциалдық теңдеуінің
 жазықтығының кейбір
жазықтығының кейбір
 облысындағы жалпы шешімі деп аталады.
облысындағы жалпы шешімі деп аталады.
2. 6 анықтама Дифференциалдық теңдеудің
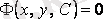 , (2. 6)
, (2. 6)
түрінде табылған шешімі (2. 2) -нің жалпы интегралы деп аталады.
2. 7 анықтама
(2. 2) теңдеуінің
 облысындағы дербес шешімі деп теңдеудің жалпы шешімі (2. 5) -тен еркін тұрақты
облысындағы дербес шешімі деп теңдеудің жалпы шешімі (2. 5) -тен еркін тұрақты
 -ның бекітілген
-ның бекітілген
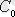 мәнінде алынған
мәнінде алынған
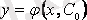 функциясын айтамыз.
функциясын айтамыз.
Бірінші ретті дифференциалдық теңдеудің геометриялық мағынасы
Айталық,
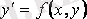 дифференциалдық теңдеуі берілсін және
дифференциалдық теңдеуі берілсін және
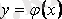 - оның шешімі болсын. Интегралдық қисықтың кез келген нүктесі арқылы жанама жүргізуге болады. Интегралдық қисыққа әрбір
- оның шешімі болсын. Интегралдық қисықтың кез келген нүктесі арқылы жанама жүргізуге болады. Интегралдық қисыққа әрбір
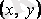 нүктесінде жүргізілген жанаманың бұрыштық коэффициенті
нүктесінде жүргізілген жанаманың бұрыштық коэффициенті
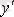 осы нүктедегі
осы нүктедегі
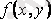 функциясының мәніне тең екені теңдеуден жеңіл байқалады. Демек,
функциясының мәніне тең екені теңдеуден жеңіл байқалады. Демек,
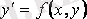 теңдігі нүктенің координаттары мен осы нүктеде интегралдық қисықтың графигіне жүргізілген жанаманың бұрыштық коэффициенті
теңдігі нүктенің координаттары мен осы нүктеде интегралдық қисықтың графигіне жүргізілген жанаманың бұрыштық коэффициенті
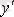 арасындағы тәуелділікті орнатады. Интегралдық қисықтың әрбір
арасындағы тәуелділікті орнатады. Интегралдық қисықтың әрбір
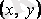 нүктесіне бұрыштық коэффициенті
нүктесіне бұрыштық коэффициенті
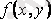 болатын бағытталған кесіндіні сәйкестендірейік, сонда берілген теңдеудің бағыттар өрісін аламыз.
болатын бағытталған кесіндіні сәйкестендірейік, сонда берілген теңдеудің бағыттар өрісін аламыз.
Сонымен, геометриялық тұрғыдан
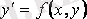 теңдеуі
теңдеуі
 жазықтығындағы бағыттар өрісін анықтайды, ал шешім - интегралдық қисық, оның әрбір нүктесінде жүргізілген жанаманың бағыты өрістің бағытымен беттеседі.
жазықтығындағы бағыттар өрісін анықтайды, ал шешім - интегралдық қисық, оның әрбір нүктесінде жүргізілген жанаманың бағыты өрістің бағытымен беттеседі.
Теңдеулердің түрлері
I.
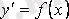 (2. 7)
(2. 7)
қарапайым дифференциалдық теңдеу деп аталады. Оны
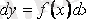 түрінде де жазуға болады.
түрінде де жазуға болады.
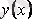 белгісіз функциясы
белгісіз функциясы
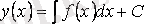 формуласымен анықталады.
формуласымен анықталады.
II.
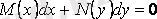 (2. 8)
(2. 8)
айнымалылары ажыратылған теңдеу деп аталады.
(2. 8) -дің шешімі
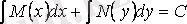 формуласымен анықталады.
формуласымен анықталады.
III.
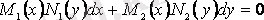 (2. 9)
(2. 9)
айнымалылары ажыратылатын теңдеу деп аталады.
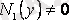 және
және
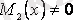 деп есептеп, (2. 9) теңдігінің екі жағын
деп есептеп, (2. 9) теңдігінің екі жағын
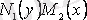 көбейтіндісіне бөлеміз, онда
көбейтіндісіне бөлеміз, онда
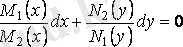 теңдеуін аламыз, яғни (2. 9) -ды айнымалылары ажыратылған дифференциалдық теңдеуге келтіріп аламыз.
теңдеуін аламыз, яғни (2. 9) -ды айнымалылары ажыратылған дифференциалдық теңдеуге келтіріп аламыз.
(2. 10)
айнымалылары ажыратылатын теңдеу, мұндағы
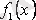 және
және
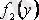 - үзіліссіз функциялар. (2. 10) -ның шешімін табу үшін
- үзіліссіз функциялар. (2. 10) -ның шешімін табу үшін
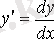 теңдігін ескеріп, берілген теңдеуді
теңдігін ескеріп, берілген теңдеуді
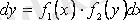 (2. 11)
(2. 11)
түрінде жазып аламыз.
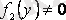 деп ұйғарып, (2. 11) -ді
деп ұйғарып, (2. 11) -ді
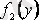 -ке бөлеміз, онда айнымалылары ажыратылған теңдеуді аламыз:
-ке бөлеміз, онда айнымалылары ажыратылған теңдеуді аламыз:
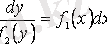 . Соңғы теңдіктің екі жағын интегралдап, (2. 10) теңдеуінің жалпы интегралын аламыз
. Соңғы теңдіктің екі жағын интегралдап, (2. 10) теңдеуінің жалпы интегралын аламыз
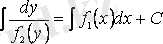 .
.
Мысал 2. 3 -
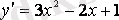 - бұл қарапайым бірінші ретті дифференциалдық теңдеу.
- бұл қарапайым бірінші ретті дифференциалдық теңдеу.
Интегралдаймыз
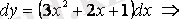
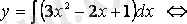
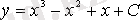 .
.
Мысал 2. 4 -
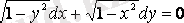 - бұл айнымалылары ажыратылатын дифференциалдық теңдеу.
- бұл айнымалылары ажыратылатын дифференциалдық теңдеу.
Теңдеудің екі жағын
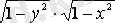 көбейтіндісіне бөлеміз, әрине алдын ала
көбейтіндісіне бөлеміз, әрине алдын ала
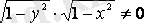 деп ұйғарамыз, онда айнымалылары ажыратылған теңдеуді аламыз
деп ұйғарамыз, онда айнымалылары ажыратылған теңдеуді аламыз
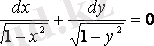 .
.
Осы теңдеуді интегралдап
 теңдігін табамыз.
теңдігін табамыз.
 формуласын пайдаланып, соңғы теңдікті
формуласын пайдаланып, соңғы теңдікті
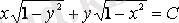
түрінде жазып аламыз. Бұл берілген дифференциалдық теңдеудің жалпы интегралы.
№ 3 дәріс Айнымалыларына қарағанда біртекті дифференциалдық
теңдеулер. Біртекті теңдеулерге келтірілетін теңдеулер.
І-ретті сызықтық дифференциалдық теңдеулер.
Бернулли теңдеуі
Мазмұны:
Функцияның біртектілік дәрежесін анықтау,
 ,
,
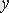 айнымалы-ларына қарағанда біртекті дифференциалдық теңдеулер. І-ретті сызықтық бір-текті және біртекті емес дифференциалдық теңдеулер. Еркін тұрақтыны вариациялау әдісі. Бернулли теңдеуі.
айнымалы-ларына қарағанда біртекті дифференциалдық теңдеулер. І-ретті сызықтық бір-текті және біртекті емес дифференциалдық теңдеулер. Еркін тұрақтыны вариациялау әдісі. Бернулли теңдеуі.
Дәрістің мақсаты:
Функцияның біртектілік дәрежесін анықтауды,
 ,
,
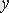 айнымалыларына қарағанда біртекті дифференциалдық теңдеулерді және оларға келтірілетін теңдеулерді шешуді, І-ретті біртекті және біртекті емес дифференциалдық теңдеулерді шешуді, еркін тұрақтыны вариациялау әдісін қолдануды, Бернулли теңдеуін шешуді үйрету.
айнымалыларына қарағанда біртекті дифференциалдық теңдеулерді және оларға келтірілетін теңдеулерді шешуді, І-ретті біртекті және біртекті емес дифференциалдық теңдеулерді шешуді, еркін тұрақтыны вариациялау әдісін қолдануды, Бернулли теңдеуін шешуді үйрету.
IV.
 және
және
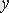 айнымалыларына қарағанда І-ретті біртекті дифференциал-дық теңдеулер.
айнымалыларына қарағанда І-ретті біртекті дифференциал-дық теңдеулер.
3. 1 анықтама
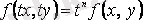 теңдігіне қанағаттандыратын
теңдігіне қанағаттандыратын
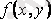 функциясы өлшемі
функциясы өлшемі
 -ші ретті біртекті функция деп аталады.
-ші ретті біртекті функция деп аталады.
Мысалы,
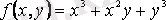 берілсін. Бұл функция үшін
берілсін. Бұл функция үшін
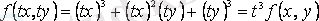 ,
,
яғни
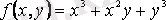 - өлшемі
- өлшемі
 -ші ретті біртекті функция.
-ші ретті біртекті функция.
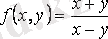 функциясы үшін
функциясы үшін
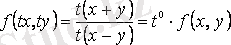 , яғни
, яғни
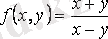 - өлшемі
- өлшемі
 -ші ретті біртекті функция.
-ші ретті біртекті функция.
3. 2 анықтама
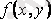 функциясы
функциясы
 ,
,
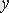 айнымалыларына қарағанда өлшемі
айнымалыларына қарағанда өлшемі
 -ші ретті біртекті функция болса
-ші ретті біртекті функция болса
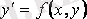 теңдеуі І-ретті біртекті дифференциалдық теңдеу деп аталады.
теңдеуі І-ретті біртекті дифференциалдық теңдеу деп аталады.
3. 3 анықтама
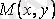 және
және
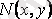 өлшем реттері бірдей функциялар болса
өлшем реттері бірдей функциялар болса
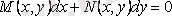 дифференциалдық теңдеуі
дифференциалдық теңдеуі
 ,
,
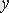 айнымалыларына қарағанда біртекті теңдеу болады.
айнымалыларына қарағанда біртекті теңдеу болады.
 және
және
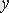 айнымалыларына қарағанда біртекті І-ретті дифференциалдық теңдеуді шешу үшін
айнымалыларына қарағанда біртекті І-ретті дифференциалдық теңдеуді шешу үшін
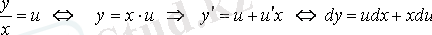 (3. 1)
(3. 1)
алмастыруын қолданып, III-ші түрдегі теңдеуге келтіру арқылы шешеді.
V.
 және
және
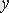 айнымалыларына қарағанда І-ретті біртекті дифференциал-дық теңдеуге келтірілетін теңдеулерге
айнымалыларына қарағанда І-ретті біртекті дифференциал-дық теңдеуге келтірілетін теңдеулерге
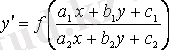 (3. 2)
(3. 2)
түріндегі теңдеулер жатады.
Шешуі: 1) егер
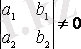 болса, онда
болса, онда
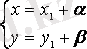 алмастыруын жасай-мыз, мұндағы
алмастыруын жасай-мыз, мұндағы
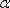 мен
мен
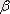 сызықтық теңдеулер жүйесінен
сызықтық теңдеулер жүйесінен
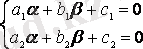 та-былады.
та-былады.
2) егер
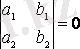 болса, онда
болса, онда
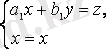 алмастыруын жасаймыз да, IV-ші түрдегі теңдеуге келтіреміз.
алмастыруын жасаймыз да, IV-ші түрдегі теңдеуге келтіреміз.
Сызықтық дифференциалдық теңдеулер
3. 4 анықтама VII
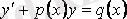 (3. 3)
(3. 3)
І-ретті сызықтық дифференциалдық теңдеу деп аталады, мұндағы
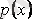 және
және
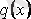 -
үзіліссіз функциялар. (3. 3) теңдеуіне белгісіз функция
-
үзіліссіз функциялар. (3. 3) теңдеуіне белгісіз функция
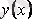 және оның туындысы
және оның туындысы
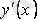 тек бірінші дәрежеде кіреді.
тек бірінші дәрежеде кіреді.
3. 5 анықтама
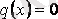 болса, (3. 3) І-ретті сызықтық біртекті дифференциалдық теңдеу болады да, VI-шы түрде жазылады
болса, (3. 3) І-ретті сызықтық біртекті дифференциалдық теңдеу болады да, VI-шы түрде жазылады
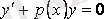 .
(3. 4)
.
(3. 4)
Егер
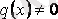 болса, онда (3. 3) І-ретті сызықтық біртекті емес дифферен-циалдық теңдеу болады.
болса, онда (3. 3) І-ретті сызықтық біртекті емес дифферен-циалдық теңдеу болады.
(3. 4) теңдеуінің шешімін табамыз. Ол үшін алдымен (3. 4) -ті айнымалы-лары ажыратылатын теңдеуге келтіреміз
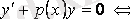

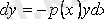 .
.
Енді айнымалыларын ажыратып алып, алынған теңдеуді интегралдаймыз
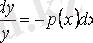 ,
,
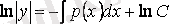 .
.
Сонымен,
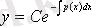 .
(3. 5)
.
(3. 5)
(3. 5) функциясы - (3. 4) -тің жалпы шешімі.
(3. 3) І-ретті сызықтық біртекті емес дифференциалдық теңдеудің шеші-мін табу алгоритмін келтірейік. (3. 3) -ті шешу үшін еркін тұрақтыны вариация-лау әдісін пайдаланамыз. Оның мағынасы мынада:
а) алдымен сәйкес (3. 4) түріндегі теңдеудің жалпы шешімін, яғни (3. 5) түріндегі функцияны табамыз;
б) (3. 5) -гі
 -ны
-ны
 -тен тәуелді белгісіз
-тен тәуелді белгісіз
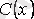 функциясы деп есептейміз. Енді (3. 3) -тің жалпы шешімін
функциясы деп есептейміз. Енді (3. 3) -тің жалпы шешімін
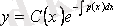 (3. 6)
(3. 6)
түрінде іздейміз.
Біздің ұйғаруымыз бойынша (3. 6) (3. 3) -тің шешімі болған соң, (3. 6) -ны (3. 3) -ке қойсақ, тепе-теңдік аламыз
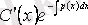
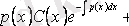
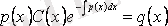
осыдан
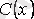 функциясын табамыз
функциясын табамыз
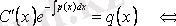
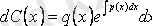
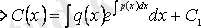 .
.
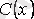 үшін табылған өрнекті (3. 6) -ға қоямыз да, (3. 3) дифференциалдық тең-деуінің жалпы шешімін табамыз:
үшін табылған өрнекті (3. 6) -ға қоямыз да, (3. 3) дифференциалдық тең-деуінің жалпы шешімін табамыз:
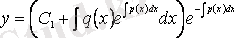 , оны
, оны
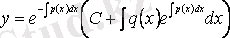 (3. 7)
(3. 7)
түрінде жазамыз.
(3. 7) - (3. 3) -тің жалпы шешімі, яғни (3. 7) - І-ретті сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімі.
І-ретті сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімінің құрамы
І-ретті сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімі сәйкес сызықтық біртекті дифференциалдық теңдеудің жалпы шешімі мен біртекті емес дифференциалдық теңдеудің кейбір дербес шешімінен құра-лады, яғни
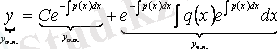 ,
,
 , мұндағы
, мұндағы
 - біртекті емес дифференциалдық теңдеудің жалпы шешімі,
- біртекті емес дифференциалдық теңдеудің жалпы шешімі,
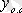 - біртекті диф-ференциалдық теңдеудің жалпы шешімі,
- біртекті диф-ференциалдық теңдеудің жалпы шешімі,
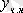 - біртекті емес дифференциал-дық теңдеудің дербес шешімі.
- біртекті емес дифференциал-дық теңдеудің дербес шешімі.
Мысал 3. 1 -
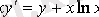 теңдеуінің жалпы шешімін табу керек.
теңдеуінің жалпы шешімін табу керек.
Шешуі:
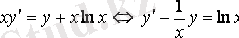 - бұл (3. 3) түріндегі дифференци-алдық теңдеу. Сәйкес біртекті теңдеуді жазып аламыз:
- бұл (3. 3) түріндегі дифференци-алдық теңдеу. Сәйкес біртекті теңдеуді жазып аламыз:
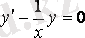 . Осыдан
. Осыдан
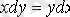 ,
,
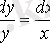 ,
,
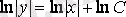 , - бұл сызықтық біртекті теңдеудің жалпы шешімі, яғни
, - бұл сызықтық біртекті теңдеудің жалпы шешімі, яғни
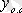 . Онда сызықтық біртекті емес теңдеудің жалпы шешімін
. Онда сызықтық біртекті емес теңдеудің жалпы шешімін
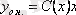 түрінде іздейміз.
түрінде іздейміз.
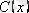 функциясын анықтаймыз:
функциясын анықтаймыз:
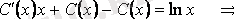
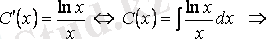
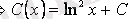 . Демек,
. Демек,
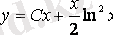 берілген теңдеудің жалпы шешімі болады.
берілген теңдеудің жалпы шешімі болады.
Бернулли теңдеуі
VIII
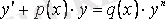 (3. 8)
(3. 8)
түріндегі теңдеу Бернулли теңдеуі деп аталады.
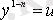 алмастыруын орындағаннан кейін (
алмастыруын орындағаннан кейін (
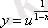 ,
,
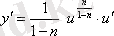 ) Бернулли теңдеуі VII-ші түрдегі теңдеуге келтіріледі.
) Бернулли теңдеуі VII-ші түрдегі теңдеуге келтіріледі.
Ескерту.
VII.
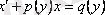 - белгісіз
- белгісіз
 функциясы үшін І-ретті сызықтық біртекті емес дифференциалдық теңдеу.
функциясы үшін І-ретті сызықтық біртекті емес дифференциалдық теңдеу.
VI.
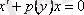 - белгісіз
- белгісіз
 функциясы үшін І-ретті сызықтық біртекті дифферен-циалдық теңдеу.
функциясы үшін І-ретті сызықтық біртекті дифферен-циалдық теңдеу.
VIII.
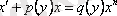 - белгісіз
- белгісіз
 функциясы үшін Бернулли теңдеуі.
функциясы үшін Бернулли теңдеуі.
Толық дифференциалдардағы теңдеу
3. 5 анықтама
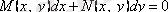 (3. 9)
(3. 9)
түріндегі теңдеу
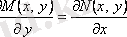 (3. 10)
(3. 10)
шарты орындалғанда толық дифференциалдардағы теңдеу деп аталады.
(3. 10) шарты орындалғанда (3. 9) -дың сол жағы кейбір
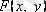 функция-сының дифференциалы болатынын, яғни
функция-сының дифференциалы болатынын, яғни
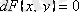 , дәлелдейміз.
, дәлелдейміз.
Қажеттілік.
(3. 9) -дың сол жағы
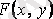 үшін толық дифференциал болсын:
үшін толық дифференциал болсын:
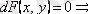
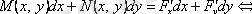
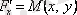 және
және
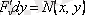 , онда
, онда
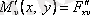 және
және
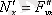 .
.
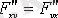 болғандықтан,
болғандықтан,
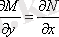 болады.
болады.
Жеткіліктілік.
(3. 10) орындалсын, яғни
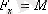 ,
,
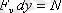 , онда
, онда
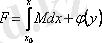 және
және
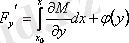
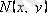 . Басқа жағынан,
. Басқа жағынан,
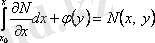 , осыдан
, осыдан
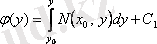 , онда
, онда
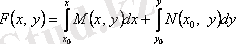 . Сонымен, (3. 9) -дың сол жағы
. Сонымен, (3. 9) -дың сол жағы
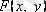 функциясының толық дифференциалы болады, ал (3. 9) теңдеуінің жалпы шешімі
функциясының толық дифференциалы болады, ал (3. 9) теңдеуінің жалпы шешімі
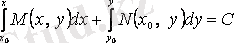 формуласымен анықталады.
формуласымен анықталады.
№ 4 дәріс Жоғары ретті дифференциалдық теңдеулер.
Реті төмендетілетін дифференциалдық теңдеулер.
Жоғары ретті сызықтық дифференциалдық теңдеулер
Мазмұны: Негізгі ұғымдар мен анықтамалар. Екінші ретті сызықтық дифференциалдық теңдеулер. Біртекті сызықтық дифференциалдық теңдеудің шешімінің негізгі қасиеті. Сызықты тәуелді және сызықты тәуелсіз функциялар жүйесі, олардың вронскианы.
Дәрістің мақсаты: Жоғары ретті дифференциалдық теңдеудің анықтамасы. Реті төмендетілетін дифференциалдық теңдеулерді шешу тәсілдерін көрсету. Сызықтық біртекті және біртекті емес жоғары ретті дифференциалдық теңдеулер. Функциялар жүйесінің сызықтық тәуелділігі немесе тәуелсіздігін анықтауды үйрету.
4. 1 анықтама
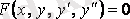 теңдеуі екінші ретті дифференциалдық теңдеуі деп аталады, мұндағы
теңдеуі екінші ретті дифференциалдық теңдеуі деп аталады, мұндағы
 - тәуелсіз айнымалы,
- тәуелсіз айнымалы,
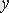 - белгісіз функция,
- белгісіз функция,
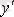 және
және
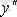 - оның туындылары.
- оның туындылары.
Көп жағдайда
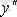 -ке қарағанда шешілген теңдеу қарастырылады
-ке қарағанда шешілген теңдеу қарастырылады
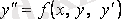 . (4. 1)
. (4. 1)
(4. 1) теңдеуінің шешімі деп
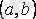 -да анықталған, теңдеуге қойғанда оны тепе-теңдікке айналдыратын
-да анықталған, теңдеуге қойғанда оны тепе-теңдікке айналдыратын
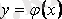 функциясы аталады. Шешімнің графигі интегралдық қисық деп аталады.
функциясы аталады. Шешімнің графигі интегралдық қисық деп аталады.
Коши теоремасы.
Егер
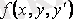 және оның
және оның
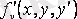 ,
,
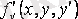 дербес туындылары
дербес туындылары
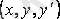 айнымалылар кеңістігінің кейбір
айнымалылар кеңістігінің кейбір
 облысында анықталған және үзіліссіз болса, онда
облысында анықталған және үзіліссіз болса, онда
 облысының қандай да бір ішкі
облысының қандай да бір ішкі
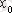 нүктесінің маңайында
нүктесінің маңайында
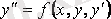 теңдеуінің
теңдеуінің
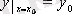 ,
,
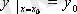 . (4. 2)
. (4. 2)
шарттарға қанағаттандыратын жалғыз шешімі бар болады. (4. 2) - бастапқы шарттар.
Дифференциалдық теңдеудің бастапқы шарттарға қанағаттандыратын шешімін табу есебін Коши есебі дейміз.
Геометриялық тұрғыдан Коши есебінің шешімін табу дегеніміз интегралдық қисықтар жиынынан
 жазықтығының берілген
жазықтығының берілген
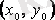 нүктесі арқылы өтетін, осы нүктедегі жанамасының бұрыштық коэффициенті
нүктесі арқылы өтетін, осы нүктедегі жанамасының бұрыштық коэффициенті
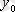 болатын қисықты алуды білдіреді.
болатын қисықты алуды білдіреді.
4. 2 анықтама
 -тен және екі еркін тұрақты
-тен және екі еркін тұрақты
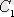 мен
мен
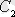 -ден тәуелді
-ден тәуелді
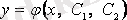 функциясы кейбір
функциясы кейбір
 облысында (4. 1) теңдеуінің жалпы шешімі болады, егер ол: 1)
облысында (4. 1) теңдеуінің жалпы шешімі болады, егер ол: 1)
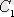 мен
мен
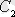 тұрақтыларының кез келген мәндерінде шешім болса; 2) кез келген (4. 2) бастапқы шарттары үшін
тұрақтыларының кез келген мәндерінде шешім болса; 2) кез келген (4. 2) бастапқы шарттары үшін
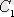 ,
,
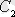 тұрақтыларының сәйкесінше
тұрақтыларының сәйкесінше
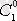 ,
,
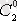 жалғыз ғана мәндері табылып,
жалғыз ғана мәндері табылып,
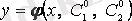 функциясы бастапқы шарттарға қанағаттандырса.
функциясы бастапқы шарттарға қанағаттандырса.
4. 3 анықтама
Жалпы шешім -
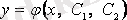 функциясынан
функциясынан
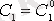 ,
,
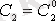 мәндерінде шығатын кез келген
мәндерінде шығатын кез келген
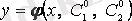 функциясы (4. 1) теңдеуінің дербес шешімі деп аталады.
функциясы (4. 1) теңдеуінің дербес шешімі деп аталады.
Жоғары ретті дифференциалдық теңдеулер
n -ретті дифференциалдық теңдеу деп
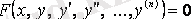
түріндегі теңдеу аталады. Егер де ол жоғары ретті туындысына қарағанда шешілген болса, онда n -ретті дифференциалдық теңдеу
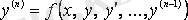 (4. 3)
(4. 3)
түрінде жазылады.
(4. 3) -тің шешімі деп
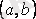 -да анықталған, (4. 3) -ке қойғанда оны тепе-теңдікке айналдыратын
-да анықталған, (4. 3) -ке қойғанда оны тепе-теңдікке айналдыратын
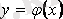 функциясы аталады.
функциясы аталады.
(4. 3) -тің жалпы шешімі
х-
тен және
n
еркін тұрақтыдан тәуелді болады:
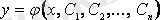 .
.
Жалпы шешімнен
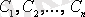 тұрақтыларының бекітілген мәндерінде пайда болатын (4. 3) -тің шешімі оның дербес шешімі деп аталады.
тұрақтыларының бекітілген мәндерінде пайда болатын (4. 3) -тің шешімі оның дербес шешімі деп аталады.
Жоғары ретті теңдеу үшін бастапқы шарттар
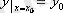 ,
,
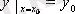 , …,
, …,
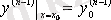 (4. 4)
(4. 4)
түрінде жазылады.
(4. 3) теңдеуінің (4. 4) бастапқы шарттарына қанағаттандыратын шешімін табу есебін Коши есебін шешу дейміз.
Реті төмендетілетін дифференциалдық теңдеулер
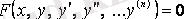 немесе
немесе
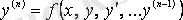 (4. 5)
(4. 5)
дербес жағдайларын қарастырамыз.
1.
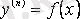 теңдеуі. Бұл теңдеуде
теңдеуі. Бұл теңдеуде
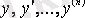 жоқ, оның шешімін бірте-бірте интегралдау көмегімен табамыз:
жоқ, оның шешімін бірте-бірте интегралдау көмегімен табамыз:
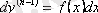 ,
,
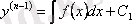 ,
,
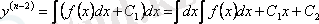 , …,
, …,
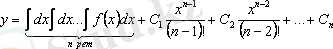 .
.
2.
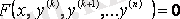 теңдеуі. Бұл теңдеуге
теңдеуі. Бұл теңдеуге
 және оның
және оның
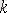 -шы ретке дейінгі туындылары кірмеген. Алмастыру жасаймыз:
-шы ретке дейінгі туындылары кірмеген. Алмастыру жасаймыз:
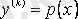 ,
,
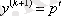 , …,
, …,
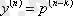 ,
,
 теңдеуін аламыз. Берілген теңдеудің ретті
теңдеуін аламыз. Берілген теңдеудің ретті
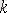 -ға төмендеді.
-ға төмендеді.
3.
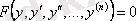 теңдеуі. Бұл теңдеуде
теңдеуі. Бұл теңдеуде
 айнымалысы айқын түрде жоқ. Алмастыру орындаймыз:
айнымалысы айқын түрде жоқ. Алмастыру орындаймыз:
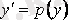 . Енді
. Енді
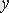 -ті тәуелсіз айнымалы деп есептейміз, онда
-ті тәуелсіз айнымалы деп есептейміз, онда
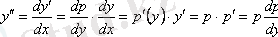 ,
,
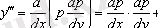
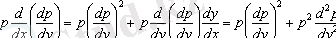 ,
,
т. с. с. Нәтижесінде
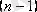 -ші ретті теңдеуді аламыз.
-ші ретті теңдеуді аламыз.
Жоғары ретті сызықтық дифференциалдық теңдеулер
 -ші ретті сызықтық дифференциалдық теңдеу деп
-ші ретті сызықтық дифференциалдық теңдеу деп
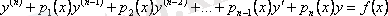
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz