САЛУ ЕСЕПТЕРІН ШЕШУДІҢ ӘДІСТЕРІ

Жұмыс түрі: Диссертация
Тегін: Антиплагиат
Көлемі: 61 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ
3
1
ГЕОМЕТРИЯЛЫҚ САЛУЛАР ТЕОРИЯСЫНЫҢ НЕГІЗДЕРІ
5
1.1
Конструктивті геометрияның жалпы аксиомалары
5
1.2
Салу есебі
7
1.3
Салу есебін шешу схемасы
14
2
САЛУ ЕСЕПТЕРІН ШЕШУДІҢ ӘДІСТЕРІ
22
2.1
Параллель көшіру әдісі
22
2.2
Ұқсастық әдісі
24
2.3
Гомотетия әдісі
30
2.4
Нүктелердің геометриялық орындары әдіс
32
2.5
Алгебралық әдіс
34
2.6
Симметрия әдісі
36
3
САЛУ ЕСЕПТЕРІН ШЕШУДІҢ ЕРЕКШЕЛІКТЕРІ
42
3.1
Салу есептерін шешу әдістемесінің ерекшеліктері
42
3.2
Салу есептерін шешуге үйретуге арналған әдістемелік ұсыныстар
45
3.3
Геометриялық орындар әдісінің ерекшеліктері
49
3.4
Алгебралық әдіс арқылы салу есептерін шешу ерекшеліктері
51
3.5
Осьтік симметрия әдісімен салу есептерін ешудің ерекшеліктері
53
3.6
Центрлік симметрия әдісімен салу есептерін ешудің ерекшеліктері
56
3.7
Параллель көшіру әдісімен салу есептерін ешудің ерекшеліктері
57
3.8
Ұқсастық әдісімен салу есептерін шешудің ерекшеліктері
59
3.9
Мектеп курсында салу есептерін шешуде GeoGebra бағдарламасын пайдаланудың артықшылығы
61
ҚОРЫТЫНДЫ
64
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
65

КІРІСПЕ

Зерттеу тақырыбының өзектілігі. Геометриялық салулар оқушының математикалық дайындығында маңызды рөл атқарады. Есептердің бірде-бір түрі оқушының математикалық шығармашылығы мен логикалық дағдыларын дамыту үшін геометриялық есептер сияқты маңызға ие емес. Бұл есептер оқушыларға стандартты көзқарас пен формальды қабылдауға жол бермейді. Салу есептері мектептегі геометрия курсының кез-келген бөлімінде оқушылардың теориялық білімдерін бекітуге ыңғайлы. Геометриялық салу есептерін шеше отырып, оқушы көптеген пайдалы ұқыптылық, бірізділік, логикалық, сурет салу сияқты дағдыларды дамыта алады.
Магистрлік диссертацияның мақсаты: мектеп курсы геометриясының планимериялық салу есептерін шешу әдістерін зерттеу.
Осы мақсатқа жету үшін мынадай міндеттер қойылды:
- әртүрлі салу есептері тақыбында әдебиеттермен жұмыс жасау;
- салу есептерін шешудің әдістерін меңгеру;
- салу есептерінің ерекшеліктерін айқындау;
- мектеп курсындағы әртүрлі планиметриялық салу есептерін шешу.
Магистрлік диссертацияның ғылыми жаңалығы.
- салу есептерін шешудің әдістері жүйелендірілді;
- салу есептері зерттелді;
- планимерияның әртүрлі салу есептері әртүрлі тәсілдермен шешілді.
Қорғayғa ұcынылғaн негiзгi ғылыми тұжырымдaр.
Зерттеу барысында ережелер, тұжырымдар мен ұсыныстар тұжырымдалды, олардың ішіндегі ең маңыздыларын мыналар деп санауға болады:
мектеп курсында логикалық және шығармашылық дағдыны дамытатын ең маңызды есептердің бірі - салу есептері;
салу есептерін әртүрлі тәсілдермен шешуге болады;
салу есептері күрделілігі жоғары есептер сантынан;
математикалық білімдерді қалыптастыру және дамыту үшін салу есептерінің маңызы зор.
Зерттеу жұмысының ғылыми және тәжірибелік мәні.
Геометриялық салу есептерін шешу кез келген оқушының қолынан келе бермейді, кейбіреулері үшін тіпті қызықсық, қажетсіз боп көрінуі де мүмкін. Тек циркуль мен сызғышты пайдаланып салудың қандай қажеті бар? - деген сауалдың да туындауы ғажап емес. Заманауи технологиялардың көмегімен геометриялық салуды әп-әдемі, көрнекі, дәл етіп орындап алуға болса және де сызғыш пен циркульдің ғана көмегімен орындау мүмкін емес есептерді шешіп беріп отырса, онда оған соншалықты қиналудың маңызы қандай деген сауал да алынуы мүмкін. Салу есептерінсіз геометрияның геометрия болуы, ағаштың жапырақтарсыз қалуымен пара-пар. Ол әдебиттегі бояуы мен баламасы жоқ, сылдыр құрғақ сөзбен тең. Геометрияны түсіну үшін салу есептерінің маңызы орасан зор. Тек оған деген қызығушылықты оята білу керек.
Зерттеудің теориялық және әдіснамалық негіздері.
Зерттеуде баяндалған материалдар және алынған нәтижелер геометрияның теориялық негізіне сай келеді және әдістемелік тұрғыдан негізделген.
Зерттеу объектісі: планиметрияның салу есептері.
Зерттеу пәні: мектеп геометриясы.
Зерттеу нәтижесінің сыннан өтуі мен жариялануы.
Зерттеу жұмысының теориялық қорытындылары Ғылым мен білімді дамытудың өзекті мәселелері атты Уәлиев оқулары-2020 Халықаралық ғылыми тәжірибелік онлайн-конференция материалдарының жинағында Жаратылыстану есептерін шешуде дифференциалдық теңдеулерді қолдану және Шығыстың аймақтық жаршысы журналының №2 басылымында Салу есептері және оларды шешудің ерекшіліктері атты мақалалар арқылы жарияланып, конференцияда баяндалған.
Магистрлік диссертация тақырыбы бойынша жалпы көлемі 0,7 шартты баспа табақ 2 ғылыми мақала жарияланды.
Жұмыстың құрылымы мен көлемі. Магистрлік диссертацияның көлемі 65 бет. Ол кіріспеден, үш тараудан, қорытындыдан, қолданылған әдебиеттер тізімінен, 37 суреттен тұрады.

1 ГЕОМЕТРИЯЛЫҚ САЛУЛАР ТЕОРИЯСЫНЫҢ НЕГІЗДЕРІ

1.1 Конструктивті геометрияның жалпы аксиомалары

Кез-келген нүктелер жиынтығын, егер, құрамында кем дегенде бір нүктесі бар болса, геометрияда фигура деп атайды.
Кеңістікте белгілі бір жазықтық берілген деп есептейміз, оны негізгі жазықтық деп атаймыз. Біз тек осы жазықтыққа жататын фигураларды қарастырумен шектелеміз.
Бір пішінді екінші пішіннің бөлігі деп атайды, егер бірінші кескіннің әрбір нүктесі екінші пішінге жататын болса. Мәселен, мысалы, түзудің бөліктері: оған жататын кез-келген кесінді, осы түзуде жатқан сәуле, осы түзудегі нүкте, түзудің өзі болады.
Екі немесе одан да көп фигуралардың байланысы дегеніміз - осы пішіндердің кем дегенде біреуіне жататын барлық нүктелердің жиынтығы.
Екі немесе одан да көп фигуралардың қиылысы немесе ортақ бөлігі - бұл фигураларға ортақ барлық нүктелердің жиынтығы.
Екі Ф мен Ф фигураларының айырымы дегеніміз Ф фигурасына жатпайтын Ф фигураның барлық нүктелерінің жиынтығы.
Екі фигураның қиылысында немесе айырмасында ешқандай нүкте болмайтын жағдайлар болады екен. Бұл жағдайда фигуралардың қиылысы немесе сәйкесінше айырымы нүктелердің бос жиынтығы деп айтады.
Геометриялық салулар зерттелетін геометрия бөлімі конструктивті геометрия деп аталады. Конструктивті геометрияның негізгі ұғымы - геометриялық фигураны салу ұғымы [1].
Егер фигура берілген десе, онда ол бейнеленген, сызылған, яғни салынған деген сөз. Сонымен, конструктивтік геометрияның бірінші негізгі талабы келесідей:
1. Берілген фигура салынған.
Берілген фигура және фигура оның элементтері арқылы көрсетілген немесе анықталған ұғымын шатастырмау керек екендігін ескеру керек [1].

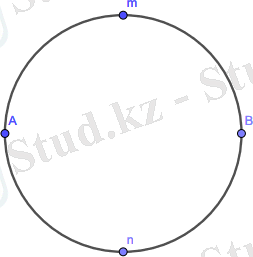
Сурет 1.1 - AmBnA шеңбері

Сурет 1.2 - МN түзуі

АmВ жартылай шеңбері салынғанын елестетіп көрейік, сонымен қатар АnВ жартылай шеңбері салынған. Әрине, осыдан кейін біз AmBnA шеңбері салынған деп ойлауымыз керек. 1.1 суретте көрсетілгендей, дәл сол сияқты, егер АМ сәулесі қандай да бір түзу сызықпен салынса, онда кейін BN сәулесі МN түзуі, сол түзу салынған деп саналса, 1.2 суретте көрсетілгендей, онда, әрине, бұл байланыс осы сәулелердің бұл мысалдары келесі постулаттың мағынасын айқындайды:
2. Егер екі (немесе одан да көп) фигура тұрғызылса, онда бұл фигуралардың байланысы да құрылады [1].

Сурет 1.3 - фигуралар байланысы

Бір түзудің екі кесіндісі салынған деп елестетіп көрейік: AB және CD. Әрине, CD кесіндісі толығымен АВ кесіндісіне жатады ма немесе жоқ па деген сұраққа жауап беруге болады деп саналады. Егер шеңбер мен нүкте салынған болса, онда суретті тікелей қарау арқылы салынған нүкте салынған шеңберде жатыр ма, жоқ па деген сұраққа жауап беруге болады. Жалпы, егер екі фигура тұрғызылса, онда олардың бірінің екіншісінің бөлігі екендігі немесе болмайтындығы белгілі болып саналады.
Геометриялық салулар теориясының үшінші негізгі талабын былайша өрнектеуге болады:
3. Егер екі фигура тұрғызылса, онда олардың айырымы бос жиын болғанын немесе болмайтынын анықтауға болады.
A, B, C, D түзудің төрт нүктесі болсын. AB және CD кесінділері салынды деп есептейік. Содан кейін, әрине, біз АВ кесіндісі ретінде қарастырамыз, ол AC және BD кесінділерінің айырмашылығы, ал CD кесінді, бұл BD және AC кесінділерінің арасындағы айырмашылық.
4. Егер екі салынған фигуралардың айырымы бос жиын болмаса, онда бұл айырым салынады.
Екі түзу сызып, олардың қиылысқан-қиылмағандығын әрқашан айтуға болады деп санаймыз. Дәл сол сияқты, егер екі шеңбер салынса, онда олардың ортақ нүктелері бар-жоғын орнатуға болады деп санаймыз. Бұл кез-келген екі фигураларға қатысты. Осылайша:
5. Егер екі фигура тұрғызылса, онда олардың қиылысы бос жиын болғанын немесе болмайтынын анықтауға болады.
Сурет салу тәжірибесі тұрғысынан соңғы шарт орындалған сызбалардың сапасына қойылатын белгілі бір талаптарды көрсетеді. Сонымен, мысалы, егер белгілі бір шеңбер мен нүкте тұрғызылса, онда нүктенің шеңберге жата-жатпайтындығы анық болуы керек. Егер екі шеңбер салынған болса, онда олардың ортақ нүктелері бар немесе жоқ деп айта аламыз.
AC және BD кесінділері салынғандығы белгілі болсын. Бұл жағдайда біз ВС кесіндісі салынған деп есептейміз, бұл осы екі кесіндінің. Егер қиылысатын екі шеңбер сызылса, онда олардың қиылысқан нүктелерінің жұбын да қарастырамыз. Мұндай келісімдер келесідей:
6. Егер екі салынған фигуралардың қиылысы бос болмаса, онда ол салынады.
Келесі үш негізгі талап - бір нүктені жоспарлау мүмкіндігі туралы.
7. Егер сізде осындай нүктелер болса, салынған екі фигураның ортақ нүктелерінің кез келген ақырғы санын салуға болады.
8. Салынған фигураға жататыны белгілі нүкте салуға болады.

1.2 Салу есебі

Салу есебі дегеніміз - бұл қандай деректермен, қандай құралдармен, қандай геометриялық фигураны салу керек екенін (жазықтықта сызу), бұл фигура белгілі бір шарттарды қанағаттандыратындығын білдіреді.
Циркуль мен сызғышты пайдалану арқылы салу есебін шешу оны алдын-ала мүмкін деп есептелетін бес қарапайым салулар жиынтығына келтіруді білдіреді [2]. Оларды тізіп көрейік.
1. Егер А және В екі нүкте тұрғызылса, онда оларды қосатын АВ түзу сызығы, сонымен қатар АВ кесіндісі және АВ және ВА сәулелерінің кез-келгені (сызғыш аксиомасы) салынады. 1.4 суретте көрсетілгендей.

Сурет 1.4 - фигуралар байланысы

2. Егер О нүктесі мен АВ кесіндісі тұрғызылса, онда центрі О нүктесінде және радиусы АВ болатын шеңбер, сондай-ақ осы шеңбердің кез келген доғасы салынады [2].
3. Егер екі түзу салынса, онда олардың қиылысу нүктесі салынады (егер ол бар болса). 1.5 суретте кескінделген.

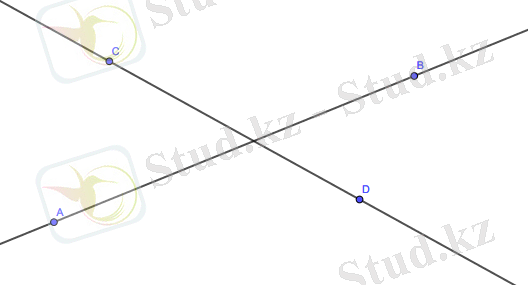
Сурет 1.5 - екі түзудің қиылысуы

4. Егер түзу мен шеңбер тұрғызылса, онда олардың қиылысу нүктелерінің кез-келгені салынады (егер ол бар болса). 1.6 суретте кескінделген.

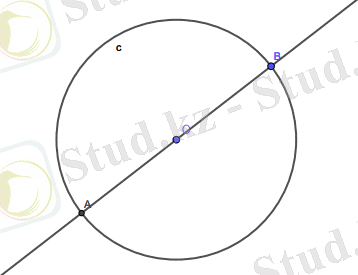
Сурет 1.6 - түзу мен шеңбер қиылысуы

5. Егер екі шеңбер тұрғызылса, онда олардың кез-келген қиылысу нүктелері салынады (егер ол бар болса). 1.7 суретте кескінделген.

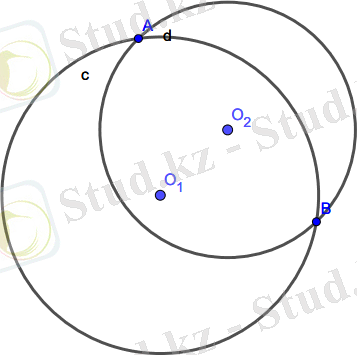
Сурет 1.7 - Екі шеңбердің қиылысуы

Қарпайым негізгі салуларға бір мысал қарастырып өтейік.
Берілген бұрышқа тең бұрыш салу. Берілген бұрыш ∠АВС болсын. Сәуле нүктеде және бұрышта болсын. В нүктесі центр болатын, кез келген радиусты шеңбер саламыз. Шеңбердің сәулелермен қиылысу нүктелерін А' және С' деп белгілейік.

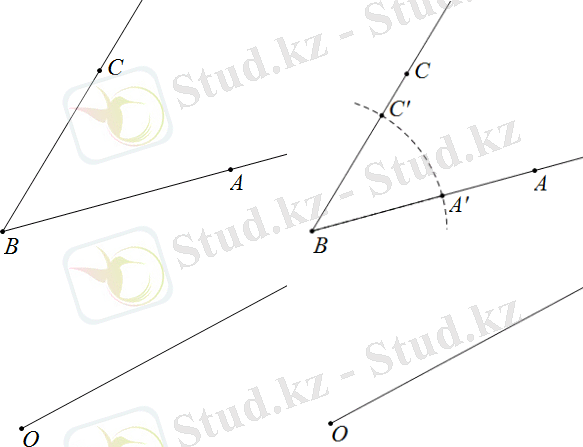
Сурет 1.8 - Берілген бұрышқа тең бұрыш салу

Радиус нүктесінде центрі бар шеңбер саламыз. Шеңбердің сәулемен қиылысу нүктесін белгілейміз. Радиус нүктесінде центрі бар шеңбер саламыз. Біз шеңберлердің қиылысу нүктесін белгілейміз [3]. Сәуле жүргізейік.

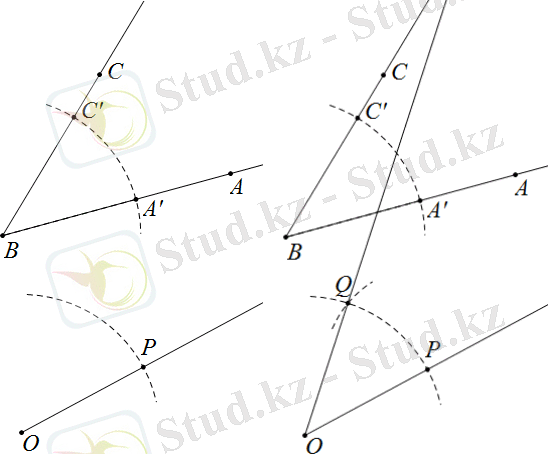
Сурет 1.8' - Берілген бұрышқа тең бұрыш салу, жалғасы

Берілген бұрышқа тең бұрыш аламыз, өйткені үшбұрыштар үш қабырғасы бойынша тең.
Кесіндіге орта перпендикуляр салу. Кесіндінің ұштарын центрлер етіп, еркін радиусты екі қиылысатын шеңберін саламыз. Олардың қиылысу нүктелерін қосып, орта перпендикуляр аламыз. Сурет 1.10 көрсетілген.

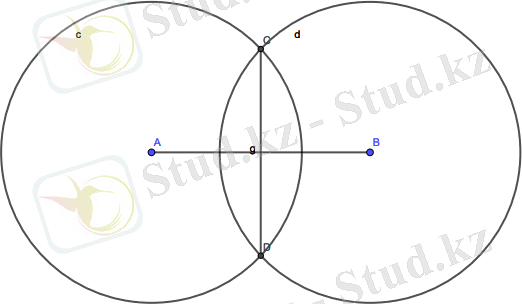
Сурет 1.9 - Кесіндіге орта перпендикуляр салу

Бұрыштың биссектрисасын салу. Бірінші бұрышты салып аламыз. Оның алгоритмін білеміз, оған тоқталмаймыз.

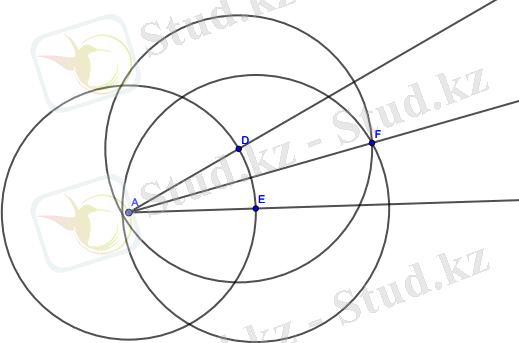
Сурет 1.10 - Бұрыштың биссектрисасын салу

Бұрыштың төбесін центр етіп алып шеңбер жүргіземіз. Ол бұрыштың қабырғаларымен қиылысады. Қиылысуында D, E нүктелері пайда боладыы. Осы нүктелерді центр етіп алып екі радиустары бірдей болатын шеңберлерді жүргіземіз. Екі шеңбердің қиылысу нүктесі мен бұрыштың төбесін қосамыз. Пайда болған сәуле бұрышты тең екіге бөледі, яғни биссектрисса пайда болады. Сөйтіп, біз бұрыштың бисекторын аламыз.
Екі кесіндінің қосындысын салу. Берілген сәуледе осы екі кесіндінің қосындысына тең кесінді салу үшін берілген кесінді салу әдісін екі рет қолдану керек. 1.10 суретте көрсетілген.

Сурет 1.11 - Екі кесіндінің қосындысы

Әрбір есептің шешімін қарапайым салуларға келтіру шешімді табуды қиындатады. Сондықтан есептің шешімі көбінесе негізгі салуларға дейін келтіріледі. Кейбір салуларды негізгілері ретінде қабылдау, таңдау белгілі бір дәрежеде ерікті. Мысалы, келесі салуларды негізгі салулар ретінде қарастыруға болады: берілген бұрышты жартыға бөлу; берілгенге тең кесінді құру; берілгенге тең бұрыш құру; параллель түзу салу, перпендикуляр түзу салу, берілген кесінді бөлу; үш қабырғасы, екі қабырғасы және олардың арасындағы бұрышы бойынша, бір қабырғасы және оған іргелес екі бұрышы бойынша үшбұрыш салу; гипотенуза мен катеттің бойымен тік бұрышты үшбұрыш салу [4-5].
Салу есебін шешу үшін оның барлық шешімдерін табу керек.
Соңғы анықтама біраз түсіндіруді қажет етеді.
Есептің шартын қанағаттандыратын фигуралар пішіні жағынан да, өлшемдерімен де, жазықтықтағы орналасуымен де ерекшеленуі мүмкін. Жазықтықтағы позициядағы айырмашылықтар салу есебінің өзі тұжырымдалуына байланысты ескеріледі немесе есепке алынбайды, атап айтқанда, есептің шарты қалаған фигураның белгілі бір орналасуын көздейтіндігіне байланысты.
Келесі қарапайым есепті қарастырайық: үш қабырғасы және олардың арасына бұрыш бойынша үшбұрыш салыңыз. Бұл есептің нақты мағынасы келесідей: үшбұрышты оның екі қабырғасы сәйкесінше берілген екі кесіндіге, ал олардың арасындағы бұрыш берілген бұрышқа тең болатындай етіп тұрғыз. Мұнда қажетті фигура (үшбұрыш) берілген фигуралармен (екі кесінді және бұрыш) тек теңдік қатынастарымен байланысады, ал қажетті үшбұрыштың осы фигураларға қатысты орналасуы немқұрайды. Сурет 1.12 көрсетілген.

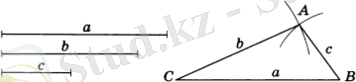
Сурет 1.12 - Үш қабырғасы бойынша үшбұрыш салу

Бұл жағдайда есептің шартын қанағаттандыратын АВС үшбұрышын салу оңай. АВС үшбұрышына тең барлық үшбұрыштар есептің шартын да қанағаттандырады. Алайда бұл үшбұрыштарды осы есептің әртүрлі шешімдері ретінде қарастырудың мағынасы жоқ, өйткені олар бір-бірінен жазықтықтағы орналасуымен ғана ерекшеленеді, бұл туралы есеп шығаруда ештеңе айтылмаған. Сондықтан, мәселенің ерекше шешімі бар деп есептейміз.
Сонымен, егер есептің шарты осы фигураларға қатысты қажетті фигураның белгілі бір орналасуын қарастырмаса, онда біз есептің шартын қанағаттандыратын барлық тең емес фигураларды іздеуге келісеміз. Мұндай мәселелер теңдікке дейін шешіледі деп айтуға болады. Бұл дегеніміз, егер: 1) есептің шарттарын қанағаттандыратын F1, F2, ... Fn тең емес фигуралардың белгілі бір саны салынған болса, және 2) шарттарын қанағаттандыратын кез-келген фигура екендігі дәлелденсе, есеп шешілді деп есептеледі. мәселе осы фигуралардың біріне тең. Бұл жағдайда есептің n әр түрлі шешімдері бар деп саналады.
Енді сәл өзгеше мазмұндағы мәселені қарастырайық: үшбұрыш салу үшін, берілген ВС кесіндісі оның бір жағы ретінде, екінші жағы берілген екінші кесіндісіне тең, ал олардың арасындағы бұрыш берілгенге тең болатындай етіп құру. α бұрышы. [4-5].
Бұл жағдайда есептің шарты осы фигуралардың біріне қатысты қажетті үшбұрыштың белгілі бір орналасуын қамтамасыз етеді (атап айтқанда, ВС кесіндісіне қатысты). Осыған орай, біз осы проблеманың барлық шешімдерін құру туралы сұраққа басқаша қараймыз. Көріп отырғанымыздай, осы есептің шартын қанағаттандыратын төрт үшбұрыш болуы мүмкін. Олар бір-біріне тең, бірақ осы BC фигурасына қатысты әртүрлі орналасқан. Бұл жағдайда есептің толық шешімі осы үшбұрыштардың барлығын салуды көздейді. Есептің берілген фигураға қатысты орналасуымен ерекшеленетін төрт түрлі шешімі бар деп саналады.
Сонымен, егер есептің шарты кез-келген берілген фигураға қатысты қажетті фигураның белгілі бір орналасуын қамтамасыз етсе, онда толық шешім есептің шартын қанағаттандыратын барлық фигураларды тұрғызудан тұрады (егер мұндай фигуралар шектеулі санда болса).

1.3 Салу есебін шешу схемасы

Салу есебін шешудің белгілі бір схемасын таңдау туралы мәселе таза әдіснамалық сұрақ болып табылады.
Геометриялық есептің шешімі, мысалы, келесі схема бойынша жүзеге асырылса, өте жақсы болады:
1. Мәліметтерді таңдауда барлық мүмкіндіктерді пайдаланатын жағдайлардың шектеулі саны анықталды.
2. Әрбір жағдай үшін есептің шешімі бар ма және қанша деген сұраққа жауап беріледі.
3. Есептің шешімі болған әр жағдай үшін мүмкін шешімдердің әрқайсысын табудың (осы геометриялық құралдарды қолданудың) әдісі келтірілген немесе оны осы тәсілмен алуға болмайтындығы анықталған.
Бұл схема ғылыми мақалалар мен монографияларда басшылыққа алынады; дегенмен, бұл білім беру мақсаттарында, әсіресе орта мектеп жағдайында аз пайдаланады.
Әрбір күрделі салу есептерін шешкен кезде, мәселені шешудің жолын іздеу үшін, есептің барлық шешімдерін алу үшін, мәселені шешу мүмкіндігінің шарттарын білу үшін және тағы басқалар туралы сұрақ туындайды. Сондықтан, білім беру жағдайында сындарлы мәселелерді шешкен кезде, келесі төрт кезеңнен тұратын белгілі шешім схемасын қолданған жөн: 1) талдау; 2) салу; 3) дәлелдеме; 4) зерттеу.
Әрине, бұл схема өте қажет және өзгермейтін емес, оның жеке сатыларын қатаң түрде бөліп, оларды көрсетілген тәртіпте дәл жүргізу әрдайым ыңғайлы және мақсатқа сай емес. Бірақ бұл схема көбінесе дизайн мәселелерін шешуге көмектеседі. Осы схеманың әр кезеңін қарастырайық. [6-7].
1. Талдау. Бұл дайындық және сонымен бірге салу есебін шешудің ең маңызды кезеңі, өйткені мәселені шешудің кілтін өзі береді. Талдаудың мақсаты - қажетті пішіннің элементтері мен фигуралардың деректер элементтері арасында қажетті пішінді құруға мүмкіндік беретін осындай қатынастарды орнату. Бұған мәліметтер мен қажетті мәселелерді бейнелейтін эскиздік сурет салу арқылы проблеманың шарты талап ететін жерде қол жеткізуге болады. Бұл сызбаны қолмен жасауға болады. Кейде сызбаның салуы: Мәселе шешілді деп есептейік деген сөздермен бірге жүреді.
Көмекші сызбада осы элементтер мен табуға болатын маңызды элементтерді бөліп көрсету керек. Көмекші сызбаны құруды көбінесе осы суреттен емес, керекті фигураның жуық кескінінен бастап, оған есептерді шығаруда көрсетілген қатынастарда болатындай етіп деректерді қоса отырып бастаған жөн. Мысалы, егер сізге бір төбеден сызылған биссектрисасы, медианасы мен биіктігі бойынша үшбұрыш салу керек болса, онда анализде алдымен ерікті үшбұрыш салу, содан кейін онда есепте көрсетілген сызықтарды салу ыңғайлы.
Егер көмекші сызбада қажетті фигураны тұрғызудың тікелей әдісі ұсынылмаса, онда олар қажетті фигураның қандай да бір бөлігін немесе жалпы салуға болатын, содан кейін қажетті фигураны салуға болатын фигураны табуға тырысады. Жалпы жағдайда дәлелдеу келесідей. Қажетті фигураның салуы басқа фигураның салуына дейін азаятыны атап өтіледі. Сонда олар F формасының салуы F пішінінің салуына дейін азаятындығын байқайды және т.б. Шекті қадамдардан кейін салуы белгілі болған фигура санына келуге болады.
Мысалы, сіз табан бойымен және осы табанға тартылған медиана мен биіктік бойымен үшбұрыш салғыңыз келеді делік. Көмекші сызбаны қарастыра отырып, ABC үшбұрышы BDE үшбұрышы тұрғызылса, оны оңай құруға болатындығын ескереміз: содан кейін E нүктесінің екі жағында DE кесіндісінің жартысына тең сегменттерде шетке қалу ғана қалады. берілген негіз. Бірақ BDE үшбұрышы тіктөртбұрышты және гипотенузасы m мен h аяғының бойында тұрғызылған.
Талдауға көмектесетін келесі арнайы ескертулерді ескеру пайдалы.
1) егер көмекші сызбада мәліметтер мен шешуге қажетті элементтер арасындағы байланыстарды тікелей байқау мүмкін болмаса, онда сызбаға көмекші фигураларды енгізген жөн: бар нүктелерді түзулермен қосыңыз, қиылысты белгілеңіз қолданыстағы сызықтардың нүктелері, кейбір сегменттерді жалғастыру және т.б. Кейде бұрыннан бар түзулерге параллельдер немесе перпендикулярлар жүргізу пайдалы.
Мысалы, берілген А нүктесінен өтетін және берілген екі В және С нүктелерінен бірдей қашықтықта өтетін түзу сызық салу керек делік.

Сурет 1.13 - А нүктесі арқылы өтетін және В,С нүктелерінен бірдей
қашықтықта өтетін түзу

Сызбаны салуды - эскизді қажетті ізделінді фигурамен бастаған ыңғайлы: алдымен а түзуін саламыз, оның бойынан А нүктесін және а түзуінен бірдей қашықтықта, (түзудің қарама-қарсы жақтарында) В және С нүктелерін салып алайық. Сурет 1.13 көрсетілген.

Сурет 1.14 - А нүктесі арқылы өтетін және В,С нүктелерінен бірдей
қашықтықта өтетін түзу

Осыдан кейін, сызбада мәселені шешуге мүмкіндік беретін байланыстар әлі де пайда болмайды. ВВ1 және СС1 перпендикулярларын түзуге жүргізіп, ВС кесіндісін тұрғызып, ВС кесіндісінің а түзуімен қиылысуының М нүктесін белгілейік. М-дің BC сегментінің ортасы екенін байқау қиын емес, осыдан құрастыру әдісі қазірдің өзінде түсінікті. 1.14 суретте көрсетілген.
2) Егер есептің шарты бойынша кесінділердің немесе бұрыштардың қосындысы немесе айырмашылығы келтірілсе, онда бұл шамалар көмекші сызбада, егер олар ондайда болмаса, көрсетілуі керек.
3) Талдау жүргізу барысында теоремалар мен бұрын шешілген есептерді еске түсіру пайдалы, оларда қарастырылып отырған проблема жағдайында айтылғанға ұқсас элементтер арасында тәуелділіктер болады.
4) Белгілі бір сызбаны - эскизді зерттеуге негізделген талдау жасай отырып, біз белгілі бір дәрежеде өз ойымызды осы суретпен байланыстырамыз. Сонымен, 1) нүктесін бейнелейтін мысалда біз а түзуінің қарама-қарсы жағында В және С нүктелерін таңдадық, ал оларды осы түзудің бір жағында таңдау мүмкін болды. Біз талдау негізінде болатын шешім әдісі кейбір ерекше жағдайларда ғана қолайлы болып шығуы мүмкін. Біз алған шешім әдісі деректерді мейлінше кең таңдауға сәйкес келуі үшін қажетті фигураны мейлінше жалпы түрде бейнелеген жөн. Мысалы, қалаған үшбұрыш, егер есептер шығаруда оның пішінінің арнайы нұсқауы болмаса, жан-жақты, төртбұрыш ретсіз және т.б. Талдау барысында жалпы жағдайды талдайтын болсақ, болашақта мәселені толық шешуді жеңілдетеді.
Талдаудың тағы бір мысалын қарастырайық. Берілген үшбұрышқа шеңбер салу қажет.

Сурет 1.15 - Берілген үшбұрышқа іштей шеңбер салу

ABC берілген үшбұрыш болсын. Оған шеңбер салу үшін оның центрінің орнын анықтап, радиустың мәнін табу керек [5].
О нүктесі - іштей сызылған шеңбердің центрі, ал ОМ - шеңбердің үшбұрыштың бүйірлеріне жанасу нүктелерінің кез-келгенінде жүргізілген радиусты (мысалы, шеңбердің жанасу нүктесіне) елестетейік. жағы AB). Сонда ОМ кесіндісі АВ түзуіне перпендикуляр болады. Демек, ОМ - бұл сызылған шеңбер центрінің АВ үшбұрышының қабырғасынан қашықтығы. Шеңбердің барлық радиустары тең болғандықтан, шеңбердің центрі үшбұрыштың барлық жағынан бірдей қашықтықта орналасқан, сондықтан OA, OB және OS түзулер ABC үшбұрышының (ішкі) бұрыштарының биссектрисалары ретінде қызмет етеді. Бұл ойлар центрді тұрғызуға және қажетті шеңбердің радиусын анықтауға жеткілікті. 1.15 суретте көрсетілген.
2. Салу. Шешімнің бұл кезеңі қажетті фигураны салу үшін шығаруға жеткілікті болатын негізгі салулардың (немесе бұрын шешілген мәселелердің) реттілігін көрсетуден тұрады.
Салу, әдетте, салу үшін қабылданған құралдарды қолдана отырып, оның әр сатысының графикалық дизайнымен бірге жүреді.
Мысал ретінде берілген АВС үшбұрышына іштей сызылған шеңбер құру есебіне қайта оралайық. Осы есептің жоғарыдағы талдауы көрсеткендей, қажетті шеңберді тұрғызу үшін дәйекті түрде салу қажет:
1) осы үшбұрыштың кез-келген екі ішкі бұрышының биссектрисалары;
2) олардың қиылысу нүктесі О;
3) АВ түзуіне перпендикуляр О нүктесі арқылы өтетін түзу сызық;
4) сызылған перпендикулярдың М табаны;
5) шеңбер (О, ОМ).
3. Дәлелдеу. Дәлелдеудің мақсаты - құрастырылған фигураның проблемада қойылған барлық шарттарды шынымен қанағаттандыратындығын анықтау.

Сурет 1.16 - Берілген үшбұрышқа іштей шеңбер салу

Сонымен, берілген үшбұрышқа сызылған шеңбердің жоғарыда тұрғызылуының дұрыстығын дәлелдеу үшін, біз тұрғызған шеңбердің (О, ОМ) АВС үшбұрышының барлық қабырғаларына тиетіндігін орнату керек. Ол үшін, ең алдымен, АВ түзуінің сызылған шеңберге тиетіндігін байқаймыз, өйткені бұл түзу OM радиусына перпендикуляр[4-5].
Сонымен бірге шеңбердің радиусы оның центрінің берілген АВС үшбұрышының АВ қабырғасынан қашықтығына тең екендігі түсінікті. Әрі қарай, O шеңберінің центрі үшбұрыштың барлық жағынан бірдей қашықтықта орналасқанын ескереміз, өйткені ол үшбұрыштың бұрыштары биссектрисаларының қиылысында орналасқан. Демек, шеңбердің центрінің АС қабырғасынан немесе ВС қабырғасынан қашықтығы да салынған шеңбердің радиусына тең болады, сондықтан О мен АС және ВС үшбұрыштарының қабырғаларына перпендикулярлар жүргізсек, онда табандар осы перпендикулярлардың бірдей шеңберлерде орналасады.
Сонымен, AC және BC түзулерінің әрқайсысы шеңбердің бойында жатып, оның соңындағы сәйкес радиусқа перпендикуляр болады, демек, бұл түзулердің әрқайсысы салынған шеңберге тиіп кетеді.
Дәлелдеу, әдетте, салудың әр сатысы орындалуы мүмкін деген болжам бойынша жүзеге асырылады.
4. Зерттеу. Салу кезінде олар әдетте белгілі бір шешімді табумен шектеледі және салудың барлық сатылары шынымен де мүмкін деп болжануда. Мәселені толығымен шешу үшін сізге келесі сұрақтарды табу керек:
1) әрқашан мүмкін бола ма (яғни кез-келген мәліметтерді таңдау үшін), салуды таңдалған тәсілмен орындауға болады;
2) егер мүмкін әдісті қолдану мүмкін болмаса, мүмкін бе және қажетті фигураны қалай салу керек;
3) деректерді таңдаудың әр мүмкіндігінде қанша шешім бар.
Осы сұрақтардың барлығын қарастыру зерттеуді құрайды. Осылайша, зерттеу төлем қабілеттілігінің шарттарын құруға және шешімдер санын анықтауға бағытталған.
Кейде міндет те қойылады: қажетті фигураның қандай жағдайда немесе басқа қосымша талаптарды қанағаттандыратындығын білу. Мысалы, сұрақ туындауы мүмкін: қандай жағдайда қажетті үшбұрыш тік бұрышты немесе теңбұрышты болады? Немесе мұндай сұрақ: қандай жағдайда ізделген төртбұрыш параллелограмм немесе ромб болып шығады?
Көбіне мектеп оқушылары белгілі бір дәрежеде белгілі бір істерді таңдай отырып, зерттеу жүргізеді, және мұндай емес басқа жағдайлардың неге қаралатындығы түсініксіз. Сондай-ақ барлық мүмкін істердің қаралған-қаралмағандығы түсініксіз болып қалады. Кез-келген күрделі мәселенің шешімін зерттеу кезінде бұл тәсіл шешімдердің жоғалуына, кейбір жағдайлардың қаралмайтындығына әкелуі мүмкін.
Зерттеудің қажетті жоспарлауы мен толықтығына қол жеткізу үшін жол бойында зерттеу жүргізу ұсынылады. Бұл техниканың мәні салуды құрайтын барлық сатылар бойынша дәйектілікпен итерациялау және әр сатыға қатысты осы сатыда көрсетілген салудың әрқашан мүмкін болатындығын, егер мүмкін болса, қанша жолмен болатындығын анықтау болып табылады.
Бұл қажет:
1) шындықта әрдайым салудың жоспарланған салудың әр сатысында жасалуы керек нүктелер, сызықтар, шеңберлер немесе басқа фигуралар бар-жоғын біліңіз немесе олардың болуы позицияның ерекше таңдауына байланысты ма, жоқ па? белгілі бір фигуралардың мөлшері. Мысалы, егер шеңбердің түзу сызықпен қиылысу нүктелерін тұрғызу керек болса, онда мұндай нүктелердің болуы осы шеңбердің радиусы мен центрінің центрінің арақатынасына тәуелді екенін ескеру керек. түзу сызықтан шеңбер.
Әрі қарайғы зерттеулер тек салу салу мүмкін болған жағдайларда жүргізілуі керек, яғни. әр қадам іс жүзінде қажетті фигуралардың құрылуына әкелетін кезде.
2) шешім бар әрбір нақты жағдай үшін нақты қанша нүкте, сызық, шеңбер және т.б. салудың әр қадамын береді. Мысалы, егер шеңбер мен түзудің қиылысу нүктелері тұрғызылса, онда шеңбердің радиусы центрден түзу сызыққа дейінгі арақашықтықтан үлкен болса, ондай екі нүкте болатындығын ескеру керек, және егер шеңбердің радиусы центрдің түзу сызықтан қашықтығына тең болса.
3) Әрбір қадамды зерттеу нәтижелерін ескере отырып, мәселеге тұтастай жүгініп, бұл фигуралардың қандай жағдайда орналасуын немесе олардың қандай мөлшерде қатынасында есеп шынымен шешілетінін және қандай жағдайда шешілетінін анықтаңыз жоқ. Мүмкіндігінше, шешімділік шарттарын формула арқылы өрнектеңіз (теңсіздіктер немесе теңдіктер түрінде).
4) осы шешімдер бар мәліметтер туралы әр нақты болжам үшін мүмкін болатын шешімдердің санын анықтаңыз.
Осындай пайымдау нәтижесінде осылай салу мүмкіндігі туралы мәселе шешілді. Бірақ сұрақ әлі де ашық күйінде қалып отыр: егер салу тәсілі қандай да бір жолмен өзгертілсе, жаңа шешімдер пайда бола ма? Кейде берілген есептің кез-келген шешімі алынған шешімдердің бірімен сәйкес келетіндігін дәлелдеуге болады; бұл жағдайда зерттеу аяқталды деп санауға болады. Егер бұл сәтсіздікке ұшыраса, онда мәселенің басқа жолдары бар басқа шешімдері бар деп ойлауға болады. Бұл жағдайларда қайтадан талдауға жүгініп, деректердің орналасуының басқа ықтимал жағдайларының бар-жоғын немесе бұрын жүргізілген талдаумен көзделмеген қажетті цифрлардың бар-жоғын тексеру пайдалы болады.

2 САЛУ ЕСЕПТЕРІН ШЕШУДІҢ ӘДІСТЕРІ

Геометрияның бүкіл тарихы және математиканың кейбір басқа салалары геометриялық салулар теориясының дамуымен тығыз байланысты. Біздің дәуірге дейінгі 300 жыл шамасында ғылыми геометриялық жүйенің негізін қалаушы Евклид тұжырымдаған геометрияның ең маңызды аксиомалары геометриялық салулардың қандай рөл ойнағанын анық көрсетеді. Кез келген екі нүкте арқылы түзу жүргізуге сызық жүргізуге болады, Шектелген түзуді үздіксіз жалғастыруға болады, Кез келген нүктені центр етіп және де кез келген аралықты радиус етіп шеңбер жүргізуге болады - бұл Евклидтің постулаттары көне заман геометриясындағы конструктивті әдістердің негізгі позицияны ұстанғандығын анық көрсетеді [9-10].
Ежелгі грек математиктері шынайы геометриялық салуларды тек циркульмен және сызғышпен жасалған деп санады, салу есептерін шешудің басқа құралдарын заңды деп мойындамады. Сонымен қатар, Евклидтің постулаттарына сәйкес олар билеушіні шексіз және бір жақты деп санады, ал циркуль кез-келген радиустағы шеңбер салу қасиетіне жатқызылды. Циркульдермен және сызғышпен салуға арналған тапсырмалар әлі күнге дейін өте қызықты болып саналады және жүз жылдан астам уақыттан бері олар мектептің геометрия курсының дәстүрлі материалы болды.
Геометриялық салулар оқушының математикалық олимпиадалық дайындығында маңызды рөл атқаруы мүмкін. Есептердің бір де бір түрі оқушының математикалық және логикалық дағдыларын дамытуға геометриялық салулар есептері сияқты көп қырлы бола алмайды. Сонымен қатар, бұл есептер мектептегі геометрия курсының кез-келген бөлімінде оқушылардың теориялық білімдерін бекітуге ыңғайлы. Геометриялық салу есептерін шеше отырып, көптеген пайдалы дағдыларды қалыптастыруға болады.
Салу есептері дегеніміз - бұл қандай деректермен, фигура белгілі бір шарттарды қанағаттандыратындығын, қандай құралдармен қандай геометриялық фигураны салу керек екенін (жазықтықта сызу) білдіретін есеп.
Циркуль мен сызғышты пайдалану арқылы салу есептерін шешу оны алдын-ала мүмкін деп есептелетін бес қарапайым салу есептері жиынтығына дейін әкелуді білдіреді. Олар:
1. Егер екі А және В нүктелері салынса (берілсе), онда оларды қосатын АВ түзуі, сонымен қатар АВ кесіндісі және АВ және ВА сәулелерінің кез-келгені (сызғыш аксиомасы) салынады.
2. Егер О нүктесі мен АВ кесіндісі салынса, онда центрі О нүктесінде және радиусы АВ болатын шеңбер, сондай-ақ осы шеңбердің кез келген доғасы салынады.
3. Егер екі түзу салынса, онда олардың қиылысу нүктесі салынады (егер ол бар болса).
4. Егер түзу мен шеңбер салынса, онда олардың қиылысу нүктелерінің кез-келгені салынады (егер ол бар болса).
5. Егер екі шеңбер салынса, онда олардың кез-келген қиылысу нүктелері салынады (егер ол бар болса).
Әрбір есептің шешімін қарапайым салуларға дейін азайту шешуді ауыр етеді. Сондықтан есептің шешімі көбінесе негізгі салулар есебі есептеріне дейін келтіріледі. Кейбір салуларды негізгілері ретінде таңдау белгілі дәрежеде ерікті. Мысалы, келесі салуларды негізгі салулар ретінде қарастыруға болады: берілген бұрышты жартыға бөлу; берілгенге тең кесінді құру; берілгенге тең бұрыш құру; параллель түзу салу, перпендикуляр түзу салу, осыған байланысты кесінді бөлу; үш жағынан, екі жағынан және оған жанама жағынан және екі бұрышына үшбұрыш салу; гипотенуза мен катеттің бойымен тік бұрышты үшбұрыш салу.
Салу есептерін шешу үшін оның барлық шешімдерін табу керек.
Салу есебін шешудің белгілі бір схемасын таңдау туралы мәселе таза әдіснамалық сұрақ болып табылады.
Геометриялық есептің шешімін, мысалы, келесі схема бойынша жүзеге асыруға болады:
1. Мәліметтерді таңдауда барлық мүмкіндіктерді пайдаланатын жағдайлардың шектеулі саны анықталады;
2. Әрбір жағдай үшін есептің шешімі бар ма және қанша деген сұраққа жауап беріледі;
3. Есептің шешімі болған әр жағдай үшін мүмкін шешімдердің әрқайсысын табудың (осы геометриялық құралдарды қолданудың) әдісі келтірілген немесе оны осы тәсілмен алуға болмайтындығы анықталған.
Практикада салу есептерін шешу кезінде, келесі төрт кезеңнен тұратын схеманы қолданған жөн: 1) талдау; 2) салу; 3) дәлелдеу; 4) зерттеу.

2.1 Параллель көшіру әдісі

Көбінесе фигураны салу қиынға соғады, өйткені бұл фигураның бөліктері бір-бірінен тым алыс, сондықтан сызбаға мәліметтерді енгізу қиынға соғады. Бұл жағдайларда қажетті фигураның кез-келген бөлігі өзіне параллель немесе басқа жолмен беріледі, бірақ жаңадан алынған фигураны іздеудегі фигураға қарағанда тікелей немесе оңай құруға болатын қашықтықта болады. Мұндай тасымалдаудың бағыты мәселенің шартына байланысты және жаңадан алынған суретте мүмкіндігінше көп мәлімет болатындай етіп таңдалуы керек [11].
Мысал 2.1 Берілген қабырғалары бойынша трапецияны салу керек..
Шешуі.
1) Талдау. ABCD трапециясы салынсын: BC = a, AD = b, AB = c және де CD = d. СВ векторымен анықталған параллель көшіруді орындайық. Онда CD қабырғасы BD1-ге өтеді. АВD үшбұрышын c, d, b-a (ba) үш қабырғасы бойынша салуға болады.

Сурет 2.1 - Берілген қабырғалары бойынша трапеция салу

Содан кейін АD кесіндісін D D = a-ға жалғастырамыз. В нүктесі арқылы біз AD-ға параллель түзу сызық жүргіземіз және оған BC = a кесіндісін кейінге қалдырамыз. C және D нүктелерін қосайық. Алынған ABCD трапециясы - қалаған.
Салу жоспары айқын.
Дәлелдеуі. ABCD төртбұрышында AD параллель, сондықтан ABCD трапеция болып табылады, онда AB = c, AD = b, өйткені AD = b - a + a. BD = CD = d.
Зерттеу. ABD үшбұрышын үш қабырғасы бойынша салуға болады, егер
c - d b - a c + d. Бұл жағдайда барлық басқа салу қадамдары біржақты түрде жүзеге асырылады. Егер c - d b - a c + d теңсіздігі орындалмаса, онда таңдалған мәліметтер үшін есеп шешілмейді.
Мысал 2.2 Төртбұрышты оның бұрыштары мен қарама-қарсы қабырғаларын біле отырып салу керек.
Шешуі. Төртбұрыштың қабырғалары берілсін.

Сурет 2.2 - Берілген қабырғалары мен бұрыштары бойынша салу

Талдау. ABCD төртбұрышында BC және AD қабырғалары және A, B, C бұрыштары осы мәндерге ие болсын делік. BC-ді AE-ге өзімен параллель жылжытыңыз, сонда AE және AD екі қабырғалары белгілі болатын екі белгілі бұрыш пен айырымға тең EAD бұрышы, берілген BAD бұрышы мен берілгенге іргелес FBC бұрышы болатын AED үшбұрышы пайда болады. CBA. Мұндай үшбұрышты салу оңай. Содан кейін EC және CD сызықтарын салу оңай, өйткені біріншісі EA сызығымен белгілі бұрышты құрайды (CEG бұрышы FBC бұрышына тең); ал екіншісі AD жағымен белгілі CDA бұрышын құрайды. Осыдан кейін CB-ны EA-мен параллель жүргізу ғана қалады және шешім айқын.
Салу.
1. AED үшбұрышын салыңыз;
2. ЕО;
3. CD;
4. SV║EA.
Зерттеу.
Бұл есептің бір ғана шешімі бар: төртбұрыштың бұрыштары мен екі қарама-қарсы жақтарының қатынасы оның сыртқы түрін толығымен анықтайды.

2.2 Ұқсастық әдісі

Ұқсастық әдісінің негізгі идеясы:
Алдымен, берілген фигураға ұқсас, оның белгілі бір шарттарын қанағаттандыратын фигура салынады. Содан кейін ол ізделініп отырған суретке дейін ұқсастық салыпы, алынып тасталған талапты қанағаттандыратындай етіп толықтырылады.
Ұқсастық әдісі, әдетте, деректердің тек біреуі кесінді болған жағдайда қолданылады, ал қалған мәліметтер бұрыштар немесе кесінділердің қатынастары болып табылады.
Әдетте көмекші фигураны іздегенге ұқсас етіп алып қана қоймай, онымен бірге ұқсас орналасатындай етіп жасаған жөн. Бұл жағдайларда шешімнің жетістігі ұқсастық центрін таңдауға байланысты.
Ұқсастық әдісімен салу есептерін шешкен кезде келесі ескертуді жиі қолданадыз. Егер екі фигура ұқсас болса, онда ұқсастық коэффициенті кез келген сәйкес кесіндінің қатынасына тең болады. Егер Ф фигурасының a, b, c,... кесінділері ұқсас Ф1 фигурасының a1, b1, c1, ... кесінділеріне сәйкес келсе, онда ұқсастық коэффициенті де қатынастарға тең:
Мысал 2.3 АВС бұрышы және оның ішінде М нүктесі берліген. ВС кесіндісінен А нүктесінен және М нүктесінен бірдей қашықтықта орналасқан Х нүктесін табыңыз [12].

Сурет 2.3 - Мысал 2.3 есебінің сызбасы

Шешуі. Талдау. Перпендикуляр XY = MX болатындай етіп Х нүктесі табылсын. Есеп YXM фигурасын салуға келтіріледі. Қажетті пішінге ұқсас бірнеше кескінді елестетейік. Осы фигуралардың бірін салу жеткілікті, мысалы, PKN, өйткені М нүктесінен KR-ге параллель түзу жүргізу керек сонда есептің шешімі алынады.
PKN фигурасын салу үшін B - ізделініп отырған фигуралардың ұқсастығының центрі, сондықтан M, H, K және B нүктелері бірдей BMM және PN AB, PN = BN түзулерінде жатқанын, ал PN = BN екенін ескереміз. P нүктесі ерікті. Демек, PKN фигурасын салу үшін PN AB-ді ерікті P нүктесінде қалпына келтіру керек, ал N центрінен PN радиусын саламыз, К нүктесінде қиып өтетін доғаны саламыз. MX пен KN параллель салу арқылы қажетті X нүктесін аламыз.
Салуы.
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.