Жолды шығару функциялары

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

Alikhan Bokeikhan University

БАЯНДАМА

Ақпараттық технологиялар және экономика факультеті, ВТ-001 тобы
Орындаған: Омарғазы.Г.К.
Қабылдаған: Сагинтаев С. С.

Семей қаласы, 2021-2022 оқу жылы
Екілік таңбалар жолын сипаттаудың ішкі күрделілігі

ЖОСПАР

I. Кіріспе
II. Негізгі бөлім
Екілік таңбалар жолын сипаттаудың ішкі күрделілігі
Жолдармен жұмыс істеудің негізгі кітапханалық функциялары
IV. Қорытынды
V. Пайдаланылған әдебиеттер тізімі

КІРІСПЕ

Цифрлық құрылғыларда пайдаланылатын екілік санау жүйесі позициялық санау жүйесіне жатады. Демек, сандарды екілік санау жүйесінде көрсету үшін және оларға арифметикалық операциялар жүргізу үшін, өзімізге таныс, күнделікті пайдаланылатын ондық санау жүйесінің қағидалары пайдаланылады. Сондықтан, алда келтірілетін, екілік санау жүйесіне байланысты түсіндірмелер ондық санау жүйесіндегі сәйкесті мәселелерді еске түсіріп, салыстырма қарастырылым арқылы жүргізіледі.
Ондық санау жүйесінде сан жазуға он символ (0 ... 9) пайдаланылады (бұл жүйенің ондық санау жүйесі деп аталуы да осыған байланысты). Бұл символдардың сандағы тұрған орнына байланысты құны (салмағы) белгіленеді: ол онның (яғни, санау жүйесінің негізінің) сәйкесті разряд нөмірінің мәніндегі дәрежесі арқылы анықталады. Сонымен, санның ең кіші разрядындағы (нөлінші разрядтағы) символдың құны бір (100), келесі разрядтың (бірінші разрядтың) құны он (101), одан әрі жүз (102), мың (103) және с.с. өзгере береді. Разряд құны, мәніне сәйкесті, бірлік, ондық, жүздік, мыңдық деп және с.с. аталады, ал сан разрядында тұрған символ сәйкесті разряд құнының сан құрамына қанша рет кіретіндігін көрсетеді.

ЕКІЛІК ТАҢБАЛАР ЖОЛЫН СИПАТТАУДЫҢ ІШКІ КҮРДЕЛІЛІГІ

Ондық санау жүйесінде сан жазуға он символ (0 ... 9) пайдаланылады (бұл жүйенің ондық санау жүйесі деп аталуы да осыған байланысты). Бұл символдардың сандағы тұрған орнына байланысты құны (салмағы) белгіленеді: ол онның (яғни, санау жүйесінің негізінің) сәйкесті разряд нөмірінің мәніндегі дәрежесі арқылы анықталады. Сонымен, санның ең кіші разрядындағы (нөлінші разрядтағы) символдың құны бір (100), келесі разрядтың (бірінші разрядтың) құны он (101), одан әрі жүз (102), мың (103) және с.с. өзгере береді. Разряд құны, мәніне сәйкесті, бірлік, ондық, жүздік, мыңдық деп және с.с. аталады, ал сан разрядында тұрған символ сәйкесті разряд құнының сан құрамына қанша рет кіретіндігін көрсетеді. Келесі мысал арқылы айтылғанды түсіндірейік:

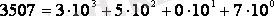
Сонымен, келтірілген санның құрамында 7 бірлік, 5 жүздік, 3 мыңдық бар, ал ондық жоқ (0).
Екілік санау жүйесінде сан жазуға екі символ (0 және 1) пайдаланылады. Разряд құны екінің (яғни, санау жүйесінің негізінің) сәйкесті разряд нөмірінің мәніндегі дәрежесі арқылы анықталады. Сонымен, санның ең кіші разрядындағы (нөлінші разрядтағы) символдың құны бір (20), келесі разрядтың (бірінші разрядтың) құны екі (21), одан әрі төрт (22), сегіз (23) және с.с. өзгере береді. Разряд құны бірлік, екілік, төрттік, сегіздік деп және с.с. аталады, ал екілік код разрядында тұрған символ сәйкесті разряд құнының сан құрамына қанша рет кіретіндігін, дәлірек айтқанда, бар-жоқтығын көрсетеді. Айтылғанды келесі мысал суреттейді:

Код құрамындағы символдардың 0 және 1 мәнінде ғана болуына байланысты, олар разрядқа сәйкесті құндық мәннің код құрамында бар-жоқтығын көрсетеді. Мысалы, келтірілген мысалдағы кодтың құрамында бірлік, екілік және сегіздік бар (1), ал төрттік жоқ (0).
1960 жылдары орыс математигі А.Н.Колмогоров: Екілік таңбалар тізбегін сипаттаудың ішкі күрделілігі қандай? Егер екілік жол тәуелсіз және тең үлестірілген кездейсоқ шамалардың тізбегі ретінде қарастырылса, онда оны сипаттау үшін бізге орташа реттік энтропияға тең бит саны қажет болады. Егер екілік таңбалар р екілік кеңеюінің бірінші миллион цифрларын құрайтын екілік цифрлар болса ше? Бұл жағдайда символдар жолы кездейсоқ болып көрінеді, бірақ оны қарапайым компьютерлік бағдарламаның көмегімен алуға болады. Сондықтан, егер біз осындай жолдың миллиондаған биттерін компьютер бар басқа жерге жібергіміз келсе, біз екілік таңбалардың орнына бағдарламаны жіберіп, компьютерден миллиондаған биттерді сол жерде шығаруды сұрай аламыз. Осылайша, р -ның миллион бит кеңейтілуін сипаттаудың күрделілігі өте аз.
Осындай ойларға сүйене отырып, А.Н.Колмогоров екілік жолдың күрделілігін осы жолды құруға қабілетті жалпы мақсаттағы компьютер үшін ең қысқа бағдарламаның ұзындығы деп анықтады. (Бұл күрделілік идеясын Г. Чайтин мен Р. Соломонов дербес және бір мезгілде ұсынды.)
Жалпы мақсаттағы компьютерді кез келген басқа компьютерді модельдей алатын Тьюринг машинасы деп санауға болады. Бір қарағанда, А.Н.Колмогоров ұсынған күрделіліктің анықтамасы пайдасыз болып көрінеді, себебі бұл белгілі бір компьютердің мүмкіндіктеріне байланысты. Бірақ бұл олай емес, өйткені кез келген жалпы мақсаттағы компьютер кез келген басқа жалпы мақсаттағы компьютерді модельдей алады, содан кейін бір компьютерге жазылған кез келген бағдарламаны ұзындығы тұрақты имитациялық бағдарламаның префиксі арқылы басқа компьютердің бағдарламасына түрлендіруге болады. Осы идеяға сүйене отырып, күрделілік шамасы компьютерге тәуелсіз екенін көрсетуге болады. Кез келген объектіні сипаттаудың күрделілігі компьютерге немесе объектіні сипаттайтын адамға байланысты емес. Белгілі бір болжамдар бойынша, Колмогоровтың күрделілігі Шеннонның энтропиясынан басқа ештеңе емес екенін дәлелдеуге болады. Басқаша айтқанда, орта есеппен кездейсоқ объектіні қайта шығаруға қабілетті ең қысқа компьютерлік бағдарламаның ұзындығы осы объект шығарылған ықтималдылықты бөлудің энтропиясына тең. Колмогоров күрделілігі деректерді қысу мәселелеріне бірыңғай көзқарасты ұсынады. Сонымен қатар, ол статистикалық тұжырымдама теориясының негізі ретінде қызмет етеді (Оккам ұстарасы: Ең қарапайым түсіндіру - ең жақсы) және есептелу теориясымен тығыз байланысты.

ЖОЛДАРМЕН ЖҰМЫС ІСТЕУДІҢ НЕГІЗГІ
КІТАПХАНАЛЫҚ ФУНКЦИЯЛАРЫ

1, ., 0 а, б - символдар
01 рррр мектеп ... - сөздер
Паскалда символдар тізбегін жол литер строка дейді. Сөздермен, символдармен жұмыс істейтін шамаларды жолдық немесе литерлік шамалар д.а. Паскалда жеке таңбаның типі CHAR деп аталды. Ал, жолдың типі STRING д.а.
chr(x) - x коды бойынша таңбаны анықтайды.
Char - айнымалының мәні жеке символ болатынын білдіретін тип,
String - айнымалының мәні сөзсөйлем екенін білдіретін тип, мәндегі символдар саны 256-дан аспауы керек.
Text - мәтіндік тип, файл аттарын белгілеуде қолданылады.
Компьютердегі барлық таңбаны коды бшы басып шығаратын программа жазыңыз:
ord(sh) - sh таңбасының ASC кодын анықтайды.
Program kody;
Var i:integer;
Begin
I:=0;
Repeat
Writeln(I,' `,chr(i));
I:=i+1;
Until i255;
End.
program kody2;
var tanba:char;
label 10,20,30;
begin
10:Write(`таңба енгізіңіз `);
Read(tanba);
If tanba='0' then goto 20;
Writeln(tanba,' `,ord(tanba));
goto 10;
20:End.

2. Символдармен жұмыста жиі қолданылатын стандартты функциялар.
Атауы
Процедура немесе функция
Шаманың типі
әрекеті
Chr(x)
функция
x - integer
Х санын сиволға түрлендіреді
Odd(x)
функция
x - integer
=True,егер х -тақ, =False х -жұп болса
Inc(x)
процедура
x - реттік
X-ті 1-ге арттырады
Dec(x)
процедура
x - реттік
X-ті 1-ге кемітеді
Inc(x,n)
процедура
x - реттік, n - бүтін
X-ті n-ге арттырады
Dec(x,n)
процедура
x - реттік, n - бүтін
X-ті n-ге кемітеді
Random(x)
функция
x - integer
0 мен x-1 аралғынан кездейсоқ сан табады
Random
функция

(0..1) аралғынан кездейсоқ сан табады
3. Мәтінмен сөз-сөйлем жұмыста жиі қолданылатын функциялармен процедуралар.
program a_sanau;
uses crt;
var i,n,k: integer;
s: string;
begin
write('tanbalar tizbegin engiz, ');
read(s);
n:=length(s); k:=0;
for i:=1 to n do
if (s[i]='а') or (s[i]='a') then k:=k+1;
writeln('sozdegi kichi "a"-lar sany - ',k);
end.
С) Оқулықтағы 121 беттегі 14 жаттығу;
нұсқау: 0 мен 9 арасындағы сандардың АSC-кодтары 47- 59 аралығында жатады.

program sanemes;
var i,n:integer;
s:string;
begin
write('tanbalar tizbegin engiz, ');
read(s);
n:=length(s);
for i:=1 to n do
if ((ord(s[i]))47) and ((ord(s[i]))59)
then writeln(s[i],' ','san') else writeln(s[i],' ','san emes');
readln;
end.

Жолдармен жұмыс істеу әр түрлі тапсырмаларға байланысты қиын болуы мүмкін. Мысалы, жолды түйе тәрізді қарапайым түрлендіру үшін бірнеше код жолдары қажет болады:
function camelize(str) {
return str.replace((?:^\w[A-Z]\b\w\s+) g, function(match, index) {
if (+match === 0) re
turn ""; не if (\s+.test(match)) пробел
return index === 0 ? match.toLowerCase() : match.toUpperCase();
});
}
Бірақ егер мұндай сызықтар әлі де өңделуі керек болса ше? Сіз бұл мысалды түзете аласыз немесе арнайы кітапханаларды қолдануға жүгіне аласыз. Олар күрделі алгоритмдерді енгізуді жеңілдетеді, сонымен қатар, жоғарыда келтірілген мысалға қарағанда, әлдеқайда икемді және әмбебап бағдарламашының құралдарын береді. Бұл қиын тапсырманы шешу үшін сізге тек бір әдісті шақыру қажет болуы мүмкін.
Жолдармен жұмыс істеу үшін бірнеше JavaScript кітапханалары туралы сөйлесейік.
String.js
String.js кітапханасы, немесе жай ғана S - браузерде және Node.js. -те пайдалануға болатын шағын (қысылған және қысылған 5 КБ -тан аз) JavaScript кітапханасы. Ол программистке жолдармен жұмыс істеу әдістерінің кең спектрін ұсынады. Бұл string.js нысанының әдістері, олар ыңғайлы болу үшін стандартты жол әдістерін қамтиды. String.js нысаны қалыпты жолдар үшін орауышқа ұқсайды.
Бағдарламада жолдарды келесідей анықтауға болады:
жолдың тұрақтылары ретінде;
символдар жиыны ретінде;
көрсеткіш арқылы символ түріне;
жолдардың жиымы ретінде.
Сонымен қатар, жолды сақтау үшін жад бөлу болуы керек.
Қос тырнақшаға алынған таңбалардың кез келген тізбегі жол тұрақтысы ретінде қарастырылады.
Дұрыс шығару үшін кез келген жол нөлдік таңбамен аяқталуы керек '\ 0', бүтін мәні 0. Жолдың тұрақты мәнін жариялау кезінде оған автоматты түрде бос таңба қосылады. Сонымен, жолдың тұрақтысы болып табылатын символдар тізбегі компьютердің жедел жадында орналасады, оның ішінде нөлдік байт.
Жолды сақтау үшін тізбектелген жад ұяшықтары бөлінеді. Осылайша, жол символдар жиыны болып табылады. Жолдағы әр таңбаның кодын сақтау үшін 1 байт бөлінеді.
Кейбір қызметтік таңбаларды жол тұрақтысына орналастыру үшін символдық комбинациялар қолданылады. Сонымен, егер сіз жолға қос тырнақшаны енгізгіңіз келсе, оның алдында кері қиғаш сызық болуы керек: '\' '.
Жолдық тұрақтылар статикалық жадыда бөлінеді. Қос тырнақшалардағы таңбалар тізбегінің бастапқы адресі жолдық адрес ретінде қарастырылады. Жол тұрақтылары көбінесе printf () сияқты функциялармен пайдаланушымен байланысу үшін қолданылады.
Символдар массивін анықтау кезінде ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.