Stud.kz

Арифметикалық прогрессия


Жұмыс түрі:  Реферат
Тегін:  Антиплагиат
Көлемі: 6 бет
Таңдаулыға:   

7-лекция

Сандық тізбек және прогрнессиялар тақырыбыен оқып-үйрену

Жоспары:

1. Сан тізбегі.

2. Арифметикалық прогрессия

3. Геометриялық прогрессия.

Әдебиеттер:

1. Рахымбек Д. А рифметика, алгебра, анализ бастамаларын оқыту әдістемесі. /Оқулық/ - Шымкент: М. Әуезов атындағы ОҚМУ баспа орталығы 2016. - 432 б

2. Елубаев С. Математиканы оқыту әдістемесі. - Алматы; Эверо, 2016

3. Мектеп оқулықтары

4. Мұғалімге арналған оқу-әдістемелік құралдар

1. Сан тізбегі тізбектің берілу тәсілдері. Рекуренттік формула .

Орта мектепте прогрессиялар - тiзбек ұғымына байланысты оқытылады.

Анықтама. Белгiлi бiр заңмен немесе ережемен бiрiнен соң бiрi келiп отыратын сандардың жиынын сан тiзбегi деп атайды.

Мысалы:

1, 2, 3, . . . , n , . . . (натурал сандар тiзбегi) ;

2, 4, 6, . . . , 2 n , . . . (жұп сандар тiзбегi) ;

1, 3, 5, . . . , 2 n +1, . . . (тақ сандар тiзбегi) ;

2, 3, 5, 7, 11, 13, . . . (жай сандар тiзбегi) .

Тiзбектi құратын әрбiр санды оның мүшелерi делінеді. Сан тiзбегi математикада жалпы түрде былайша жазылады:

а 1 , а 2 , . . . , а n , . . . (1)

а n -дi (1) тiзбектiң жалпы мүшесi деп атайды.

Бұдан кейiн өспелi және кемiмелi тiзбектер және тiзбектiң берiлу тәсiлдерi қарастырылады.

Тiзбек көбiнесе тiзбектiң n -шi мүшесiнiң формуласы арқылы берiледi. Мысалы, жұп оң сандардың тiзбегi а п =2n.

Тiзбек кейде рекурренттiк тәсiлмен берiлуi мүмкiн.

Тiзбектiң қандай да бiр мүшесiнен бастап, кез келген мүшесiн алдыңғы мүшелерi арқылы өрнектейтiн формуланы рекурренттiк формула деп атайды (латынның recurro - қайта оралу деген сөзiнен шыққан) .

Мысалы: а 1 =3, а п +1 = а п 2 .

Бұл тiзбектiң мүшелерiн былайша жазып көрсетуге болады:

3, 9, 81, . . . , . . .

Бұдан кейiнгi сабақта арифметикалық прогрессияның анықтамасы берiледi.

6. 1. 1 Арифметикалық прогрессия

Анықтама. Екiншi мүшесiнен бастап әрбiр мүшесi өзiнiң алдындағы мүшеге бiрдей санды қосқанға тең болатын тiзбек арифметикалық тiзбек деп аталады.

Басқаша айтқанда кез келген натурал п сан үшiн а n+1 =а п +d (мұндағы d - қандай да бiр сан) шарты орындалса, онда ( а п ) тiзбегi арифметикалық прогрессия болады.

d=а п+1 -а п -ны арифметикалық прогрессияның айырмасы деп атайды. d >0 болғанда арифметикалық прогрессияны өспелi, ал d< 0 болғанда арифметикалық прогрессияны кемiмелi деп атайды. Арифметикалық прогрессияны былайша белгiлейдi:

а 1 , а 2 , . . . , а n , . . . немесе а n+1 =а п +d.

Арифметикалық прогрессияның анықтамасы бойынша

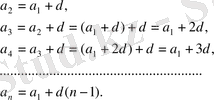
Демек, арифметикалық прогрессияның n-шi мүшесiнiң формуласы мынаған тең:

a n =а 1 +d(п-1)

Бұл формуланың дұрыстығы математикалық индукция әдiсiмен дәлелденiледi.

Арифметикалық прогрессияның п -шi мүшесiнiң 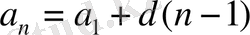формуласын басқаша 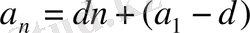түрiнде жазуға болады. Бұдан кез келген арифметикалық прогрессияны 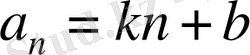(мұндағы k мен b -қандай да бiр сандар) түрiндегi формуламен беруге болады.

Керiсiнше де тура болады: 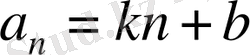түрiндегi формуламен берiлген ( а п ) тiзбегi арифметикалық прогрессия болып табылады (мұндағы k мен b -қандай да бiр сандар) .

Сондықтан да арифметикалық прогрессияны натурал сандар жиынында анықталган функция деп қарастыруға болады.

Арифметикалық прогрессияға ғана тән қасиет былайша дәлелденiледi:

Арифметикалық прогрессияның анықтамасы бойынша

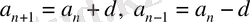
бұдан

.

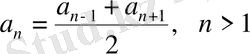Сонымен, арифметикалық прогрессияның екiншi мүшесiнен бастап әрбiр мүшесi оның екi көршiлес тұрған мүшелерiнiң арифметикалық ортасы болып табылады. Егер арифметикалық прогрессияның бiрiншi мүшесi мен айырымы а 1 және d белгiлi болса, онда оның қалған мүшелерiн 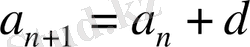рекурренттiк формуласы арқылы шығарып алуға болады.

Арифметикалық прогрессияның алғашқы n мүшесiнiң қосындысы мына формуламен анықталады:

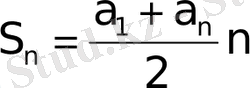(1)

Бұл формуланы арифметикалық прогрессияның n-шi мүшесiнiң формуласы дейдi. а п =а 1 +d(п-1) болатындықтан, (1) формуланы мына түрде жазуға болады:

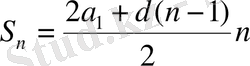(2)

6. 1. 2 Геометриялық прогрессияны оқыту

Анықтама. Екiншiсiнен бастап әрбiр мүшесi өзiнiң алдындағы көршiлес мүшенi бiрдей санға көбейткенде шыққан нөлден өзгеше сандардың тiзбегi геометриялық прогрессия деп аталады.

Басқаша айтқанда, кез келген натурал n үшiн 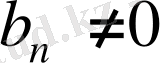және 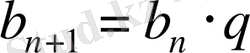(мұндағы q -қандай да бiр сан) шарттары орындалса, ( b n ) тiзбегi геометриялық прогрессия болады.

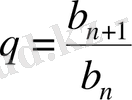санын геометриялық прогрессияның еселiгi деп атайды.

Индукция әдiсiмен геометриялық прогрессияның n-шi мүшесiнiң мына формуламен анықталатындығы көрсетiледi.

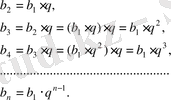
Бұл формуланың дұрыстығы математикалық индукция әдiсiмен дәлелденедi.

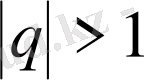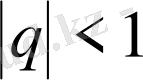болғанда геометриялық прогрессияны өспелi , ал болғанда геометриялық прогрессияны кемiмелi деп атайды.

Геометриялық прогрессияға ғана тән қасиет былайша дәлелденiледi: геометриялық прогрессияның анықтамасы бойынша 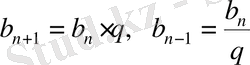, бұдан .

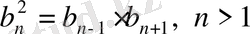Егер геометриялық прогрессияның мүшелерi оң болса, онда 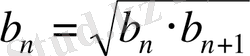екiншi мүшесiнен бастап геометриялық прогрессияның әрбiр мүшесi көршiлес екi мүшесiнiң геометриялық ортасына тең болады.

Геометриялық прогрессияны былайша белгiлейдi:

.

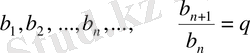( b п ) геометриялық прогрессия берiлген болсын. Оның алғашқы п мүшесiнiң қосындысын S п арқылы өрнектеймiз:

S п =b 1 +b 2 +b 3 + . . . +b п-1 +b п (1)

Бұл теңдiктiң екi бөлiгiн де q -ге көбейтемiз:

S п ⋅q=b 1 ⋅q +b 2 ⋅q +b 3 ⋅q + . . . +b п-1 ⋅q +b п ⋅q

Егер

b 1 ⋅q= b 2 , b 2 ⋅q= b 3 , …, b п-1 ⋅q=b п

екенiн ескерсек:

S п ⋅q=b 2 +b 3 + . . . +b п +b п ⋅q (2)

(2) теңдiктен (1) теңдiктi мүшелеп шегерiп, ұқсас мүшелердi бiрiктiрейiк:

S п ⋅q-S п =(b 2 +b 3 + . . . +b п +b п ⋅q) -(b 1 +b 2 +b 3 + . . . +b п-1 +b п ) =b n ⋅q-b 1

Ендi 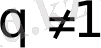дейiк. Онда

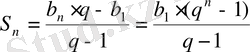(3)

формуласы келiп шығады.

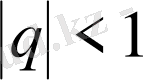болғанда шектеусiз геометриялық прогрессияның қосындысы былайша анықталады:

Прогрессияның алғашқы n мүшесiнiң қосындысының формуласын жазамыз:

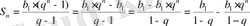(4)

Егер 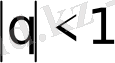болса, онда да 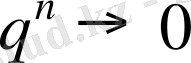, сондықтан да 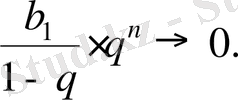(4) формуланың бiрiншi қосылғышы п- ге тәуелсiз. Демек, да, 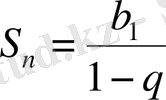-қа ұмтылады.

Сонымен, шексiз кемiмелi геометриялық прогрессияның қосындысы мына формуламен анықталады:

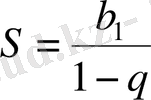(5)

Шексiз кемiмелi геометриялық прогрессияның қосындысының формуласын ондық бөлшектердi жай бөлшектерге айналдыруда қолдануға болады.

0, (5) таза периодты ондық бөлшегiн мына түрде жазуға болатындығы белгiлi:

... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар
Талдау мектеп оқулықтары және материалдар ҰБТ осы тақырып бойынша Арифметикалық және геометриялық прогрессиялар
Арифметикалық және геометриялық прогрессиялар
Логарифмдік өрнектерді есептеу әдістері
Жай сандардан құрылған арифметикалық прогрессиялар
Арифметикалық прогрессияның анықтамасы
Арифметикалық прогрессия туралы
Арифметикалық және геометриялық прогрессия туралы
ПРОГРЕССИЯНЫҢ ҚОСЫНДЫЛАРЫН ЕСЕПТЕУДЕ ГЕОМЕТРИЯЛЫҚ ӘДІСТЕРІН ҚОЛДАНУ
Стандарттарды мемлекеттік қадағалау
Математика сабағында көрнекі құралдарының қолдануының психология- педагогикалық негіздері
Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

google play appstore

instagram tiktok

Ақпарат

Қосымша


Email: info@stud.kz



Реферат Курстық жұмыс Диплом Материал Диссертация Практика Презентация Сабақ жоспары Мақал-мәтелдер 1‑10 бет 11‑20 бет 21‑30 бет 31‑60 бет 61+ бет Негізгі Бет саны Қосымша Іздеу Ештеңе табылмады :( Соңғы қаралған жұмыстар Қаралған жұмыстар табылмады Тапсырыс Антиплагиат Қаралған жұмыстар kz