ЕВКЛИДТЕН БҰРЫНҒЫ ГЕОМЕТРИЯ

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 168 бет
Таңдаулыға:

Мазмұны

Кіріспе . . .

Математикалық құрылымдар және евклидтік емес геометриялар . . . Математикалық структура ұғымының мәні . . . Геометрияның алғашқы ұғымдары . . . Евклид және оның геометриясы . . .
Бесінші постулат және оны дәлелдеу әдістері . . . Бесінші постулатқа эквивалентті (мәндес) ұйғарымдар . . . Бесінші постулат проблемасы және оны дәлелдеу әдістері . . . Бесінші постулат проблемасының шешілуі . . . Евклидтік емес геометрияның ашылуы . . . Лобачевский және оның геометриясы. Лобаческий аксиомасы . . .
Гильберт аксиомалар жүйесіне шолу . . . Д. Гильберттің «Геометрия негіздері» . . . І- топ. Тиістілік аксиомалары . . . ІІ-топ. Реттілік аксиомалары . . . ІІІ-топ. Конгруэнттілік аксиомалары . . . ІV-V-топтар. Үздіксіздік және паралельдік аксиомалары . . .
Вейль аксиомалар жүйесі . . . Үш өлшемдік Евклидтік кеңістіктің Вейль аксиомалар жүйесі . . . Векторлық кеңістіктің аксиомалары . . . Вейль аксиомалар жүйесінің қайшылықсыздығы . . . Вейль аксиомалар жүйесінің тәуелсіздігі . . . Вейль аксиомалар жүйесінің толықтығы . . . Вейль аксиомалар жүйесінде негізгі геометриялық ұғымдарды анықтау . . . Вейль аксиомалар жүйесінде кейбір теоремаларды дәлелдеу . . .
Мектеп геометриясының аксиомалар жүйесі . . . Колмогоровтың геометриялық аксиомалар жүйесі . . . Погореловтың геометриялық аксиомалар жүйесі . . . А. Д. Александровтың геометриясының аксиомалар жүйесі . . . Л. С. Атанасянның геометриясының аксиомалар жүйесі . . . Мектеп курсы геометриясының логика-аксиоматикалық құрылымы . . .
Лобачевский аксиомасы мен түзулердің паралельдігі. Лобачевский жазықтығындағы үшбұрыштар мен төртбұрыштар . . . Лобачевскийдің аксиомасы . . . Лобачевский бойынша түзулердің паралельдігі . . . Паралельдік бұрышы . . . Лобачевский жазықтығындағы үшбұрыштар мен төртбұрыштар . . .
Парлель және ажырасатын түзулер . . . Паралель түзулердің өз-ара орналасулары . . . Ажырасатын түзулердің қасиеттері . . .
Лобачевский жазықтығындағы кейбір сызықтар . . . Түзулер шоғы . . . Тең көлбеулі қиюшылар . . . Жазықтықтағы сызықтар . . .
Лобачевский кеңістігіндегі түзулер, жазықтықтар мен беттер туралы . . . Түзулер мен жазықтықтар және олардың өзара орналасуы . . . Лобачевский кеңістігіндегі беттер . . .
Лобачевский планиметриясының қайшылықсыздығы, паралельдік аксиомаларының тәуелсіздігі. Лобачевский жазықтығының кейбір интериретациясы . . . Пуанкаре интерпретациясы . . . Кэли-Клейн интерпретациясы . . .
Евклидтік геометрияларға қысқаша шолу . . . Сфералық геометрияның негізгі ұғымдары . . . Риманның эллипстік геометриясы . . .
Вейль схемасындағы Лобачевскийдің гиперболалық геометриясы . . . Псевдоевклидттік кеңістіктер . . . Гиперболалық кеңістіктер . . . Аксиомалар жүйесінің қайшылықсыздығы . . . Кэли-Клейннің проективтік моделі . . .
Геометриялық шамаларды өлшеу . . . Кесінділерді өлшеу. Кесінді ұзындығы, оның бар болуымен жалғыздығы . . . Көпбұрыштың ауданы . . . Тең шамалы және тең құрамды көпбұрыштар . . . Көлем теориясы . . .

Кіріспе

«Геометрия негіздері» пәнінен ұсынылып отырған оқу құралында геометрияның логика-аксиоматикалық негіздері және евклидттік емес геометрияларды зерттеу әдістері қарастырылады. Оқу құралында математикалық құрылым ретінде евклидттік геометрияның Гильберт және Вейль бойынша теориялық негіздемелері қарастырылған. Евклидттік емес геометриялардың математикалық құрылымдары мен олардың интерпретациялары келтірілген.

Геометрия негіздері пәнінің ең таңдаулы тарауларының бірі Лобачевский геометриясының логикалық құрылымы мен модельдері зерттелген.

Геометрияның негізгі бөлімдерінің бірі «өлшеулер теориясы» егжей тегжейлі қарастырылып, мектеп геометриясының оқулықтарына шолу жасалды.

«Геометрия негіздері» пәні жоғарға геометрияның ең негізгі бөлімдерінің бірі болып табылады. Бұл пән келешек математика пәні мұғалімдері үшін ең қажетті пәндердің бірі болып табылады.

Оқу құралы автордың көп жылдардын бері оқыған лекциялары және орыс тіліндегі [1, 2] оқу құралдары негізінде құрастырылған.

Бұл оқу қрылымы физика-математика мамандығының студенттеріне және жоғары геометрия пәнін оқитын студенттер мен оқытушылар үшінкөмекші құрал ретінде пайдалы болады деп санаймыз.

Осы оқу құралының электрондық нұсқасы қашықтықтан оқитын студенттерге де өте қажет болады.

1. Математикалық құрылымдар және евклидтік емес геометриялар

1. 1 Математикалық құрылым ұғымының мәні

Кез келген А жиын берілген болсын. Осы жиында бір немесе бірнеше қатынастарды анықтау және сол қатынас(қатынастар) орындалатын шарттарды (аксиомаларды) беру мүмкін. Бұл жағдайда А жиында структура анықталған дейміз. Сонан соң берілген аксиомалардан структураның кейбір қасиеттерін келтіріп шығару мүмкін. Бұл қасиеттер, әдетте, лемма, теоремалар түрінде баяндалады. Структураны кеңірек үйрену нәтижесі оны сипаттайтын ерекшеліктерін ашу мүмкіндігін береді. Структураға тиісті мәліметтерді белгілі бір системаға салу, яғни үйреніп отырған структураның теориясын жарату мүмкін. Бұл теория А жиындағы структураның аксиоматикалық теориясы болады. А жиынның элементтерінің табиғаты мұнда ешқандай роль атқармайды.

«Математикалық құрылым» ұғымын қалыптастыру әлемді танудың маңызды ғылыми құралы - аксиоматикалық әдістің дамуымен байланысты. Мәселе мынада, қазіргі кезде осы күнгі математиканың көптеген бағыттары тек қана аксиоматикалық әдістің, яғни, сәйкес аксиомалар жүйесінің /аксиоматика/ негізінде құрылады. Ал математика ғылымының әр саласына тән аксиомалардың өзі ұзақ және күрделі тарихи даму процесінде пайда болды. Бастапқы мәліметтер адамның практикалық қызметінің нәтижесінде жинақталады, қордаланады. Осындай мағлұматтарды тексереді, нақтылайды, жүйелейді және басқадай бастапқы мәліметтерден шығарып алу мүмкін болатындары олардың ішінен алынып тасталады. Кейде, қалған қарапайым

мәліметтер /аксиома/ тізімінің толық еместігі байқалады, яғни бұл мәліметтер барлық теоремаларды қорытуға жеткілікті бола алмайды. Мұндай жағдайда бұл тізімге жетпей тұрған аксиомалар қосылады. Нәтижесінде аксиомалардың толық жиынтығы /аксиоматика/ қалыптасады. Осындай аксиоматика жүйесі негізінде қазіргі математиканың ондаған бағыттары дамуда, олардың қатарына: қарапайым /элементар/ математиканың аксиоматикасы, натурал санның аксиоматикасы, метрикалық және векторлық кеңістіктің аксиоматикасы, сан өрісінің аксиоматикасы, группаның аксиоматикасы, ықтималдықтар теориясының аксиоматикасы, математикалық құрылымдардың аксиоматикасы және басқалар жатады.

Егер кез келген жиын элементтерінің арасында тұжырымдардың /аксиомалардың/ белгілі жүйесімен сипатталатын қандай да қатынас анықталса немесе операция тағайындалса, онда осы бір жиында математикалық құрылым анықталған дейді.

«Құрылым» ұғымының басты ерекшелігі - табиғаты әр алуан болатын жиын элементтеріне оның жарамды болатындығында және де қарастырылатын қатынастар /немесе операциялар/ сипатының таңдалу тұрғысынан жоғары дәрежеге ие екендігінде.

Сондықтан белгілі аксиомалардың жиынтығымен қандай да бір жиын элементтері ие болатын қатынастар мен операциялардың мәнді қасиеттері сипатталады.

Шексіз көп әралуан құрылымдар бар және олардың жиынтығын белгілі бір ретпен оқу, зерттеу математиканың әр түрлі бөлімдерінің мазмұнын құрайды. Бұл қазіргі математиканы құрастыруға, яғни оны аксиоматикалық әдіспен құрылымдардың жүйесі ретінде көрсетіп берудің мүмкіндігін білдіреді.

Математикалық құрылымдардың типі және олардың сипаттамасы

Математика ғылымында «құрылым» терминін енгізген Н. Бурбаки барлық математиканың іргетасын құрайтын бірнеше негізгі құрылымдарды ғана анықтады.

Нақтырақ айтқанда, олар бір-біріне келтірілмейтін құрылымдардың үш типін: алгебралық құрылымдарды, реттік құрылымдарды, топологиялық құрылымдарды анықтады /дегенмен, Бурбакилердің өздері негізгі құрылымдардың саны түпкілікті анықталды деп есептемейді/.

Математикалық құрылымдар аксиоматикасының мән-мағынасына тереңдемей, құрылымдардың негізгі типтерін жалпы түрде ғана қарастырайық.

Алгебралық құрылым

а/ Жиындардың тобын, яғни әр алуан сипаттағы элементтерден және онда анықталған операциялардан құралған әр түрлі жиындарды қарастырайық. Әрбір жиынды құрайтын элементтердің табиғатына назар аудармай, осы қарастырып отырған топқа енетін кез-келген жиынды А={х, у, z, . . . } символымен белгілейік. А жиынында анықталатын операцияны f арқылы белгілейік. А жиынына тиісті кез-келген х және у элементтері үшін осы жиыннан сәйкес операцияның нәтижесі болатын z элементі табылады, яғни

z=f (х, у)

Осында қарастырылатын жиындардың әрқайсысында анықталған операциялардың барлығы үшін ақиқат болатын жалпы қасиеттерді бөліп көрсетейік.

Коммутативтік: =f (у, х)

Ассоциативтік: 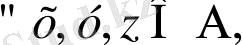f (f (х, у), z) = f (х, f (у, z ) )

Қайтымдылық: f (х, у) = у

Жалпы түрде өрнектеліп көрсетілген осындай үш қасиетті негізгі аксиомалар ретінде қабылдап, осы аксиомалар жүйесінен қарастырылып отырған жиындар тобына енетін /А, f/ жиынының кез-келгені үшін ақиқат болып табылатын басқа да салдарлар мен теориялық тұжырымдарды қорытып шығаруға болады.

Жоғарыда қарастырылған қасиеттермен /аксиомалармен/ сипатталатын /А, f/ жиынын коммутативтік топтың құрылымымен жабдықталған дейді. Осындай группаның құрылымы алгебралық типтегі құрылымның мысалы бола алады.

Анықтама: А жиында берілген қатынас А дағы екі элемент арқылы үшінші элементті бір текті(қалыпты) анықтаса, әдетте мұндай қатынас композиция заңы деп аталады.

Анықтама: Егер структура анықтамасындағы қатынас композиция заңынан тұрса, мұндай структура алгебралық структура деп аталады.

А жиында анықталған композиция заңы(бинарлық амал) әртүрлі болуы мүмкін. * амал А дағы бекітілген бір композиция заңы болсын. Сонда * амал А жиында алгебралық структура (А, *) ны анықтады дейміз. А жиында анықталған түрлі композиция заңдары түрлі алгебралық структураларға алып келеді.

Алгебралық құрылымға мыналар жатады: топтар, сақина, өріс, Булл структурасы, т. с. с.

Реттік құрылым

б/ Алдыңғы жағдайдағыдай қандай да бір жиындардың тобын қарастырайық және бұған енетін әрбір жиын элементтерінің арасында қатынастар анықталсын.

Өткен жағдайға ұқсас қарастырылатын жиындар тобына тиісті кез-келген жиынды А={х, у, z, . . . } символымен, ал онда анықталатын қатынасты - Р символымен белгілейік. Осындай жиындардың әрқайсысында анықталған қатынастар үшін ақиқат болып табылатын жалпы қасиеттерді бөліп көрсетейік.

1. Рефлексивтік:

2. Антисимметриялық:

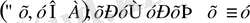
3. Транзитивтік:

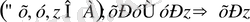
Бастапқы аксиомалар ретінде осы үш қасиетті қабылдап барлық тұжырымдарды жиындар тобына енетін кез келген /А, Р/ жиыны үшін де сәйкес қағидалар ақиқат болып табылатын жалпы теория құруға болады. Жоғарыда қарастырылған қасиеттермен /аксиомалармен/ сипатталатын /А, Р/ жиынын қатаң емес реттік құрылымымен жабдықталған дейді. Бұл құрылым реттік типтегі құрылымның мысалы бола алады.

Анықтама: Егер кез келген А жиында 1-3 аксиомаларды қанағаттандыратын Р қатынас берілген болса, оны А жиында реттік структура анықталған деп атайды.

Мысалдар келтірейік: 1) Нақты сандар R жиынында «үлкен», «кіші», қатынастары 1-3 аксиомаларды қанағаттандырады, сондықтан да олар реттік структураға мысал болады. Яғни, (R, үлкен), (R, кіші) структуралар реттік структуралар.

Топологиялық құрылым

в/ Қандай-да жиындардың тобын алайық. Осы жиындар тобына енетін әрбір жиынынан ішкі жиындардың тобын бөліп алайық.

Қарастырылатын жиындар тобының кез-келген жиынын Р, ал оған сәйкес қандай да ішкі жиындардың тобын 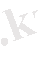Q арқылы белгілесек, онда оларға тән келесі жалпы қасиеттерді тұжырымдауға болады:

Мұндай фильтрлеуші жиынның құрылымын анықтайтын Q жиыны, Р жиынының фильтрі деп аталады. Фильтрлеуші жиынның құрылымы құрылымның топологиялық типінің мысалы бола алады.

Математиканың «архитектурасы»

Іргетасын жоғарыдағыда айтқандай негізгі құрылымдар құрайтын, математиканы ары қарай түзу, конструкциялау екі негізгі тәсілмен іске асады: әртүрлі құрылымдардан түзілген күрделі құрылым құрастыру арқылы; қандайда негізгі құрылымның аксиомаларына бір немесе бірнеше толықтама аксиомалар қосу барысында пайда болатын арнаулы математикалық құрылым құрастыру арқылы жүзеге асырылады.

«Күрделі» құрылымның жеке мысалы ретінде коммутативтік сызықтық-реттелген топтың құрылымын, ал «арнаулы» құрылым ретінде- сызықтық реттік құрылымды алуға болады.

Күрделі құрылымның жасалуы математиканың бүкіл бір бөлімінің, ал арнаулы құрылымның түзілуі қандайда жалпы теориядан бөлінген әр түрлі өзінше дамитын теорияның (математика бөлімдерінің) пайда болуына алып келеді.

Математиканың қандай да бір бөлімін( мысалы, натурал сандар ұғымына анықтама болатын Пеано аксиомасы құрудың аксиоматикалық әдісін қарастырайық:

1 . Құрастырылатын бөлім шеңберінде анықталмайтын (яғни анықтамасыз қабылданатын) алғашқы терминдер деп аталатын, саны шектеулі ұғымдар мен олардың арасындағы қатынастар іріктеледі;

2. Бастапқы ұғымдар мен қатынастардың өзара байланысын тағайындайтын және оларды жанама түрде анықтайтын ақиқаттығы дәлелдеусіз қабылданатын бірнеше бастапқы тұжырымдар-аксиомалар алынады;

3. Қарастырылатын бөлімге енгізілетін барлық жаңа ұғымдар бастапқы терминдер немесе бұрын анықталған мен қатынастар арқылы анықталады, ал бөлімнің барлық жаңа тұжырымдары (терминдері) дедукциялық жолмен алғашқы терминдердің немесе аксиомалардың (немесе бұрын дәлелденген теоремалардың) негізінде дәлелденеді және де қорытып шығару ережесі (ақиқат сөйлемнің бірі екінші бір ақиқат сөйлемнен туындайды) беріледі және ол математикалық логикада зерттеледі;

4. Аксиоматикалық теорияны нақты объектілер жиынында жүзеге асыру үшін аксиоматикалық теорияның көрнекі көрсетіліп берілуі (немесе модулі) пайдаланылады.

Аксиоматикалық әдіс

Қандайда бір математикалық теорияны аксиоматикалық әдіспен анықтау үшін, алдымен ол теория қарастыратын объектілер және олардың арасындағы қатыстар анықталады. Ол объектілер мен қатыстарды бұл теорияның негізгі ұғымдары дейді. Математикада бір ұғымға анықтама беру үшін бұрын анықталған басқа ұғымдарды пайдаланады. Сонан соң бірқатар ұғымдар топтамасы анықтамасыз алынып, солардың жәрдемімен басқа ұғымдарды анықтауға тура келеді. Анықтамасыз алынатын бұл ұғымдармен қатар бірқатар тұжырымдарды дәлелсіз алады. Ол тұжырымдар бұл теорияның аксиомалары делінеді. Ол аксиомалар алынған негізгі ұғымдар арасындағы қатыстарды сипаттайды.

Әрине, анықтамасыз алынатын ұғымдар(аксиомалар) қалауынша алына бермейді. Олар белгілі бір шарттарға, талаптарға сай болады. Атап айтқанда аксиомалар жүйесі -қайшылықсыз, тәуелсіз және толық (жеткілікті) болуы керек.

Алынған ұғымдар мен олар арасындағы қатыстар және аксиомалар тізімі теория басында келтіріледі. Солардың жәрдемімен жаңа ұғымдар анықталып теоремалар тұжырымдалып, олар дәлелденеді.

Математикада аксиоматикалық(дедуктивтік) әдістің жаратылуына грек ғалымдарынан Пифагор, Аристотель, Платон, Евклид т. с. с. лар бастапқы қадам қойған. Бұл салада әсіресе, Евклидтің (Б. Э. Д. 340-287ж. ж. ) қызметі үлкен болған. Евклид «Негіздер» (Бастамалар) деп атаған еңбегінде геометрияның логикалық құрылымын негіздеу мақсатында алдын ала анықтамалар келтіріп, кейін аксиомалар, постулаттар системасын қабылдады. Осылай ол өз заманының талабына сай геометрия «скелетін» құрды.

Аксиоматикалық әдістің мағынасын дұрыс түсіну мақсатында орта мектепте үйренілетін геометрия курсына назар аударайық. Мұнда бірнеше теоремалар дәлелденген болып, дәлелденген әрбір теорема өзінен алдын келген теоремаларға негізделеді, сол сияқты, жұмыста дәлелсіз қабылдау үшін қажет болған пікірлер және ұғымдарды кездестіреміз: нәтижеде анықтамасыз қабылданған объекттер ( мысалы, нүкте, түзу, жазықтық, ара қашықтық) оларды байланыстыратын қатыстар (мысалы, нүктенің түзу бойында орналасуы, түзудегі кез келген нүктенің сол түзудегі басқа екі нүктенің «арасында» орналасуы, кесінді және бұрыштардың тең (конгруэнт) тігі) пайда болады.

Негізгі объекттер, оларды байланыстыратын қатыстар және тиісті аксиомалар системасын таңдап алу өтә жауапты мәселе. Аксиоматикалық әдіс негізінде ой қорытуды қысқаша былайша сипаттау мүмкін: Бастапқыда анықталмайтын негізгі объекттер таңдап алынады, кейін оларды өзара байланыстыратын негізгі қатынастар-аксиомалар системасы таңдалады, сонан соң осы аксиомалар негізінде логика заңдылықтарына негізделген жағдайда жаңа-жаңа сөйлемдер (теоремалар) дәлелденеді.

Аксиомалар системасына қойылатын талаптар

Кез келген математикалық теорияның негізі ретінде алынған, қабылданған аксиомалар системасы мынадай талаптарға жауап беруі тиіс:

логика заңдылықтары бойынша аксиомалар системасынан бірін -бірі терістейтін екі сөйлем келіп шықпайтын болсын, яғни аксиомалар системасы қайшылықсыз болсын;
аксиомалар системасында қатысқан әрбір аксиома қалғандарының логикалық қорытындысы болмауы -теорема түрінде дәлелденбеуі тиіс, яғни аксиомалар системасындағы әрбір аксиома тәуелсіз болуы керек;
аксиомалар системасы қатарына осы системадан логикалық тұрғыда келіп шықпайтын жаңа аксиоманы қосу мүмкін бе, яғни аксиомалар системасы толық(кемелденгендік) қасиетіне мойынсынама ? Осы сұраққа жауап беретін болуы керек, яғни толық (кемелденген) аксиомаларға негізделеді.

Геометрияны аксиоматикалық құруға тиісті бұл сұрауларға 19 ғасырда толық жауап табылды. Бұл сұрауға жауап беруде ұлы орыс математигі Н. И. Лобачевский шығармашылығы және 19 ғасыр ғалымдарынан Е. Бельтрами, А. Пуанкаре, Ф. Клейн зерттеулері шешуші рол атқарды. Аксиомалардың белгілі системасы негізінде жүргізілетін тұжырымдардың қарама-қайшылыққа алып келу немесе келмеуі мәселесін шешуде математикада модель (интерпретация, сараптау) идеясы қолданылады.

Анықтама: Белгілі объекттердің жиындарының бірі анықталған болып, сол жиын элементтері арасында негізгі қатынастар( қатыстар) сақталып, мұнда аксиомалардың барлық шарттары орындалса, бұл аксиомалар системасының моделі құрылған деп аталады.

Мысалдар келтірейік. 1-мысал. Бүтін сандар жиыны қосу амалына сәйкес, группа (топ) құратыны үшін, бұл жиын группа аксиомалары системасының моделі бола алады (мұнда негізгі объекттер бүтін сандар болып, негізгі қатынас қосу амалы болады) .

2-мысал. Жазықтықтағы барлық геометриялық векторлар жиыны сызықтық кеңістік аксиомалары системасының моделі болады (мұнда негізгі объект геометриялық вектор болып, негізгі қатынастар векторларға қолданылатын сызықтық амалдар-қосу, векторды сан(скаляр) ға көбейту)

Анықтама: Аксиомалар системасынан бірін-бірі терісттейтін екі тұжырым келіп шықпайтын болса, бұл система қайшылықсыз( қарама-қарсы емес) система деп аталады. Керісінше, аксиомалар системасы қайшылықты система деп аталады.

Математикада қайшылықты системалармен жұмыс жүргізілмейді. Аксиомалар системасының қайшылықсыздығы қалай дәлелденеді?

Аксиомалар системасының қайшылықсыздығы осы система моделінің таңдап алынуына байланысты шешіледі. Егер тексерілетін аксиомалар тізімі берілген моделде орындалатындығы әйтеуір бір тәсілмен шешілсе және бұл модель объекттердің табиғатында қайшылыққа ұшырамаса, онда аксиомалардан бірін-бірі логикалық терістейтін екі тұжырым келіп шықпайтындығы, яғни бірде-бір фактты әрі дәлелдеп, әрі терістеп болмайтындығы белгілі болады. Мұны аксиомалардың қайшылықсыздығын дәлелдеу жолы дейміз.

Анықтама: Қайшылықсыз аксиомалар системасында әрбір аксиома сол системадағы қалған барлық аксиомалардың логикалық қорытындысы болмаса, мұндай аксиомалар системасы тәуелсіз система деп аталады.

Олай болса, аксиомалар системасының тәуелсіз болу талабы әрбір аксиоманың қалған аксиомалардың қорытындысы(нәтижесі, салдары) еместігін тексерумен дәлелденеді. Бұл мәселе төмендегідей шешіледі.

Аксиомалардың қайшылықсыз А ₁ , А ₂ , . . . , А _п системасына тиісті, мысалы, А _п аксиоманың тәуелсіз екендігін көрсету үшін бұл системадан А _п ді шығарып тастап, оның орнына А _п ^__ аксиома, яғни А _п нің мазмұнын терістейтін тұжырым енгізіп, аксиомалардың жаңа системасын құрастыру және оның қайшылықсыз екендігін дәлелдеу керек.

Аксиомалар системасының бір аксиомасының тәуелсіздігі, яғни оның өзбетінше аксиома екендігі бұл системадағы аксиомалар санын кемейту мүмкін еместігін білдіреді.

Аксиомалар системасының толықтылығының мазмұны мыналарды білдіреді, яғни аксиомалар қоспай осы теорияға тиісті әрбір дауды осы системаға сүйеніп оның орындылығын немесе теріскейін айту мүмкін болсын. Бұл талаптың орындалуы әдетте система үшін құрылған екі модель арасындағы изоморфизм деп аталатын ұғымға негізделеді.

Анықтама: Аксиомалар системасының екі Е, Е ¹ моделінің негізгі объектті (нүкте, түзу, жазықтық) арасында өзара біртекті сәйкестік орнатылған болып, бұл сәйкестікте элементтер(объект) екі моделде де біртүрлі қатынаста болса, яғни, А Е=А ¹ Е ¹ болса, бұл екі модель изоиорф деп аталады.

Анықтама. Аксиомалар системасына тиісті кез келген тұжырымдардың дұрыс немесе дұрыс еместігін анықтау мүмкін болса, аксиомалардың бұл системасы толық (кемелденген) деп аталады.

Аксиомалардың қайшылықсыз С(сумма) системасы берілген болсын, осы система негізінде құрылған теорияның барлық тұжырымдарын үш сыныпқа жіктеу мүмкін:

С(сумма) және одан логикалық тұрғыда келіп шығатын қорытындылар жәрдемінде дәлелдеу мүмкін болған тұжырымдар.
С(сумма) және одан логикалық тұрғыда келіп шығатын қорытындылар жәрдемінде терістеу мүмкін болған тұжырымдар.
С(сумма) және одан логикалық тұрғыда келіп шығатын қорытындылар жәрдемінде дәлелдепте және терістепте болмайтын\ мүмкін болған тұжырымдар.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.