Архимед денелері

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 16 бет
Таңдаулыға:

Т.Шонанұлы атындағы жалпы білім беретін орта мектебі

ЖОБА

Тақырыбы: Архимед денелері
Дайындаған: Елемесқызы Жангүлім

Ғылыми жобаның мақсаты: Архимедтік денелердің маңызды қасиеттерін, басқа да ұсыныстарды зерттеу.
Ғылыми жұмыстың гипотезасы: Күрделі денелердің жайылымын бірнеше түрде беруге болады. Архимедтік денелердің жайылымдарында симметриялық қатаң сақталатындықтан математикада әртүрлі әмбебап денелерді, оларды ұтымды орналастыруды қарастыру кезінде графтарды қолдану жұмысты едәуір жеңілдететін болады.
Тақырыптың өзектілігі: Қазіргі уақытта архимедтік денелердің графтық қасиеттері көп зерттелмегеннен кейін олардың оңай тәсілмен жайылуы, сандарын ескере отырып олардағы эйлерлік және гамильтондық айналулардың бар болуы ,болса олардың саны туралы зерттеулер көп сұраныс тауып отыр.
Тақырыптың жаңашылдығы: Лакольді және қарапайым жолдардың көмегімен жартылай дұрыс полиэдрлардың құрылымы есептеледі, дұрыс полиэдрлардың ұтымды жазылу алгоритмі берілді. Күрделі денелердің жайылымын бірнеше түрде беруге болады.
Зерттеу кезеңдері: Зерттеу жұмысында қажетті теоремалар мен түсініктері беріледі, осы теоремалары қолданылып. Әрбір дененің өзіне тән қасиетін қарастыра келе Эйлерлік мінездемесі табылып, қарпайым дененелерден күрделі денелерді алудың оңай тәсілдері көрсетілді.

Мазмұны
І.Кіріспе
ІІ.Негізгі бөлім
1. Архимед-ерте заман данышпан ғалымы
2. Архимедтік денелер
3..Басқа жасанды денелер.
4.Доп пен цилиндр теоремасы
ІІІ.Қорытынды
6.Пайдаланылған әдебиеттер тізімі

Кіріспе
Қазіргі уақытта архимедтік денелердің графтық қасиеттері көп зерттелмегеннен кейін олардың оңай тәсілмен жайылуы, сандарын ескере отырып олардағы эйлерлік және гамильтондық айналулардың бар болуы ,болса олардың саны туралы зерттеулер көп сұраныс тауып отыр.Платондық және Архимедтік денелердің жайылымдарында симметриалық қатаң сақталатындықтан математикада, информатикада әртүрлі әмбебап денелерді, оларды ұтымды орналастыруды қарастыру кезінде оларды қолданысы жұмысты едәуір жеңілдететін болады.
Зерттеу жұмысында қажетті теоремалар мен түсініктері беріледі.Осы теоремалары қолданылып Платон денелерінің жайылымдары құрылады.Әрбір дененің өзіне тән қасиетін қарастыра келе Эйлерлік мінездемесі табылып, қарпайым дененелерден күрделі денелерді алудың оңай тәсілдері көрсетілді.
Осы күрделі денелердің жайылымын бірнеше түрде беруге болатыны тұжырымдалып, жайылымы жасалып, сызбада көрсетілді. Локальді және қарапайым жолдардың көмегімен жартылай дұрыс полиэдрлардың құрылымы есептеледі, дұрыс полиэдрлардың ұтымды жазылу алгоритмі берілді.
Көпжақтылар-жазық көпбұрыштардың (полигонның) жиынтығы.
Кез келген полигонның төбесі полиэдр төбесі деп аталады, ал оның жағы полиэдрдің қабырғасы, полигоның өзі-полиэдрдің жағы деп аталады.
Полиэдр-дөңес, егер ол өзінің кез-келген жағының жазықтығының тек бір жағында жатса. Дөңес полиэдрдің ең негізгі ерекшелігі, оның эйлерлік мінездемесінің екіге тең болатындығында: Ɛ(Р)=n-m+g=2, бұл жерде n-төбелер саны, m-қабылғалар саны, g-жақтар саны.
Дұрыс полиэдр-барлық жақтары тең дұрыс полигондар болатын дөңес полиэдр. Оның әр төбесіне бірдей қабырғалар саны сай келеді. Дұрыс полиэдрдің тек бес түрі бар: Дөңес полиэдрлардан басқа, дөңес емес дұрыс полиэдрлардың Кеплер-Пуансо ашқан төрт түрі бар.

2.Архимедтік денелер

Жақтары әр түрлі бірнеше көпжақтар, ал көпжақты бұрыштарды өз ара тең болған көпжақтар жартылай дұрыс немесе архимедтік көпбұрыштар деп аталады. Архимед бес түрлі дұрыс көпжақтардан, басқа он үш түрлі жартылай дұрыс көпжақтар болатындығын тапты олар архимедтік денелер деп аталады. Дұрыс көпжақтар көп зерттелді, сол зерттеу нәтижелерінің бірі Л.Эйлердің мына теоремасы: Дөңес дұрыс көпжақтардың төбелері мен жақтары сандарының қосындысынан қырлары санын шегерілгендегі қалдық екіге тең.
Т+Ж-Қ=2
Т-төбе саны, Ж-жақ саны, Қ-қыры саны
Куб пен паралелепипедтте
8төбе+6жақ-12қыр=2
Үшбұрыш пирамида
4төбе+4жақ-6қыр=2
Октаэдр
6төбе+8жақ-12қыр=2

1.Қиық тетраэдр- тетраэдрді төрт төбесінен төрт жазықтықпен қиған кездегі пайда болған фигура. n=12, m=18, g=8.Ал эйлерлік мінездемесі Ɛ(Р)=n-m+g=2.Онда төрт үшбұрышты, төрт алтыбұрышты жақтар бар.Оның екі түрлі жайылымы бар:үшбұрышта және гексагонда

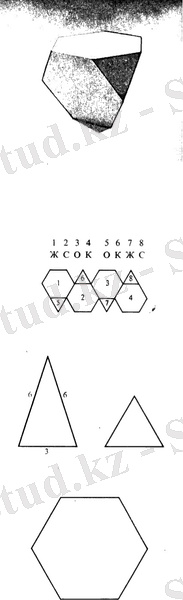
Қиылған тетраэдр қатты денелер, яғни жартылай қырлы дөңес полиэдрлер тұқымдасына жатады. Тетраэдрді тетраэдрден шыңдарды кесу арқылы алуға болады. Кесу процесінде тетраэдрдің беттері тұрақты алтыбұрышқа айналады, ал жойылған шыңдардың орнына квадрат беттер қарама-қарсы алты бұрыштыға параллель болып көрінеді.
Кесілген тетраэдрді салу әдісі карталарды бояу принципін қанағаттандыратын керемет бояуды көрсетеді. Алты қырлы беттер бастапқы тетраэдрдің беттерімен бірдей түсті алады; әр квадрат бет қарама-қарсы алтыбұрышты бетпен бірдей түсті алады
Кесілген тетраэдрді тұрғызу үшін қалған үш алтыбұрыш пен үш үшбұрышты алтыбұрыштың біріне кезекпен жапсыр. Енді бөліктерді біріктіріңіз және сізде үшбұрышты тесік бар модель бар. Саңылауды соңғы үшбұрышты бетпен жабыңыз.

2. Қиық октаэдр- оның төбелерін сегіз басқа қиюшы жазықтықтармен қиған кезде пайда болатын фигура. n=24, m=36, g=14.Ал эйлерлік мінездемесі Ɛ(Р)=n-m+g=2.Төменде оның шаршы жақты жайылымы берілген:

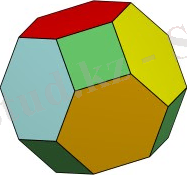
Қиық октаэдр және оның шаршыдағы жайылымы төбелері алмастырулардан тұратын көпжақ.
Оның төбелерінің саны S4 жиынынан алынған алмастыру 4!=24-ке тең. Sn={f:N--N;N={1,2,...n}}
Sn - n алмастырулар жиыны,ол универсал симметриалы жиын құрайды.Мұнда қиық октаэдрдің кез-келген екі алмастыруларға сәйкестендірілген төбелері іргелес болады,егер бір-біріне тек көршілес транспозиция (i,i+1) арқылы көшірілсе.Мұнда сол жақ (i1,i2) транспозицияны L арқылы, ортаңғы (i2,i3) транспозицияны M арқылы,оң жақ (i3,i4) транспозицияны R арқылы белгіледік.Қиық октаэдрдің әр төбесінен транспозициялары L, M, R болатын үш қабырға шығатынын ескерсек және қиық октаэдрдің квадраттарының
L және R, ал гексагонда L (R) М-мен кезектеседі.

Қиық октаэдрдің суреті көптеген басылымдарда эмблема түрінде кездеседі.Атап айтқанда,PFA Дискреттік матеметика журналының эмблемасы.Мұның мәнісі қиық октаэдр - S4 тобының остов тобы (4- ретті симметриялы топ)-4 элементтен тұратын 24 алмастыру.Мұның өзінде Sn универсам топтың тривиалды емес қасиеті бар.

3.Қиық гексаэдр: n[]=24, m[]=36, g[]=14, Ɛ(Р)=n-m+g=2.Сонымен қатар,кубтың алты шаршы жақтары қиылу кезінде алты сегізбұрышқа(октагон),ал оның сегіз төбесі сегіз үшбұрышқа айналады.Оның жайылымын кубтың жайылымындағы төбелердің орнына үшбұрыштарды қою арқылы алуға болады.

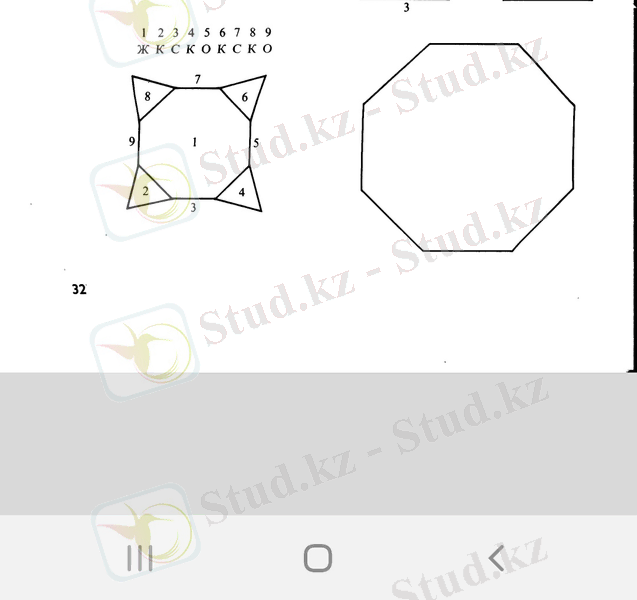
4.Қиық додекаэдр: n[]=60, m[]=90, g[]=32. Ɛ(Р)=n-m+g=2.Жиырма үшбұрышты жақ,он екі онбұрышты жағы болады.Жазбасы додекаэдрдің жазбасындағы төбелерді үшбұрыштармен алмастырғанда шығатын фигура болып табылады.

Қиық додекаэдр қатты денелерден тұратын архимед тұқымдасына, яғни дөңес дөңес полиэдрлерге жатады. Қысқартылған додекаэдрді додекаэдрден шыңдарды кесу арқылы алуға болады. Кесу процесінде додекаэдрдің беттері тұрақты декагонға айналады, ал алыстағы шыңдардың орнына үшбұрыштар пайда болады.
Карталардың боялу принципін қанағаттандыратын бояуды декодонды беттердің боялуын додекаэдрдің бір бояғышынан көшіру және үшбұрышты беттерге жаңа түсті таңдау арқылы алуға болады.
Үшбұрышты және онбұрышты беттермен кезекпен бастапқы декагонды қоршаңыз. Іргелес декагондарды желімдеу. Үшбұрышты тесіктерді әлі жаппаңыз. Көршілес декагондардың арасына келесі бес ондықты жапсырыңыз, және оларға өз кезегінде соңғы, соңғы декагонды жабыстырыңыз. Үшбұрышты тесіктерді пайдаланып, жапсырмаларды ішкі жағынан жақсы пинцетпен ұстаңыз. Енді басқа модельдер сияқты үшбұрышты қақпақтармен тесіктерді жабу қалады.

5.Қиық икосаэдр.n[]=60,m[]=90,g[]=32.Ɛ( Р)=n-m+g=2.Барлық үшбұрышты жақтар алтыбұрыштарға, ал төбелері бесбұрыштарға айналады.Ол икосаэдр тобының остовы болып табылады.Икосаэдр алгебрадағы бесінші дәрежелі теңдеулерді шешуде маңызды рөл атқарады.Икосаэдр және оның теңдеулерін шешу туралы лекциялар,қиық икосаэдр фирмалық футбол доптарының моделімен түсіндіріледі.

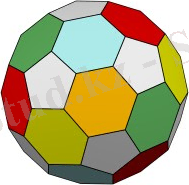
Қысқартылған икосаэдр қатты денелер, яғни жартылай қырлы дөңес полиэдрлер тұқымдасына жатады. Кесілген икосаэдрді икосаэдрден шыңдарды кесу арқылы алуға болады. Кесу процесінде икосаэдрдің беттері тұрақты алтыбұрышқа айналады, ал жойылған шыңдардың орнында тұрақты бесбұрыштар пайда болады.

Карталардың бояу принципін қанағаттандыратын бояуды алты қырлы беттердің боялуын икозэдрдің бір бояғышынан көшіру арқылы, ал бесбұрышты беттер үшін жаңа түсті таңдау арқылы алуға болады.

Бастапқы бесбұрышқа бес алтыбұрышты желімдеуден бастаңыз. Алтыбұрышпен сақина салуды жалғастырыңыз, әр орталыққа бесбұрыш қосыңыз. Нәтижесінде әрбір алтыбұрыш осындай үш сақинаға енеді.

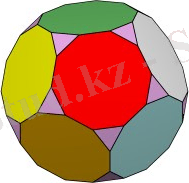
6.Кубооктаэдр.Кубооктаэдр- төбелері куб жақтарының орталары болатын қималар арқылы пайда болады.Оның құрамында алты шаршы,сегіз үшбұрыш бар. n=12,m=24,g=14. Ɛ(Р)=n-m+g=2.Оның ең айқындалған қасиетіне оның төртінші дәрежелі тұрақты граф екендігі жатады.Графтың аты оның куб пен октаэдрге жақындығын көрсетеді:Центрлері бір нүктеде қиылысатын және октаэдрдің диагоналі кубтың жақтарына перпендикуляр болатындай қиылысқан куб пен октаэдр - кубооктаэдрді құрайды.Кубооктаэдрдің құрылысын түсіндірудің ең оңай жолы:Кубтың әр жағына төбелері кубтың қырларының ортасында жататын іштей квадрат саламыз.Кубооктоэдр графы- планарлы және оның екі түрлі жайылымы бар:квадраттаңы және үшбұрыштағы.Кубооктаэдрдің ең негізгі қасиеті:оның екі түрлі жақтары болады:квадрат ,үшбұрыш.Және бір типті жақтың көршілері екінші типті болады.

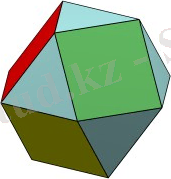
7.Қиық кубооктаэдр - кубооктаэдрдің төбелерін жазықтықтармен қиған кезде пайда болатын фигура.

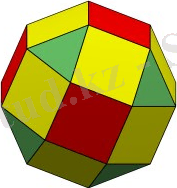
8.Икосододекаэдр - икосаэдр мен додекаэдрдің қиылысуынан пайда болған фигура,сондықтан,онда үшбұрышты он екі жақ,пентагондық он екі жақ бар.
2. Қиық икосододекаэдр - жазықтықтары үш типті болатын көпжақ.

9.Қиық икосододекаэдр - жүз жиырмасыншы тізбектегі планарлы кубтық гамильтондық граф.n=120,m=180,g=62.Ɛ(Р)=n-m+g=2.

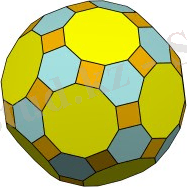Ромбо-кесілген icosidodecahedron қатты денелер архимед тұқымдасына, яғни дөңес дөңес полиграндарға жатады. Ол ромбойкозидодекаэдрден гөрі басқа ромбтық қысқартылған икозидодекаэдрден алынған. Бұл полиэдр қарапайым түс береді - додекаэдрден қалған барлық декагондар бір түске боялған, октаэдрдан қалған алтыбұрыштар - екіншісінде, ромбтық шыққан квадраттар - үшінші.

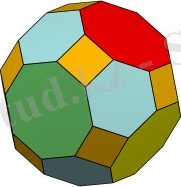
10.Ромбокубооктаэдр.Бұл көпжақтың он сегіз жағы квадрат,сегіз жағы үшбұрыш болып табылады.Оны шеткі жақтары квадрат болатын октапризма мен квадраттар мен үшбұрыштардан құралған симметриялы сегізбұрыштының қосылуы арқылы елестетуге болады.

11.Ромбоикосододекаэдр - n=60,m=120,g=62 болатын алпысыншы тізбектегі төртінші дәрежелі жоспарланған граф.

12.Қисық куб - n=24,m=60,g=38 болатын жиырма төртінші тізбектегі бесінші дәрежелі тұрақты планарлы граф болып табылады.
Архимед қатты ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.