Түйіндес оператор

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

М. Х. ДУЛАТИ АТЫНДАҒЫ ТАРАЗ ӨҢІРЛІК УНИВЕРСИТЕТІ

«ҰСТАЗ» ИНСТИТУТЫ

Кафедра _ Математика _

КУРСТЫҚ ЖҰМЫС

Пәні: Функционалды анализ

Тақырыбы: Гильберттік кеңістіктегі өзіне-өзі түйіндес оператор

Білімгер __ Ахметбекова Ұлмекен Тобы М18-1(к)

/Аты-жөні. / /қолы/

Жетекші Мусилимов Б.

/Аты-жөні. / /қолы/

Қорауға жіберілді «__20___» Мамыр 2021_г.

Қорғалды «__27___» Мамыр 2021_г. , бағасы

Комиссия мүшелері: Мусилимов Б. . _

/Аты -жөні/ /қолы/

Сулеймбекова А. О. _

/Аты-жөні/ /қолы/

Тараз - 2021ж.

ТАПСЫРМА

Функционалды анализ пәні бойынша

курстық жобаға, жұмысқа білімгер Ахметбекова Ұлмекен

1. ТақырыбыГильберттік кеңістіктегі өзіне өзі түйіндес оператор
2. Тапсырма бойынша арнайы нұсқаулар

Тапсырма “” Наурыз 20_ _ ж. № хаттамамен кафедра мәжілісінде бекітілді.

ЖетекшіМуслимов Б.

(аты-жөні, қызметі) (қолы)

Тапсырма орындауға қабылданды «_»__Наурыз__2021_ ж.

(білімгердің қолы)

МАЗМҰНЫ:

КІРІСПЕ . . . 3

НЕГІЗГІ БӨЛІМ . . . 6

ТҮЙІНДЕС КЕҢІСТІК

1. Функционал және сызықты функционалдар. Мысалдар . . . 6
2. Түйіндес кеңістікке мысалдар . . . 7

ГИЛЬБЕРТТІК КЕҢІСТІКТЕГІ ӨЗІНЕ ӨЗІ ТҮЙІНДЕС ОПЕРАТОР

1. Түйіндес оператор . . . 10
2. Өзіне өзі түйіндес оператор . . . 10
3. Өзіне өзі түйіндес оператор Гильберт кеңістігінде . . . 11

ҚОРЫТЫНДЫ . . . 13

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 16

Кіріспе

Бұл курстық жұмыс түйіндес операторлардың оның ішінде Гильберттік кеңістіктегі түйіндес операторларды зерттеуге бағытталған.

Осы курстық жұмыстың мақсаты - математикаға қызығушылық танытқандарды операторлардың спектрлік теориясымен, атап айтқанда, түйіндес операторларға арналған теоремалар, тұжырымдар және де леммалармен таныстыру. Олардың маңызды тұстарын атап көрсету.

Зерттеу жұмысының міндеті: түйіндес операторлар оның ішіндегі Гильберттік кеңістіктегі өзіне өзі түйіндес операторларды функционалды анализдегі алатын орны туралы баяндау .

• дамудың тиімді жолдарын іздеу мен анықтауда теоремалар мен леммалардың қолданып, оның дәлелдеуін көрсету.
• Дамыту перспективасын талдау және анықтау мақсатында тақырыптың мазмұнын аша түсу үшін әр түрлі жағдайларда орын алатын есептерге талдау жасау.

Тақырыптың өзектілігі: Операторларда Гильберттік кеңістіктегі өзіне өзі түйіндес операторларды зерттеу тиімді болып табылады. Себебі, Гильберттік кеңістікте операторлардың маңызды классын анықтауға болады. Яғни, Гильберт кеңістігі H -та анықталатын сызықтық операторларды қарастырсақ, онда мұндай жағдайда H пен $H^{*}$ бірдей болғаны және ондағы элементтердің скаляр көбейтінді болатынын пайдалана отырып, ерекше қасиетті симметриясы бар немесе өзіне өзі түйіндестік қасиеті деп айтылытын операторлар класын ажыратуға болады және де осы класстың операторларын зерттейтін боламыз.

Ал енді, курстық жұмыс құрылымына келер болсақ, ол кіріспеден, негізгі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен құралады.

Үш тараудан тұрады;

1. Түйіндес кеңістік
2. Гильберт кеңістігіндегі өзіне өзі түйіндес операторлар

Бірінші тарауда түйіндес кеңістік тарауының мазмұнын ашу үшін ең алдымен функционалдар және сызықты функционалдарға тоқталып өттім. Мұндағы негізгі деген ұғымдарға және теоремаларға түсінік жасадым. Негізгі анықтамаларына, қасиеттеріне шолу жасадым. Әр түрлі есептерге мысалдар көрсеттім. Сондай - ақ бұл тарауда түйіндес оператор анықтамасына, тоқталдым және де түйіндес операторға арналған мысалдарды қарастырдым.

Екінші тарауда бірнеше теоремалар мен тұжырымдарға тоқталып, дәлелдеуін көрсеттім. Сондай-ақ Гильберттік кеңістіктегі өзіне өзі түйіндес операторлар туралы теореманы талдап, дәлелдеуін көрсеттім. Осыған байланысты бірнеше есептерге талдау жасадым. Сонымен қатар, сызықты $A$ операторының характеристикалық саны, регулярлық саны, спектры, меншікті мәні, меншікті векторы деген терминдерге де жалпылама түсінік беріп өттім.

1. ТҮЙІНДЕС КЕҢІСТІКФункционал және сызықты функционалдар. Мысалдар.

$L$ кез- келген сызықтық кеңістік берілсін. Осы кеңістікте элементтерінде анықталатын сан мәнді $f(x)$ функциасын функционал деп атаймыз.

Бұл жерде, $f$ сәйкестікті анықтайды, ал $f(x)$ $x$ элементіне қойылатын санды белгілейді. $L$ кеңістігінің құрылымы $f(x)$ нақты немесе комплекс мәнді функционал болуы керек. Мысалы, $\ \ f(x) = \ x\$ кез келген жағдайда нақты мәнді функционал болады.

Егер, $f(x)$ функционалына байланысты мынандай екі нақты шарт орындалса:

1. Кез-келген, x, y∈Lx, y \in Lүшінf(x+y) =f(x) f(x + y) = f(x) +f(y) \ f(y) (адитивтік шарты)
2. Кез-келгенλ\lambdaсаны үшінf(λx) f(\lambda x) =f(x) =λf(x) \ f(x) = \lambda f(x) (біртектілік шарты)

онда $f(x)$ сызықты функционал деп атаймыз. Бұл екі шартты біріктірсек, мынандай бір теңдікті аламыз.

$f(\alpha x + \beta y) = \alpha f(x) + \beta f(x)$

мұндағы α және β кез-келген сандар. Бұл теңдік анықтама бойынша екі шартқа негіз болғандықтан, функционалдың сызықты екенін тексеру үшін $f(\alpha x + \beta y) = \alpha f(x) + \beta f(x)$ теңдігін тексерсе жеткілікті болады.

Сызықтық функционалға мысалдар қарастыра кетейік.

1. L=RnL = R^{n}кеңістігініңx=(ε1, …, εn) x = (\varepsilon_{1}, \ldots, \ \varepsilon_{n}) элементіндеf(x) f(x)

функционалының мәні

$$f(x) = (\alpha\varepsilon_{1} + \ldots + \ {\alpha_{n}\varepsilon}_{n})$$

теңдігімен анықталады, мұндағы $\alpha_{1}, \ldots, \ \alpha_{n}$ тұрақты сандар. Бұл жерден функционалдың адитивтік және біртектілік қасиеттерін анықтау оңайырақ. $R^{n}$ кеңістігінде анықталатын бұл функционал кәдімгі $n$ айнымалы сызықтық функция екеніне назар аударсақ, $R^{n}$ кеңістігіндегі сызықтық функционал тек осы түрде ғана бола алатындығы анықталады.

2. L=C[a, b] L = C\lbrack a, b\rbrackсызықты кеңістігініңf(x) f(x) функционалыныңx(t) x(t) элементінде функционал мәні

$$f(x) = \int_{a}^{b}{x(t) dt}$$

теңдігімен анықталады. Бұл функционалдың сызықты қасиеті интегралдың аддитивтік және біртектілік қасиеттері арқылы шығады.

3. L=L[a, b] L = L\lbrack a, b\rbrackқосынды болатын функциялар кеңістігіндеf(x) f(x) функционалx(t) x(t) элементінің мәні кез келген шенелген, тиянақтыa(t) a(t) функциясы үшін

$$f(x) = \int_{a}^{b}{a(t) x(t) dt}$$

теңдігімен анықталады. Бұл функционалдың сызықты қасиетін интегралдың аддитивтік және біртектілік қасиеттерінен шығатынын байқаймыз және бұл $$ $$f(x) = \int_{a}^{b}{x(t) dt}$$

функцияның жалпы түрі болады.

4. L=C[a, b] L = C\lbrack a, b\rbrackкеңістігінде анықталған тағы да бір функционал

$$\delta_{t_{0}}(x) = x\left( t_{0} \right)$$

$\delta_{t_{0}}$ функционал $x(t) \in C\lbrack a, b\rbrack$ элементінің мәні $x\left( t_{0} \right)$ санына тең. Анықтаушы теңдік $\delta_{t_{0}}(x) = x\left( t_{0} \right)$ бойынша

$$\delta_{t_{0}}(\alpha x + \beta y) = \alpha x\left( t_{0} \right) + \beta x\left( t_{0} \right) = \alpha\delta_{t_{0}}(x) + \alpha\beta(y)$$

Демек бұл сызықты функционал болады.

5. L=l1L = l_{1}сызықты кеңістігі үшінx=(ε1, …, εk) ∈l1x = (\varepsilon_{1}, \ldots, \ \varepsilon_{k}) \in l_{1}кез- келген

$a = (\alpha_{1}, \ldots, \ \alpha_{k}) \ldots \in m$ тиянақты элемент берілсін. Функционалды

$$f(x) = \sum_{k = 1}^{\infty}{\alpha_{k}\varepsilon_{k}}$$

Екенін көреміз. Бұл кеңістіктегі элементтерді қосу және көбейту амалдары координаторға қолданылатын болса, егер α мен β кез-келген сандар, онда $y = (\eta_{1}, \ldots, \ \eta_{k\ldots}) \in l_{1}$ болатын болса онда

$$f(x) = (\alpha x + \beta y) = \sum_{k = 1}^{\infty}{\alpha_{k}{(\alpha\varepsilon}_{k} + {\beta\eta}_{k}) } = \alpha\sum_{k = 1}^{\infty}{\alpha_{k}\varepsilon_{k} + \beta\sum_{k = 1}^{\infty}{\alpha_{k}\eta_{k} = \alpha f(x) + \beta f(y) }}$$

яғни, бұл сызықты функционал болады.

1. Түйіндес кеңістіктер. Мысалдар

Анықтама: N нормаланған сызықты кеңістік сызықты функционал $\ \Lambda\left( N, R^{1} \right)$ сызықты кеңістік N кеңістігіне түйіндес кеңістік деп аталады.

N кеңістігіне түйіндес болатын кеңістікті N* деп аталады. Анықтамаға сәйкес бұл кеңістік барлық $f \in N^{*}$ элементі сызықты функционал болса оның нормасы жоғарыда

$$\left\ \mathbf{f} \right\\mathbf{=}\sup\frac{⃒f(x) ⃒}{\left\ x \right\}$$

Теңдігі арқылы анықталады және ол норманың аксиомаларындағы шарттар бойыншы анықталады. Сол себепті $N^{*}$ - сызықты нормаланған кеңістік.

Мысалы $R^{n}\ кеңістігіне\ түйіндес\$ $R^{n*}$ кеңістігін анықтайтын болсақ алдын ала, $R^{n}$ кеңістігінде анықталатын кез-келген сызықты функционал

$$f(x) = (\alpha\varepsilon_{1} + \ldots + \ {\alpha_{n}\varepsilon}_{n})$$

түрінде болатынын дәлелдейміз.

Сонда, $f(x)$ осы кеңістікте кез-келген сызықты функционал, ал $е_{1}, \ldots, е_{n}$ векторлары осы кеңістіктегі базис болсын. Онда кез-келген ${x \in R}^{n}$ векторы $f(x) = \left( \varepsilon_{1}e_{1} + \ldots + \ \varepsilon_{n}e_{n} \right) \$ түрінде жіктеледі. Бұл теңдікке сызықты функционалды қолдансақ $f(x) = \left( \varepsilon_{1}{f(e}_{1}) + \ldots + \ \varepsilon_{n}f(e_{n} \right) ) \$ теңдігі шығады. Енді функционалдың базис векторларының мәндерін $f\left( e_{i} \right) = a_{i}$ деп белгілесек $f(x) = (\alpha\varepsilon_{1} + \ldots + \ {\alpha_{n}\varepsilon}_{n})$ түріне келеді. Кеңістіктің барлық векторы базис бойынша бірмәнді болады. Сол себепті $f(x) = (\alpha\varepsilon_{1} + \ldots + \ {\alpha_{n}\varepsilon}_{n})$ $R^{n}$ кеңістігі функционалдың жалпы түрі болады.

$\ \ \ \ \ f(x) = (\alpha\varepsilon_{1} + \ldots + \ {\alpha_{n}\varepsilon}_{n})$ теңдігінде оң жағындағы n айнымалы сызықты функция, ол коэффиценттері, $a_{1}, \ldots, \ a_{n}$ сандары, берілетін болса, толық анықталуы керек. Бұл сандарды n өлшемді, $a = (a_{1}, \ldots, \ a_{n})$ векторы координаттары ретінде қарастырамыз. Демек, $f$ функционалы $a$ векторының берілуімен толық анықталады. Сол себепті, $f$ функционалы мен оны анықтайтын $a$ векторы бірігіп, тұтастай түрінде қабылдаймыз. Яғни, $f$ функционалы деп отырғанымыз $a$ векторы. Ал, ${\alpha \in R}^{n}$ сол себепті $R^{n}$ кеңістігін құрайды, демек, ${R^{n*} = R}^{n}$ . Бірінші қарастырған мысалда түйіндес кеңістік бастапқы кеңістіктің өзі болды, яғни $R^{n}$ - өзіне өзі түйіндес кеңістік. Бірақ кейін бұл тек кейбір кеңістіктерге ғана тән болатынын көреміз.

Ескерту. $R^{n}$ кеңістігі сызықты функционалдың жалпы түрін анықтайтын $f(x) = (\alpha\varepsilon_{1} + \ldots + \ {\alpha_{n}\varepsilon}_{n})$ теңдігіне тұрақты $a$ векторы мен айнымалы $x$ векторының скаляр көбейтіндісі түрінде, яғни $f(x) = (a, x)$ түрінде де қарастыруға болатынын қарастырайық.

Қарастырылған мысалдар арқылы нормаланған сызықтық $N$ кеңістігіне түйіндес ${\ \ \ \ \ \ N}^{*}$ кеңістігін анықтау үшін $N$ кеңістігіндегі сызықты функционалдың жалпы түрін білу керек екені айқын.

Енді, түйіндес кеңістіктің жалпылама қасиеті жайлы мына бір тұжырымды дәлелдей кетейік.

Теорема. Түйіндес кеңістік $\mathbf{N}^{\mathbf{*}}$ әрқашан толық кеістік.

Дәлелденуі. $\left\{ f_{n} \right\}$ , $\left\{ f_{n} \right\} \in N^{*}$ тізбегі фундаменталь тізбек болса онда кез келген $\ \varepsilon > 0$ берілгенінде барлық $n$ , $m > n_{0}(\varepsilon)$ номерлері үшін

$$\left\ f_{n} - f_{m} \right\ < \varepsilon$$

теңсіздігі орындалса $n_{0}(\varepsilon)$ саны табылатындай болсын. Норманың анықтамасын ескере отырып, $\left\ f_{n} - f_{m} \right\ < \varepsilon$ теңсіздігінің салдары ретінде

$⃒f_{n}(x) - f_{m}(x) / < \varepsilon\left\ x \right\$ ,

теңсіздігі $N$ кеңістігіндегі кез келген $x \in N$ үшін болады және $\left\ x \right\$ тұрақты, ал $\varepsilon > 0$ кез-келген сан болғаны үшін, $f_{n}(x) - f_{m}(x) / < \varepsilon\left\ x \right\$ теңсіздігі $\left\{ f_{n}(x) \right\}$ тізбегі үшін Коши критерийі орындалатыны айдан анық. Яғни, бұл тізбектің шегі бар, оны $f(x)$ арқылы таңбалаймыз. Сызықты функционалдардың шегі $f(x)$ функционалы да сызықтық қасиетін сақтайды. Шынында да, $f_{n}(\alpha x + \beta y) = \alpha f_{n}(x) + \beta f_{n}(x)$ себебі $f_{n}$ - сызықты функционал болады. Осы теңдікте шекке көшсек, $f(\alpha x + \beta y) = \alpha f(x) + \beta f(x)$ теңдігін шығады, яғни $f$ - сызықты функционал. Сандар тізбегінің $⃒f_{n}(x) f_{m}(x) / < \varepsilon\left\ x \right\$ теңсіздігінде $m \rightarrow \infty$ кезде шекке көшсек,

$⃒f_{n}(x) - f(x) ⃒ \leq \varepsilon\left\ x \right\$

теңсіздігіне келеміз. Осы теңсіздіктен

$$\left\ f_{n} - f \leq \varepsilon \right\$$

Демек $f_{n}$ - $\ f$ шенелген функционал екендігі белгілі. Ал,

$$\left\ f \right\ = \left\ f - f_{n} + f_{n} \right\ \leq \left\ f - f_{n} \right\ + \left\ f_{n} \right\\mathbf{\leq}\left\ f_{n} \right\\mathbf{+}\varepsilon$$

енді, $f_{n}$ шенелген функционал болғаны үшін, бұл теңсіздіктен $f$ - функционалының шенелгендігін байқаймыз, яғни ол үздіксіз функционал. Қорыта келе, $N^{*}$ кеңістігіндегі шенелген функционалдың $\left\{ f_{n} \right\}$ фундаменталь тізбегінің шегі $f$ бар және ол шенелген сызықты функционал болатыны, яғни $f \in N^{*}$ екені дәлелденді. Яғни, $N^{*}$ толық кеңістік. Теорема дәлелденді.

Мысалы: 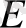- - 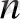өлшемді сызықты кеңістік берілсін, және де базисін таңдап аламыз. Сонда барлық векторлар 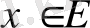үшін 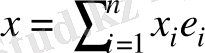түріне келеді. Егер 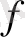сызықты функционал болса, онда

.

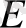
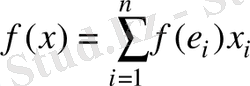болатыны анық.

Сәйкесінше сызықты функционалдың мәні векторлы базисінде анықтады.

2. ГИЛЬБЕРТТІК КЕҢІСТІКТЕГІ ӨЗІНЕ ӨЗІ ТҮЙІНДЕС ОПЕРАТОРТүйіндес оператор

$Y$ түйіндес кеңістігіне $A \in L(X, Y), Y^{*}$ - берілсін. $\left\langle Ax, f \right\rangle$ функционалының мағынасын $F \in Y^{*}$ элементінде $y = Ax \in Y$ қарастырайық.

$g(x) = \left\langle x, g \right\rangle = \left\langle Ax, f \right\rangle$ деп белгілеп алып

1. g:Dg=Xg:D_{g} = Xанықталу облысы
2. ggсызықты шенелген

болсын. Яғни $g \in X^{*} = L(X, R)$ . Осылайша біз түйіндес оператор деп аталатын бейнелеу құрастырамыз

$A^{*}:Y^{*} \rightarrow X^{*}: ⩝ f \in Y^{*} \rightarrow g \in Y^{*}$ .

$R$ -ден алынатын кез келген $x, y$ үшін $(Ax, y) = \left( xA^{*}y \right)$ теңдігі дұрыс болатынын сызықты $A^{*}\$ операторы $A$ түйіндесі деп айтаймыз. $R$ евклид кеңістігінде $\overline{x, }\overline{y}$ векторлары үшін $(Ax, y) = \left( xA^{*}y \right)$ орындалса $A$ $A^{*}\$ -ға түйіндес деп аталады.

Лемма: Егер $R$ евклид кеңістігінде барлығы $\overline{x}$ векторлары үшін $(x, U) = (x, V)$ орындалатын болса, онда $U = V$ орындалатыны анық. .

Дәлелдеуі:

$(x, U) = (x, V)$ теңдігінен $\overline{x}\$ кез- келген үшін $(x, U - V) = 0$ болады. $X = (U - V)$ теңдігін негіздей келе, $\ (U - V, U - V) = 0$ теңдігін аламыз. Бірақ $R$ евклид кеңістігі болғаны үшін $U - V = 0$ және $U = V$ болары анық.

$R$ евклид кеңістігі және $A$ ондағы сызықты оператор болсын. Ал, $y$ үшін $f_{y}(x) = (Ax, y)$ көбейтіндісі $x$ -ке қатысты бар сызықты функционал болады. Демек,

... жалғасы

Сызықтық кеңістікке түйіндес кеңістік

Түйіндес операторлар

Жай дифференциалдық теңдеулер және операторлар

Гиперболалық операторлардың бір класының өз-өзіне түйіндестігін көрсету

n-өлшемді векторлық кеңістк

Оператор, унитар оператор

Гиперболалық түрдегі оператордың бір класының симметриялы болатындығы туралы мәселені зерттеу

Физикалық шамалардың операторлары

Жойылмалы эллиптік түрдегі оператордың бір класының оң анықталғандығы туралы

Сызықты кеңістіктер

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс