Матрицалар мен анықтауыштар: негізгі ұғымдар, қасиеттері және есептеу әдістері


Жоспар:
Кіріспе.
Матрица және анықтауыштар . . . 2
1. Негізгі ұғымдар . . . 2
1. 1 Матрицаларға амалдар қолдану . . . 3
2. Анықтауыштар . . . 4
2. 1Анықтауыштың қасиеттері . . . 5
3. Ерекше емес матрицалар . . . 7
3. 1 Кері матрица . . . 7
3. 2 Матрицаның рангсі . . . 8
4. Қорытынды . . . 25
Қолданылған әдебиеттер . . . 26
Кіріспе.
Матрицалық әдіс пен Крамер ережесінің негізгі екі кемшілігі бар.
Біріншіден, оларды нұқсансыз матрицалары бар теңдеулер жүйесіне ғана қолдауға болады.
Екіншіден, сандық теңдеулер жүйесін шешуде тиімсіз, өйткені ол әдістерді қолдану(Гаусс әдісіне қарағанда) n2 есеге жуық есептеу амалдарын жасауды керек етеді, мысалы, n>10 болса, онда бұл әдістерді қолдану мүмкіндігі тіпіті аз.
Элементар түрлендіру Гаусс әдісі кез келген тік бұрышты (квадрат қана емес) матрицалары бар теңдеулер жүйесін зерттеп және шешімін табуға (жүйенің шексіз көп шешімі бар жағдайда да ) мүмкіндік береді.
Теңдеулер жүйесін зерттеу-оның үйлесімді немесе үйлесімсіз екенін, ал егер үйлесімді болса, онда жүйе шешімнің қанша болатынын анықтау.
Анықтама. САТЖ-нің кеңейтілген матрица деп жүйе матрицасының оң ағынан бос мүшелер бағанын тіркеп жазу арқылы алынған матрицаны айтады( тіркелген бос мүшелерді әдетте вертикаль сызықпен бөліп қояды) . Мысалы, 1-САТЖ матрицасы өлшемді болса, онда оның кеңейтілген матрицасы өлшемді болады:
Оладың рангтерінің екі жағдайы: немесе болуы мүмкін. Келесі теорема теңдеулер жүйесін зерттеуге мүмкіндік береді.
Теорема(Кронекер-Капелли) . Сызықтық алгебралық теңдеулер жүйесінің матрицасы мен кеңейтілген матрицасының рангілдері тең болса, жүйе үйлесімді болады. Енді теңдеулер жүйесін Гаусс схемасы бойынша зерттеу және шешу сұрақтарын қарастырайық.
Гаусс әдісімен және матрицаларының рангілерін анықтау үшін-кеңейтілген матрицасын жазып алып элементар түрлендірулер арқылы матрицасы трапеция тәріздес матрицаға келтіріледі. Егер бұл түрленділулерде бағандар орын алмасқан болса, оларды өздеріне сәйкес белгісіздермен белгілеп отырады.
Трапеция тәріздес матрица рангісі туралы жоғарыда қарастырғанбыз.
Матрица және анықтауыштар
1. Негізгі ұғымдар
m -жатық жолдан және n -тік жолдан тұратын сандардан құралған тікбұрышты кесте матрица деп аталады. Матрица
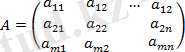
түрінде жазылады немесе қысқаша түрде А =( а ij ), мұндағы i=1, m (яғни i=1, 2, 3, …, m ) - жатық жол нөмірі, j=1, n (яғни j=1, 2, 3, …, n ) - тік жол нөмірі. Ал А матрицасын m×n өлшемді матрица деп атайды және A m×n деп жазады. Матрицалар құралған а ij саны матрицаның элементтері деп аталады. Жоғары бұрышынан шығатын диагональда орналасқан элементтері бас диагональды құрайды.
Егер екі матрицаның барлық сәйкес келетін элементтері тең болса, онда мұндай матрицалар өзара тең болады, яғни
Егер матрицаның жатық жолдар саны тік жолдар санына тең болса, ондай мұндай матрицаны - квадрат матрица деп атайды. n×n өлшемді квадрат матрицаны n өлшемді квадрат матрица деп атайды. Бас диагоналінің элементтерінен басқа элементтерінің бәрі нөлге тең квадрат матрица диагональдық матрица деп аталады. Бас диагональдің элементтерінің барлығы бірдей бірге тең диагональдық матрица бірлік матрица деп аталады. Бірлік матрица Е әрпімен белгіленеді.
Егер квадрат матрицаның бас диагоналінің бір жағында орналасқан элементтерінің барлығы нөлдер болса, онда мұндай матрица үшбұрышты матрица деп аталады.
Барлық элементтері нөльге тең матрица нөлдік матрица деп аталады. Нөлдік матрица О әрпімен белгіленеді.

(1. 3)
белгіленеді.
Матрицалық есептеулерде О және Е матрицалары арифметикада 0 және 1 сандары рөлін атқарады. Бір жатық жолдан немесе бір тік жолдан тұратын матрица векторлық деп аталады (немесе тік жол матрица немесе жатық жол) жалпы түрі:
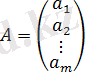 .
.
(1. 4)
Бір санынан тұратын 1 × 1 өлшемді матрица сол санға теңестіріледі, яғни (5) 1 × 1 5-ке тең.
Егер матрицаның барлық жатық жолдарын сәйкес сол нөмерлерімен тік жол етіп ауыстырғаннан шыққан матрица транспозицияланған матрица деп атайды.
1. 1 Матрицаларға амалдар қолдану
Қосу
Матрицаларды қосу амалдары бірдей өлшемді матрицалар үшін орындалады. A m × n =( а ij ) және B m × n =( b ij ) матрицаларының қосындысы деп элементтері c ij = a ij + b ij ( i =1, m ; j =1, n ) болатын C m × n =( c ij ) матрицасын айтады.
Матрицалар айырымы тура осылайша анықталады.
Матрицаны санға көбейту
A m × n =( а ij ) матрицасын к санына көбейтіндісі деп элементтері b ij =k* а ij , ( i =1, m ; j =1, n ) болатын B m × n =( b ij ) матрицасын айтады.
Матрицалардың қарапайым түрленуі
- матрицаның екі параллель қатарының орындарын ауыстыру;
- матрицаның қатарының барлық элементтерін нөлге тең емес санға;
- матрицаның қатарының барлық элементтерін нөлге тең емес санға көбейту;
- матрица қатарының барлық элементтеріне параллель қатардың сәйкес элементтерін бір санға көбейтіп қосу;
- А және В матрицалары эквивалент матрицалар деп аталады, егер оның біреуі екіншісін элементар түрлендіру арқылы алынса.
Кез-келген матрицаны элементар түрлендірулер арқылы бас диагональдарында бірлер, қалған элементтері нөлге тең матрицасына келтіруге болады. Мұндай матрицаны канондық (қарапайым) матрица деп атайды, мысалы:
 .
.
Матрицаларды көбейту
Матрицаларды көбейту амалы бірінші матрицаның тік жолдар саны екінші матрицаның жатық жолдар санына тең болғанда ғана орындалады.
A m × n =( а ij ) матрицасының B m × n =( b ij ) матрицасына көбейтіндісі деп элементтері c ik = а i1 ∙ b 1k + а i2 ∙ b 2k +…+ а in ∙ b nk , мұнда i =1, m ; k=1, p арқылы анықталатын C m × p =( c ik ) матрицасын айтады, яғни С матрицасының і -ші жатық жол және к -ші тік жол элементі А матрицасының і -ші жатық жолы В матрицасының к -ші тік жол сәйкес элементтерінің көбейтінділерінің қосындысы. c ik элементін келесі схема бойынша көрсетуге болады:
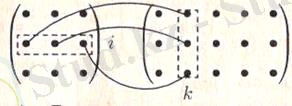
Егер А және В өлшемдері бірдей квадрат матрицалар болса, онда АВ және ВА көбейтінділерін табуға болады. АЕ=ЕА=А екендігін оңай көрсетуге болады, мұнда А - квадрат матрица, Е - бірлік матрица.
2. Анықтауыштар
n
ретті А квадрат матрицасына
det
A саны (немесе
 ) сәйкес анықтауышын анықтауға болады:
) сәйкес анықтауышын анықтауға болады:
А матрицасының анықтауышын детерминант деп те атауға болады. N ретті А матрицасының детерминантын есептеу ережесі қолдану және қабылдау өте күрделі. Жоғары ретті анықтауышты есептеу әдістері төменгі ретті анықтауыштарды есептеу негізінде жүзеге асырылады. Анықтауыштарды есептеудің әдістерінің бірі, ол анықтауышты қандай да бір қатар арқылы жіктеу қасиеттеріне негізделген (7-қасиет) . 1-ші, 2-ші, 3-ші ретті анықтауыштарды анықтамалары бойынша есептеуге болады.
1 . n =1.
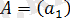 ; detA=
; detA=
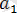 .
.
2. n =2.
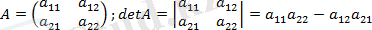 .
.
3. n =3

 .
.
2-ші ретті анықтауышты есептеу схемасы:
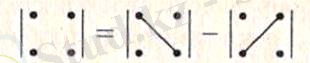
3-ретті анықтауышты есептеу үшін үшбұрыштар әдісін (немесе Саррюс) қолданған ыңғайлы. Символдық түрде

2. 1 Анықтауыштың қасиеттері
Анықтауыштың барлық реттеріне қатысты анықтауыштың негізгі қасиеттері келтіріледі. Осы қасиеттердің кейбір қасиеттері 3-ретті анықтауыштарымен келтіріледі.
1-қасиет. Анықтауыштың жатық жолдары мен сәйкес тік жолдарының орындарын ауыстырса, одан анықтауыштың мәні өзгермейді, және керісінше де осылай болады. Жатық жолдар мен тік жолдарды анықтауыштың қатары деп те атауға болады.
2-қасиет. Анықтауыштың параллель орналасқан екі қатарының (кез-келген екі жатық жол немесе екі тік жол) орындарын ауыстырса, одан анықтауыштың таңбасы қарама-қарсы таңбаға өзгереді.
3-қасиет. Егер анықтауыштың екі қатары бірдей болса, онда анықтауыштың мәні нөлге тең болады.
4-қасиет. Анықтауыштың кез-келген бір қатарында ортақ көбейткіші болса, онда оны анықтауыш таңбасының алдына шығаруға болады. Анықтауыштың 3-ші және 4-ші қасиеттерінен, анықтауыштың кез-келген бір қатарының элементтері сәйкес қатарының элементтеріне пропорционал болса, онда анықтауыштың мәні нөлге тең болатыны шығады.
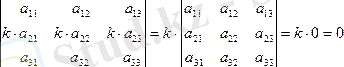 .
.
(1. 8)
5-қасиет. Егер анықтауыштың кез-келген қатарының элементтері екі санның қосындысынан тұрса, онда анықтауыш сәйкес екі анықтауыштың қосындысы түрінде жіктеледі.
6-қасиет. («Анықтауыштың қарапайым түрленуі») Егер анықтауыштың кез-келген бір қатарының элементтерін нөлге тең емес бір санға көбейтіп, параллель жатқан екінші бір қатардың элементтеріне апарып қосса, одан анықтауыштың мәні өзгермейді.
Анықтауыштың a ij элементінің миноры деп анықтауыштың жатық жолы мен тік жолын сызып тастағанда қалған ( n-1 ) -ретті анықтауышты айтады. Сызып тастағанда қиылысындағы элемент a ij -ға сәйкес минорды M ij деп белгілейді.
Анықтауыштың a ij элементінің алгебралық толықтауышы деп егер i+j -жұп сан болса «плюс» таңбасы, ал егер i+j -тақ сан болса «минус» таңбасы мен алынған a ij элементінің минорын айтады. A ij алгебралық толықтауышы келесі түрде белгіленеді:
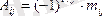 ,
,
яғни A 11 =+m 11 , A 32 =-m 32 .
7-қасиет. («Анықтауышты кез-келген қатары бойыншы жіктеу») . Егер анықтауыштың кез-келген қатары элементтерін өздеріне сәйкес алгабралық толықтауыштарына көбейтіп, шыққан көбейтінділерін қосса, ол қосынды анықтауыштың мәніне тең болады.
3. Ерекше емес матрицалар
А матрицасы n -ретті
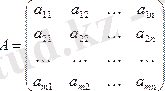
(1. 10)
квадраттық матрицаның анықтауышы Δ=det≠0 нөльге тең болмаса, онда матрица ерекше емес матрица деп аталады. Қарама қарсы жағдайда Δ=0 болса, А матрицасы ерекше деп аталады.

(1. 11)
матрицасы А матрицасына одақтас матрица деп аталады, мұнда A ij - a ij элементінің алгебралық толықтауышы деп аталады (ол анықтауыштың элементінің алгебралық толықтауышы сияқты анықталады) .
Егер
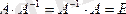 ,
,
(1. 12)
теңдігі орындалса, онда A -1 матрицасы А матрицасына кері матрица деп аталады, мұндағы Е -бірлік матрица, өлшемі А матрицасының өлшемімен тең A -1 матрицасының да өлшемі А матрицасымен бірдей.
3. 1 Кері матрица
Теорема. Ерекше емес матрицаның кері матрицасы болады.
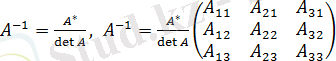 .
.
(1. 13)
Кері матрицаның қасиеттері:
1.
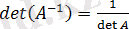 ;
;
2.
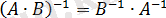 ;
;
3.
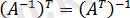 .
.
3. 2 Матрицаның рангісі
m×n өлшемді А матрицасын қарастырайық.
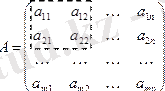
(1. 14)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz