Дискреттік сигналдарды Фурье түрлендіру

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 37 бет
Таңдаулыға:

Қазақстан Республикасының Білім және ғылым министрлігі
Л. Н. Гумилев атындағы Еуразия ұлттық университеті

Балмаш Д. Б.

ГЕОРАДИОЛОКАЦИЯЛЫҚ СИГНАЛДАРДЫ КӨРНЕКІЛЕУ

ДИПЛОМДЫҚ ЖҰМЫС

мамандық 5B070400 - Есептеу техникасы және бағдарламалық қамтамасыз ету

Нұр-Сұлтан 2020Қазақстан Республикасының Білім және ғылым министрлігі

Л. Н. Гумилев атындағы Еуразия ұлттық университеті

Қорғауға жіберген
Есептеу техникасы
кафедрасының меңгерушісі
т.ғ.к., PhD
Дюсекеев К. А.___________
_____________________2020

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: Георадиолокациялық сигналдарды көрнекілеу

5B070400 - Есептеу техникасы және бағдарламалық қамтамасыз ету мамандығы

Орындаған Балмаш Д. Б., ЕТБҚ-45 тобының студенті

Ғылыми жетекшісі Боранбаев С. А.

Нұр-Сұлтан 2020

МАЗМҰНЫ
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 4
Негізгі бөлім ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 5
1. Сигналдарды цифрлық өңдеудің негіздері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...5
1.1. Дискреттік сигналдарды Фурье түрлендіру ... ... ... ... ... ... ... ... ... ... ... ...5
1.2. Цифрлық сигналдарды вейвлет түрлендіру ... ... ... ... ... ... . ... ... ... ... ... ..6
1.3. Цифрлық сигналдарды сүзу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .11
2. Георадиолокациялық сигналдарды талдау әдістері ... ... ... ... ... ... ... ... ... ... ...17
2.1. Георадиолокация негізде ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 17
2.2. Георадарлар және олардың жұмыс тәртібі ... ... ... ... ... ... ... ... ... ... ... ..17
2.3. Георадиолокациялық сигналдарды цирфлық өңдеу ... ... ... ... ... ... ... .. ..
2.4. Георадиолокациялық сигналдарды вейвлет талдау ... ... ... ... ... ... ... . ...

Кіріспе
Георадиолокациялық сигналдар жер қабатын зерттейтін күрделі жүйелік құрылғыдан - георадардан алынады. Қазіргі уақыттағы георадарлар құрылғылық, яғни таратушы және қабылдағыш антенналар, бағдарламалық қамтамасыз ету мен олардың өзара сихронизациясынан тұратын күрделі электрондық құрылғы болып саналады. Сәйкесінше, аталмыш құрылғылар кәсіби емес зерттеу жұмыстарын жүргізіп, анализ жасау мақсатында қолдану үшін экономикалық тұрғыдан аса бір тиімді деп айтуға келмейді. Себебі, біріншіден, радардың аппараттық бөлімі мен қолданушыға арналған дербес компьютерлік бағдарлама бөлек сатылады, екіншіден олардың нарықтық бағасы қымбаттау болып келеді. Сол себептен, дипломдық жұмыс ретінде георадиолокациялық сигналдармен жұмыс жасауға арналған жаңа бағдарламалық қамтамасыз етуді жасап шығару бағыты алынған болатын.
Дипломдық жұмыстың мақсаты - георадиолокациялық сигналдарды көрнекілеуге арналған бағдарламаны жасау. Бұл бағдарлама сигналдар жазылған файлды оқып, оны графикалық түрде көрнекілеп көрсету.
Дипломдық жұмыс жоғарыда атап өткен сигналдарды графикалық түрде екі режимде: жалпы және түрлі - түсті режимде сипаттау, құрылған графикті сақтау функциясын жасау тапсырмаларын іске асырады.

1. Сигналдарды сандық өңдеу негіздері

1.1. Дискреттік сигналдарды Фурье түрлендіру
Сигналдарды сандық өндеу(ССӨ) әдістері қазіргі уақытта аналогты өңдеуге негізделген әдістерді біртіндеп ығыстыра отырып, кеңінен қолданысқа ие болып жатыр. ССӨ міндеттерінің кең спектрінің болуы сигналдарды сандық өідеу үшін бейімделген архитектураға ие, басқарудың тиімді жүйесін құруға мүмкіндік беретін DSP (digital signal processing) сигналдық процессорларының пайда болуына әкелді. Басқарушы микропроцессорлар шешімді мерзімді түрде қабылдайды. Сондықтан микропроцессорлық басқару жүйелері сандық және импульстік жүйелерге жатады және автоматты басқарудың дискретті жүйелері атауымен біріктіріледі. Сигналдарды сандық өңдеу әдістері мен техникаларының қарқынды дамуы оның артықшылықтарының көп болуымен түсіндіріледі, олардың негізгілері:
* өңдеу дәлдігінің кепілділігі;
* нәтижелерді графикалық немесе басқа да түрде көрнекілеу;
* аналогты құрылғыларға тән температуралық және уақытша дрейф, параметрлердің шашырауы, кедергілер мен ауытқулардың әсері секілді тұрақсыздандыратын факторлардың болмауы;
* ақпаратты өңдеу алгоритмдерін бағдарламалық түрде іске асыру мүмкіндігі;
* басқару нысандарының параметрлерін өзгерту арқылы басқару жүйесін баптау мүмкіндігі;
* қайта іске асыралатын құрылымы бар бейімделу жүйелерін құру мүмкіндігі;
* аса бір еңбекті қажет ететін және прецизионды операцияларды пайдаланбай баптаудың оңайлығы.
Сигнал деп уақыт өтуіне байланысты белгілі бір ақпаратты немесе хабарды көрсететін физикалық процессті айтамыз.
Аналогтық сигнал (АС) амплитудасы мен уақыты бойынша кейбір мәндерді қабылдай алатын үздіксіз немесе x(t) бөлікті-үздіксіз функциясымен сипатталады.
Дискретті сигнал - бұл t=nT дискретті уақыт кездеріне алынған аналогтық сигналдың есептеулері(таңдаулар) тізбегі, мұндағы T = const - дискретизация интервалы, n - есептеу нөмірі, дискретті уақытты сипаттайтын бүтін сан(1-сурет, б). Бұл ретте n0 кезінде xnT=0. Дискретті сигналдар торлы x(nT) функциялармен сипатталады. x(nT) дискретті сигналдың мәндері есептеу деп аталады және t=nT, n=0, 1, 2,... уақыт кезінде x(t) бастапқы сигналының таңдауы болып табылады:

xnT=xa(t)t=nT. (1)

Сигналды таңдау T интервалымен, яғни fdдискреттеу жиілігі деп аталатын белгілі бір жиілікпен және ω дискреттеу шеңберлі жиілікпен алынады:
fd=1T; ωd=2PI ∙fd=2PIT. (2)
Сандық сигналдар деңгейі бойынша квантталған дискретті сигналдарды білдіреді және nT дискретті сәттерге квантталған h1,h2,...hn кванттау деңгейлерінің соңғы қатарынан мәнді қабылдайтын квантталған торлы xc(nT) функциялармен (квантталған тізбектермен) сипаттталады. Торлы x(nT) функциясы мен квантталған торлы xc(nT) функциясының арасындағы байланыс кванттаудың сызықты емес xcnT=Fк(x(nT)) функциясымен анықталады. Кванттау функциясын таңдаудың түрлі тәсілдері бар. Қарапайым жағдайда, егер кванттау ∆h= hl-hl-1=const тұрақты қадамымен реттелетін болса, кванттау функциясы келесі түрге ие болады:

xcnT=FкxnT=h1 егер xnT=h2+h12,hl егер hl+hl-12xnT=hl+1+hl2,hN егерhN+hN-12xnt. (3)

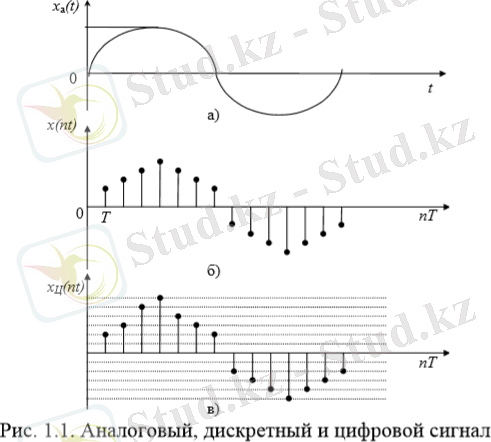
1-сурет. Аналогты, дискретті және сандық сигнал
Атап өткенімдей, сигнал деп физикалық тасымалдаушы, яғни беруге арналған ақпарат аталады. Сигнал ретінде әртүрлі физикалық параметрлері (қысым, температура, жарық және т.б.) болуы мүмкін. техникада көрсетілген параметрлердің уақыты мен кеңістігіндегі өзгерістер түрінде бастапқы ақпарат көзінен келіп түсетін сигнал теориялық зерттеу объектісі сигнал жасау үшін кернеу мен токтың өзгеру заңымен сипатталатын электр тербелісіне түрлендіріледі, сигналдың математикалық моделін енгізеді -- функционалдық тәуелділікті білдіретін оның математикалық сипаттамасының тәсілі, оның негізі уақыт -- s(t), x(t), u(t) болып табылады. Математикалық модель хабар тасымалдаушысының физикалық табиғатынан бөлінуге мүмкіндік береді және сигналдың аса маңызды қасиеттерін сипаттайды. Математикалық модельді енгізу сигналдарды аналогтық немесе құрлықтық жіктеуді шамасы бойынша еркін және уақыт бойынша үздіксіз сигнал деп атайды. Аналогтық x(t) сигналы үздіксіз немесе бөлікті-үздіксіз уақыт функциясымен сипатталады. Аргумент және функцияның өзі интервалдағы кез келген мәндерді қабылдайды:

xmin=x=xmax, (4)
tmin=t=tmax. (5)

Мысалға,

xt=exp-αt, 0=t=infinity (6)

Дискретті немесе импульсті сигнал уақыттың дискретті сәттерінде шамасы бойынша ерікті мәнді қабылдай алады. xд(t) дискретті сигналы торлы функциямен сипатталады - уақыттың тиісті сәттерінде іріктемелі мәндердің реттілігі:

x0=xt0, x1=xt1,...,xn=xtn. (7)

Дискретизацияның тұрақты интервалында

∆t=ti-ti-1=ti-1-ti-2=...=Tд (8)

Tд шамасын дискреттеу кезеңі деп атайды, ал оған кері шама - жиілікті дискреттеу деп атайды:
Fд=1Tд=1∆t. (9)
Бұл жағдайда торлы функцияның мәндері xnTд, x(n) немесе жәй ғана xn. Осылайша, дискретті сигнал төмендегідей сипатталады:
xдt=(x(nTд)) (10)
Аналогтық сигналдан дискретті сигналға өту -- дискретизация операциясы - берілген аналогтық сигналға дискретті сигналға сәйкес қойылады:
x(t)--xд(tn), (11)
Әрі қарай
xдnTд=x(nTд). (12)
Жоғарыда келтірілген мысал үшін
xдn=xдnTд=exp-αnTд=a-n, a=eαTд. (13)
Кері өту-қалпына келтіру операциясы - берілген дискретті сигналға сәйкесінше аналогты сигнал қойылады:
xд(tn)--x(t). (14)
Бұл операциялар есептеу теоремасының шарттарын орындау кезінде өзара кері болып табылады (Уиттекер -- Котельников -- Шеннон теоремалары). Сандық сигнал-бұл деңгей бойынша квантталған дискретті сигнал. Ол кванттау деңгейлері деп аталатын d0, d1, ...dk дискретті мәндердің соңғы қатарын қабылдайтын квантталған торлы функцияламен сипатталады. Торлы xn(nTд) функциясы мен квантталған торлы xc(nTд) функциясының арасындағы байланыс сызықтық емес функция - кванттаудың амплитудалық сипаттамасы Q(x)-пен анықталады:

Qx=d0+v=1K∆v1(x-av), (15)

мұндағы, ∆v=dv-dv-1 - кванттау қадамы, av - кванттау шегі, 1(x) - бір сатылы функция, K + 1 - кванттау деңгейлерінің саны.
Тұрақты қадам ∆v=∆ кванттау кезіндегі кванттаудың амплитудалық сипаттамасының жалпы түрі 2-суретте келтірілген.

2-сурет. Кванттаудың амплитудалық сипаттамасының жалпы түрі

Әрбір деңгей кодпен квантталады, және көбінесе екілік кодпен квантталады. Бұл жағдайда сандық сигналды сипаттайтын код разрядтарының саны төмендегідей анықталады:
m=int[log2(K+1)]. (16)
Мұнда int() функциясы берілген саннан кем емес, ең кіші бүтін санның анықтамасын білдіреді. Осылайша, дискретті сигналдан сандық сигналға көшу xд(nTд)--xc(nTд) кванттау және кодтау операцияларын қолдану арқылы жүзеге асырылады(3-сурет).

3-сурет. Аналогты(а), дискретті(б) және сандық(в) сигналдар

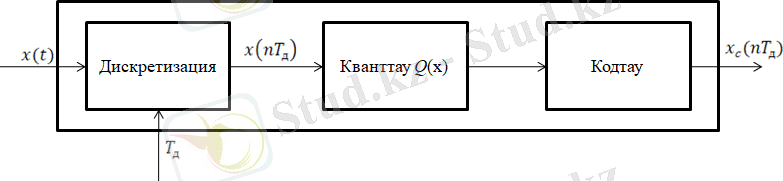
4-сурет. Аналогты-сандық түрлендірудің құрылымы
Бұл жағдайда сигналды бұрмалаудың екі түрі болуы мүмкін-дискретизация есебінен және кванттау деңгейлерінің соңғы саны есебінен.Сонымен қатар, сигналды беру дәлдігін арттыруға болады, бірақ бұл өңдеудің күрделенуіне және қымбаттауына әкеледі.
Кері өту процессі - сандық-аналогты түрлендіру берілген сандық сигнал бойынша x(t) сигналын құрудан тұрады:

xсnTд--xt, (17)

Бұл операциялар квантация кезінде қайтымсыз қателіктерге байланысты өзара кері болып табылмайды.
Дискретті сигналдарға мысалдар:
1. Дискретті дельта-функция (бірлік ипульс):

δnTд-kTд=0, n!=k;1, n=k. (18)

Бұл дискретті сигналдың көрінісі 5-суретте көрсетілген.

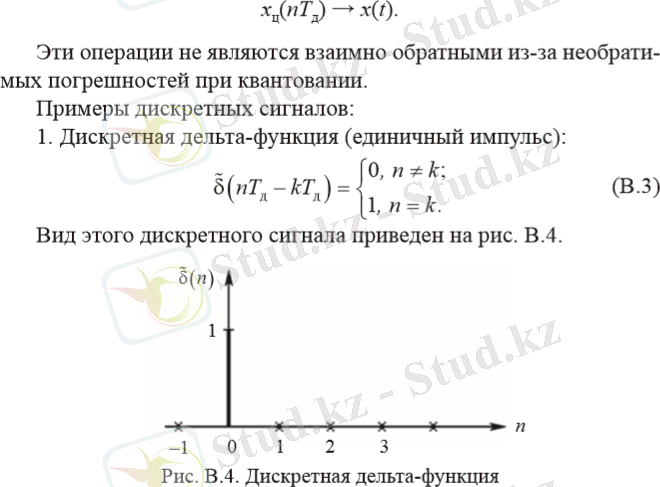
5-сурет. Дискретті дельта-функция
Дискретті сигналдар аналогтық сигналдар сияқты, сигналдардың сызықтық кеңістігін құрайды. Осыған байланысты дискретті сигналдар мен дискретті жүйелер теориясының аппараты аналогты сигналдар мен жүйелер теориясының аппараты сияқты егжей-тегжейлі әзірленген, және оған көп жағдайда ұқсас. Разрядтардың саны шектеулі кодтармен ұсынылатын цифрлық сигналдар қосу және көбейту операцияларын орындау кезінде асыра орындау салдарынан желілік кеңістікті құрмайды. Сондықтан дискретті сызықты жүйелердің теориясын қолдану кезінде сандық сигналдарды өңдеуді сипаттау үшін сандардың шектеулі сандар санымен көрсетілуінің әсерін ескеретін модельдерді енгізу қажет.
Сандық өңдеудің ең басты міндеті - кедергілер мен шуылдарды жою. Егер сигнал нақты анықталған параметрлермен артық түссе, бұл тапсырманы толық түрде шешуге болады.
Нәтижесінде сигналдың дұрыс қабылдануын қамтамасыз ету қажет. Пайдалы сигнал неғұрлым көп түскен сайын және кедергілер аз болған сайын, тапсырманы сапалы орындау ықтималдығы соғұрлым көп болады.
Сигналды сандық өңдеудің негізгі міндеттеріне жатады:
* спектрлік таңдау;
* сызықтық сүзу;
* дәстүрлі түрдегі өңдеу,
* жиіліктік уақытша талдау;
* сызықтық емес өңдеу;
* адаптивті сүзу;
* көп жылдамдықты өңдеу;
* секциялық өңдеу.
Сандық өңдеу келесі салаларда қолданылады:
* ұшақ құрастыру, қорғаныс жүйелері, ғарыштық жабдықтар;
* автомобильдерге арналған электроника;
* жарықтандыру жүйелері;
* ұялы, стационарлы байланыс, интернет-телефония;
* үйге арналған электронды аспаптар мен құрылғылар;
* медициналық жабдықтар;
* өлшеуіш және өзге де аспаптар;
* басқару жүйелері;
* қауіпсіздікті қамтамасыз етуге арналған құралдар.
Сигналдарды цифрлық өңдеу кезінде бұрын қолданылған аналогтық әдістерге қарағанда, бүгінгі күні сұраныс әлдеқайда жоғары әр түрлі әдістер қолданылады.
Көптеген әдістердің негізінде DSP-процессорларды қолдану жатыр. Бұл импульсті цифрлық құрылғылар сигналдардың сапалы өңделуін қамтамасыз етеді және дискретті басқару жүйелеріне біріктіріледі.
Сандық өңдеуде қолданылатын әдістер мен алгоритмдер үнемі жетілдіріледі.
Сандық өңдеу бірқатар артықшылықтары бар:
* сигналды өңдеу 75% және одан жоғары дәлдікпен жүргізіледі;
* тұрақсыздандыратын факторлар барынша азайтылады;
* ақпаратты өңдеу бағдарламалық құралдармен жүргізілуі мүмкін.
Сигналды сандық өңдеу бізді күн сайын күнделікті өмірімізде жан-жақты қоршап тұрады. Бұндай өңдеудің нәтижелерін әрбір адам көріп, байқайды, дегенмен көптеген әдеттегі заттарды жүзеге асыру үшін қандай күрделі есептеу жүйелері пайдаланылатынын аңғармайды.
ССӨ пайдалану мысалдары:
* аудиожазбалар мен бейнелерге арналған шуды басу жүйелері;
* суреттерді өңдеу-жарықтандыру деңгейін тегістеу, қарсы алиасинг, псевдотондау салу;
* түрлі көркем әсерлер және суреттер, фотосуреттер және т. б. эстетикалық сапасын жақсарту тәсілдері;
* суретті қалпына келтіру жұмыстары;
* графикалық файлдарда белгілі бір фрагменттерді іздеу;
* суреттер компрессиясы.
Сонымен қатар, сигналдарды сандық әдіспен өңдеу графикада қолданылады, бірақ дыбысты дәл және дұрыс жасай отырып, өңдеу көмегімен шудан тазартуға болады.

Бұл әдіс туралы әлемге бірінші адам француз математигі Жан Батист Жозеф Фурье болды. Фурье жылуөткізгіштік механизмін түсіндіру үшін өзінің математикалық әдісін қолданды. Есептеу қиындықтары туындамайтын ыңғайлы мысал-жылуды Зәкір сақинасы бойынша тарату болып табылады. Отқа батырылған сақинаның бөлігі қызған кезде оны оттан алып тастайды. Жылу ауаға кетіп қалмау үшін сақина дереу ұсақ құмға қазып, содан кейін оның тікелей отпен қызбаған бөлігіндегі температураны өлшейді. Алдымен температураның таралуы тұрақты емес: сақинаның бір бөлігі біркелкі суық, екінші бөлігі біркелкі ыстық, ал осы аймақтардың арасында температураның күрт өзгеру градиенті байқалады. Алайда, жылу ыстық аймақтан суық аймақақ тарайды, температураның таралуы біркелкі болады. Көп ұзамай таралу синусоидалды формаға ие болады: температураның өзгеру кестесі баяу өседі және синус немесе косинус функциясы өзгеретін заң бойынша S әрпі түрінде жойылады. Синусоида біртіндеп тегістеледі және соңында барлық сақина бойынша температура бірдей болады.
Фурье бастапқы тұрақты емес таралуын әр түрлі қарапайым синусоидке бөлуге болады деп болжады, олардың әрқайсысы өзінің ең жоғары температурасы мен фазасы бар, яғни сақинадағы бастапқы жағдайы секілді болады деген. Бұл ретте әрбір синусоидальды компонент максимумнан минимумға өзгеруі тиіс және кері бүтін сан сақина бойынша бір толық айналымда бір рет өзгеруі тиіс. Сақинада бір кезеңі бар құрамдас бөлік басты гармоника деп аталды, ал екі, үш және одан да көп кезеңдер -- тиісінше екінші, үшінші және т.б. гармоника. Ең жоғары температура мен позицияны немесе фазаны сипаттайтын математикалық функция, әр гармоникада температураны үлестіру функциясынан Фурье түрлендіру деп аталады.
Бұл анализді сақина бойынша жылудың таралу процесіне қолдана отырып, Фурье синусоидальды компоненттегі кезеңдердің саны неғұрлым көп болса, соғұрлым ол тез өшуі тиіс деген тұжырымға келді. Бұл ойды температуралық таралудың басты және екінші гармониктері арасында байқалатын қарым-қатынасты бақылай отырып, бейнелеуге болады. Екінші гармоникада температура сақинаның бойымен бір өту кезінде максимумнан минимумға екі рет өзгереді, ал басты гармоникада бұл өзгеріс тек бір рет байқалады. Демек, ең жоғары температурадан ең төменге дейін жылуды жеңу керек қашықтық, екінші гармоникада бірінші, басты гармониядан екі есе аз. Сонымен қатар, екінші гармоникадағы температуралық градиент бірінші гармонияға қарағанда екі есе үлкен. Осылайша, екі есе қарқынды жылу ағыны екі есе аз қашықтықта өтеді, екінші гармоника уақыт функциясы ретінде бірінші қарағанда төрт есе жылдам өшуі тиіс.
Фурье ұсынған тәсілде негізгі қарсылық - шын мәнінде үзілу функциясы үздіксіз болып табылатын синусоидальдық функциялардың жиынтығы болуы мүмкін деген тұжырым. Дегенмен, жылдар өте Фурьенің жасаған тұжырымы математикалық анализдің негізін қалаған және оның дамуына үлес қосқан тұжырым ретінде қабылданды.
Сигналдарды цифрлық өңдеу сигналдардың дискретті түрлендірулерімен және жүйенің осы сигналдарын өңдейді. Дискретті түрлендірулер математикасы 18 ғасырда қатарлар теориясы және оларды интерполяция және функциялардың аппроксимациясы үшін қолдану шеңберінде аналогтық математиканың негізінде пайда болды, алайда ол алғашқы есептеуіш машиналар пайда болғаннан кейін 20 ғасырда жедел даму жолына түсті. Жаплылама алғанда, өзінің негізгі ережелерінде дискретті түрлендірулердің математикалық аппараты аналогтық сигналдар мен жүйелердің түрлендірулеріне ұқсас. Алайда, деректердің дискреттілігі осы факторды есепке алуды талап етеді және оны елемеу елеулі қателіктерге әкелуі мүмкін. Сонымен қатар, дискретті математиканың бірқатар әдістерінің аналитикалық математикада баламасы жоқ.
Фурье дискретті түрленуі (ФДТ) - ғылым мен техниканың әртүрлі салаларында кеңінен қолданылатын сигналдардың спектралды талдауының кең таралған құралдарының бірі. Бұл ретте ССӨ-дің жоғары есептеу тиімділігі үшін көптеген жылдам алгоритмдері әзірленді.
Бұл бөлімде Фурье үздіксіз интегралынан Фурье дискретті-уақыттық түрленуіне және одан әрі Фурье дискретті түрленуіне ерекше назар аударылатын болады.
Қос түрдегі Фурье түрлендіруі келесі түрде болады:

Sω=-infinityinfinitystexp-jωtdt; (19)

st=12PI-infinityinfinitySωexpjωtdω. (20)

мұндағы S(w) - s(t) сигналының спектрі.
Тікелей ФДТ және кері дискретті Фурье (КФДТ) түрлендіру үшін өрнектер төмендегідей болады:

Sdk=n=0N-1snexp-j2PINnk, k=0...N-1; (21)

sn=1Nk=0N-1Sdkexpj2PINnk, n=0...N-1. (22)

ФДТ Sd(k), k=0...N-1 спектрінің есептеулерін s(n), n=0...N-1, N N-ретті сигналдардың есептеулеріне сәйкес қояды. Бұл жерде және одан әрі осы бөлімде айнымалы n сигналдың уақытша есептеуін индекстейді, ал айнымалы k ФДТ спектралды есептеуін индекстейді. Үздіксіз және дискретті жағдайларда кері түрлендіруге арналған өрнектерде нормалаушы коэффициент бар. Фурье интегралы кезінде бұл коэффициент - 12PI, ал КФДТ кезінде - 1N-ге тең.
Нормалаушы коэффициент жиіліктік аймақтан уақытша сигналды дұрыс масштабтау үшін қажет. Нормалаушы коэффициент бастапқы сигналдың амплитудасымен сәйкес келу үшін кері түрлендірудің шығысындағы сигнал амплитудасын азайтады. Егер кейбір сигналдың Фурье тура түрлендіруін тізбектеп есептесе, ал кейін Фурье кері түрлендіруін алса, онда кері түрлендірудің нәтижесі бастапқы сигналмен толық сәйкес келуі тиіс.
Уақыт бойынша сигналды дискреттеу немесе Фурье дискретті-уақытша түрлендіру қарапайым ФДТ қатты ұқсас келеді. Sd(t) дискретті сигналын s(t) үздіксіз сигналын торлы функцияға көбейту нәтижесі ретінде қарастырайық:

Sdt=s(t)n=0N-1δt-n∙∆t=n=0N-1stδ(t-n ∙∆t), (23)

мұндағы δ(t) - дельта - функция:

δt=infinity егер t=0;0 егер t!=0, (24)

∆t - дискретизация интервалы. Дискретизация процесінің графикалық көрінісін 6-суреттен көруге болады.

6-сурет. Сигналды дискретизациялау процессі

Sd(t) дискретті сигналының Фурье түрлендіруін есептейміз, ол үшін s(t) үздіксіз сигналын торлы функцияға көбейтіндісін Фурье түрлендіруге арналған өрнекке қоямыз:

Sdω=-infinityinfinitysdtexp-jωtdt=- infinityinfinityn=0N-1stδt-n∙∆texp- jωtdt. (25)

Қосылым және интегралдау операциясының орнын өзгертеміз және дельта-функцияның сүзгілеуші қасиетін қолданамыз:

-infinityinfinitystδt-τdt=st. (26)

Жоғарыдағы өзгерістерді ескерсек, Фурье түрлендіру төмендегідей көріністе болады:

Sdω=n=0N-1-infinityinfinitystδt-n∙∆ texp-jωtdt=n=0N-1sn∙∆texp-jω∙n∙∆t. (27)

Осылайша, біз шексіз шектерде интегралданудан құтылып, оны кешенді экспоненттің соңғы жиынтығымен алмастырдық. Мұндағы exp⁡(-jω∆t) кешенді экспоненттері Ohm(n) периодты функция болып табылады:

Ωn=2PIn∙∆t=2PI∙n∙Fs,радс, n=1...N-1, (27)

Бұл жерде Fs=1∆t - сигналды дискреттеу жиілігі.
Sd(ω) спектрінің қайталауының максималды кезеңі n = 1 кезінде болады, бұл жағдайда ол:

Ωmax=Ω1=2PI∆t=2PI∙Fs. (28)

Осылайша, Sd(t) дискретті сигналдың Sd(ω) спектрі 2PI∙Fs - ге, ω циклдік жиілігі бар периодтық функцияға тең. Егер дискретизация жиілігін Fs=1 шамасына жеткізетін болсақ, Фурье түрлендіруі дискретті-уақыт бойынша Фурье түрлендіруге келеді:

Sωн=n=0N-1snexp-jωнn. (29)

Цифрлық өңдеу алгоритмдерін бағдарламалық жүзеге асыру үшін сигналдың дискретті есептеулері, сондай-ақ спектрдің дискретті есептеулері талап етіледі. Дискретті немесе сызықтық спектрдің периодтық сигналдары бар екені белгілі. Бұл жағдайда дискретті спектр периодтық сигналдың Фурье қатарына жіктеу арқылы алынады. Сондықтан, дискретті спектрді алу үшін, кейбір кезеңмен бір рет шексіз мөлшерде осы сигналды қайталаудың периодты жолымен бастапқы дискретті сигнал жасау керек. Ол кезде периодтық сигнал спектрі ∆ω=2PIT дискретті тербелістерді қамтиды. Уакыт бойынша сигналдың қайталануы графикалық процесі 7-суретте көрсетілген.

7-сурет. Сигналдың уақыт бойынша қайталануы

Қара түспен бастапқы сигнал белгіленген, ал қызыл түспен оның кейбір периодтан кейін қайталануы көрсетілген. Сигналды әр түрлі Т периодпен қайталауға болады, алайда, сигнал мен оның қайталануы бір уақытта қабаттаспауы үшін, қайталану периоды сигнал ұзындығына тең немесе үлкен TN∙∆t болуы керек. Бұл ретте, сигнал мен қайталанудың бір-біріне қабаттаспайтын, минималды қайталану периоды Tmin төмендегідей формуламен есептеледі:

Tmin=N∙∆t, сек. (30)

8-сурет. Сигналдың минималды периодпен қайталануы

Жылдам Фурье дискретті түрленуі-тізбектің дискретті түрленуін немесе оның кері түрленуін есептейтін алгоритм. ФДТ мәндердің реттілігін әр түрлі жиіліктердің компоненттеріне бөлу жолымен алынады. Бұл әдіс көптеген салаларда пайдалы, дегенмен, оның есептеу жылдамдығы салыстырмалы түрде төмендеу болды. Бұл мәселені Фурье дискретті тез түрленуі шештіү Аталмыш әдіс матрицалық есептеу негізінде жұмыс жасайды және түрлендіру уақытын айтарлықтай азайтады.
Фурье терезелік түрлендіруі - қарапайым Фурье дискерттік түрлендіруі сигналдың спектралдық құрамының жылдам уақыт кезінде оның локалдық қасиеттері мен жиіліктік ақпараттарын толық сипаттай алмайтын жағдайларда қолданылады. Сигналдың уақыт интервалы ұзақ болған кезде ол интервал подинтервалдарға бөлінеді және Фурье түрлендіруі әрбір подинтервал үшін жеке-жеке ретімен орындалады. Терезелік түрлендіру келесі өрнек бойынша орындалады:

Sω,bk=-infinityinfinityst∙ω(t-bk)∙e -jωtdt. (31)

ФДТ алгоритмдері көптеген салаларда кеңінен қолданысқа ие әдістердің бірі. Фурье дискретті түрлендіруі, инверстелген Фурье түрлендірген, жылдам Фурье дискретті түрлендіруі немесе басқа да алгоритмдердің барлығы нақтыланған бір салаларда кеңінен қолданылады:
* Спектралды анализ - физика, математика салаларында жиілік бойынша дыбыстық немесе өзге де сигналдарды спектралды тығыздығы бойынша зерртеу;
* Ақпараттардың көлемін қысу - аудио-файл, сурет секілді ақпараттардың көлемін азайту барысында ФДТ арқылы файлды сегменттерге бөліп, байқалмайтын бқліктер алынып тасталынады.
* Полиномдарды көбейту - көпмүшелік полиномдарды өзара көбейту жылдамдығын арттыру үшін Фурье дискретті түрлендіру алгоритмдері қолданылады.
Фурье дискретті түрлендірудің қасиеттері:
* Сызықтық қасиеті. Сигналдар қосындысының спектрі осы сигналдардың спектрлерінің жиынтығына тең. Егер s(n) = x(n) + y(n) болса, S(k) келесідей болады: S(k) = X(k) + Y(k);
* Уақыт осі бойынша жылжыту қасиеті. s(n) сигналының S(k) спектрі болады. Егер s(n) сигналды m циклдік қадамға жылжытсақ, яғни x(n)= s(n-m), онда жылжыған сигналдың спектрі: Xk=n=0N-1s(n-m)∙WNn∙k. Осылайша, сигналды m циклдік қадамға жылжыту оның фазалық спектрінің жылжуына әкеледі, бірақ та амплитудалық спектрі өзгермейді;
* Кіріктірілген циклдің сигналдардың Фурье дискретті түрлендіруі. Сигнал s(n) a(n) және b(n) сигналдарының циклдік кіріктірілуінің қорытындысы болсын: sn= m=0N-1a(m)∙b(n-m). Бұл сигналдың спектрі есептейік: Sk=n=0N-1m=0N-1a(m)∙b(n-m)∙WNn∙k. Мұндағы жинақтау операцияларының орнын ауыстырсақ: S(k) = B(k) ∙ A(k). Яғни, сигналдарының циклдік кіріктірілуінің спектрі осы сигналдардың спектрлерінің көбейтіндісіне тең;
* Екі сигналдың көбейтіндісінің спектрі. Бұл жерде алдыңғы қасиетке кері амалдар орындалады. Яғни, сигналдардың көбейтіндісінің спектрі осы сигналдардың циклдік кіріктірілуінің спектріне тең болады;
* Спектрдің ауысуы сигналды кешенді экспонентке көбейту арқылы жүзеге асырылады. Кешенді экспонентке көбейтілгеннен кейін сигнал кешенді болады, ал оның спектрі симметриялы емес болады;
* Нақты сигнал спектрінің инверсиясы. Сигнал спектрін инверсиялау үшін сигналдың әрбір екінші есебін минус бірлікке көбейту жеткілікті. Бұл ретте жұп санаудың бірлігіне минус көбейту спектрдің спектральды санаудың n2-ге оңға циклдық ығысуына сәйкес келеді, ал тақ санауыштарды көбейту санаудың N2-ге спектрдің солға циклдық ығысуына сәйкес келеді.

1.2. Цифрлық сигналдарды вейвлет түрлендіру
Сигналдарды Вейвлет түрлендіру спектралды талдаудың жалпылама түрі болып табылады, оның қарапайым өкілі - Фурьенің классикалық түрлендіруі. Вейвлет термині ағылшын тілінен аударғанда қысқа толқын деген мағынаны білдіреді. Вейвлеттер-бұл белгілі бір формадағы математикалық функциялар тобының жалпыланған атауы, олар уақыт пен жиілік бойынша жергілікті және барлық функциялар бір базалық негіз арқылы уақыт осі бойынша жылжу мен созылу арқылы алынады. Вейвлет түрлендірулер уақыт пен жиілік бойынша локализацияланған тербелістер терминдеріндегі талданатын уақыттық функцияларды қарастырады. Әдетте, вейвлет түрлендірулер дискретті және үздіксіз болып бөлінеді.
Дискретті вейвлет түрлендіру сигналдарды түрлендіру және кодтау үшін, үздіксіз вейвлет түрлендіру - сигналдарды талдау үшін қолданылады. Вейвлет түрлендіру молекулалық динамиканы, кванттық механиканы, астрофизиканы, геофизиканы, оптиканы, компьютерлік графиканы және бейнелерді өңдеуді, ДНҚ талдауын, жасушаларды зерттеуді, климатты зерттеуді, сигналдарды жалпы өңдеуді және сөйлеуді тануды қоса алғанда, көптеген салаларда қолданылады.
Вейвлет талдауы табиғи орта мен объектілердің процестері мен физикалық қасиеттері туралы физикалық деректерді осы сигналдармен бейнелейтін сигналдардың сызықтық түрленуінің ерекше түрі болып табылады. Сигналдардың вейвлеттік ыдырауы жүргізілетін өзіндік функциялардың базисі көптеген ерекше қасиеттерге және мүмкіндіктерге ие. Базистің вейвлеттік функциялары Фурье мен Лапластың дәстүрлі түрлендірудің көмегімен анықталуы мүмкін емес талданатын процестердің сол немесе басқа жергілікті ерекшеліктеріне назар аударуға мүмкіндік береді. Геофизикадағы мұндай процестерге табиғи ортаның түрлі физикалық параметрлерінің өрістері жатады. Бірінші кезекте бұл температура, қысым өрістеріне, сейсмикалық трассалардың бейініне және басқа да физикалық шамаларға қатысты. Вейвлеттерді уақыт немесе кеңістікте компоненттік мазмұнның өзгеруімен стационарлы емес сигналдарды талдау мүмкіндігі принципті мәнге ие.
Вейвлеттерде нөлдік интегралды мәні бар қысқа толқынды пакеттердің түрі бар, олар аргументтердің осі бойынша оқшауланған, жылжытуға инвариантты және масштабтау операциясына ыңғайланған. Вейвлеттер уақытша және жиілік көрінісінде локализациясы бойынша жиілік бойынша локализацияланған гармоникалық функциялар мен уақыт бойынша локализацияланған Дирак функциясы арасынан аралық орын алады.
Вейвлеттер теориясы негізгі теория емес, бірақ ол көптеген практикалық міндеттерді шешу үшін ыңғайлы және тиімді құрал бола алады. Вейвлетті түрлендірулерді қолданудың негізгі саласы-уақыт бойынша стационарлық емес немесе кеңістікте біртекті емес сигналдар мен функцияларды талдау және өңдеу, талдау нәтижелері сигналдың жалпы жиіліктік сипаттамасын ғана емес, сонымен қатар жиіліктік құрамдастардың белгілі бір топтары көрсететін немесе сигналдың жиіліктік құрамдастарының жылдам өзгерістері болатын белгілі бір жергілікті координаттар туралы мәліметтерді қамтуы тиіс. Сигналдардың Фурье қатарына ыдырауымен салыстырғанда вейвлеттер сигналдардың жергілікті ерекшеліктерін неғұрлым жоғары дәлдікпен көрсете алады. Сонымен қатар, бұл жағдайда жиілік пен координаталар тәуелсіз айнымалылар ретінде қарастырылады, бұл бірден екі кеңістіктегі сигналдарды талдауға мүмкіндік береді.
"Вейвлет" терминінің өзі түсінік ретінде 1984 жылы жарияланған J.Morlet және A. Grossman мақаласында енгізілді. Олар вейвлет деп аталатын базис көмегімен сейсмикалық сигналдарды зерттеумен айналысты. Бұл жұмыс кейінгі он жыл ішінде бірқатар авторлардың вейвлеттерін дамытуға бастама берді. Вейвлеттер теориясына үздіксіз вейвлет түрлендіру негізін қалыптастырған Гуппилауд, Гроссман және Морлет, дискретті вэйвлеттер бойынша жұмыс жасаған Жан Олаф-Стромберг, ортогональды вейвлеттерді әзірлеген Дрид Добеши, үздіксіз вейвлет түрлендірудің уақыттық-жиілік интерпретациясын жасаған Натали Делпрат, гармоникалық вейвлет-түрлендіруді әзірлеген Ньюланд және т.б. салмақты үлес қосты. Қазіргі уақытта вейвлеттер бойынша кеңейтулердің арнайы пакеттері компьютерлік математиканың негізгі жүйелерінде(Matlab, Mathematica, Mathcad және т. б.) бар, ал вейвлет-түрлендірулер мен вейвлет анализі әртүрлі есептерге арналған Ғылым мен техниканың көптеген салаларында қолданылады: бейнелерді тану, күрделі сызықты емес процестердің динамикасын сандық модельдеу, медицинадағы, ғарыштық техникадағы, астрономиядағы, геофизикадағы аппараттық ақпарат пен бейнелерді талдау, сигналдарды тиімді қысу және өткізу қабілеті шектеулі арналар және т.б. қолданылады. Көптеген зерттеушілер вейвлет-талдауды біртекті емес сигналдар мен функциялардың ішкі құрамы мен құрылымдарын дәл зерттеуше арналған "математикалық микроскоп" деп атайды. Вейвлет-сигналдарды өңдеу және талдау әдістерін кез келген міндеттерді шешу үшін жаңа әмбебап технология ретінде қарастырмаған жөн. Вейвлеттердің мүмкіндіктері әлі толық ашылмаған. Алайда, бұл олардың дамуы болашақта жақсы өңделген және уақытпен сыналған дәстүрлі ақпаратты өңдеу және талдау құралдарын толық ауыстыруға әкеледі дегенді білдірмейді. Бірақ ол деректерді өңдеудің ақпараттық технологияларының аспаптық базасын едәуір кеңейте алады.
Фурье түрлендіруінің гармоникалық базистік функциялары жиілік аймағында шектік оқшауланды және уақыт интервалында оқшауланбаған. Оларға қарама-қарсы уақыт аймағында шектік оқшауланған және барлық жиілік диапазоны бойынша "біркелкі емес" орналасқан Кронекер импульстері түріндегі импульстік базистік функциялар болып табылады. Осы екі функциялардың локализация бойынша вейвлеттерді гармоникалық және импульстік функциялар арасында аралық орын алатын функциялар ретінде қарастыруға болады. Олар түрлендірудің уақыт және жиілік аймағында оқшаулануы тиіс. Бірақ мұндай функцияларды жобалау кезінде біз функциялардың ұзақтылығы мен олардың спектрінің енінің тиімді мәнін байланыстыратын белгісіздік қағидатына бетпе-бет келеміз. Функцияның уақыт аймағында оқшаулауды дәлірек жүргізген сайын, оның спектрі соғұрлым кең болады. Вейвлет-талдаудың ерекше ерекшелігі, онда белгісіздік арақатынасының түрлі нұсқаларын іске асыратын функциялар тобын пайдалануға болады. Тиісінше, зерттеуші олардың арасында икемді таңдау жасап және қойылған міндеттерді неғұрлым тиімді шешетін вейвлет функцияларын қолдану мүмкіндігіне ие. L2(R), R(-infinity,infinity) кеңістігінің вейвлет базисі осы кеңістікке тиесілі финиттік функциялардан құрастырылғаны жөн және олар шексіз нөлге ұмтылуға тиіс. Бұл функциялар нөлге жылдамырақ ұмтылған сайын, оларды нақты сигналдарды талдау кезінде түрлендіру базисі ретінде пайдалану ыңғайлырақ болады. Мысалы мұндай функция ретінде кейбір соңғы интервалдан тыс нөлге тең және тапсырма интервалы бойынша нөлдік орташа мән болып табылатын - ψ(t) psi-функциясы. Тапсырма интервалы бойынша нөлдік орташа мән жиілік аймағында вейвлет спектрін белгілі бір оқшаулауды белгілеу үшін қажет. Осы функцияның негізінде тәуелсіз айнымалыны ауқымды түрлендірулер көмегімен L2(R) кеңістігінде базис құрастырамыз.
Сигналдардың спектрлік көрінісінде тәуелсіз жиілікті айнымалы өзгерту функциясы сигналдың созылусығылуының уақыт аймағы көрінісінде көрсетіледі. Вейвлет базисі үшін мұны ψt⟹ψamt, a=const, m=0, 1,...M функциясымен орындауға болады, яғни әр түрлі масштабта өзіндік функцияларды қамтамасыз ететін созылусығылу сызықтық операциялары арқылы. Дегемен, ψ(t) функциясының уақыт осі бойынша түпкілігі R(-infinity,infinity) кеңістігінің барлық сандық осін жабу үшін ψ(t) функциясының ось бойымен ψt⟹ψ(t+k) секілді қосымша тәуелсіз ауыспалы тізбекті тасымалдарын талап етеді. Екі шартты бір мезгілде ескере отырып, базистік функцияның құрылымы келесідей болуы мүмкін:

ψt⟹ψamt+k. (32)

M және k айнымалы мәндерін одан әрі есептеуді оңайлату үшін бүтін санмен байланыстырамыз. Жоғарыда көрсетілген формуланы бірыңғай нормаға келтірсек:
ψmkt=am2ψamt+k. (33)

Егер ψmkt функциялар тобы үшін ортогональ шарты орындалса:

ψnkt,ψlm(t)=-infinityinfinityψnkt∙ψ nk*tdt=δnl∙δkm, (34)

бұл жағдайда L2(R) кеңістігінің ортонормаланған базисі ретінде ψmkt функциялар тобы пайдаланылуы мүмкін. Демек, бұл кеңістіктің еркін функциясы қатар түрінде ұсынылуы мүмкін:

st=m,k=-infinityinfinitySmk∙ψmk(t), ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.