Бір фазалы синусоидалы ток тізбегі: синусоидалы токтың қасиеттері, әрекеттік мәндер және кешендік (фазалық) талдау


Бір фазалы синусоидалы тоқтың электр тізбегі
Синусоидалы (айнымалы) тоқ деп синус зандылығы мен өзгеретін тоқты айтады:
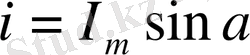
Айнымалы тоқтың тұрақты тоққа қарағанда ерекшелігі, оны алыс қышықтықтарға қарапайым айнымалы тоқ генератор құрылғысы мен қажетке пайдаланғанда сенімділігі жоғары қозғалтқыштары бар трансформаторлық қосалқы станцияларды пайдалана отырып, тарата алады. Электр магниттік ЭҚК шамасы магнит индукциясынан В, сымның активті кедергісінен l, өткізгішті қиып өтетін магнит күштік сызықтардың жылдамдығына V және магнит индукциясының векторы мен жылдамдықтың векторының бағытарының арасындағы синус бұрышынан тәуелді болады. Электр магнитті ЭҚК - i келесі формуламен анықталады:
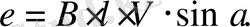
Электр магниттік индукцияның ЭҚК - нің a - дан тәуелділігін қарастырамыз:

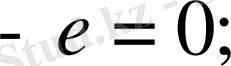

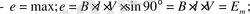
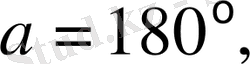

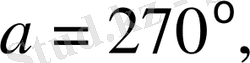

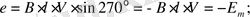


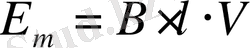 ден белгілей отырыпб электр магниттік индукцияның ЭҚК анықтау формуласы төмендегідей болып анықталады:
ден белгілей отырыпб электр магниттік индукцияның ЭҚК анықтау формуласы төмендегідей болып анықталады:
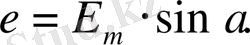
Егер рамканы кедергімен тұйықтаса, онда рамка мен кедергінің бойымен синус зандылығымен өзгеретін тоқ өтеді:
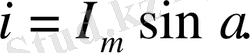
Бұрыштық жиілік
 уақыт бірлігінде рамканың бұрылу бұрышына тең:
уақыт бірлігінде рамканың бұрылу бұрышына тең:
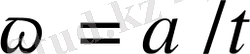 немесе
немесе

Осы қатынасты есепке ала отырып, тоқтың қисығын пайдалана отырып, айнымалы тоқтың негізгі ұғымдарын анықтаймыз.

Мұндағы
i
- тоқтың лездік мәні,
A;
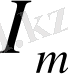 - тоқтың максимал мәні,
- тоқтың максимал мәні,
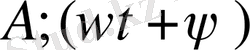 - берілген уақыт ішіндегі
t
тербелістің күйін сипаттайтын фаза;
- берілген уақыт ішіндегі
t
тербелістің күйін сипаттайтын фаза;
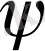 - бастапқы фаза.
- бастапқы фаза.

Период Т - бұл тоқтың толық өзгеруіне кететін уақыт, секундпен өлшенеді.
Периодқа кері шаманы
жилік
f
деп атайды, жилік
герцпен
өлшенеді. Бұрыштың градустағы өлшем бірлігінің орнына радианды қолдануға болады.
Радиан
деп доғасы радусқа тең бұрышты айтады. Шеңбердің ұзындығы
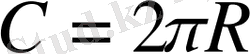 тең болғандықтан, 360° толық бұрышқа
тең болғандықтан, 360° толық бұрышқа
 радиан сәйкес келеді. 360° периодқа Т сәйкес келеді. Осы қатынасты пайдалана отырып, циклдік жиілікті
f
бұрыштық жиіліктің формуласын табыныз.
радиан сәйкес келеді. 360° периодқа Т сәйкес келеді. Осы қатынасты пайдалана отырып, циклдік жиілікті
f
бұрыштық жиіліктің формуласын табыныз.
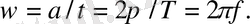
Синусоидалы тоқтың орташа мәні жарты периодпен анықталады:
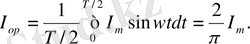
ЭҚК - тің және кернеудің орташа мәндері де дәл осылай табылады:
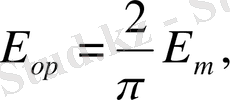
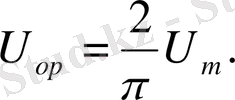
Синусоидалы тоқтың әрекеттік мәні жылулық эффектпен бағаланады. Айнымалы тоқпен өндірілген жылулық әсерді бағалау үшін, оны тұрақты тоқтың жылулық әсерімен салыстыруы керек. Бұл үшін бір кедергіде R алдымен тұрақты тоқты, сонан соң айнымалы тоқты жібереміз және Т периодқа тең уақытта бөлініп шыққан жылу мөлшерін теңдестіреміз. Жылу мөлшері Джоуль - Ленц формуласымен анықталады.
Тұрақты тоқ үшін жылу мөлшері (Q) келесі формуламен анықталады:
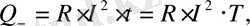
Мұндағы
 - кедергіде
R
бөлініп шығатын жылу мөлшері; I
-
кедергінің R бойымен ағатын тоқ; t - кедергінің R бойымен тоқ өткендегі уақыт.
- кедергіде
R
бөлініп шығатын жылу мөлшері; I
-
кедергінің R бойымен ағатын тоқ; t - кедергінің R бойымен тоқ өткендегі уақыт.
Тұрақты тоқ үшін жылу мөлшері (Q) келесі формуламен анықталады:

Q_= Q - болғандықтан
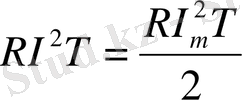
Осыдан:
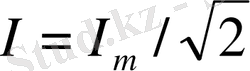
Мұндағы I - айнымалы тоқтың әрекеттік мәні.
Синусоидалы тоқтың әр түрлі көрсетілу тәсілдері (түрлері)
Синусоидалы тоқтың көрсетілулерінің негізгі үш тәсілі бар: тригонометриялық, графикалық және кешендік жазықтықта бейнеленуі.
1. Тригонометриялық тәсілде бейнеленуі:
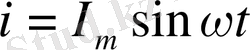
2. Графикалық тәсілде бейнеленуі:
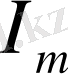
3. Кешендік жазықтықта бейнеленуі:
Кешендік жазықтықта синусдалы тоқтардың векторларының бірдей болып бейнеленуі мақсатында уақыт кезенің
 тең деп алу қабылданған.
тең деп алу қабылданған.
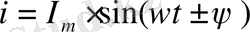 тоғының көрсеткіштік түрін Эйлер формуласын пайдалана отырып, анықтауға болады:
тоғының көрсеткіштік түрін Эйлер формуласын пайдалана отырып, анықтауға болады:
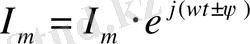
немесе
 болғанда:
болғанда:

мұндағы
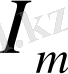 - айнымалы тоқтың көшендік мәні;
- айнымалы тоқтың көшендік мәні;
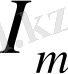 - модулі;
- модулі;
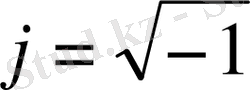 - жорамал мәні.
- жорамал мәні.
Тоқтың көшенді шамасының жазылу үлгісін қарастырамыз.
Тригонометриялық түрдегі жазылуы:
1.
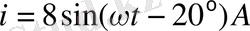
Кешендік түрдегі жазылуы:
2.
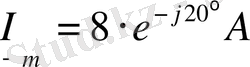
Кешендік жазықтықта айнымалы тоқтың векторының бейнелену төмендегідей болады:


Кешендік жазықтықта бір жиілікте уақыт функциясында синусоидалы өзгеріп бейнеленген және олардың фаза бойынша (
 бұрышы) бір - бірінен сәйкестеліп тұрғызылған векторлардың жиынтығы
векторлық диаграмма
деп аталады. Барлық векторлардың бір бұрышқа бір мезгілде бұрылуы олардың өзара орналасуын өзгертпейді, осыдан
бастапқы вектор
деген ұғымды алуға болады.
бұрышы) бір - бірінен сәйкестеліп тұрғызылған векторлардың жиынтығы
векторлық диаграмма
деп аталады. Барлық векторлардың бір бұрышқа бір мезгілде бұрылуы олардың өзара орналасуын өзгертпейді, осыдан
бастапқы вектор
деген ұғымды алуға болады.
Бастапқы вектор деп кешендік жазықтықта +1 осымен сәйкес келетін векторды айтады.
Кирхгофтың заңдарының кешендік түрлері
Кирхгофтың заңдарының кешендік түрде келесі түрде жазылады:
Кирхгофтың бірінші заңы:
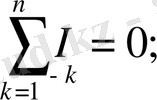
Кирхгофтың екінші заңы:
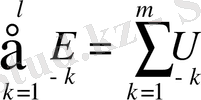
Синусоидалы тоқ тізбегіндегі активті, индуктивті, сыйымдылықты кедергілер
Синусоидалы тоқ тізбегіндегі активті кедергі
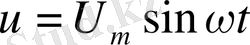 кернеу беріледі, осы кернеудің әсерінен тізбектің бойымен тоқ жүреді:
кернеу беріледі, осы кернеудің әсерінен тізбектің бойымен тоқ жүреді:

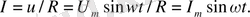
Активті кедергіде тоқ пен кернеу фаза бойынша сәйкес (бағыттас) болады. Фазасы бойынша сәйкес келуі векторлық диаграммада және уақыттық диаграммада көрсетілген.
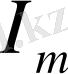
Кедергідегі тоқ пен кернеудің әрекеттік мәндері кешендік түрде келесі түрде жазылады:
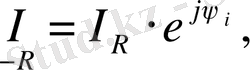

Бұл тізбек үшін Ом заңының кешендік түрі төмендегідей жазылады:
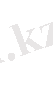
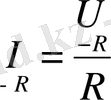
Синусоидалы тоқ тізбегіндегі индуктивтілік. Айнымалы тоқ, өткізгіш арқылы өте отырып, айнымалы магнит ағынын тудырады. Бұл кезде тұйықталған орамда өздік индукцияның ЭҚК туады. Өздік индукцияның ЭҚК - i келесі формула бойынша анықталады:
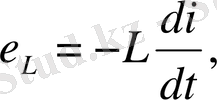
мндағы L - индуктивтілік деп аталатын коэффициент.
Индуктивтілік генримен (
Г
 ) өлшендеді.
) өлшендеді.
l А/с тоқтың өзгеру жылдамдығында өзара индукцияның ЭҚК - i l вольт туындатқанда электр тізбекінің l
Г
 индуктивтілігі болады
.
индуктивтілігі болады
.
Индуктивтілігі бар схеманы қарастырамыз.
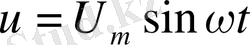 кернеу беріледі, осы кернеудің әсерінен тізбектің бойымен тоқ жүреді:
кернеу беріледі, осы кернеудің әсерінен тізбектің бойымен тоқ жүреді:
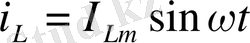
Индуктивтіліктің орауышында өздік индукция ЭҚК - i тудырылады.
Индуктивтіліктің орауышындағы кернеу келесі формуламен анықталады:
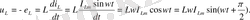
 деп белгілейміз,
деп белгілейміз,
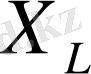 индуктивтілікті кедергі
деп айтылады. Индуктивтілікте кернеу тоқтан 90° - қа (
индуктивтілікті кедергі
деп айтылады. Индуктивтілікте кернеу тоқтан 90° - қа (
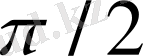 ) озып отырады.
) озып отырады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz