ЖЕРДІҢ ПІШІНІ МЕН ӨЛШЕМІ ТУРАЛЫ ЖАЛПЫ ТҮСІНІК

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министрлігі

Әл - Фараби атындағы Қазақ Ұлттық Университеті

Факультеті: «География және табиғатты пайдалану»

Кафедрасы: «Кадастр және жерге орналастыру»

РЕФЕРАТ

Тақырыбы: Жердің пішіні және өлшемі туралы тағы

да оларды анықтау әдістері

Орындаған: Қапидолла Д. Т

Тексерген: Құттыбаев А. Е

Алматы, 2021ж

МАЗМҰНЫ:

КІРІСПЕ
Жер. Жердің пішіні мен өлшемі туралы жалпы түсінік
Жер пішінін зерттеу әдістері
ҚОРЫТЫНДЫ
Қолданылған әдебиеттер

КІРІСПЕ

Ғылым мен техниканың көптеген салалары (жердің жасанды серіктері мен арыштық ракеталарды ұшыруда, авиацияда, теңізде жүзу, радиобайланыс, т. б. ), әсіресе жер бетін картада дұрыс кескіндеу, жердің пішіні мен көлемін дәл білуді қажет етеді. Сондықтан адамзат үшін жердің пішіні мен көлемін және оған байланысты барлық түсінікті білу маңызды болып табылады.

ЖЕР. ЖЕРДІҢ ПІШІНІ МЕН ӨЛШЕМІ

ТУРАЛЫ ЖАЛПЫ ТҮСІНІК

Жер - күн жүйесіндегі планеталардың бірі. Оның жалпы ауданы 510 млн. кв. км-ге тең. Жер қыртысы әртүрлі қыраттар мен ойпаттардан тұрады. Жердің шамалы ғана бөлігін 29 % құрылық, ал 71 % дүние жүзілік мұхит сулары алып жатыр. Мұхит әлемінің орта тереңдігі - 3800 м болса, құрылықтың мұхит суларының орташа деңгейінен орташа биіктігі - 875 м-ге жуық. Жоғарыда көрсетілген шамалар құрылық бетінің аумағы жалпы жер бетінің аумағынан, ал оның биіктігі мұхиттың тереңдігінен біршама аз екенін көрсетеді. Сол себептен жер беті үшін шамамен дүние жүзілік мұхит және теңіз суларының тыныш жағдайына сәйкес келетін деңгей беті алынады. Құрылық астын ойша жүргізілген мұндай бет тұйық фигура жасайды және кез-келген нүктесінде жердің ауырлық күшіне бағытталған тіктеуіш сызықтарды тік бұрыш жасап қиып өтеді. Яғни мүндай түйық беттің кез-келген нүктесі ауырлық күшінің бағытына перпендикуляр. Осы деңгей бетпен шектелген денені-геоид деп атайды. Геоид-гректің ge-«жер» және daio-«бөлу» деген сөздерінен алынган. Геоидтың пішіні күрделі, оның пішіні мен көлемін дәлірек анықтау үшін, жер бетінің барлығына өлшеулер жүргізіледі. Оны деңгейлік бет деп атайды. Жерді айнала орайтын осындай деңгейлік беттердің саны көп болуы мүмкін. Соның ішінде мұхиттың тыныш күйіндегі орта деңгеймен бірдей келетін деңгейлік бетпен құрайтын пішінді геодезияда Жердің жалпы пішіні немесе геоид деп атайды. Жердің қабаттарында салмақтың біркелкі таралмағына байланысты геоидтың пішіні дұрыс геометриямен сызылмайды, оның беті сол себептен математикалық жүйеге келмейді. Сондықтан да жердің геоид пішінді бетін математикалық бір жүйеге келетін немесе соған жуықтайтын басқа беттермен ауыстырады. Жердің деңгейлік бетін жуықтап белгілі радиусы бар сфера деп алуға болады. Бұған мысал кәдімгі глобус жатады.

Оның шар тәрізді екендігі туралы алғашқы ойлар Пифагор (біздің эрамызға дейін 530 ж. ) мен Аристотельдің (біздің эрамызға дейінгі IV ғ. ) еңбектерінде жазылған. Аристотель Айдың тұтылуын байқау кезінде Жердің Айға түсірген көлеңкесі доға тәрізді болып шектелетіндігіне көңіл аударған.

Геодезиялық өлшеу жұмыстарының нәтижесі Жердің сыртқы пішіні үш осьті эллипсоидқа (сфероид) жақын екендігін көрсетеді. Жердің полярлық радиусы (Кп) - 6356, 8 км, экваториалдық радиусы (Кэ) -6378, 2 км, ал полярлық сығым мөлшері а=(Кэ-Кп) : Кэ-1/298, 2 (Ф. Н. Красовский, А. А. Изотов) . Жердің орташа радиусы 6371, 11 км шамасында деп есептеледі.

Жердің шын мәніндегі бейнесі өте күрделі. Ол ешқандай да геометриялық фигураға ұқсамайды. Сондықтан неміс ғалымы - физик И. Люстихтың (1873 ж. ) ұсынысы бойынша Жер геоид (жерге ғана тән өзіндік пішін) пішінді деп саналады.

Геодезиялық, астрономиялық, гравиметрлік дәл өлшемдер арқылы геоид бетінің пішінін эллипсоид айналуынан пайда болған математикалық беттің пішініне жақын екені анықталады.

Жердің негізгі сызықтары мен жазықтықтары. Жердің өз осінде айналуынан оның бетінде күн мен түн алмасып, күн тәулігі пайда болады. Осы осьті ( сурет 1 ) - жердің айналу осі деп атайды. Бұл осьтің жер бетімен қиылысатын екі нүктесі бар. Олар Солтүстік және Оңтүстік полюстер. Жердің айналу осін тік бұрыш жасап және дәл ортасы арқылы өтетін жазықтықты экватор жазықтығы деп атайды. Экватор жазықтығы мен жер бетінің қиылысу сызығы - экватор деп аталады.

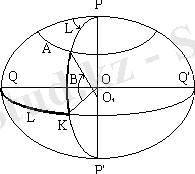$C:\Users\балдаурен\Desktop\Дидар Универ\Без названия.png$ Cурет 1- Геодезиялық координаталар жүйесі

Жердің айналу осі арқылы өтетін жазықтық - меридиан жазықтығы делінеді де, сол жазықтықтың жер бетімен қиылысу сызығы - географиялық меридиан деп аталады. Халықаралық келісім бойынша Лондон жанындағы Гринвич обсерваториясы арқылы өтетін меридиан бастапқы, бірінші немесе нольдік меридиан деп аталады. Экваторлық жазықтыққа параллель жазықтықтардың жер бетімен қиылысу сызықтарын параллельдер деп атайды.

Жердің қабаттарында салмақтың біркелкі таралмағына байланысты геоидтың пішіні дұрыс геометриямен сызылмайды, оның беті сол себептен математикалық жүйеге келмейді. Сондықтан да жердің геоид пішінді бетін математикалық бір жүйеге келетін немесе соған жуықтайтын басқа беттермен ауыстырады. Ондай беттерді екі түрге бөлуге болады.

Жердің деңгейлік бетін жуықтап белгілі радиусы бар сфера деп алуға болады. Бұған мысал кәдімгі глобус жатады.

Бізде орташа деңгей бет үшін Балтық теңізіндегі Кронштад футштогінің нолі алынады, оны Балтық теңізінің деңгей беті деп атайды. Футшток деген мыстан жасалған, көлденең сызықтың тұсына нөл саны көрсетілген тақта.

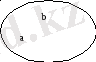
Бүкіл әлемдік тартылыс заңынан алынған әсерінен жер шарға емес, айналу осінің бағытынша сфероидқа ұқсайды. Сөйтіп, геодезияда жердің пішіні ретінде Жер сфероиды алынып, геодезиялық өлшеулердің нәтижелері негізгі деңгей бетке іс жүзінде, жер эллипсоидының бетіне проекцияланады ( сурет 2 ) .

$C:\Users\балдаурен\Desktop\Дидар Универ\Без названия (1).png$ Q Q ₁

Р ₁ Сурет 2- Жер эллипсоиды

Р ₁ QРQ ₁ эллипстің РР ₁ кіші осінің төңірегінде айналуынан пайда болған бетті жер эллипсоидының беті немесе сфероид деп атайды ( сурет 2 ) . Жер эллипсоидының көлемі оның жарты осьтерінің ұзындықтары a (үлкен жарты осі), b (кіші жарты осі) және Жердің полярлық сығылуы немесе сфероидтың қысыңқылығы арқылы сипатталады.

α = (a - b)

Жер фигурасын зерттеу үшін геоидқа шамалас келетін жерге дұрыс бағытталған эллипсоидтың жарты осьтерінің және оның полярлық сығылу шамаларын анықтау.

Ондай эллипсоидты референц-эллипсоид деп атайды. Оның a, b шамаларын меридианның 1 ⁰ -тағы доғасы ұзындығын есептеу арқылы табады. Әр жерде меридиандардың доғаларының ұзындықтарын білу арқылы Жердің пішіні мен көлемін анықтауға болады.

Жер эллипсоидының мөлшерін әр елдің ғалымдары бірнеше рет анықтады. Бұрынғы Одақта 1841 жылы неміс ғалымы Ф. В. Бессель есептеп шығарған жер эллипсоидының көлемі қолданылды

(а=6377397 м, b=6356079 м, α═(а-в) /а=1:299, 2) .

Жер эллипсоидының мөлшерін үлкен дәлдікпен 1940 жылы Ф. Н. Красовский мен А. А. Изотовтың басқаруымен Совет ғалымдары біздің территорияда есептеп анықтады. Оның үлкен жарты осі а=6378245 м, кіші жарты осі b=6356863 м және сфероидтың қысыңқылығы α═(а-в) /а=1:298, 3 . Оны Ф. Н. Красовскийдің құрметіне Красовский эллипсоиды деп атады. Ғарыштық геодезия әдістерімен алынған нәтижелері Красовскийдің есептеулерінің дұрыс екенін, әсіресе жердің полярлық сығылу коэффициенті мәнінің дұрыстығын дәлелдеді. Жердің пішіні туралы қазіргі теориялар ғылым академиясының корреспондент мүшесі М. С. Молоденскийдің жұмыстарында дамуда. Кейбір елдерде геодезиялық өлшеулер нәтижесінде шығарылған өз эллипсоидтарын қолданады. Олар сол немесе бірнеше елдің аумағын толық не ішінара қамтиды. Мұндай эллипсоид - референц-эллипсоид деп аталады. Референц-эллипсоид дегеніміз нақты бір елде геодезиялық өлшеулерді өңдеу үшін қолданылатын, жер денесінде белгілі түрде бағдарланған, нақты көлемі анықталған эллипсоид.

Сөйтіп, қазіргі кезде Красовскийдің референц-эллипсоиды Ресейде ғана емес, бүкіл ТМД және Батыс Еуропа мен АҚШ-тың гравиметриялық және астрономиялық өлшеулері нәтижесінде алынған жер эллипсоидының көлемі - басқа елдердегі анықтамаларға қарағанда, қолданылған материалдардың аумағы жағынан да, оларды өңдеудің дәлдігі жағынан да неғұрлым басым.

1960 жылы Жердің үш жасанды серіктерін бақылаудың нәтижесінде жер сфероидының қысыңқылығы α=1:298, 2 -ге тең, ал АҚШ-та ұшырылған Жердің 13 жасанды серіктерін бақылау арқылы (1962 жылы ) α=1:298, 31 -ге тең екендігінің анықтаулары Красовский өлшеулерінің дүниежүзілік маңызы бар екендігінің айқын дәлелі.

Жердің сығылу коэффициенті аз болғандықтан (α=1:300) көп есептерді шешкенде Жердің пішіні ретінде тәжірибелік мақсаттағы дәлдікпен шамасы жер эллипсоидының көлеміне тең сфераны алуға болады. Жер бетінің шағын учаскелерінде геодезиялық жұмыстармен қатар, көптеген инженерлік есептерді шығаруда эллипсоид сығылушылығының аз болғандығынан, жердің пішіні үшін шарды радиусы R=6371, 11 км қолдануға да болады.

Жердің физикалық беті әртүрлі кеңістік пішіндердің жиынтығынан тұрады (тау, ой, сай, жота және т. б. ) .

Жер бетіндегі нүктелердің жазықтықтағы жайын анықтау үшін геодезияда проекция әдісі қолданылады. Жердің кеңістік пішіндерін қағазға бейнелеу геодезияда ортогональдық (тік бұрышты) проекциямен көрсетіледі.

Биіктіктің шамасы деңгей беттен басталып саналса, ондай биіктікті абсолюттік биіктік деп атайды. Ал егер биіктіктің шамасы деңгей бетке параллель кез-келген беттен саналатын болса, ондай биіктікті шартты (салыстырмалы) биіктік дейді.

Әдетте, абсолюттік биіктікті санау мұхит немесе теңіздің тыныш күйіндегі деңгейінен бастайды. Елімізде абсолюттік биіктік санағы Кронштад футштогының нолінен басталады. Футшток деген мыстан жасалған, көлденең сызықтың тұсына ноль саны көрсетілген тақта. Осы бөліктер бойынша жиі-жиі теңіз деңгейі есептеліп отырылады. Ол Балтық теңізінің орта деңгейінен алынады, сондықтан біздің елдегі биіктік жүйе Балтық жүйесі деп аталады.

Биіктіктің санмен өрнектелген шамасын нүктенің биіктік мәні (абсолюттік, шартты) дейді ( сурет 3 ) .

Екі нүктенің биіктік мәнінің (абсолюттік немесе шартты) айырымын нүктелердің өзара биіктігі (биіктік өсімшесі) деп атайды, яғни айтқанда:

h=H _В -H _А

Шартты биіктіктен абсолюттік биіктікке көшкенде немесе керісінше болғанда шартты деңгеймен басты деңгейлі беттің арасындағы ұзындықты білу қажет.

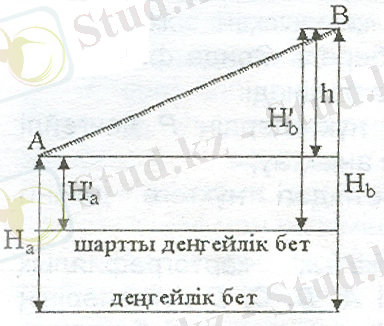$C:\Users\балдаурен\Desktop\Дидар Универ\Без названия (2).png$ Сурет 3

ЖЕР ПІШІНІН ЗЕРТТЕУ ӘДІСТЕРІ

Гравиметриялық әдіс: Гравиметрияда Жердің гравитациялық өрісін әдетте екі негізгі күштің нәтижесі болып табылатын ауырлық өрісі (немесе санның тең тартылыс үдеуі) анықтайды: Жердің тартылу күші (центрден тепкіш күш) оның күнделікті айналуына байланысты. Айналу осінен алысқа бағытталған центрифугалық күш ауырлық күшін азайтады, ал экваторда. Полюстерден экваторға қарай тартылыс күшінің төмендеуі де Жердің қысылуына байланысты.

Ауырлық күші, яғни Жердің (немесе басқа планетаның) маңындағы бірлік массаға әсер ететін күш ауырлық күштері мен инерция күштерінен (центрден тепкіш күш) тұрады:

мұндағы G - гравитациялық тұрақты, mu - массалық бірлік, dm - массалық элемент, R - өлшеу нүктесінің радиус векторлары, r - массалық элементтің радиус векторы, w - Жердің айналу бұрыштық жылдамдығы; интеграл барлық массаға қабылданады.

Гравитация потенциалы сәйкесінше мына қатынаспен анықталады:

мұнда - өлшеу нүктесінің ені

Гравиметрияның негізгі мазмұны - жер бетіндегі өлшеулер мен астрономиялық -геодезиялық мәліметтерден Жердің сыртқы потенциалы мен гравитациясын анықтаудың теориясы мен әдістері, планеталардың ішкі құрылысын зерттеу және кейбір навигациялық есептерді шешу.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.