ИРРАЦИОНАЛ ТЕҢДЕУЛЕРДІ ШЕШУДЕ ТРИГОНОМЕТРИЯЛЫҚ АЛМАСТЫРУЛАРДЫ ҚОЛДАНУ

Жұмыс түрі: Іс-тәжірибеден есеп беру
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі

Түркістан облысының адами әлеуетті дамыту басқармасы

Н.Оңдасынов атындағы Түркістан мамандандырылған мектеп-интернаты

Әбдіқадырқызы Гүлайша
10 сынып оқушысы

ИРРАЦИОНАЛ ТЕҢДЕУЛЕРДІ ТРИГОНОМЕТРИЯЛЫҚ ТҮРЛЕНДІРУЛЕР КӨМЕГІМЕН ШЕШУ

Секциясы:
Математика

Ғылыми жетекші:
Математика пәнінің мұғалімі Момбеков Азамат Ыдырысұлы

Ғылыми кеңесші:
Қ.А.Ясауи атындағы ХҚТУ
аға оқытушысы,PhD докторы
Сәрсенов Бақытбек Темирбекович

Түркістан, 2020

Айқындама

Бұл ғылыми жұмыс иррационал теңдеулерді тригонометриялық алмастырулар көмегімен шешуге негізделген.Осы теорияның негізінде иррационал теңдеулерді шешудің негізгі әдістері қарастырылған, ал түрлендірілген теңдеудің шешімдері берілген теңдеудің шешімдері болу-болмау мәселесін теңдеудің мүмкін мәндер облысына тиісті болуына не тиісті болмауын анықтаумен анықталған. Сонымен қатар, сыртқы бейнесінде мүлдем ұқсастығы жоқ иррационал теңдеулер мен тригонометриялық функцияларды байланыстырып, иррационал теңдеулерді шешуді мектеп бағдарламасында қолданысқа енгізу қарастырылды .
Осы әдіс емтихандарда,олимпиадаларда күрделі есептерді шешуде психологиялық кедергілерді жеңуге көп мүмкіндік береді.

Аннотация

Эта работа основана на решении иррациональных уравнений с помощью тригонометрической замены, на основе этой теории рассматриваются основные методы решения иррациональных уравнений, а решения модифицированного уравнения определяются тем, является ли решение данного уравнения подходящим или нет. В то же время рассматривается вопрос о введении в школьную программу иррациональных уравнений, включающих нерелевантные уравнения и тригонометрические функции, не имеющие аналогов во внешнем изображении.
Этот метод дает много возможностей для преодоления психологических барьеров на экзаменах, соревнованиях на Олимпиаде.

Annotation

This work is based on the solution of irrational equations using a trigonometric replacement, on the basis of this theory the basic methods for solving irrational equations are considered, and the solutions of a modified equation are determined by whether the solution to this equation is suitable or not. At the same time, the question of introducing irrational equations into the school curriculum, including irrelevant equations and trigonometric functions that have no analogues in the external image, is being considered.
This method provides many opportunities to overcome psychological barriers in exams and competitions at the Olympics.

МАЗМҰНЫ

КІРІСПЕ
3

1
ИРРАЦИОНАЛ ТЕҢДЕУЛЕРДІ ШЕШУДІҢ ТӘСІЛДЕРІ
5
1.1
Иррационал теңдеулерді шешудің қарапайым тәсілдері
5
1.2
Иррационал теңдеулерді шешудегі тригонометриялық алмастырулар

7

2
ИРРАЦИОНАЛ ТЕҢДЕУЛЕРДІ ШЕШУДЕ ТРИГОНОМЕТРИЯЛЫҚ АЛМАСТЫРУЛАРДЫ ҚОЛДАНУ

9
2.1
Иррационал теңдеулерді тригонометриялық түрлендірулер көмегімен шешу

9
2.2
Параметр арқылы берілген иррационал теңдеулерді шешу
21
2.3
Тригонометриялық түрлендірулер арқылы теңдеулер жүйесін шешу

24

ҚОРЫТЫНДЫ
29

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

30

КІРІСПЕ

Бұл ғылыми жұмыс жалпы білім беретін мектеп оқушыларының стандартты емес есептерді шешу мүмкіндігін жетілдіруде өзіндік ерекшеліктері бар. Атап айтсақ, мектеп бағдарламасына енетін материалдар мен математиканы тереңдетіп оқытатын мектеп бағдарламасында мүлдем қарастырылмайтын иррационал теңдеулерді тригонометриялық түрлендірулермен шешуге арналған практикалық есептер қарастырылған.
Оқу қызметінің маңызды бір түрі есеп шығару болып табылады. Есеп шығару процессінде оқушы математикалық теориямен танысады және логикалық ойлау мен шығармашылық қабілеттері дамиды. Математика пәнінде жоғары сынып оқушыларының шығармашылық қабілеттерін дамыту үшін ең тиімді тәсіл,оқыту кезіңінде қатысушыларды шығармашылық қызметке тарту болып табылады.
Математикадан күрделі есептерді шешу көп жағдайда оларды шешу тәжірибесіне, оларды шешу әдістерімен қайта құру техникасын меңгеру дәрежесіне байланысты. Стандартты емес есеп деп, есепті шығаруда дайын алгоритмі жоқ және негізгі идеяны өз бетінше іздеуді талап ететін есептерді айтамыз. Стандартты емес есептерді шешу кезінде математикалық мәдениет қалыптасады,ақыл-ойдың икемділігі тәрбиеленеді және математика бірлігін қалыптастыру жүзеге асырылады.
Олимпиада және конкурстық тапсырмалар стандартты емес тапсырмалардың маңызды бөлігі болып табылады.Әдетте, стандартты емес есептерді шығару үшін стандартты емес көзқарасты талап етіледі.Ең маңыздысы, оқушылар стандартты емес тапсырмаларды шешу әдістерінің жинағын құрып алу қажет, өйткені оқушылар стандартты емес есеп шығару әдісітерін өз бетінше ойлап таба алмайды.
Біріншіден, алгебралық есептерді шешудің стандартты мектеп тәсілдері қөзқарасынан, тригонометриялық алмастыру әдісі стандартты емес әдіс болып табылады.
Екіншіден, тригонометриялық алмастыру күрделі есептерді шешуге мүмкіндік береді. Ол өз құралдарымен шешілмейтін немесе өте қиын шешілетін алгебралық есептерді шешу кезінде қолданылады.
Математиканы тереңдетіп оқытатын сынып оқушылары тригонометриялық алмастыру әдісімен танысады, оны терең және толық зерделеудің мәні бар.
Жұмыс мақсаты: математиканы тереңдетіп оқытатын сыныптарда олимпиада және конкурстық тапсырмаларды шешуде мектеп оқушыларының қолданысына енгізу.
Зерттеу объектісі:әртүрлі иррационал теңдеулерді шешу әдісі ретінде тригонометриялық алмастыруды қолдану процесі.
Зерттеу нысаны:математиканы тереңдетіп оқытатын сыныптарда факультативтік сабақтарда тригонометриялық алмастыруды меңгеру бойынша оқушылардың қызметін ұйымдастыру.
Гипотеза:Зерттеу барысында көптеген есептерді шешудің салыстырмалы талдауы негізінде әзірленген практикалық есептердің қолданылуы, оқушылардың шығармашылық қабілеттерін дамытуға мүмкіндік береді және оларды жоғары оқу орындарына түсу емтихандарына дайындайды.
Қойылған мақсатқа жету және гипотезаны тексеру үшін келесі міндеттерді шешу қажет:
1. Тригонометриялық алмастыруды енгізу мүмкіндігінің теориялық негіздерін анықтау.
2. Тригонометриялық алмастыр арқылы және тригонометриялық алмастырусыз есептерді шешудің салыстырмалы талдауын жүргізу.
3. Жүргізілген салыстырмалы талдау негізінде математиканы тереңдетіп оқытатын жоғары сыныптардағы математика пәнінен факультативтік сабақтарда иррационал теңдеулерді шешу кезінде тригонометриялық алмастыруды зерттеу практикалық есептерін әзірлеу. Ғылыми жұмыстың құрылымы: ғылыми жұмыс кіріспеден, екі тараудан, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.

1.ИРРАЦИОНАЛ ТЕҢДЕУЛЕРДІ ШЕШУДІҢ ТӘСІЛДЕРІ

1.1Иррационал теңдеулерді шешудің қарапайым тәсілдері

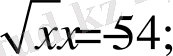
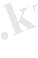
Түбір таңбасы астында айнымалылары бар теңдеулерді иррационал теңдеулер деп атаймыз. Мысалы тағы сол сияқты иррационал теңдеулер болады. Ал иррационал теңдеу болмайды, өйткені түбір таңбасы астында айнымалы жоқ.
Иррационал теңдеулердегі түбірлер арифметикалық түбірлер ретінде қарастырылады. Сондықтан түбірдің мәнін теріс емес деп есептейміз. Мысалы, 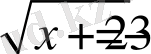иррационал теңдеуінің шешімі болмайды, өйткені 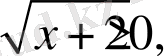ал 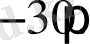Әдетте, иррационал теңдеулерді шешу үшін оларды түрлендіріп, рационал теңдеуге келтіріп алады. Енді иррационал теңдеулерді шешуге бірнеше мысалдар қарастырайық.

1-есеп. 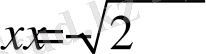теңдеуінің түбірлерін табу керек.
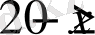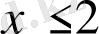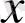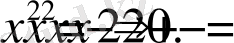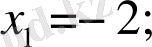
Шешуі: Бұл теңдеудің анықталу облысы ,не теңсіздігімен анықталады. Осы теңсіздікті қанағаттандыратын -тердің ішінен берілген теңдеудің табу керек. Ол үшін теңдеудің екі жақ бөлігін квадраттаймыз: Бұл теңдеудің түбірлері 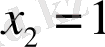. Бұл түбірлерді теңдеудің анықталу облысында жатады. Бірақ бұл сандарды берілген теңдеудің түбірлері ретінде қабылдауға болмайды. Себебі 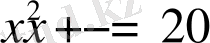теңдеуіне 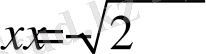теңдеуін квадраттау нәтижесінде келдік. Екінші жағынан 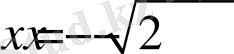теңдеуін де квадраттау нәтижесінде 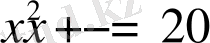теңдеуін алуға болады. Осылай болса, берілген теңдеудің квадраттау барысында біздер бөгде түбірлер қосып алуымыз мүмкін. Табылған шешімдердің арасында бөгде түбірлер бар немесе жоқтығын анықтаудың екі түрлі тәсілі бар.
Біріншісі-тексеру тәсілі. Мұнда табылған шешімдердің берілген теңдеулерді қанағаттандыратындығын тексереді.
Тексеру. Егер 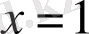болса, онда теңбе-теңдігін аламыз, яғни 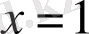берілген теңдеудің түбірі бола алады. Ал 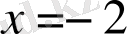болса, 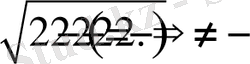Олай болса 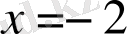, бөгде түбір. Сонымен есептің жауабы .
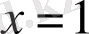Екіншісі М.М.Ж мүмкін мәндер жиынын анықтау тәсілі. Теңдеудің М.М.Ж 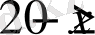және
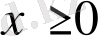
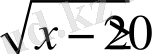( болғандықтан) теңсіздіктер жүйесімен анықталады. Осыдан М.М.Ж қос теңсіздігімен анықталатындығы шығады. Енді 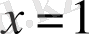және 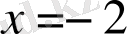шешімдерінің ішінен берілген теңдеудің М.М.Ж-на енетінін белгілеп, оның түбірін анықтаймыз. [1]
Жауабы:

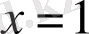
2-есеп. 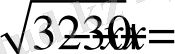теңдеуін шешіңіз.
Шешуі:түрінде жазып, оның М.М.Ж-ын 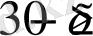және 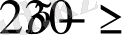теңсіздіктері жүйесімен анықтаймыз. Онда М.М.Ж 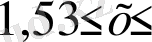теңсіздігі немесе 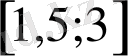жиынымен анықталады. Енді теңдеуін квадраттап 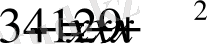немесе 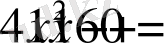теңдеуін аламыз. Оның түбірлері 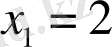және 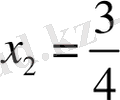. Бұл түбірлердің біріншісі ММЖ-на енсе, екіншісі енбейді. Ондай терілген теңдеудің жалғыз 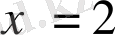түбірі болады.
Жауабы:

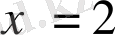
3-есеп.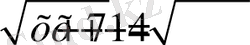теңдеуін шешу керек.
Шешуі: М.М.Ж 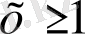теңсіздігіме анықталады. Енді берілген теңдеуді 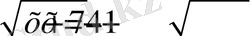түрінде жазып, оның екі жақ бөлігін де квадраттаймыз: . Соңғы теңдеуді тағы да квадраттап, 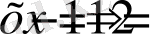теңдігін аламыз. 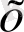-тің бұл табылған мәні берілген теңдеуді қанағаттандырады.
Жауабы:
4-есеп. 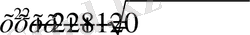теңдеуінің түбірлерін табу керек.
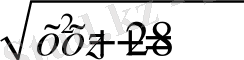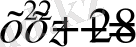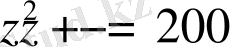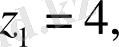
Шешуі: ,белгілеуін енгізсек, онда . Сонда берілген теңдеуді түрінде жазып, оның түбірлерін анықтаймыз: 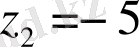.Онда еңгізген белгілеуді еcкере отырып, 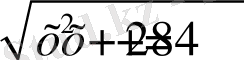теңдеуін аламыз
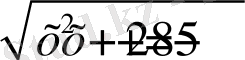( теңдігінің мағынасы жоқ). Бұл теңдеуді квадраттағанда 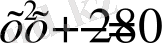квадрат үшмүшесі шығады. Оның түбірлері: 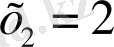. Енді табылған түбірлердің берілген теңдеуді қанағаттандыратынын тексеру керек. Тексеру:
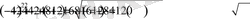және
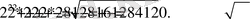
Яғни табылған екі түбір де берілген теңдеуді қанағаттандырады.[2]
Жауабы: .
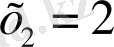5-есеп. 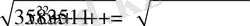(1) теңдеуін шешейік.
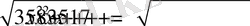Шешуі: (1) теңдеудің екі бөлігін де өрнегіне көбейтсек, теңдеуін аламыз. (2)
(1) және (2) теңдеулерді мүшелеп қосып, немесе теңдеуін
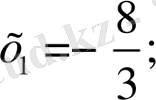
аламыз. Оның түбірлері: . Тексеру: болса, болса, онда
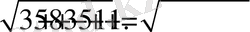
Жауабы:

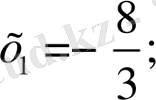
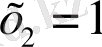
1.2 Иррационал теңдеулерді шешудегі тригонометриялық
алмастырулар

Тригонометриялық алмастыру айнымалыны ауыстыру әдісін іске асыру тәсілдерінің бірі болып табылады және бастапқы теңдеуді анықтау саласы тригонометриялық функцияның мәнінің аясына сәйкес келген немесе осы салаға қосылатын жағдайларда пайдаланылады. Қандайда бір функцияны таңдау теңдеудің түріне немесе алгебралық өрнектеріне байланысты.
1.Егер берілген есептегі радикал 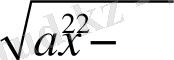түрінде болса, онда алмастыруын енгіземіз, мұндағы 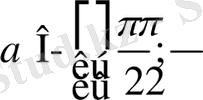. Сонымен қатар алмастыруын енгізуге болады. Сол кезде немесе алмастыруын аламыз.
Егер есеп шарттарынан айнымалының рұқсат етілген мәндері 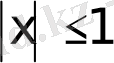теңсіздігімен анықталса, онда немесе ауыстыруы ыңғайлы.
Бірінші жағдайда 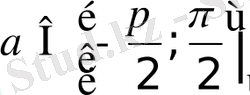қарастыру жеткілікті, бұл аралықта үздіксіз функциясы өседі, сондықтан әрбір өз мәнін бір нүктеде дәл қабылдайды.
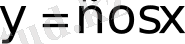үздіксіз функциясы 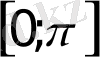аралықта азайады, сондықтан, сондай-ақ, әрбір өз мәнін дәл бір нүктеде қабылдайды.
Сондықтан ,ауыстыру кезінде, алу жеткілікті. Екі тәсілдің қайсысын таңдау, нақты жағдайға байланысты.

2.Егер берілген есептегі радикал 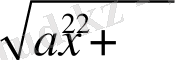түрінде болса, онда 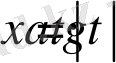алмастыруын енгіземіз, мұндағы 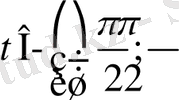немесе 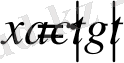,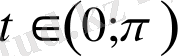Сонымен қатар 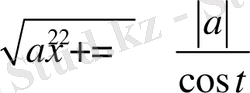немесе 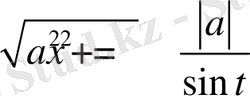алмастыруларын енгіземіз.
Айнымалы кез келген нақты мәндерді қабылдай алатын жағдайларда,немесеауыстыруы қолданылады, өйткені және функциясының мәнінің аймағына сәйкес аралықтарда барлық нақты сандардың жиыны бар.

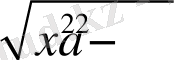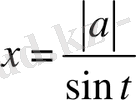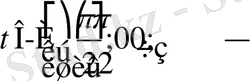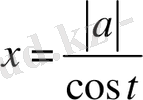
3. Егер шартты есепте радикал түрінде болса, онда алмастыруын енгіземіз, мұндағы немесе 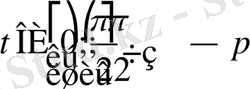[3]
Мұндай алмастыруларды жүзеге асыру аса қиын емес, бірақ қалай алмастыру тиімді екенін көре білу қажетті.Сондықтан тригонометриялық алмастыруларды таңдап, үйренуге кеңес береміз.Келесі тарау тиісті дағдыларды дамытуға тікелей бағытталады.

.

2. ИРРАЦИОНАЛ ТЕҢДЕУЛЕРДІ ШЕШУДЕ ТРИГОНОМЕТРИЯЛЫҚ АЛМАСТЫРУЛАРДЫ ҚОЛДАНУ
2.1 Иррационал теңдеулерді тригонометриялық түрлендірулер
көмегімен шешу

Иррационалды теңдеулер математикадан жоғары оқу орындарына түсу емтихандарында жиі кездеседі, олардың көмегімен тепе-теңтүрлендірулер, анықтау саласы және басқалар сияқты ұғымдарды білу оңай диагностикаланады. Иррационалдық теңдеулерді шешу әдістері, әдетте, иррационалдық теңдеуді рационалды теңдеумен ұтымды етіп ауыстыру мүмкіндігіне негізделген.Жиі теңдеудің екі бөлігі де бірдей дәрежеге көбейеді. Екі бөлікті тақ дәрежеге көбейту кезінде эквиваленттілік бұзылмайды.Олай болмаған жағдайда табылған шешімдерді тексеру немесе теңдеудің екі бөлігінің белгісін бағалау талап етіледі. Бірақ иррационалды теңдеулерді шешу кезінде тиімді басқа әдістер бар. Мысалы, тригонометриялық алмастыру әдісі.
Сыртқы көрінісінен тригонометрияға еш қатысы жоқ иррационал теңдеуді қарастырып, шешу тәсілін көрсетейік.

6-есеп. Теңдеуді шешіңіз:

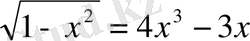
Иррационал теңдеудің сол жақ бөлігіндегі квадрат түбір астындағы өрнек
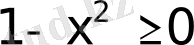болуы қажетті. Квадрат теңсіздікті көбейткіштерге жіктеп, интервалдар әдісімен шешеміз.
+
-
-
- 1
1

аралығында теңдеудің мағынасы бар.
Сондықтан 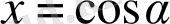алмастыруын енгізейік, мұндағы .
Бұл жағдайда теңдеу мына түрге енеді:

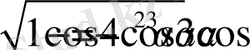
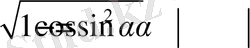екенін байқау қиын емес. аралығына тиістілігін ескере отырып теңдігін аламыз.

Теңдеудің сол жақ бөлігіне косинустың үш еселенген бұрыш формуласын қолданайық сонда,

Келтіру формуласы арқылы синусты косинус арқылы өрнектейік.

Тригонометриялық функциялардың айырмасын көбейтіндіге айналдыру формуласы
қолданайық.
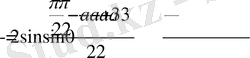
Сонда, 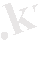теңдігін аламыз.

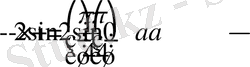
Алынған көбейтіндінің мәні нөлге тең болады,егер көбейтіндігің кем дегенде біреуі нөлге тең болса.

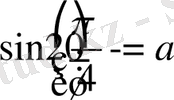және

,
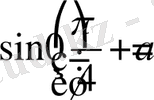
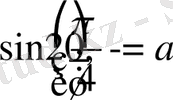
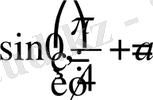
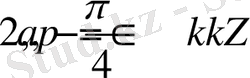
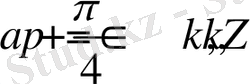
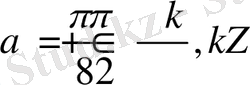
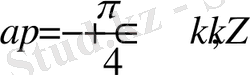
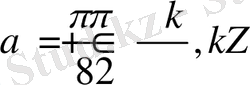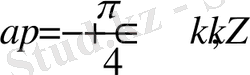
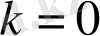болса, онда
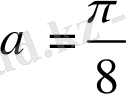
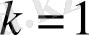болса, онда
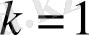болса, онда
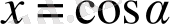алмастыруынан ті табайық ол үшін жарты бұрыш формулалары 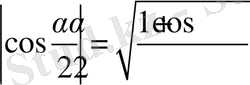, 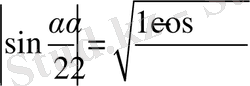қолданайық.
Сонда,

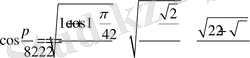
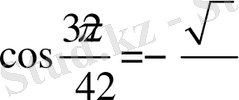мәндерін аламыз.
Жауабы:

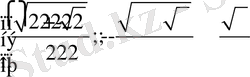
Алгебралық әдіс
Салыстыру үшін осы теңдеуді алгебралық тәсілмен шешіп көрсетейік.Ол үшін теңдеудің екі жағын да квадраттаймыз. Теңдеудің сол жағындағы өрнек нөлден үлкен немесе тең.

теңдеуі үшін алмастыруын енгізейік.Сонда, теңдеу

түріне енеді. Бұл теңдеудің түріндегі бөлшек түбірлерін іздейік.Мұндағы бос мүше бөлгіштері ,
мәні теңдеудің түбірі бола ма? Деген сұраққа Горнер схемасы арқылы жауап беріп көрейік.

16
-24
10
-1
12
16
-16
2
0
Осылайша , көпмүлелігіне жіктелуін аламыз.
Квадрат үшмүшенің өзін нөлге теңестіріп түбірлерін табайық.

,

Кері алмастыру жасайық
онда
онда

онда

Теңдеуді шешу барысында алты әртүрлі түбірлер табылды.Осы табылған түбірлер ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.