Дұрыс көпжақтар: тарихы, ұғымы, қасиеттері және практикалық қолданылуы


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
М. Х. ДУЛАТИ АТЫНДАҒЫ ТАРАЗ ӨҢІРЛІК УНИВЕРСИТЕТІ
«ҰСТАЗ» ИНСТИТУТЫ
Кафедра «Математика»
КУРСТЫҚ ЖҰМЫС
Тақырыбы: «Дұрыс көпжақтар»
Тобы: М-18-1(к)
Курс: III
Қабылдаған: Жумалиева Л. Д
Орындаған: Ералы А. Н
Тараз - 2020ж
МAЗМҰНЫ
КІРІСПЕ . . . 3
НЕГІЗГІ БӨЛІМ . . . 5
1. ДҰРЫС КӨПЖАҚТАР ТУРАЛЫ ТАРИХИ МӘЛІМЕТТЕР . . . 5
2. ДҰРЫС КӨПЖAҚТAРДЫҢ ҰҒЫМЫ, ТҮРЛЕРІ, ҚAСИЕТТЕРІ . . . 7
3. ДҰРЫС КӨПЖAҚТAРДЫ ПРAКТИКA ЖҮЗІНДЕ ҚОЛДAНУ . . . 14
4. ДҰРЫС КӨПЖAҚТAР БІЗДІҢ AЙНAЛAМЫЗДA . . . 19
ҚОРЫТЫНДЫ . . . 20
ПAЙДAЛAНЫЛҒAН ӘДЕБИЕТТЕР . . . 21
КІРІСПЕ
«Дұрыс көпжақтар өте аз, бірақ бұл өте қарапайым отряд әртүрлі ғылымдардың тереңдігіне ене алды» -Льюис Кэрролл.
Біз өмір сүріп жатқан әлемде өте ерекше және керемет дүниелер өте көп. Бізді заттар, әлі күнге дейін таң қалдыратын түрлі пішіндер қоршап тұр. Мысалға алып қарасақ, осындай керемет дүниелердің бірі дұрыс көпжақтар. Бұл фигуралар сұлулыққа, пішіндердің тартымдылығына ие.
Ойланып қарасақ біз бала кезден бастап айналамызда дұрыс көпжақтарды көп кездестіреміз. Мысалға есімізге түсірейікші, ерте жаста ойнаған «кубиктер» әлемге танымал ойынының мәні көпжақтардан бір объект салу ед. Кубик-рубик текшелерінің жұмбақтарын шешіп, дұрыс көпжақтармен таныстық.
Сәулетшілер, құрылысшылар және дизайнерлер осы фигураларды қолдана отырып, өзіңдік идеяларын жүзеге асырады.
Біздің әлем симметрияға толы. Ежелгі дәуірден бастап біздің сұлулық идеяларымыз онымен байланысты. Бұл Платон мен Евклидтен бастап, Эйлер мен Кошиге дейінгі көптеген көрнекті ойшылдардың назарын аударған симметрияның таңғажайып символдары - адамның дұрыс көпжақтарға деген қызығушылығын түсіндіруі мүмкін.
Байқап қарасақ адам өзінің саналы іс-әрекет өмірінің барлығында дұрыс көпжақтарға қызығушылық танытады. Тарихта дұрыс көпжақтарды зерттеу, оларды одан әрі қолдану тұрғысынан ғана емес, сонымен бірге ғаламның құрылымы мен кеңістіктің табиғаты туралы философиялық мәселелерді түсіну мақсатында жүргізілді.
Қазіргі таңда дұрыс көпжақтар ғылым мен техниканың көптеген салаларында қолданылады. Қазіргі замаңғы ғимараттар, радиоқабылдағыштар, теледидарлар, сіріңке қорабы, кітап, бөлме, т. б. заттар тетраэдр формасы түрінде болады. Ешқандай геометриялық денелер дұрыс көпжақтар сияқты сұлулыққа, ғажайыптылыққа ие емес.
«Тек геометрия заңдарына сүйене отырып, ежелгі сәулетшілер өздерінің туындыларын жасай алды. Хеопс пирамидасы - геометрия туралы үнсіз трактат, ал грек архитектурасы - Евклид геометриясының сыртқы көрінісі деп айту кездейсоқтық емес. Ғасырлар өтті, бірақ геометрияның рөлі өзгерген жоқ. Ол әлі де сәулетшінің грамматикасы болып табылады» - бұл сөз біздің жүз жылдық ғасырдың француз архитекторы Ле Корбюзьеге тиесілі.
Осы курстық жұмыста біз дұрыс көпжақтар туралы тарихи мәліметтер, олардың түрлерімен, қасиеттерімен, табиғатта кездесуімен танысатын боламыз және практикалық тұрғыда есептер шығарамыз.
- Қандай көпжақтар «Дұрыс көпжақтар» деп аталады?
- Олардың қасиеттері қандай?
- Олар табиғатта қай жерде кездеседі және іссжүзінде қайда қолданылады?
Осындай, және басқада сұрақтарға жауап іздейтін боламыз.
ДҰРЫС КӨПЖАҚТАР ТУРАЛЫ ТАРИХИ МӘЛІМЕТТЕР
Дұрыс көпжақтардың тарихы ежелгі дәуірден басталады. Пифагор мен оның шәкірттері дұрыс көпжақтарды зерттеумен айналысты. Пифагор шәкірттерін осы фигуралардың сұлулығы, үйлесімділігі, дәлдігі таң қалдырды. Пифагорлықтар дұрыс көпжақтарды өте керемет фигуралар деп атап, оны өздерінің философиялық еңбектерінде қолданды. Кейінірек пифагорлықтардың дұрыс көпжақтар туралы ілімдерін ежелгі грек ғалымы, идеалист, философ Платон өз трактатында (Тимей) сипаттаған. Осыдан кейін дұрыс көпжақтарды халық «Платон денелері» деп атап кеткен.
Дұрыс көпжақтардың моделі Платоннан кем дегенде 1000 жыл бұрын Шотландияда кеш неолит заманында ою-өрнектелген тастардан кездестіруге болады. Негізінде дұрыс көпжақтар ежелгі гректер зерттеген. Кейбір дереккөздерде (Мысалы, Прокл Диадох) дұрыс көпжақтардың зерттелуін Пифагорға жатқызады. Басқаралы оған тет тетраэдр, куб және додекаэдр таныс болған деп болжайды, ал октаэдр мен икасаэдрді ашу құрметі Платонның замандасы Афиналық Теэттетке тиесілі. Қалай болса да, Теэтет барлық бес дұрыс көпжақтарға математикалық сипаттама берді және олардың дәл бесеу екендігі туралы алғашқы дәлелін негіздеген.
Евклид соңғы, XIII кітапта (Начал-Бастау) дұрыс көпжақтардың толық математикалық сипаттамасын берді. Осы кітаптың 13-17 сөйлемдерінде тетраэдр, октаэдр, куб, икасаэдр және додекаэдр құрылымдары сипатталады. Әрбір сипатталған дұрыс көпжақтар үшін Евклид сферада диаметрдің қабырға ұзындығына қатынасын тапты. Ең қызығы 18 сөйлемде Евклид басқа дұрыс көпжақтың жоқ екендігін айтады.
XVI ғасырда неміс астрономы Иоганн Кеплер сол кезде белгілі болған Күн жүйесінің бес планеталары (жерді есептемегенде) мен дұрыс көпжақтар арасында байланыс табуға тырысты. 1596 жылы Иоганн Кеплердің жарық көрген «Әлемнің Құпиясы» атты кітабында Күн жүйесінің моделін ұсынған болатын. Ол кітапта бес дұрыс көпжақтар бірінен кейін бірі бөлініп әр сферада орналастырылған. Әр сфера бір планетаға сай келген (Меркурий, Шолпан, Жер, Марс, Юпитер және Сатурн) . Кеплердің космологиялық гипотезасы өте ерекше, онда ол Күн жүйесінің кейбір қасиеттерін дұрыс көпжақтардың қасиеттерімен байланыстыруға тырысты. Дұрыс көпжақтар келесі ретпен орналастырылған (іштен сыртқа) : октаэдр, одан кейін икасаэдр, додекаэдр, тетраэдр, және әрине одан кейін гексаэдр (куб. Осылайша Күн жүйесінің құрылымы мен планеталар арасындағы қашықтық қатынасы дұрыс көпжақтармен анықталды. Кейінірек Кеплердің бастапқы идеясынан бас тартуына тура келеді, бірақ оның ізденістерінің нәтижесі физика мен астрономия бағытын өзгерткен орбиталық динамика заңдарының, сондай -ақ жұлдыз тәрізді дұрыс көпжақтардың ашылуы болды (Кеплер-Пуансо денелері) .
Қызығы аралар адам пайда болғанға дейін алты қырлы ұялар салған, ал өркениет тарихында пластикалық өнердің басқа түрлерімен бірге көп қырлы денелерді (пирамидалар) жасау ғасырлар бойы жалғасуда.
Мыңдаған жылдар бойына тамыр жайған көпжақтарды зерттеу және бейнелеу тарихы осы күндері жалғасуда, күтпеген жерден фуллерен ғылымы мен оларға негізделген жаңа материалдар технологиясы қазіргі сәулет өнерінің тарихына айналды.
ДҰРЫС КӨПЖAҚТAРДЫҢ ҰҒЫМЫ, ТҮРЛЕРІ, ҚAСИЕТТЕРІ
Көпжақ , үш өлшемді кеңістікте - бірнеше (шектеулі) жазық көпбұрыштан құрылған геометриялық бет.
Егер дөңес көпжақтың жақтары қабырғаларының саны бірдей дұрыс көпжақтар болса және көпжақтың әрбір төбесінен шығатын қырларының саны бірдей болса, онда оны дұрыс көпжақ деп атайды. Бар болғаны бес дұрыс көпжақ бар. Олар:
- Тетраэдр (грек сөзі «тетра» - төрт және «едра» - жақ) ;
- Гексаэдр (куб) («гекса» - алты) ;
- Октаэдр («окто» - сегіз) ;
- Додекаэдр («додека» - он екі) ;
- Икосаэдр («эйкоси» - жиырма) ;
Дұрыс көпжақтардың қасиеттері туралы ең алғаш рет грек ғалымы Платон тапты. Сондықтан дұрыс көпжақтар “ Платон денелері” деп аталады. Платон тіршілік негізін құраушы су, ауа, жер, оттан тұрады деп есептеді. Осы заттардың атомдарының формасы дұрыс көпжақтарға ұқсайды(Б. э. д428-348) .
Платон философиялық тұрғыда тетраэдр -от, себебі төбесі жоғарыға ұмтылған жанып тұрған отқа, ал икосаэдр -су; гексаэдр (куб) -өте орнықты фигура - жерге, октаэдрды -ауаға, додекаэдрды - күнге теңеген.
Егер дөңес көпжактың барлық жақтары тең дұрыс көпбұрыштар болса, сонымен қатар оның әрбір төбесінде саны бірдей қырлар тоғысатын болса, ондай дөңес көпжақ дұрыс көпжақ деп аталады. Мысалы, куб дұрыс көпжак болып табылады. Оның барлық жақтары тең квадраттар жөне әр төбесінде үш қыр тоғысады.
Дұрыс көпжақтың барлық қырлары бір-біріне тең екені көрініп тұр. Қыры ортақ екі жақты қамтитын барлық екіжақты бұрыштар да тең екенін дөлелдеуге болады. Шынында да, n-бұрыштың n≥6 болғанда бұрышы 120 0 -тан кіші болмайды.
Екінші жағынан, көпжақтың әрбір төбесінде үштен кем жазық бұрыш болмауы тиіс. Сондықтан, егер жақтары n≥6 болғанда дүрыс n-бұрыш болатын дұрыс көпжақ бар болса, онда мұндай көпжақтың әрбір төбесіндегі жазық бұрыштарының қосындысы 120 0 . 3 = 360 -тан кіші болмас еді. Бірақ бұл мүмкін емес, өйткені дөңес көпжақтың өрбір төбесіндегі барлық жазық бұрыштардың қосындысы 360 0 -тан кіші. Осы себепті дұрыс көпжақтың әрбір төбесі үш, төрт немесе бес тең қабырғалы үшбұрыштардың, не үш квадраттың, не үш дұрыс бесбұрыштың төбесі болуы мүмкін. Басқа мүмкін жағдай жоқ.
Осыған сөйкес мынадай дұрыс көпжақтар аламыз:
Дұрыс тетраздр (1-сурет) (біз дұрыс тетраэдр мен дұрыс үшбұрышты пирамиданы ажыратып айтамыз.
Дұрыс тетраэдрдің жақтары - дұрыс ұшбұрыштар, оның әрбір төбесінде үш қыры тоғысады. Дұрыс тетраэдр барлық қырлары тең болатын үшбұрышты пирамида.
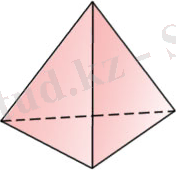
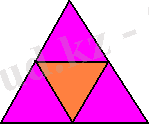
Барлық қырлары тең дұрыс тетраэдрден дұрыс үшбұрышты пирамиданың өзгешелігі оның бүйір қырлары бір-біріне тен болғанмен, олар табанының кабырғаларына тең болмауы мүмкін. ) төрт теңқабырғалы үшбұрыштан тұрады. Оның әрбір төбесі үш үшбұрыштың төбесі болып табылады. Демек, әрбір төбедегі жазық бұрыштардың қосындысы 180°-қа тең.
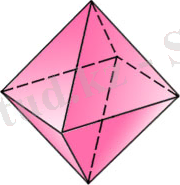
Дұрыс октаэдр (2-сурет) сегіз теңқабырғалы үшбұрыштан құралған. Октаэдрдің әрбір төбесі төрт үшбұрыштың төбесі болып табылады. Демек, әрбір төбедегі жазык бұрыштардың қосындысы 240 0 -ка тең. Октаэдрдің жақтары - дұрыс үшбұрыштар, оның әрбір төбесінде олар төртеуден тоғысады. Грек тілінен аударғанда, октаэдр - «сегіз жақты» деген мағына береді.
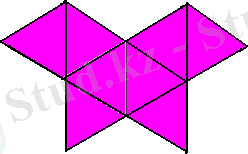
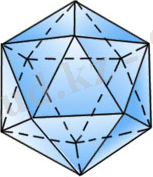
Дұрыс икосаэдр (3-сурет) жиырма тең қабырғалы үшбұрыштан құралған. Икосаэдрдің жақтары дұрыс үшбұрыштар, оның әрбір төбесінде олар бесеуден тоғысады. Грек тілінен аударғанда, икосаэдр -«жиырма жақты» деген мағына береді. Ендеше, әрбір төбедегі жазық бұрыштардың қосындысы 300 0 -қа тең.
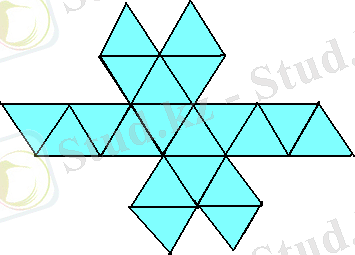
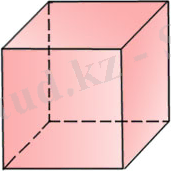
Куб (гексаэдр) (4-сурет) алты квадраттан құралған. Кубтың барлық жақтары квадраттар, оның әрбір төбесінде үш қыры тоғысады. Куб - барлық қырлары өзара тең тікбұрышты. Ендеше, өрбір төбедегі жазық бұрыштардың қосындысы 270°-қа тең.

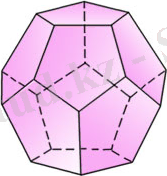
- Дұрыс додекаэдр(5-сурет) он екі дұрыс бесбұрыштан күралған. Додекаэдрдің жақтары - дұрыс бесбұрыштар, оның әрбір төбесінде олар үшеуден тоғысады. Грек тілінен аударғанда, додекаэдр- «он екі жақты» деген мағына береді. Ендеше, өрбір төбедегі жазық бұрыштардың қосындысы 3240-қа тең.
Дұрыс көпжақтардың осы аталып өткен бес түрінен басқа түрлері жоқ.
Дұрыс көпжактардың симметрия элементтерін карастырайық.
Дұрыс тетраэдрдің
(6-сурет)
симметрия центрі жок.
Қарама-қарсы қырларының орталары арқылы өтетін түзу оның симметрия осі болып табылады.
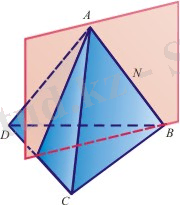
АВСD
дұрыс тетраэдрінің
АВ
қыры арқылы және қарама-қарсы жатқан
СD
қырына перпендикуляр өтетін α жазықтығы симметрия жазықтығы болып табылады (2-сурет) . Дұрыс тетраэдрдің үш симметрия осі және алты симметрия жазықтығы бар.
Сырттай сызылған сфера радиусы:
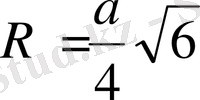
Іштей сызылған сфера радиусы:
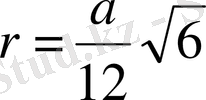
Бет ауданы:
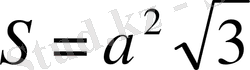
Тетраэдр көлемі:
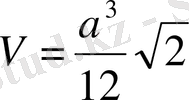
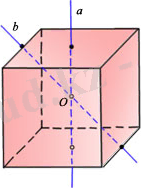
Куб диагональдарының қиылысу нүктесі - оның жалғыз ғана симметрия центрі болып табылады. Қарама-қарсы жатқан жақтардың центрлері және бір жақта жатпайтын қарама-қарсы екі қырдың орталары арқылы өтетін а жөне b түзулері оның симметрия осьтері болып табылады (7-сурет) .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz