Дифракция құбылысы

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

М. Х. ДУЛАТИ АТЫНДАҒЫ ТАРАЗ ӨҢІРЛІК УНИВЕРСИТЕТІ

«ҰСТАЗ» ИНСТИТУТЫ

Кафедра: Физика және IT

КУРСТЫҚ ЖҰМЫС

Тақырыбы: Дифракцияның құбылысын түсіндіру әдістемесі

Тобы: Ф18-1

Курс: 3

Қабылдаған: Сембиева Ақбота

Орындаған: Абдықапар Еркемай

Тараз - 2020ж.

Мазмұны:

Кіріспе . . .

I. Негізі бөлім

1. 1. Жалпы дифракция . . .

II. Дифракция құбылысы . . .

2. 1. Гюгенс-Френель принципі. .

2. 2. Тотығысатын сәулелер дифракциясы

2. 3. Параллель сәулелердің дифракциясы

2. 4. Дифракциялық решеткалар

Қорытынды . . .

Пайдаланылған әдебиеттер . . .

Кіріспе

Жарық дифракциясы деп жарық толқындарының өзінің алдында кездескен кедергілері орап кету қабілетін айтады. Дифракция құбылысы жарықтың толқындық қасиетінің айқын дәлелі болып табылады. Бұл құбылыс геометриялық оптика заңдылықтарының қай кезде бұзылатындығына нұсқайды.

Дифракцияның сандық теориясы, яғни бұл құбылыстың әсерінен экрандағы жарық интенсивтілігінің өзгеріп таралуын түсіндіру Гюгенс-Франель принципіне негізделген. Бұл негіз былай дейді:

1. Жарық толқындары келіп жеткен беттің әрбір нүктесі өз кезегінде жаңа толқын көздері болып табылады.

2. Бұл жаңа толқын кездері бір-біріне когерентті. Ал кеңістіктің кез-келген нүктесіндегі жарықтың интенсивтілігі осы когерентті жаңа көздерден тараған толқындардың интерференциясының салдары болып табылады.

Гюгенс-Френель принципі дифракциялық бейнелермен қатар жарықтың түзу сызық бойымен таралу себебін де түсіндіреді.

Жарық дифракциясының бір жарқын мысалы оның тар жолақ саңылау арқылы өткен кездегі дифракциясы. Бірақ, бұл жағдайдағы дифракциялық суреттің солғындау болуы оның нақтылы мақсаттарда қолдануда қиындықтар туғызады. Мұндай кемшіліктер дифракциялық тор деп аталатын қондырғыда жоқ.

Дифракциялық тор деп бір-біріне жақын, әрі паралллель орналасқан тар жолақ саңылаулар жүйесінен тұратын спектральдық құралды айтады.

Мұндағы а-күңгірт жолақтың ені, b-саңылаудың ені, ал d=a+b - дифракциялық тордың тұрақтысы деп аталады. Қазіргі кезде қолданылатын дифракциялық торлардың бір миллиметіріне 2000-ға дейін саңылаулар салынады. Гюгенс-Френель принципіне сәйкес мұндай әрбір саңылау өз кезегінде жаңа когерентті толқын көздері болып табылады да бұл көзден туындылаған толқындар бір-бірімен интерференцияланады. Егер дифракциялық торға перпендикуляр бағытта параллель жарық сәулелері түсетін болса, онда линзаның фокальдық жазықтығында орналсан экранда қандай да бір $\varphi$ бұрышымен дифракциялық максимумдар байқалады.

Дифракциялық торлар жазықты спектерлерге жіктеу үшін, сонымен қатар жарықтың белгісіз толқын ұзындығын анықтау үшін де қолданылады. Нақтылы зерттеулерде бір өлшемді торлармен қатар екі өлшемді торлар да жиі қолданылады. Екі өлшемді торлар деп жолақтарын бір - біріне перпендикулляр орналстырып, беттестірген екі жәй тордан тұратын жүйені айтады.

I. Негізі бөлім

Дифракция (лат. dіfractus - сындырылған) - механикалық, дыбыс және жарық толқындарының өздерінің толқын ұзындығымен шамалас тосқауылды орап өтуі, сондай-ақ сұйықтық пен газ молекулаларының немесе кристалл, сұйықтық, т. б. микробөлшектерінің электрондар, нейтрондар.

Laser Interference.JPG

Жарық дифракциясы - жарық толқындарының мөлшері сол толқындардың ұзындығымен қарайлас тосқауылды (тар саңылау, жіңішке сым, т. б. ) орап өту құбылысы . Жарық дифракциясы болуы үшін, мұның үстіне, жарық түскен дененің айқын шекарасы болуы да тиіс. Дифракция жарыққа ғана тән емес, басқа да толқындық процестерде де байқалады (мысалы, [механикалық толқынмеханикалық толқындардың жолында кездескен тосқауылды орап өтуі, т. б. ) . Жарық дифракциясы кезінде жарықтың түзу сызық бойымен таралу заңы, яғни геометриялық оптиканың негізгі заңдары бұзылады. Жарық толқындарының ұзындығы өте аз болғандықтан қалыпты жағдайда Жарық дифракциясы байқалмайды. Жарық дифракциясы - жарықтың толқындық қасиетін дәлелдейтін негізгі құбылыстардың бірі. Бұл құбылысты 17 ғ-да италиялық физик және астроном Ф. Гримальди (1618 - 1663) ашты, ал оны француз физигі О. Френель (1788 - 1827) түсіндірді (1812) . Френель Жарық дифракциясын екінші реттік толқындардың интерференциялану нәтижесі деп тұжырымдаған болатын. Жарық дифракциясының жуық теориясы Гюйгенс - Френель принципіне негізделген. Зоналар (аймақтар) әдісі деп аталатын бұл көрнекі әдіс бойынша толқындық бет ойша дөңгелек аймақтарға бөлінеді. Осы аймақтардан таралып бір-біріне қабаттасуы кезінде интерференцияланған элементар толқындардың амплитудалары мен фазалары есепке алынады. Нүктелік жарық көзінен шыққан жарық, күңгірт экранның кішкене дөңгелек саңылауынан немесе күңгірт дөңгелек экранның шетінен өткенде, концентрлі

шеңбер тәрізді дифракциялық жолақтар пайда болды. Егер саңылаудан өткен аймақтар саны жұп болса, онда дифракциялық - толқын ұзындығы), ал

параллель сәулелер дифракциясы: b шарттарын қанағаттандырады. Соңғы жағдайда саңылауға түскенλбейненің центрінде қараңғы дақ, ал тақ болса - жарық дақ секілді көрінеді. Дифракциялық жолақтардың арасы жарықтың толқын ұзындығына байланысты анықталады. Жарық дифракциясының сфералық толқындар дифракциясы (Френель дифракциясы) және параллель сәулелер дифракциясы (Фраунгофер дифракциясы) деп аталатын екі түрі бар. Френель аймағының мөлшерімен шамалас сфералық толқындардың дифракциясы: (мұндағы b - саңылаудың мөлшері, - бақылау нүктесінің экраннан қашықтығы, параллель жарық сәулелер =0) мәндерінде болады. Жарық дифракциясы нәтижесінде ұзын толқынды сәулелер көбірек, қысқа толқынды сәулелер азырақ бұрылады, яғни күрделі жарық толқын ұзындықтары бойынша жіктеледі. Басқаша айтқанда, дифракциялық спектрлер пайда болады. Кейбір спектрлік приборлардың жұмыс істеу принципі осы құбылысқа негізделген. Жарық дифракциясының көмегімен оптикалық приборлардың (ϕ=0 (яғни ϕ/b (m =1, 2, 3, . . . ) . Жарықталынудың ең үлкен шамасы m=0 және sіnλ=mϕ бұрышының өзгеруіне сәйкес болып экран бетінде өзгеріп отырады: sіnϕ/b) ажырайды. Тар саңылау арқылы өткен монохромат жарықтың параллель шоғы экранға түскенде, қарқындылығы тез кемитін, алма-кезек ауыса орналасқан жарық және қараңғы жолақтар пайда болады. Егер жарық саңылау жазықтығына перпендикуляр бағытта түссе, онда экрандағы жолақтар орталық жолаққа симметриялы болып орналасады (2-сурет) . Ал экранның жарықталынуы λ ∼ ϕшоғы алшақтау бұрышымен (телескоптардың, микроскоптардың, т. б. ) ажыратқыштық шамасы, сондай-ақ, лазер сәулесінің жинақтылығы анықталады.

II. Дифракция құбылысы

Дифракция құбылысы жарықтың толқындық сипаты білінетін құбылыстардың біреуі дифракция құбылысы болады. Дифракция деп жарықтың түсусызықты жолдан бұрылу құбылысы айтылады. Жарықтың осындай қасиеті бар екендігін мынадай тәжірибек жасап, білуге болады. Егер бір тар саңылаудан өткен жарық шоғының жолында саңылаудан 40 см жерде, оған параллель етіп тартылған дм-і 0, 2мм-дей жіңішке сым тұрған болса, сонда екі мертдей жердегі ақ экранға түскен сымның геометриялық көлеңкесінің дәл ортасына жіңішке ақ жолақ пайда болады. Бұл тәжірибеден жарық толқыны сымды орағытып барып көлеңке алқабына түскені байқалады. Демек, бөгетке кездесіп жарықтың жолы қисаяды. Бұл ретте орсы физигі В. Х. Аркадьев мынадай тәжірибе жасаған. Диаметрі 1-1, 97мм инеге одан 24, 17м қашықтықта тұрған өлшемдері 0, 7х0, 7мм саңылау арқылы толқын ұзындығы 0, 46мкм монохромат жарық шоғын түсірген иненің екінші жағына 15, 47м жерге фотопластинка қойып сол ине көлеңкесінің фотосуретін түсіріп алған. Сонда, ине көлеңкесінің дәл ортасында жіңішке жарық жолақ, екі жағында онымен қатарласа орналасқан бірнеше жарық және қара-қоңыр жолақтар байқалған. Бұдан жарық толқынының жолындағы инені айнала өтіп көлеңке алқабына барғаны байқалады.

Дифракция құбылысы тек жарыққа қана емес басқа да толқындық процестерге тән құбылыс. Мысалы, дыбыс толқындары да жолында кездескен бөгетті айнала бұрылып таралады биік үйдің бір жағынан шыққан дыбыс оның екінші жағынан да естіледі, өйткені, дыбыс толқыны үйдің бұрышына жетіп бұрылады да, қалқаланып тұрған алқапқа барады. Басқаша айтқанда, дифракцияланады. Бұл ретте бір ескерте кететін нәрсе: жарықтың тридифркциясы кәдімгі жағдайларда байқалмайды. Оны тек ерекше жағдайларда ғана байқауға болады.

Жарықтың толқындық сипаты білінетін құбылыстардың біреуі дифракция құбылысы болады. Дифракция деп жарықтың түсу сызықты жолдан бұрылу құбылысы айтылады. Жарықтың осындай қасиеті бар екендігін мынадай тәжірбие жасап білуге болады. Егер бір тар саңлаудан өткен жарық, шоғының жолында, саңылаудан 40 см жерде, оған параллель етіп тартылған диаметрі 0, 2 миллиметрдей жіңішке сым тұрған болса, сонда 2 метрдей жердегі ақ экранға түскен сымның геометриялық көлеңкесінің дәл ортасына жіңішке ақ жол пайда болады.

Бұл тәжірбиеден жарық толқыны сымды орағытып барып көлеңке алқабына түскені байқалады. Демек бөгетке кездесіп жарықтың жолы қисаяды.

Бұл ретте орыс физигі В. К. Аркадьев мынадай тәжірбие жасаған. Диаметрі 1, 97 мм инеге одан 24, 17 м қашықтықта тұрған өлшемдері 0, 7*мм саңылау арқылы толқын ұзындығы 0, 46 мкм жерге, фотопластинка қойып сол ине көлеңкесінің фотосуретін түсіріп алған. Сонда ине көлеңкесінің дәл ортасында жіңішке жарық жолақ, екі жағында сонымен қатарласа орналасқан бірнеше жарық жәнеқара қоңыр жолақтар байқалған. Бұдан жарық толқынының жолындағы денені айнала өтіп көлеңке алқабына барғаны байқалады.

Дифракция құбылысы тек жарыққа ғана емес, басқа да толқындық процестерге тән құбылыс. Мысалы, дыбыс толқындары да жолында кездескен бөгетті айнала бұрылып таралады. Биік үйдің бір жағынан шықққан дыбыс оның екінші жағынан да естіледі, өйткені дыбыс толқыны үйдің бұрышына жетіп бұрылады да қалқаланып тұрған алқапқа барады, басқаша айтқанда дифракцияланады. Бұл ретте бір ескерте кететін нәрсе: жарықтың дифракция кәдімгі жағдайларда байқалмайды, оны тек ерекше жағдайларда ғана байқауға болады.

Дифракция - жарықтың толқындық сипаты білінетін құбылыс. Тәжірибелік деректер . Бізге байқалатын көптеген құбылыстар жарықтың түзу сызықты таралатындығын көрсетеді. Күн сәулесі, лазер сәулесі, прожектор сәулесі- бұлар түзу сызықтар бойынша таралу сезімін туғызады. Түзу сызықты таралу - жарықтың ең басты және ең айқын қасиеттерінің бірі. Сөз жоқ, дәл осы жағдай өз уақытында жарық - бөлшектер ағыны деген түсініктің қалыптасуына негіз болған. Екінші жағынан, түзу сызықты жарық сәулесінде толқынға ұқсайтындай ешқандай белгі жоқ сияқты болып көрінеді.

Дегенмен, кейбір өте нәзік оптикалық құбылыстар мен тәжірибелер жарықтың түзу сызықты таралу заңының бұзылатындығын көрсетеді. Мәселен, Күн сәулесінің немесе лазер сәулесінің әрқашан, аз да болса, бірақ шектеулі жинақсыздануы байқалады. Жарық шоғының шекарасы, жарық пен көлеңке арасындағы шекара ешқашанда айқын болмайды, әрқашан кішкене болса да оның шектеулі ені болады.

Дифракция ұғымы оптикада жарықтың түзу сызықты таралуы бұзылуымен байланыстырылады. А. Зоммерфельд (1868-1951) дифракцияға “жарықтың шағылуы немесе сынуымен байланысты емес, түзу сызықты таралудан кез-келген ауытқуы” деген анықтама берген.

Тар мағынасында дифракция деп толқынның бөгетті айналып өту құбылысын айтады. Мұндай құбылыстар ұзын толқындар үшін, мысалы, дыбыс толқындары немесе су бетіндегі толқындар үшін жақсы белгілі. Толқындар теориясында дифракция деп толқынның таралуына кедергі

(тосқауылдар) жолыққанда толқындық өрісте пайда болатын құбылыстардың

барлық жиынтығын айтады. Ең соңында, жарықтың интерференция ұғымын

пайдаланып, былай деуге болады: дифракция - бұл шектеулі жарық шоқтарындағы интерференция.

1. 1. Гюгенс-Френель принципі

Гюйгенс - Френель принципі - екінші ретті қөздерден таралған толқын интерференциясын есептеу жолымен дифракциялық суреттің интенсивтілігін табудың жуық тәсілі.

Сипаттамасы

Гюйгенс-Френель принципі-1678 жылы Христиан Гюйгенс енгізген принциптің дамуы: фронттың әр нүктесі (Толқынға жеткен беттер) сфералық толқындардың қайталама (яғни жаңа) көзі болып табылады. Барлық екінші көздердің толқындарының айналмалы фронттары келесі сәтте толқынның алдыңғы жағына айналады.

Гюйгенс принципі геометриялық оптика заңдарына сәйкес келетін толқындардың таралуын түсіндіреді, бірақ дифракция құбылысын жеткілікті толық, тіпті сандық түрде түсіндіре алмайды. Френель 1815 жылы Гюйгенс принципін толықтырып, қарапайым толқындардың үйлесімділігі мен кедергісі туралы идеяларды енгізді, бұл Гюйгенс - Френель принципі негізінде дифракциялық құбылыстарды қарастыруға мүмкіндік берді.

Гюйгенс-Френель принципі келесідей тұжырымдалған:

Толқын фронтының әр элементін екінші сфералық толқындарды тудыратын екінші реттік бұзылыстың орталығы ретінде қарастыруға болады, ал кеңістіктің әр нүктесінде пайда болған жарық өрісі осы толқындардың кедергісімен анықталады. Неміс физигі Густав Кирхгоф Гюйгенс принципіне қатаң математикалық көрініс беріп, оны Кирхгоф интегралдық теоремасы деп аталатын теореманың жуық формасы деп санауға болатындығын көрсетті.

Біртекті изотропты кеңістіктегі нүкте көзі толқынының алдыңғы жағы-сфера. Нүктелік көзден таралатын толқынның сфералық фронтының барлық нүктелеріндегі қозу амплитудасы бірдей.

Гюйгенс принципін одан әрі жалпылау және дамыту-қазіргі кванттық механиканың негізі ретінде қызмет ететін траектория бойынша интегралдар арқылы тұжырымдау.

Жарық дифракциясыт бірақ ең көп таралған мағынада-мөлдір емес денелердің (экрандардың) шекарасын жарық сәулелерімен айналдыру; жарықтың геометриялық көлеңке аймағына енуі. Жарықтың дифракциясы сәулелер ағынының тығыздығының күрт өзгеру аймақтарында көрінеді: каустикке жақын, линзаның фокусы, геометриялық көлеңке шекаралары және т. б. толқындардың дифракциясы біртекті емес ортадағы толқындардың таралуы мен шашырау құбылыстарымен тығыз байланысты.

Дифракция дегеніміз-өлшемдері толқын ұзындығымен салыстырылатын және геометриялық оптика заңдарынан ауытқулармен байланысты өткір гетерогенділігі бар ортада жарықтың таралуы кезінде байқалатын құбылыстардың жиынтығы.

Кедергілердің дыбыстық толқындармен айналуы (дыбыстық толқындардың дифракциясы) біз үнемі байқаймыз (үйдің бұрышынан дыбысты естиміз) . Жарық сәулелерінің дифракциясын бақылау үшін ерекше жағдайлар қажет, бұл жарық толқындарының қысқа ұзындығына байланысты.

Кедергі мен дифракция арасында айтарлықтай физикалық айырмашылықтар жоқ. Екі құбылыс толқындардың суперпозициясы нәтижесінде жарық ағынын қайта бөлуден тұрады.

Дифракция құбылысы Гюйгенс принципімен түсіндіріледі, оған сәйкес Толқынға жеткен әр нүкте екінші толқындардың орталығы ретінде қызмет етеді, ал осы толқындардың конверті келесі сәтте толқын фронтының орнын белгілейді.

Тегіс толқын әдетте мөлдір емес экрандағы тесікке түссін (сурет. 9. 1) . Саңылаумен бөлінген толқын фронтының әр нүктесі қайталама толқындардың көзі ретінде қызмет етеді (біртекті изотоптық ортада олар сфералық) .

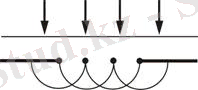
Сур. 9. 1

Президентіміз огибающую екінші реттік толқындардың үшін біраз уақытына, көреміз, не фронт толқын келіп облысқа геометриялық қабақ бояуы, т. е. толқын-батыс жағымен айналады шетінен тесік.

Гюйгенс принципі толқын фронтының таралу бағыты туралы мәселені ғана шешеді, бірақ әртүрлі бағытта таралатын толқындардың амплитудасы мен қарқындылығы туралы мәселені қозғамайды. Жарықтың толқындық табиғатын бекітуде шешуші рөлді XIX ғасырдың басында О. Френель атқарды. Ол дифракция құбылысын түсіндіріп, оны сандық есептеу әдісін берді. 1818 жылы ол дифракция құбылысын және оны сандық есептеу әдісін түсіндіргені үшін Париж академиясының сыйлығын алды.

Френель Гюйгенс принципіне физикалық мағына беріп, оны қайталама толқындардың араласуы идеясымен толықтырды. Дифракцияны қарастырған кезде Френель дәлелсіз қабылданған бірнеше негізгі ережелерден басталды. Бұл тұжырымдардың жиынтығы Гюйгенс-Френель принципі деп аталады.

Гюйгенс принципіне сәйкес толқынның әр алдыңғы нүктесін қайталама толқындардың көзі ретінде қарастыруға болады.

Френель бұл принципті айтарлықтай дамыды.
Бір көзден шыққан толқынның алдыңғы жағының барлық қайталама көздері бір-біріне сәйкес келеді.
Толқын бетінің тең аудандары бірдей қарқындылықты (қуатты) шығарады.
Әрбір екінші көз жарықты негізінен сыртқы қалыпты бағытта осы кезде толқын бетіне шығарады. Қалыпты α бұрышын құрайтын бағыттағы қайталама толқындардың амплитудасы α бұрышы неғұрлым аз болса және нөлге тең болса .
Екінші көздер үшін суперпозиция принципі әділетті: толқын бетінің кейбір бөлімдерінің сәулеленуі басқалардың сәулеленуіне әсер етпейді (егер толқын бетінің бір бөлігі мөлдір емес экранмен жабылған болса, екінші толқындар экран болмағандай ашық жерлерде шығарылады) .

2. 2. Тотығысатын сәулелер дифракциясы

Осы уақытқа дейін біз кедергіден ( Френель дифракциясы ) соңғы қашықтықта орналасқан бақылау нүктесінде дифракциялық суретті зерттей отырып, сфералық толқындардың дифракциясын қарастырдық.

Дифракция түрі, онда дифракциялық сурет параллель сәулелермен түзіледі, Фраунхофердің дифракциясы деп аталады. Егер көзі мен экраны шексіздікте болса, параллель сәулелер пайда болады. Екі линза іс жүзінде қолданылады: біреуінің фокусында - жарық көзі, ал екіншісінің фокусында - экран.

Фраунхофердің дифракциясы Френельдің дифракциясынан түбегейлі өзгеше болмаса да, бұл іс жүзінде маңызды, өйткені дифракцияның бұл түрі көптеген дифракциялық құрылғыларда қолданылады (мысалы, дифракциялық тор) . Сонымен қатар, мұнда математикалық есептеу оңайырақ және сандық есепті соңына дейін шешуге мүмкіндік береді (біз Френельдің дифракциясын сапалы қарастырдық) .

Бір саңылаудағы жарықтың дифракциясы

Үздіксіз экранда бос орын болсын: жарықшақтың ені, жарықшақтың ұзындығы (парақтың жазықтығына перпендикуляр) (сурет. 9. 5) . Жарықтың параллель сәулелері саңылауға түседі. Есептеуді жеңілдету үшін АВ жазықтығында құлаған толқындардың амплитудасы мен фазалары бірдей деп санаймыз.

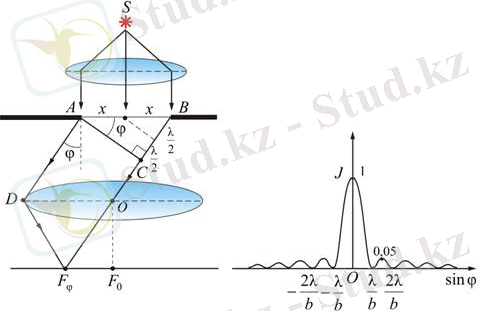
Сур. 9. 5

Көршілес аймақтардан келетін сәулелер арасындағы оптикалық айырмашылық тең болатындай етіп алшақтықты Френель аймақтарына бөлеміз.

Егер мұндай аймақтардың жұп саны саңылаудың еніне сәйкес келсе, онда нүктеде (линзаның бүйірлік фокусы) қарқындылықтың минимумы байқалады, ал егер тақ аймақтар саны болса, онда қарқындылықтың максимумы болады:

${\ \ \ \ \ \ \ \ bsin}\varphi = \pm$ 2 $m\frac{\lambda}{2}\, \ \ \ \ \ \ \ \ \ \ \$ - қарқындылық минимумының шарты; (9. 4. 1)

b $\sin ф = \pm (2m + 1) \frac{\lambda}{2}$ - максималды қарқындылық шарты (9. 4. 2)

Сурет нүктенің негізгі фокусына қатысты симметриялы болады $F_{0}$ . Плюс және минус белгісі бір бағытта немесе басқа бағытта есептелген бұрыштарға сәйкес келеді. Жарықтың қарқындылығы J $\sim A^{2}$ . Көрсетілгендей күріш. 9. 5, қарқындылықтағы орталық максимум басқалардан асып түседі.

Саңылау енінің әсерін қарастырыңыз.

Себебі минимумның жағдайы көрінеді, демек b $\sin ф = \pm m$ $\lambda$

$\sin ф = \frac{m\lambda}{b}$ (9. 4. 3)

Бұл формуладан B саңылауының енінің жоғарылауымен минимумдардың позициялары орталыққа ауысатындығын, орталық максимум күрт өзгеретінін көруге болады.

B саңылауының ені азайған кезде бүкіл сурет кеңейеді, бұлыңғыр болады, орталық жолақ та кеңейіп, экранның көп бөлігін алады және оның қарқындылығы төмендейді.

2. 3. Параллель сәулелердің дифракциясы

Фраунгофер дифракциясы (немесе жазық жарық толқындарының дифракциясы немесе параллель сәулелердегі дифракция) жарық көзі мен бақылау нүктесі дифракцияны тудырған кедергіден шексіз алыстаған жағдайда байқалады.

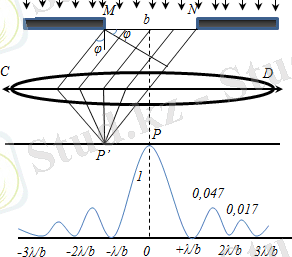
Фраунгофердің дифракциясын бақылау үшін нүктелі көзді жинаушы линзаның фокусына орналастыру қажет, ал дифракциялық суретті кедергінің артына орнатылған екінші жинаушы линзаның фокустық жазықтығында зерттеуге болады.

Монохроматикалық толқын шексіз ұзын тар саңылаудың жазықтығына қалыпты түсіп кетсін ( $l \gg b$ ), $l$ - ұзындығы, b-ені. 1 және 2 сәулелер арасындағы инсульт айырмашылығы φ бағытта

$\mathrm{\Delta} = NF = b\sin\varphi$

Разобьем волновую беті учаскесінде саңылау МN арналған френельдің зоналық әдісі бар түрі кесінділер, параллель ребру М саңылау. Әр жолақтың ені осы аймақтардың шеттерінен жүріс айырмашылығы Егер Френель аймақтарының саны тақ болса

λ/2-ге тең болатындай етіп таңдалады, яғни. Себебі саңылаудағы Жарық қалыпты түрде түседі, содан кейін жарықшақтың жазықтығы толқынның

алдыңғы жағымен сәйкес келеді, сондықтан жарықшақтың жазықтығындағы барлық нүктелер фазалық түрде өзгереді. Саңылау жазықтығындағы қайталама толқындардың амплитудасы тең болады, өйткені таңдалған Френель аймақтары бірдей аудандарға ие және бақылау бағытына бірдей бейім.

Саңылаудың еніне сәйкес келетін Фрезель $\mathrm{\Delta}/($ λ /2) аймақтарының саны φ бұрышына байланысты.

Френельдің дифракциясындағы минимум жағдайы:

Егер Френель аймақтарының саны жұп болса

$\frac{\mathrm{\Delta}}{\lambda + 2} = \pm$ 2 $m$ немесе ${bsin}\varphi = \pm$ 2 $m\frac{\lambda}{2}\,$