Теңдеулер мен теңдеулер жүйесін шешу әдістері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 24 бет
Таңдаулыға:

Курстық жұмыс
Ф 11.01-2020
1-баспа 25.06.2020

Қазақстан Республикасының білім жӘне ғылым министрлігі
М.Х. ДУЛАТИ АТЫНДАҒЫ ТАРАЗ ӨҢІРЛІК УНИВЕРСИТЕТІ

ҰСТАЗ ИНСТИТУТЫ

Мектепке дейінгі және бaстaуыш білім беру кафедрасы

КУРСТЫҚ Жұмыс

Математиканы оқыту әдістемесі пәні бойынша

Тақырыбы: Теңдеу

Білімгер:Мадиева Жансая Шаяхметқызы ПМНО18-1К
_____________
қолы

Жетекші:Сарыбекова Қ.Н.п.ғ.к., доцент
аты-жөні қызметі

Қорғауға жіберілді ____________________2020ж. ____ _________________

қолы

Жұмыс қорғалды __________________2020ж. бағасы __________________

жазбаша
Комиссия мүшелері: _________________________ ____________________
аты-жөні қолы

______________________________ ___ ________________
аты-жөні қолы

______________________________ ___ ________________
аты-жөні қолы

Тараз 2020
Курстық жұмыс
Ф 11.01-2020
1-баспа 25.06.2020

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
М.Х. ДУЛАТИ АТЫНДАҒЫ ТАРАЗ ӨҢІРЛІК УНИВЕРСИТЕТІ
МЕКТЕПКЕ ДЕЙІНГІ ЖӘНЕ БAСТAУЫШ БІЛІМ БЕРУ кафедрасы

ПМНО 18-1К тобының білімгеріне Мадиева Жансая Шаяхметқызы. курстық жоба (жұмыс)
ТАПСЫРМА
МАТЕМАТИКАНЫ ОҚЫТУ ӘДІСТЕМЕСІ пәні бойынша

1. Тақырыбы: Теңдеу

2. Тапсырманың арнайы нұсқауы - курстық жұмысты университеттің талаптарына сай рәсімдеу

3.Есепке-түсініктеме жазбаларының негізгі тараулары (жұмыстары)
Орындау кестесі

Көлемі, %
Орындау уақыты
Кіріспе
10%
29.09
І. ТЕҢДЕУЛЕР ЖӘНЕ ТЕҢДЕУЛЕР ЖҮЙЕСІН ОҚЫТУ ӘДІСТЕМЕСІНІҢ МАЗМҰНЫ
30%
01.10
1.1 Теңдеулер және теңдеулер жүйесінің ұғымы
5%
03.10
1.2 Теңдеулерді оқыту әдістемесі
5%
05.10
ІІ ТЕҢДЕУЛЕРДІ ОҚЫТУ ӘДІСТЕМЕСІ АРҚЫЛЫ ШЫҒАРУҒА ҮЙРЕТУ ЖОЛДАРЫ

20%
07.10
2.1 Теңдеулер мен теңдеулер жүйесін шешу әдістері

09.10
2.2 Теңдеулер құру арқылы есептер шығару
10%
13.10
Қорытынды
10%
03.11
Пайдаланылған әдебиеттер
10%
29.09
Жобаның (жұмысты) жинақтау мерзімі

Қорғау

Кафедра мәжілісінде бекітілген 24.092020 ж. хаттама № 2
Жетекшісі:п.ғ.к., доцент ______ Сарыбекова Қ.Н
қызметі қолы аты-жөні

Тапсырманы орындауға қабылдадым _______

МАЗМҰНЫ:

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .3

І ТЕҢДЕУЛЕР ЖӘНЕ ТЕҢДЕУЛЕР ЖҮЙЕСІН ОҚЫТУ ӘДІСТЕМЕСІНІҢ МАЗМҰНЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... 5
1.1 Теңдеулер және теңдеулер жүйесінің ұғымы ... ... ... ... ... ... ... .. ... ... ... ... ...5
1.2 Теңдеулерді оқыту әдістемесі ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ...7

II ТЕҢДЕУЛЕРДІ ОҚЫТУ ӘДІСТЕМЕСІ АРҚЫЛЫ ШЫҒАРУҒА ҮЙРЕТУ ЖОЛДАРЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .15
2.1. Теңдеулер мен теңдеулер жүйесін шешу әдістері ... ... ... ... ... ... ... ...15
2.2. Теңдеулер құру арқылы есептер шығару ... ... ... ... ... ... ... . ... ... ...19

ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .22
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... . ... ... ... ... ... ... ..23

КІРІСПЕ
Теңдеуді терең түсініп меңгеру математикалық білімдерді одан әрі дамытуға, қоршаған ортадағы сан алуан құбылыстарға, терең мағыналы модельдер жасауға үйретеді. Теңдеулерді шешу оқушыларды еңбек сүйгіштікке тәрбиелейді. Қарастырылатын мәселерді ең тиімді, ұтымды, пайдалы жақтарынан зерттеуге үйретеді. Атқарылатын жұмыстарға терең, салыстырмалы түрде жан - жақты талдаулар жасай отырып, дұрыс жоспар құруға пәрменді көмегін тигізеді. Орындалған жұмыстардың нәтижелеріне сыншыл көзқараспен қорытындылар жасауға үйретеді.
Оқу процесінде есеп шығару математиканы оқыту мақсаты ретінде де, оны үйрету әдісі ретінде де бой көрсетеді.
Математикалық есеп дегеніміз - математикадағы заңдылықтар, ережелер мен тәсілдер негізінде оқушылардын ойы мен іс-әрекетін талап ететін және математикалық білімді меңгеруге, оларды практикада қолдана білуге дағдыландыруга, ойлау қабілетін дамытуға бағытталған ситуация.
Сондықтан есеп шығару математикалық ұғымдарды қалыптастырып, байытуга оқушылардың математикалық ойлауын өрісіріуге, білімдерін пракикада қолдануға, табандылық, ізденгіштік, еңбек сүйгіштік қасиеттерін тәрбиелеуге жол ашады. Сонымеи бірге, есеп шығару процесінде оқушылар практикалық біліктер мен өмірде өздеріне керекті дағдыларды игерсді пайдалы фактілсрмен танысады. Өмірде жиі кездесетін шамалардың арасындагы байланыстар мен тәуелділіктерді тагайындауға үйренеді. Математикалық есептер: а) жаңа математикалық ұғымдар мен мағлұматтарды үйрету; ә) пракгикалық іскерліктер мен дағдыларды қалыптастыру; б) білімнің тереңдігі меи жаяндылығын тексеру; в) проблема қою және проблемалық ахуал туғызу; г) материалды пысықтау, жалпылау және қайталау; д) оқушылардың шығармашылық қабілетін тәрбиелеу үшін пайдалынады.
Есеп оқушыларды жана математикалық біліммен қаруландырып, қалыптасқан іскерліктері мен машықтарын жүйелеуге және нақтылауға көмектеседі. Бастауыш сыныпта арифметикалық және геометриялық мазмұнды құрылымы күрделі емес есептер қолдаиылады.
Математиканы оқытудың жалпы системасында есептер шығару тиімді жаттығулардың бір түрі болып табылады.
Есептер шығарудың ең әуелі балаларда толық бағалы математикалық ұғымдарды қалыптастыруда, олардың багдарлама аныктап берген теориялық білімді игеруде өте маңызды мәні бар.
Оқушылардың ойлау жүйесінің, ой қорытындыларының ұтымды логикалық жолымен дамуына кең жол салады. Олай болса, теңдеулерді шешуі мектеп математикасын басқа салалары сияқты, оқушылардың ойлау жүйесінің жас жеткіншектерге лайықты дамуына, оларды қоғамға, Отанына пайдалы азамат болып қалыптасуына лайықты пайдасын тигізеді.
Курстық жұмыстың өзектілігі. Алгебралық элементтерді бастауыш сыныптарда ұзақ уақыт бойы оқытылып бір-бірімен қолдануға бейім тұрақтығын да. Осының нәтижесінде білім стандарты мен оқу бағдарламалары деңгейінде білім, білік және дағдыларды қалыптастыруда кемшіліктер орын алуда. Теңдеу және оны шешу тәсілдері бастауыш сыныптарда оқытудың теориясы енгізіледі. Теңдік және теңсіздік туралы түсініктерін қайталау, сандарды, сандық және әріптік есептерді салыстыру дағдыларын дамыту. Математика курсының алгебралық есептерін шешуде құрамында ең болмағанда бір айнымалысы бар көпмүшені екі немесе бірнеше көпмүшелердің, немесе көпмүше мен бірмүшенің көбейтіндісі түрінде жазуға болады. Көпмүшелерді көбейткіштерге жіктеуде әр түрлі әдістерді пайдаланады, атап айтқанда ортақ көбейткішті жақша сыртына шығару; көпмүшенің ұқсас мүшелерін топтау; ауыстыру; қысқаша көбейту формуларын пайдалану және т.б. әдістер.
Курстық жұмыстың мақсаты. Ой өрiсi дамыған, сана сезiмi оянған, рухани ойлау дәрежесi биiк, математикадан бiлiм деңгейi жоғары, пәнге деген қызығушылығы мол, теориялық бiлiмдi терең түсiне алатын оқушыларды тәрбиелеп, теңдеулерді шешу жолдарын ашып көрсету.
Курстық жұмыстың зерттеу пәні: Есеп шығаруға теңдеуді оқытып үйрету үдерісі.
Курстық жұмысты зерттеудің болжамы: егер теңдеуді оқытудың пәндік теориялық және әдістемелік қолданылса онда осы мәселені оқытып үйретумен байланысты жұмыс жасау. Егер бастауыш сыныпта оқушыларға алгебралық материалдарды жетік меңгерте алсақ, онда олардың математикадан бiлiм деңгейi жоғарылайды және т.б пәндердi оқушылардың жетелей түсiнуiне, қазіргі заман талабына сай терең білім алуына ықпал жасайды.
Курстық жұмыстың міндеттері:
- теңдеу ұғымының мән-мағынасының оны шешу тәсілдер кезеңдерінің оларды оқытудың маңызын айту.
- білім стандартта, оқу бағдарламаларына және оқулықтарға зерттеу жұмысының мақсаты бастауыш сыныптар мұғалімдерінің теңдеу және оны шешу тәсілдерін оқыту.
Курстық жұмысты зерттеудің негізгі көздері: математиканың негіздері және математиканы бастауыш сыныптарда оқыту әдістемесі.
Курстық жұмыстың құрлымы. Курстық жұмыс кіріспеден, негізгі бөлімнен, төрт бөлімшелерден және қорытынды мен пайдаланылған әдебиеттер тізімінен тұрады.

І ТЕҢДЕУЛЕР ЖӘНЕ ТЕҢДЕУЛЕР ЖҮЙЕСІН ОҚЫТУ ӘДІСТЕМЕСІНІҢ МАЗМҰНЫ
1.1 Теңдеулер және теңдеулер жүйесінің ұғымы

Математиканы оқытудың білімдік мақсаты - барлық оқушыларды математиканың ғылыми негіздері туралы жүйелі біліммен және оларды толық, сапалы да берік игеруге қажетті біліктіліктермен, дағдылармен қаруландыру болып табылады. Осындай білім алу нәтижесінде оқушылардың ақыл-ойы дамиды, деңгейі кеңиді. Математиканың негізгі мазмұнын құрайтын оқыту материалдарынбіріктіретін, үйлестіретін, оның ғылымилығы және қолданбалығы принциптерін іске асыруға мүмкіндік беретін негізгі ұғымдар - теңдеулер мен теңсіздіктер. Осы ұғымдармен байланысты шығарылатын есептер оқушылардың логикалық ойлау, кеңістікті елестету, жеке бас қабілеттерін дамытуға бірден-бір себепші болатын басты құрал.
Алған білімдерін дәстүрлі емес жағдайларда қолдана білуге, өмірлік жоспарларын іске асыруда, жоғары сынып оқушыларының сапалы білім алуында теңдеулер жүйесін шешуді оқып-үйрену өте маңызды орын алады.
Теңдік, теңдеулер және теңсіздіктер түсінігі ерте заманнан өмір және практика қажеттілігінен туындаған болатын.[12]
Мысалы, осыдан 4000 жыл бұрын вавилондықтар геодезиялық, құрылыс салудың және әскери дайындық есептерін бірінші және екінші дәрежелі теңдеулер арқылы шығарған.
Осындай дәрежедегі теңдеулерді ежелгі Қытай мен Үнді ғалымдары да шығара білген. Теңдеулер арқылы шығарылатын есептер көне мәтіндерде кездеседі.
Ерте кезден бастап жер бөліктерінің ауданын табуға және әскери сипаттағы жер жұмыстарына, сонымен қатар астрономия және математиканың дамуына байланысты бірінші ғана емес, екінші дәрежелі теңдеулерді шешу қажеттілігі пайда болады.
Б.з.д. 2000 жыл бұрын вавилондықтардың қолжазбаларында толық емес квадрат теңдеулермен қатар

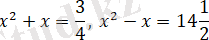
тәрізді толық квадрат теңдеулер де кездеседі.
(1)
түріне келтірілген квадрат теңдеулерді шешудің жалпы ережесін үндінің тағы бір ғалымы Брахмагупта (VIIғ.) берген (1) теңдеуінде a-дан басқа коэффициенттер теріс болуы мүмкін.
Теңдеулер және теңдеулер жүйесін қарастыру, оларды шешу мәселелері білімде және ғылымда кеңінен қарқынды қарастырыла бастады.Өйткені, осы тақырыптарды жақсы түсінген, саналы меңгерген оқушылар мектептік математика курсын сапалы және терең деңгейде оқып-үйрене алатын болады.
Мектеп курсында бұл тақырыптар жүйелі түрде екінші сыныптан бастап оқытылады, содан мектеп бітіргенше жалғастырылады. Сондықтан бұл тақырыптар мектеп математика курсы бойынша білім деңгейін тереңдетудің және оның сапасын жақсартудың негізгі арқауы және құралы болып табылады. Оған мына мысалдардан көз жеткізуімізге болады деп ойлаймын.[13]
Теңдеулер
Көрсеткіштік теңдеулер
Тригонометриялық теңдеулер

Трасценденттік теңдеулер
Алгебралық теңдеулер

Иррационал теңдеулер
Рационал теңдеулер

Бөлшек-рационал теңдеулер
Бүтін теңдеулер

Жоғары дәрежелі теңдеулер
Квадрат теңдеулер
Сызықтық теңдеулер

Логарифмдік теңдеулер

Анықтама. Теңдеудің түбірі деп теңдеуді дұрыс теңдікке айналдыратын айнымалының мәнін айтады.
Теңдеуді шешу дегеніміз - оның барлық түбірлерін табу немесе түбірлерінің жоқ екенін дәлелдеп көрсету.
Теңдеулерді шешкенде мына қасиеттер қолданылады:
1) егер теңдеудегі қосылғыштың таңбасын өзгертіп, бір бөлігінен екінші бөлігіне көшірсе, онда берілген теңдеумен пара - пар теңдеу шығады;
2) егер теңдеудің екі бөлігін де нөлге тең емес бір ғана санға көбейтсе немесе бөлсе, онда берілген теңдеумен пара - пар теңдеу шығады.
Анықтама. 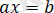түріндегі теңдеуді, мұндағы - айнымалы, a мен b - қандай да бір сандар, бір айнымалысы бар сызықтық теңдеу деп атайды Екі айнымалысы бар теңдеудің графигі деп координаталық жазықтықтың координаталары осы теңдеудің шешімдері болып табылатын барлық нүктелерінің жиынын айтады.
Анықтама. Екі айнымалысы бар теңдеулер жүйесінің шешімі деп жүйенің әрбір теңдеуін дұрыс теңдікке айналдыратын айнымалылар мәндерінің жұбын атайды.[11]
Екі айнымалысы бар теңдеулер жүйелерін шешу
Ауыстыру тәсілі. Екі айнымалысы бар екі сызықтық теңдеу жүйесін ауыстыру тәсілімен шешкенде:
* бір теңдеуден бір айнымалыны екіншісі арқылы өрнектейді;
* бұл алынған өрнекті екінші теңдеудегі осы айнымалының орнына апарып қояды;
* бұдан шыққан бір айнымалысы бар теңдеуді шешеді;
* екінші айнымалының сәйкес мәнін табады.
* Қосу тәсілі. Екі айнымалысы бар екі сызықтық теңдеу жүйесін қосу тәсілімен шешкенде:
* айнымалылардың біреуінің коэффициенттері қарама-қарсы сандар болып шығатындай етіп, лайықты көбейткіштер таңдап алады да, жүйенің теңдеулерін сол көбейткіштерге көбейтеді;
* алынған жүйе теңдеулерінің сол жақ және оң жақ бөліктерін мүшелеп қосады;
* шыққан бір айнымалылы теңдеуді шешеді;
* екінші айнымалының сәйкес мәнін табады.
Есептерді теңдеулер жүйесін құру арқылы шешу.
Теңдеулер жүйесін құру арқылы есептер шығарғанда қандай да бір белгісіз сандарды әріптермен белгілейді де, содан соң есептің артын пайдаланып, теңдеулер жүйесін құрады, бұл жүйені шешеді, шыққан нәтижені есептің шартына сәйкестендіріп түсіндіреді.[14]

1.2. Теңдеулерді оқыту әдістемесі
Бастауыш мектепте тендеулерді шешудің тәсілдерімен оқушыларды таныстыру 1 сыныпта басталады. Мұнда өзге қарапайым теңдеулерді шешу тәсілдері үйретіледі бір бөлігі - құрамында әріп бар өрнек, ал екінші бөлігі санды өрнек болатын теңдеулермен таныстыру бағытында жұмыстар жүргізіледі. Оқушылар теңдеулерді мысалдардың дербес түрі яғни "құрамында әріппен таңбаланған белгісіз болатын тендік" ретінде, ал теңдеуді шешу "оны тура санды теңдікке айналдыратын әріптің сәйкес мәнін табу" деп түсінуіне жету көзделеді.
Бастауыш сыныптарда бұл тақырыпты өтудегі негізгі мақсат оқушыларға теңдеу жайында түсінік беру, оның шешудің тәсілдерін оқып үйрету, тендеу құру арқылы есептер шығаруды үйрету, яғни қарапайым тендеулерді шешу дағдысының қалыптастырылуы.[15]
Бастауыш мектеп бағдарламасында теңдеулерді шешудің тәсілдерімен оқушыларды таныстыру I сыныпта □+4=7 қарастырылады да. Мұнда өте қарапайым теңдеулерді шешу тәсілдері үйретіледі, бар бөлігі-құрамында әріп бар өрнек, ал екінші бөлігі санды өрнек болатын теңдеулемен таныстыру бағытынды жұмыстар жүргізіледі оқушылар теңдеуді мысалдардың дербес түрі, яғни "құрамында әрігшен таңбаланған белгісіз болатын теңдік" ретінде, ал теңдеуді шешуді-"оны тура санды тендікке айналдыратын әріптің сәйкес мәнін табу" деп түсінуіне жету кезделеді. Осының бәрі анықтамалар бойынша енгізілмей. қарапайым жаттығулар мен практикалық жұмыстарға және қажетті өрнекіліктерге сүйену арқылы жүзеге асырылады қосу мен көбейту таблицаларын және азайту мен бөлудің сәйкес жағдайларын оқып үйрену барысында ⁯+=7, ⁯-3=5, 8-□=2, 0-3=12, ⁯:5=4, 24: ⁯ =8 сияқты жаттығулар қарастырылады. □ белгі-белгісіздің шартты түрде таңбалануы. Қарастырылған жаттығудағы, іздеп отырған санды табудағы іс-әрекет ілгерід тендеуді шешу тәсілінің негізіне алынады. Мысалы, 0 -ден бастап біртіндеп сандарға 2-ні қоса отырып, 7-нің шығатынына, не шықпайтынына көз жеткіземіз 0+2, 1+2... 6+2, 7+2 т.с.с. мысалдар ауызша айтылып, тек қана бір жағдайда 5+2=7 тура санды теңдіктің шығатынына оқушылар назары аударылады. Міне, теңцеу терминін енгізу үшін осындай мысалдарды қарастыра отырып, белгісіздің □ сияқты таңбалануының орнына әріптер пайдаланатынын хабарлау және сонда шығатын х+2=7, х-3=5, 8-х=2, х·3=12, х:5=4, 24· х=8 сияқты мысалдардың тендеулер деп аталатынын айту жеткілікті. Оқушылар оқулықтағы жаттығулар ішінен теңдеулерді ажырата білсе, теңдеу жөнінде дұрыс түсінік қалыптасты деуге болады.
Теңдеуді шешудің алғаш енгізілетін тәсілі-"тандап (іріктеп) алу" ол теңдеудегі сандық деректер таблицалық жағдайлармен байланысты болғанда мейлінше тиімді. Мысалы, х:5=4 теңдеуді шешу үшін 5-ке бөлудің таблицалық жағдайлары еске түсіріледі, яғни 5, 10, 20, 25, 30, 35 т.с. 5-ке бөлінеді соның ішінде оқушылар бөлгенде 4 шығатынына оқушылар назар аударады. Теңдеуді шешу барысында іздеп отырған сан іріктеліп алынғанда нәтижелер ауызша тексеріліп, ақтық нәтиже анықталғанға дейін ол жалғастырыла беретіндіктен, тендеу шешуінің дұрысгығын арнайы тексеріп және оны жазудың қажеті болмайды. Бұл тәсіл теңдеуді шешу дағдыларын қалыптастырудың бастама кезінде ең үйлесімді және барынша тиімді. Бірақ, ілгеріде теңдеуді шешудің одан да, тиімді тәсілдері енгізіледі ол-берілген және іздеп отырған сандар арасындағы өзара байланысқа негізделген арифметикалық амалдардың белгісіз компоненттерін табу. Мысалы, х+3=19 теңдеуін шешу керек болсын. Оқушылар өздеріне белгілі тәсіл "тандап алуды" пайдаланады, яғни 0-ден 7-ге дейін сандарды тексеріп көреді. Бұған біраз уақыт кететіне олардың назары аударылады. Енді осы теңдеуді шешудің тиімді тәсілін іздестірейін. Теңдіктін сол бөлігінде х пен 3-тің қосындысы, ао оң бөлігінде 19. Демек 19 қосынды, х пен 3 қосылғыштар. Ал қосындыдан қосылғыштардың бірін алсақ, екіншісі шығады. х=19-3. Әрі қарай нәтиже есептеледі. Сәйкес тендеудің шешуін жазудың үлгісі беріледі.[16]
х+3=19- берілген тендеу
х=19-3 - белгісіз қосылғыш
х=16 - нәтиже есептеледі
16+3=19
19=19 - теңдеудің шешуі тексеріледі
Осындай жазу үлгісін бірлі-жарым мысалдарды оқушылардан талап ету керек. Сонда ғана оқушылар тендеу шешуін тексерудің мағынасын және мәнді ерекшелігін саналы түсінетін болады.
Бастауыш сыныптарда а+-х=в, х+-а=в түріндегі қарапайым теңдеулерді (х-белгісіз сан, а және в-белгілі сандар) шешу былайша жүзеге асырылады.
-тендеу құрамына енетін өрнекті талдау арқылы тендеудің сол бөлігінде амалды (қосу не азайту) қандай сандармен орындағанда оның оң бөлігінде шығатын нәтиженің не екені (қосынды не айырма) анықталады
-қосудың ауыстырымдылық заңын немесе азайту амалының мән-мағынасын құрамында әріп бар теңдікке қолданып, а+х=в, х-а=в, а-х=в түріндегі теңдеулерді х+а=в түріне келтіру немесе х=а+в бірден шешу
-тура тендіктің екі бөлігінен де бірдей санды азайтқанда, тағы да тура теңдік: шығатынын ескеріп тендеудегі белгісізді даралау
-өрнекті ықшамдау және есептеулерді орындау
-теңдеудің шешуін тауып, оны тексеру.
Бастауыш буында қарапайым теңдеулерді, сондай-ақ амалдың қандай да бір компонентте немесе нәтижесі санды өрнектер болып келетін теңдеулерді х-8= 12+5, 2-х=32:4, х+3-8=45 т.с.с. қарастырылып оларды шешу тәсілдерін үйрету керек те ол осындай теңдеулер құруға келтіретін, тексті арифметикалық есептер шығарумен қорытындылануы тиіс. Мысалы: "ойлаған санға 3-ті 7 саны шықты. Ойлаған санымыз қандай сан?" немесе "Ойлаған сан мен 2-нің айырмасы 6-ға тең. Ойлаған санды тап".[10]
5+х=7
х+3=5
х-3=6
9-х=7
түгіндегі теңдеулермен оқушылар 2-ші сыныпта танысады. Мұндай түрдегі теңдеулерді құра білу және шеше білудің білік, дағдылары қалыптасқанда ғана оқушылар мазмұнды есептерді тендеу құру арқылы шығара алатын болады.[17]
Мазмұнды есептерді теңдеу құру арқылы шығаруға үйрету мынадай есептерден бастаған жөн: "бірінші қосылғыш - 25, екінші қосылғыш -белгісіз, қосынды - 42. Белгісіз қосылғышты табу керек".
Есеп мазмұны бойынша теңдеу құрамыз: 25+х=42.
Мұндай теңдеу оқушыларға таныс тендеу болғандықтан оқушылар оны оңай шеше алады.
Дәл осылайша жай есептерді арифметикалық амалдардың компонеттерін негізделетінін оқушыларға ұғындырған соң кесте түрінде берілген жай есептерді шығару арифметикалық амалдардың компонеттерін табуға негізделетінін оқушыларға ұғындырған соң кесте түрінде берілген жай есептерді оқи білуге және шығаруға, үйретуге болады. Осы мақсатта мынадай есепті қарастырған жөн:

Азайғыш
Х
5
10
х
10
Азайтқыш
5
Х
8
2
х
Айырма
8
4
х
7
5

Оқушылар есепті оқиды: "Азайғыш-белгісіз, азайтқыш-5, айырма-8. Азайғышты табу керек?"
Оқушылар есеп мәтіні бойынша теңдеу құрады: х-5=8
Бұл теңдеуді шешу тәсілімен оқушылар таныс, сондықтан оны шешу арқылы кесте түрінде берілген есепті шығаруды оқушылар оңай меңгереді. Бұдан соң сюжеттік есептерді шығаруға көшуге болады. Мысалы мынадай есеп ұсынылады:
"Ерланның бірнеше дәптері бар еді, ол тағы 4-ін сатырап алды, сонда Ерланда 12 дәптер болды. Ерланда қанша дәптер болған еді?"
Есептің шартын талдау кезеңінде "бірнеше" деген сөз "белгісіз" дегенді білдіретіндігі анықталады, яғни х әрпімен белгіленеді де, есептің шарты қысқаша жазылады:
Болды- х (1) қосылғыш
Сатып алды-4 (2 қосылғыш)
Барлығы-12 (қосынды)
Есептің шарты түрлендіріп оқылады:
"Бірінші қосылғыш - х, екінші қосылғыш-4, қосынды-12. Бірінші қосылғышты табу керек?" Теңдеу құрылады: х+4=12, бұл теңдеу белгісіз қосылғышты табу ережесіне сүйеніп, оңай шешіледі. Осылайша берлілген сюжеттік есептің шешуі табылады.
Мазмұнды есепгердің шарты бойынша сан өрнектерін, әсіресе айнымалысы бар өрнектерді құра білу-есептерді теңдеу құру арқылы шығаруға үйрену жолындағы ең бір негізгі мәселе. Бастауыш сыныпта оқушылар сәл күрделілеу 17+х=28-5, (20+6)-х=15 және т.б. Осыған ұқсас осындай тендеулермен танысып, оларды шеше білуге үйренеді. Мұндай теңдеулермен танысу есептің қысқаша жазылуында қолданылатын амал компонеттері көрсетілген сюжеттік есептер шығарумен байланысты да қарастырылады 15+х=32-14 түріндегі тендеумен және оны шешу жолымен таныстыруда мынадай есепті ұсынуга болады: "Бірінші қосылғыш-15, екінші қосылғыш-белгісіз, ал қосынды 32 мен 14 сандарының айырмасы. Белгісіз қосылғышты табу керек? [9]
Есепті шығару үшін белгісіз қосылғышты х деп белгілеп, есеп мәтіні бойынша теңдеу құрылады: 15+х=32-14
Мұғалім 15 пен х сандарының қосындысы санмен емес, 32 мен 14 сандарының айырмасы арқылы өрнектеліп тұрғандығына оқушылардың назарын аударады да, айырманың мәнін есептеу керек екенін айтады. Оқушылар есептеп, айырманың мәні 18-ге тең екенін табады. Мұғалім 32 мен 14 сандарының айырмасының орнына оның мәнін жазу керек екенін айтады. Сонда 15+х=18 түріндегі жаңа тендеу алынады. Ал мұндай теңдеу оқушыларға бұрыннан таныс болғандықтан, оқушылар теңдеуді әрі қарай өздері шеше алады.
Мұғалім тендеудің шешімін тексерудің жазулуының ерекшелігін көрсетеді. Жалпы, теңдеуді шешудің жазылуы төмендегі болады.
15+х=32-14
15+х=18
х=18-15
х=3
15+3=32-14
18=18
Мұғалім теңдеуді шешу барысындағы түрлендірулер мен теңдеудің шешімін тексеруге оқушылардың назарын қайталап аударады, содан кейін 28-х=12+5, х-6=7+8, т.с.с. тендеулерінің шешімін табу арқылы теңдеуді шешу тәсілі, дағдылары бекініледі. Дәл осы сияқты оқушыларды (20+6)-х=15 тендеуімен және оны шешу әдісімен таныстыруға болады. Ол үшін мынадай есеп ұсынуға болады:
"Азайғыш-20 және 6 сандарының қосындысы, азайтқыш белгісіз, айырма-15. Азайғышты табу керек".
Есептің мәтіні бойынша тендеу құрылыда: (20+6)-х=15, мұнда мұғалім "ыңғайлылық" үшін алдымен 20+6 қосындысын есептеу арқылы азайғыштың орнына 26 санын қоюды ұсынады Сонда тендеу 26-х=15 түрінде жазылады, одан әрі теңдеудегі іс-әрекеттер жоғарьщағы есепті шығару мен бірдей болады.[18]
Оқушылар көрсетілген түрдегі тендеулердің шешімін табуды үйренген соң, меңгерген білік, дағдыларын кесте түрінде берілген есептерді шығаруда қолдана білуге жаттықтырылады. Мұндай есептерді шығаруға үйрету әдістемесі көбіне өрнек құруғу берілген есептерді шығаруға үйрету әдістемесіне ұқсас боп келеді. Мысалы, мынадай есеп берілсін:
Төменгі кестедегі есепті оқы және шығар:
қосылғыш х 17-9
қосылғыш 8 х
қосынды 3·5 20
Бұл кестеде екі есеп бар:
1) Бірінші қосылғыш белгісіз, екінші қосылғыш-8, қосынды - (3 :: 5) өрнегі. Белгісіз қосылғышты тап.
2) Бірінші қосылғыш-17 мен 9 сандарының айырмасы, екінші қосылғыш белгісіз, қосынды - 20. Екінші қосылғышты табу керек.
Есептің осындай жеңілдетілген түрде берілуі бойынша немесе кесте бойынша да бірден есептерге шешімдері табылады.
IV сыныпта оқушылар тендеудің х-12+36=60, 560:х=57-37 (х-380):50=2000, 10 :: х=8 :: 25 және т.б. түрдегі жаңа түрлерімен танысады. Сол кезенде оқушылар сюжеттік есептерді теңдеу құру арқылы шығаруға үйретіледі. Мысалы: "Әйгерімнің сурет альбомның 20 беті бар, әр бетте 3 суреттен салынған. Әйгерім тағы бірнеше суретті альбомға желімдеді, сонда альбомда 78 сурет болды. Әйгерім альбомға неше сурет желімдеген?". Мұғалімнің көмегімен оқушылар есепте ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.