Көмекші мектеп оқушыларына жай бөлшектерді меңгерту жүйесі: ортақ бөлімге келтіру және қосу алгоритмі


М. Х. Дулати атындағы Тараз өңірлік университеті
Педагогика жоғары мектебі
КУРСТЫҚ ЖҰМЫС
Тақырыбы:Жай бөлшектерді меңгеру жүйесі. Жай бөлшектерден бірдей мәнді алу және қосу алгоритмі.
Орындаған:Толымбек Гүлжауһар
Тобы:Деф 18/1
Қабылдаған:
2020жыл
МАЗМҰНЫ
КІРІСПЕ . . . 2.
I. Бөлім. Көмекші мектеп оқушыларында «үлес», «бөлшек» - деген ұғымдарды калыптастыру жұмысы.
1. 1 Бөлшектердің құрылуы, «бөлінді», «бөлінгіш» - деген түсініктер
1. 2 Көмекші мектеп бағдарламасында жәй бөлшектерді оқытудың орналасуы, маңызы.
II. Бөлім. Ақыл-ойы кем оқушылардың ондық белшектерді меңгеруде , оның себептері.
2. 1 Ондық бөлшектерді салыстыру, түрлендіру және олармен арифметикалык амалдарды орындауды үйрету әдістемесі.
2. 2 Мүмкіндігі шектеулі балдарға жай бөлшектермен қосу, алу арифметикалық амалдарды орындауды және оларды тұтас санға көбейту, бөлуді үйрету әдістемесі.
ҚОРЫТЫНДЫ . . . 29.
ӘДЕБИЕТТЕР ТІЗІМІ . . . 30.
КІРІСПЕ
Курстық жұмыстың өзектілігі: Жай бөлшектерді оқыту ақыл-есі кем оқушылар үшін сандар туралы білімдерін кеңейтеді. Оқушылар натурал сандардан басқа басқа бөлшектер бар екенін, олардың ерекше қасиеттері бар екенін, ал бөлшектерді білгенде натурал сандар сияқты қосуға, азайтуға, көбейтуге және бөлуге болатындығын біледі. Олар бүтін сандар сияқты бірдей заңға бағынады. Мұның бәрі бақылауды, зейінді, логикалық ойлауды, себеп-салдар байланыстарын таба білу қабілетін және т. б. жақсы әсер етеді.
Бөлшектерді зерттеу оқушылардың сөздік қорын жаңа сөздермен байыта отырып, сөйлеуді дамытуға оң әсерін тигізеді: тең бөліктерге бөлу, тең жартыларға, бөлшектерге, бөлшектерге, аралас сандарға, бөлшектерге, бөлшектерге, қысқартуларға және т. б.
Өмірлік тәжірибе интеллектуалды кемістігі бар оқушылар үшін бөлшектерді игеруде маңызды.
Мектеп қабырғасында оқушылар жай бөлшектер сияқты бөлшектермен кездеседі. Бөлшектерді білмеу арнайы мектеп түлектеріне мамандықтарды игеруді қиындатады, бағдарлауда қиындықтар туғызады.
Оқушыларға сыныптағы бөлшектердің қасиеттері туралы негізгі түсініктер мен білімдерді сіңіру үшін мұғалімге көрнекі құралдарды, дидактикалық материалдарды көп қолдану қажет.
Қарапайым бөлшектерді үйрету үшін қандай көрнекі құралдар мен дидактикалық материалдарды қолдану керек?
Бұл келесі материалдар:
- тең бөліктерге бөлуге болатын заттар: алма, торт, джем, қарбыз және т. с. с. - осы заттарды бөлген кезде бөліктер болады, яғни олар бүтіннен ерекшеленеді - бұл алманың жартысы, төрттен бірі;
- тең бөліктерге бөлінген заттардың немесе шарлардың макеті;
- тең бөліктерге бөлінген картон, қағаз, фанер дөңгелектері;
- тең бөліктерге бөлінген квадраттар, үшбұрыштар, сызықшалар;
- бірліктерге бөлінген сынып шоттары;
- тең бөліктерге бөлінген заттар, шеңберлер, квадраттар, үшбұрыштар, кесінділер бейнеленген кестелер;
- бөлшектері мен бөлшектері көрсетілген кестелер;
- қарапайым бөлшектерді бір-бірімен салыстыру, суреттер кестесін бірліктермен салыстыру.
Ақыл-есі кем балалар қарапайым бөлшектерді біліп, оларды оңай түсінуі үшін мұғалім еңбекқор және білімді болуы керек.
Курстық жұмыстың мақсаты: Жай бөлшектерді қосу және азайту ережелерімен таныстыру, осы ережелер негізінде жай бөлшектерді қосу және азайту дағдыларын қалыптастыру. Мүмкіндігі шектеулі балдардың ой-өрісін дамыта отырып, алған білімдерін есептер шығаруда қолдана білуге үйрету. . , ұқыптылыққа, ұйымшылдыққа, , еңбекке тәрбиелеу.
Курстық ұмыстың міндеттері:
-Үлес және бөлшек ұғымдары туралы түсінік қалыптастыру;
-Арнай мектептерде жай бөлшек және әртүрлі бөлшектерді қосу мен азайтудың алгоритмін меңгеру әдістемесі;
-Арнайы мектептерде жай бөлшектерді көбейту және бөлу әдістемесі;
-Жай бөлшектерге байланысты мәтіндік және қарапайм есептерді шешу.
-Мүмкіндігі шектеулі балалардың оңдық бөлшекті меңгеруң және олардың қасиеттерімен заңдары.
Курстық жұмыстың зерттеу обьектісі: Көмекші мектеп оқушыларыңда жай бөлшек пен оның қасиеттерің қалыптастыру мәселелері.
Курстық жұмыстың зерттеу пәні: Көмекші мектептерде жай бөлшектерді меңгеру жүйесі мен қосу, алу алгоритім ұғымдарын қалыптастырудың тиімді жолдарың анықтау.
Курстық жұмыстың зерттеу әдістері: Зерттеу тақырыбына қатысты математикалық әдістемелік оқулықтарын, топтамалар мен кешендерді талдау.
Курстық жұмыстың зерттеу көздері: Зерттеу мәселесі бойынша математика, педагогика ғалымдарының әлеуметтанушылардың психолгтардың еңбектері; « Математика». Көмекші мектепке арналған байқау бағдарламасы; Перова М. Н. «методика преподования математики по вспомогательном школе». Сүлейменова Р. А., Елисеева И. Г., Карипжанова Ш. Ж. Б19 Математика. Арнайы мектепке арналған байқау бағдарламасы. Осы орайда білім беруді дамыту тұжырымдамасының педогигикалық және жас ерекшелігі психологиясы теориялары, ұлттық-тәлім тәрбие туралы ғылыми зерттеулер мен теориялық әдебиеттері негзіздеріне сүйеніп жасалған.
Курстық жұмыстың құрылымы: Курстық жұмыс кіріспеден, екі бөлімнен, қортындыдан және пайдаланылған әдебиеттер тізімінен тұрады .
Кіріспе бөлімінде осы тақырыптың көкейкестілігі, көмекші мектепте математикалық жай бөлшектер мен жай бөлшектерді қосу, алу алгоритім ұғымдарын үйрету мәселелері және оқу тәрбие процесінің бірізділігі, оны зерттеуге ат салысқан ғалымдардың еңбектерінің құндылығы қарастырылады. Зерттеу жұмысының ғылыми аппараты, мақсаты, міндеттері әдістері обьектісі мен пәні көрсетіледі.
«Көмекші мектеп оқушыларында «үлес», «бөлшек» - деген ұғымдарды калыптастыру жұмысы» деп аталатын бөлімде үлес және бөлшек ұғымдарын туралы түсінік қалыптастыр, жай бөлшектерді меңгеру және арнайы мектеп сыныптарда математикасында жай бөлшекпен үлес ұғымдарын кеңейтіп оқытудың маңызы қарастырылады.
«Ақыл-ойы кем оқушылардың ондық белшектерді меңгеруде , оның себептері. » деп аталатын бөлімде ондық бөлшектерді салыстыру, түрлендіру және жай бөлшектерді қосу, алу арифметикалық амалдарын ерекшеліктері мен оқту жолдары мен әдіс-тәсілдер қарастырылады.
I. Бөлім. Көмекші мектеп оқушыларында «үлес», «бөлшек» - деген ұғымдарды калыптастыру жұмысы.
1. 1 Бөлшектердің құрылуы, «бөлінді», «бөлінгіш» - деген түсініктер
Зияты бұзылған оқушылардың бөліктерді, жай бөлшектерді және тұтас бөліктерге бөлу туралы білімдерінің бір бөлігі өмірде қолдануға және танысуға болады.
Ойын барысында іс жүзінде олар бәрін тең бөліктерге бөлуге тап болады, мысалы: тақтаны екіге тең бөлікке кесу, лентаны жартыға немесе төрттен кесу, алма, нан, пирогты 2 немесе 4 тең бөлікке кесу, кәмпитті екіге бөлу, матаны екіге бөлу екі, үш, төртке бөлу және т. б.
Бірақ оқушылар бөліктерді оқи отырып, бөлшектер санының жаңа қасиеттері мен сапасы туралы біледі. Олар натурал сандардан өте ерекшеленеді: аты, жазуы және т. б.
Бүтін сандарды тең бөліктерге бөлу арқылы бөліктер туралы алғашқы түсінікті арнайы мектеп оқушылары 5-сыныпта меңгеруі керек.
Тұтасты тең бөліктерге бөлмес бұрын, оқушыларға белгілі бір жағдай жасау керек. Мысалы, мұғалім оқушыға алма беріп, «Сізде бір ғана алма бар. Сіздің досыңыз сізге келді, сіз онымен алманы бөліскіңіз келеді. Сіз бұл жағдайда не істер едіңіз? «Студент:« Алманы екіге бөлу керек »деп жауап береді. Мұғалім: «Екіге бөлу дегеніміз екі тең бөлікке бөлу деген сөз» деп түсіндіреді.
Содан кейін оқушылар бәрін тең екі бөлікке бөлуі керек (кәмпиттер, алма, нан, лента, қағаз және т. б. ) . Барлығын бірдей екі бөлікке бөліңіз, кесу, майыстыру, сындыру және т. с. с әрекеттерді орындауға болады.
Оқушылар бүтін санды екі тең бөлікке бөлгенде, олардың екінші бөлігі немесе жартысы бірдей екеніне және әртүрлі натурал сандардың бөліктері немесе жартысы сәйкес келмейтіндігіне көз жеткізуі керек. Мұны істеу үшін, мысалы, мұғалім бір оқушыға үлкен көк шеңбер, ал екінші оқушыға кішігірім қызыл шеңбер беріп, осы шеңберлерді екі тең бөлікке бөлуді сұрайды. Содан кейін ол сұрақтар қоя бастайды: «Неше жарты шықты? Бір шеңбердің жартысы екінші шеңберге тең бе? Әр шеңбердің жартысы тең екенін көрсетіңіз? Көк және қызыл шеңберлердің жартысын салыстырыңыз? Шеңбердің қай жартысы үлкен? Не үшін?»
Оқушылар бөлік тұтасқа бағынышты екенін түсінуі керек. Егер зат тең бөліктерге бөлінсе, онда бұл бөліктер тең, бірақ әр түрлі заттардың бір-біріне тең емес бөліктері, егер олар бірдей бөлінсе де. Сондықтан, егер заттар тең болмаса, онда олардың бөліктері тең болмайды, яғни олар сәйкес келмейді.
Квартеттер, октеттер және басқа бөліктерді қолданып көріңіз.
Бұл бөліктермен танысу кезінде үшбұрыштарды, тең бүйірлі үшбұрыштарды, түзулерді, кесінділерді қолдану қажет.
Мүмкіндігінше сіз студенттердің барлық жұмыс түрлерін дәптерге жазуыңыз керек: бөліктерді желімдеу, сурет салу аймақтары, сызықтар салу, бояу. Қорытындылай келе, оқушылар тұтасты екіге, үшке, беске, онға және т. с. с. -ға бөлгенде жалпылауды қалыптастырады. Егер біз оны тең бөліктерге бөліп, содан кейін қажет болған жағдайда кез-келген бөлігін алсақ, онда біз үшінші, бесінші, оннан бірі және т. б. бөлшектер.
Одан кейін студенттер егжей-тегжейлі қарастырады. Егер біз бүтіннің бір немесе бірнеше бөлігін алсақ, онда біз оның бір бөлігін аламыз. Бөлшектер екі санмен оқылады. Бірінші сан бөліктердің санын, ал екіншісі элементтің қанша бөлікке бөлінетінін көрсетеді. Мысалы, үш тоқсан. Оқушыларға мәліметтерді қалай жазу керектігін көрсету керек. Мәліметтер екі санмен көрсетіледі, олардың бірі көлденең сызықтың үстінде, ал екіншісі төменде жазылған. Мысалы
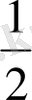 - екіден бір немесе жарты;
- екіден бір немесе жарты;
 - үштен екі.
- үштен екі.
Жолдың астындағы сан бүтіннің қанша тең бөлікке ие екенін көрсетеді, оны бөлшек бөлік деп атайды. Түзудің үстіндегі сан осы бөлшектердің қанша алынғанын көрсетеді, оны бөлшек заряд деп атайды.
Оқушылардың егжей-тегжейін, оқу мен жазуды нығайту үшін жаттығулар жүргізілуі керек.
Оқытудың бұл кезеңінде оқушыларға өлшеу кезінде сандарды бөлшек түрінде жазуға болатындығын көрсету керек. Бұл білімді ұзындықты өлшеу мысалдарымен түсіндіруге болады.
Мысалы, қаламды немесе сызықты өлшеу кезінде 10 см немесе 1 дюйм деп айтуға болады. Еске түсірейік 1метрде 10дм бар (метрді дециметрмен бөлгенін көрсету керек) . Содан кейін 1дм =
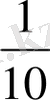 м немесе 10см=
м немесе 10см=
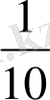 м; 5дм =50см=
м; 5дм =50см=
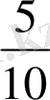 м; 50см =
м; 50см =
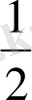 м (егер метрді ортасынан бөлсек,
м (егер метрді ортасынан бөлсек,
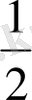 м шығады) . Егер 1 м-ді 4 бірдей бөлікке бөлсек, онда
м шығады) . Егер 1 м-ді 4 бірдей бөлікке бөлсек, онда
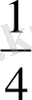 м шығады: 20см =
м шығады: 20см =
 м т. б.
м т. б.
Оқушылар бөліктерді тек ұзындығын өлшеу үшін ғана емес, сонымен қатар уақытты, салмақты және сұйықтықты өлшеу үшін қолдана алады.
Зияты бұзылған студенттер барлық сандардың бүтінге бөлінбейтіндігіне көз жеткізді. Кіші бүтін санды үлкен бүтін санға бөлуге болмайды. Күнделікті өмірде 3алма5 адамға, 2 тоқаш3теңбөліккежәнет. б. Оқушылардың тәжірибесін қолдана отырып, бүтін санды бүтін санға бөлгенде бөлшек болатынын көрсете аламыз.
Жай бөлшекті алу
. Жай бөлшекті бүтінге бөлу арқылы қалай алуға болатындығын түсіндіру үшін практикалық мазмұндағы есептерді шығару керек. Мысалы, 3 балаға 2 кәмпит беру керек. Біз мұны қалай жасаймыз? 1 кәмпит алыңыз және оны 3 тең бөлікке бөліңіз. Әрқайсысы
 бөлігіналады. Содан кейін екінші кәмпитті алып, оны да 3 бірдей бөлікке бөлеміз. Әрқайсысы тағы да
бөлігіналады. Содан кейін екінші кәмпитті алып, оны да 3 бірдей бөлікке бөлеміз. Әрқайсысы тағы да
 бөлігін алады. Әр бала қаншадан алды? Әр бала кәмпиттің
бөлігін алады. Әр бала қаншадан алды? Әр бала кәмпиттің
 бөлігін алды (оқушылар бұны көру керек) . Былай жазайық: 2:3=
бөлігін алды (оқушылар бұны көру керек) . Былай жазайық: 2:3=
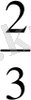 .
.
Бөлшектерді салыстыруды оқушыларға білімдерін және тәжірибелерін пайдалана отырып, тұтасты тең бөліктерге бөлу арқылы бөлікті алу үшін түсіндіруге болады. Алманы алып 4 бірдей бөлікке бөлеміз. Алманың
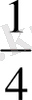 және
және
 бөліктерін салыстырамыз. Қайсысы үлкен
бөліктерін салыстырамыз. Қайсысы үлкен
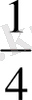 па, әлде
па, әлде
 па? Оқушылар көру арқылы
па? Оқушылар көру арқылы
 >
>
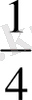 екеніне көз жеткізеді. Мұғалім оқушылардың назарын бөлшектің бөлімі мен алымына аударады.
екеніне көз жеткізеді. Мұғалім оқушылардың назарын бөлшектің бөлімі мен алымына аударады.
Содан кейін мұғалім оқушылардан бірдей ақыға әр түрлі сандар қатарын жазуды және оқушылардан осы сызбаларды қағаз сызықтары немесе кесінділер арқылы қалай алғанын көрсетуін сұрайды. Ол алдымен бөліміне аударады (барлық бөліктер бірдей бөлікке ие), содан кейін олардың коллекциясына (әр түрлі коллекциялар) немесе осы кесінділерді сурет салу арқылы салыстыруды ұсынады. Оқушылар қорытындыға келеді: бөлшектері бірдей бөлшектердің заряды неғұрлым көп болса, бөлшек соғұрлым үлкен болады. Соңғы ережені құру үшін қарастырып, салыстыру қажет. .
Ары қарай оқушыларға мынадай тапсырмаларды ұсынуға болады. Келесі бөлшектерді салыстыру:
 ,
,
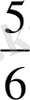 ,
,
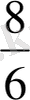 ,
,
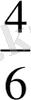 ,
,
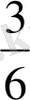 ,
,
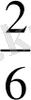 ,
,
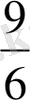 ,
,
 , кішіден үлкенге қарай жазу керек (және керісінше) ; берілген бөлшек қатарынан ең кішісін ата; берілген бөлшек қатарынан 5\6 кіші бөлшектерді ата.
, кішіден үлкенге қарай жазу керек (және керісінше) ; берілген бөлшек қатарынан ең кішісін ата; берілген бөлшек қатарынан 5\6 кіші бөлшектерді ата.
Бұл кезде оқушыларды бөлшектермен және бөлшектермен салыстырады және осы білім негізінде оң және теріс бөлшектер түсіндіріледі. Мысалы, мынадай тапсырманы орындай керек:
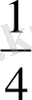 ,
,
 ,
,
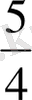 бөлшектердің пайда болуы кесінділермен, сызықтармен, шеңберлермен көрсетілуі керек; сұрақтарға жауап беріңіз: қандай бөлшек кіші, қайсысы тең, қайсысы үлкен.
бөлшектердің пайда болуы кесінділермен, сызықтармен, шеңберлермен көрсетілуі керек; сұрақтарға жауап беріңіз: қандай бөлшек кіші, қайсысы тең, қайсысы үлкен.
Дұрыс және теріс бөлшектер.
Оқушылардың бойында жағымды және жағымсыз бөлшектер туралы идея визуалды және практикалық әрекеттерді қолдану арқылы қалыптасады. Оқушыларға бүкіл шеңберді алып, оны тең бөліктерге бөліп, ширек, содан кейін екі ширек, үш ширек алып, бөліктерді (бөліктерді) бүкіл шеңбермен салыстыру ұсынылады. Қорытындылай келе, студенттер бұл бөлшектердің аз екеніне бірден көз жеткізеді. Бұл салыстыруды басқа иллюстрациялармен жүргізуге болады: квадрат, нүктелік сызық және т. б. Оқушыларға келесі мәліметтер беріледі:
 ,
,
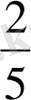 ,
,
 ,
,
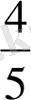 ,
,
 ,
,
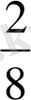 . .
. .
 және т. б. Мұғалім әрдайым оқушылардың назарын берілген бөліктердің бірі үлкен, ал берілген бөліктердің жиынтығы бөлімнен кіші екендігіне аударуы керек. Осы бақылаулардың көпшілігі студенттер практикасында келесі жалпылауға әкеледі: бөлшек - ең кіші бірлік, сондықтан оны тұрақты бөлшек дейміз. Жақсы білім алған студенттер дұрыс бөлшек үшін төлем әрқашан бөлшектен аз болады деп өз бетінше қорытынды жасай алады.
және т. б. Мұғалім әрдайым оқушылардың назарын берілген бөліктердің бірі үлкен, ал берілген бөліктердің жиынтығы бөлімнен кіші екендігіне аударуы керек. Осы бақылаулардың көпшілігі студенттер практикасында келесі жалпылауға әкеледі: бөлшек - ең кіші бірлік, сондықтан оны тұрақты бөлшек дейміз. Жақсы білім алған студенттер дұрыс бөлшек үшін төлем әрқашан бөлшектен аз болады деп өз бетінше қорытынды жасай алады.
Содан кейін оқушылар жағымсыз бөлшектермен танысып, анықтамасын табады. Оларды жоғарыда 4 тең бөлікке бөлінген шеңбердің 4 бөлігін алуға шақырады. . Сол кезде бөлшек шығады
 . Егер барлық 4бөлікті бір-біріне қоссақ, онда шеңбер, яғни бірлік шығады. Осылай оқушылар
. Егер барлық 4бөлікті бір-біріне қоссақ, онда шеңбер, яғни бірлік шығады. Осылай оқушылар
 бөлшегі 1-ге тең екеніне көз жеткізеді.
бөлшегі 1-ге тең екеніне көз жеткізеді.
Содан кейін мұғалім4 тең бөлікке бөлінген2 шеңберді алады және сонымен бірге оқушыларға бірдей көлемдегі 2 тең шеңбер беріп, әрқайсысын 4 тең бөлікке бөледі. Мұғалім көрсетеді, ал оқушылар партаға бір, екі, үш және т. б. қояды. Бұл төрттен бір бөлігін алады. Бір уақытта алынған бөлімді белгілеп, тақта мен бөлімді салыстырады
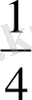 ,
,
 ,
,
 бөлшектері дұрыс бөлшектер. Олар бірден кіші.
бөлшектері дұрыс бөлшектер. Олар бірден кіші.
 бөлшегі 1-ге тең.
бөлшегі 1-ге тең.
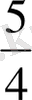 ,
,
 ,
,
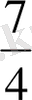 ,
,
 бөлшектері бірден үлкен. Осы бөлшектердің заряды мен бөлінуін өлшемі бойынша салыстыра отырып, оқушылар келесі ережеге келеді: бірге тең немесе одан үлкен бөлшектерді теріс бөлшектер деп атайды. Теріс бөлшек заряд қимасына тең немесе одан үлкен. Содан кейін оң және теріс бөлшектерді ажыратуға арналған жаттығулар бар. Мысалы, келесілер: 1) кесінді сызып, оны 6 тең бөлікке бөліп, алынған бөлшектерді дәптерге жазып, дұрыс бөлшекті көрсет; 2) Берілген бөлімдерге дұрыс және теріс деректерді жазылады:
бөлшектері бірден үлкен. Осы бөлшектердің заряды мен бөлінуін өлшемі бойынша салыстыра отырып, оқушылар келесі ережеге келеді: бірге тең немесе одан үлкен бөлшектерді теріс бөлшектер деп атайды. Теріс бөлшек заряд қимасына тең немесе одан үлкен. Содан кейін оң және теріс бөлшектерді ажыратуға арналған жаттығулар бар. Мысалы, келесілер: 1) кесінді сызып, оны 6 тең бөлікке бөліп, алынған бөлшектерді дәптерге жазып, дұрыс бөлшекті көрсет; 2) Берілген бөлімдерге дұрыс және теріс деректерді жазылады:
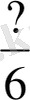 ,
,
 ,
,
 ,
,
 ,
,
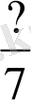 ; 3) берілген алымдар бойынша дұрыс және теріс бөлшектерді жазып шық:
; 3) берілген алымдар бойынша дұрыс және теріс бөлшектерді жазып шық:
 ,
,
 ,
,
 ,
,
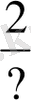 ; 4)
; 4)
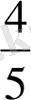 ,
,
 ,
,
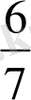 ,
,
 ,
,
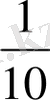 ,
,
 ,
,
 ,
,
 берілген қатарға тек қана жай бөлшектерді жазыңыз, содан кейін 1-ге тең бөлшектерді жазыңыз (тең бөлшектер бірге не деп аталады?) ; 5) 5 оң және 5 жағымсыз бөліктерді жазып, әр бөлік қалай пайда болғанын түсіндіріңіз.
берілген қатарға тек қана жай бөлшектерді жазыңыз, содан кейін 1-ге тең бөлшектерді жазыңыз (тең бөлшектер бірге не деп аталады?) ; 5) 5 оң және 5 жағымсыз бөліктерді жазып, әр бөлік қалай пайда болғанын түсіндіріңіз.
Аралас сандар туралы түсінік көрнекі құралдардың, дидактикалық материалдардың көмегімен, ең бастысы оқушылардың өмірлік тәжірибесі мен практикалық іс-әрекеттерінің көмегімен қалыптасады.
Мысалы, сіз келесі тапсырмаларды ұсына аласыз: «Бір бөлке нан мен жарты нан сатып алды. Нан қанша сатып алынды? «
Аралас сандар мен натурал сандар да бөлшек түрінде жазылады.
Бөлшектің түрленуі. Арнайы мектеп оқушылары бөлшектің келесі түрлерімен танысады: үлкен бөлшек бар бөлшек ұсыну (6-сынып), теріс бөлшектерді бүтін немесе аралас сандармен өрнектеу (6-сынып), сол бөлшектің бөліндісің өрнектеу (7-сынып), аралас сандармен теріс бөлшектер, өрнек (7-сынып) ) .
Теріс бөлшекті бүтін немесе аралас сандар арқылы өрнектеу.
Бұл математиканы келесі 2 шеңберді алып, оларды 4 тең бөлікке бөлуден бастауға болады. Сізге ширектердің санын санауыңыз керек. Онда сіз осы сандардың санын бөлшек түрінде жазуыңыз керек (
 ) . Содан кейін төрттен бір бөліктерді қосу арқылы оқушылар бір бүтін шеңбер шыққанына көздерін жеткізеді:
) . Содан кейін төрттен бір бөліктерді қосу арқылы оқушылар бір бүтін шеңбер шыққанына көздерін жеткізеді:
 =1. Төрт төрттен 1-ге тағыда
=1. Төрт төрттен 1-ге тағыда
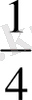 қосылады және оқушылар дәптерлеріне былай деп жазады:
қосылады және оқушылар дәптерлеріне былай деп жазады:
 =1;
=1;
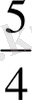 =1
=1
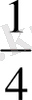 ;
;
 =1
=1
 ;
;
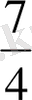 =1
=1
 ;
;
 =2.
=2.
Мұғалім оқушылардың назарын жағымсыз жағдайларға аударады. Түрлендіру нәтижесінде біз бүтін немесе аралас санды аламыз, яғни теріс бөлшекті бүтін немесе аралас санмен өрнектейміз. Қорытынды: Теріс бөлшекті бүтін немесе аралас сан түрінде өрнектеу үшін бөлшектің зарядын бөлшекке бөліп, бүтін сан түрінде жазу керек, қалдықты бөлшекке жазу және бөлшекті сол күйінде қалдыру керек.
Толық немесе аралас сандарды қолданып, теріс бөлшекті қалай өрнектеу керектігін студенттерге түсіндірмес бұрын, оларға бүтін санды бүтін санға, соңына қалдықпен бөлуді ескерту керек.
Жаңа білімді бекіту үшін практикалық мәселелерді шешу өте пайдалы. Мысалы, «вазадағы тоғыз төрттен бір апельсин. Осы тілімдерден қанша толық апельсин ала аласыз? Қанша блок қалды? «
«Қораптың қақпақтарын жасау үшін олар картонның әр бөлігін 16 тең бөлікке бөлді. .
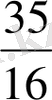 алды. Қанша бүтін картон қағазын кесті?» және т. б.
алды. Қанша бүтін картон қағазын кесті?» және т. б.
Бүтін немесе аралас санды теріс бөлшектер арқылы өрнектеу. Оқушылар осы жаңа біліммен есептер шығару арқылы танысуы керек.
«Ол ұзындығы бірдей квадрат матаның екі бөлігін тең 4 бөлікке кесіп тастады. Мен осы бөліктердің әрқайсысынан сүлгі тіктім. Қанша сүлгі шықты? «
Содан кейін мұғалім оқушыларға келесі тапсырманы ұсынады:
«Бізде осы шеңбердің көлеміне сәйкес тұтас шеңбер және тағы бір жарты шеңбер бар. Барлық шеңберді екі тең бөлікке бөліңіз. Ол неше бөліктен шықты?Жазып алыңдар: 1
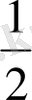 шеңбер болған,
шеңбер болған,
 жеңбер болды, яғни 1
жеңбер болды, яғни 1
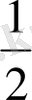 =
=
 болады. »
болады. »
Осы тәжірибеден бірнеше мысал қарастырайық. Бұл мысалдарда студенттерге санды (шығарылғанға дейінгі) (аралас немесе бүтін) және түрлендіруден кейінгі санды салыстыру ұсынылады.
Оқушыларға теріс бөлшектерді пайдаланып бүтін немесе аралас санды қалай өрнектеу керектігін түсіндіру үшін, олар аралас сан мен теріс бөлшектің бөліктерін, заряд қалай пайда болғанын салыстыруға бағытталуы керек. Мысалы:1
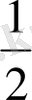 =?, 1=
=?, 1=
 тағы да
тағы да
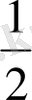 , барлығы
, барлығы
 ; 3
; 3
 =?; 3
=?; 3
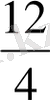 , тағы да
, тағы да
 , барлығы
, барлығы
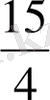 болады. Нәтижесінде келесі ереже құрылады: аралас санды теріс бөлшектермен өрнектеңіз, бөлуді бүтін санға көбейтіңіз және бөлуді өзгеріссіз қалдырыңыз.
болады. Нәтижесінде келесі ереже құрылады: аралас санды теріс бөлшектермен өрнектеңіз, бөлуді бүтін санға көбейтіңіз және бөлуді өзгеріссіз қалдырыңыз.
1. 2 Көмекші мектеп бағдарламасында жәй бөлшектерді оқытудың орналасуы, маңызы.
Бөлшектің негізгі қасиеттері. Арнайы мектеп оқушылары үшін төлем мен бөлуді бір уақытта көбейткенде немесе төмендеткенде бөлшек өзгермейтінін түсіну қиын. Бұл ұғымдар көрнекі құралдар мен дидактикалық материалдардың көмегімен енгізілуі керек, ең бастысы, оқушылар мұғалімнің іс-әрекетін байқап қана қоймай, дидактикалық материалдармен белсенді жұмыс істеп, практикалық әрекеттерді бақылау негізінде белгілі бір қорытындыға келуі керек.
Мысалы, мұғалім бүтін санды алып, оны 2 тең бөлікке бөліп, сұрақ қояды: «Бүтін санды екіге бөлу арқылы не алдық? (2 бөлік) . Тұрыптың
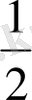 бөлігін көрсетіңдер. Жарты тұрыпты тағы да 2 бірдей бөлікке бөлейік. Не шықты?
бөлігін көрсетіңдер. Жарты тұрыпты тағы да 2 бірдей бөлікке бөлейік. Не шықты?
 Жазып алайық
Жазып алайық
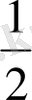 =
=
 . Осы бөлшектердің алымы мен бөлімдерін салыстырайық. Алымы қанша есе көбейді? Бөлімі қанша есе көбейді? Бөлшек өзгерді ме? Не үшін өзгерген жоқ? Бөліктер қандай болады: ірі ме, әлде майда ма? Бөліктің саны көбейіп, азайды ма?»
. Осы бөлшектердің алымы мен бөлімдерін салыстырайық. Алымы қанша есе көбейді? Бөлімі қанша есе көбейді? Бөлшек өзгерді ме? Не үшін өзгерген жоқ? Бөліктер қандай болады: ірі ме, әлде майда ма? Бөліктің саны көбейіп, азайды ма?»
Содан кейін оқушылар шеңберді 2 тең бөлікке бөледі, әр бөлік тағы 2 тең бөлікке бөлінеді, әр ширек тағы 2 тең бөлікке бөлінеді және т. б. сондықтан ол жазады:
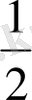 =
=
 =
=
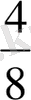 =
=
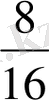 және т. б. Бөлшектің заряды мен бөлігі неше есе көбейтілгенін анықтайды. Элемент өзгерді ме? Содан кейін түзу кесіндісін сызып, оны 3 тең 3, 6, 12 бөліктерге бөліп жаз.
және т. б. Бөлшектің заряды мен бөлігі неше есе көбейтілгенін анықтайды. Элемент өзгерді ме? Содан кейін түзу кесіндісін сызып, оны 3 тең 3, 6, 12 бөліктерге бөліп жаз.
Мысалдар топтамасын көргеннен кейін студенттерден келесі сұраққа жауап беруі сұралады: «Егер біз бөлшек пен бөлшекті бірдей санға көбейтсек, бөлшек өзгере ме?». Оқушылардан мысал сұрау керек.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz