Несие мерзімін және пайыздық мөлшерлеме мөлшерін анықтау

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:

Қазақстан Республикасының Білім және Ғылым министрлігі
А.Байтұрсынов атындағы Қостанай өңірлік университеті
А.Айтмухамбетов атындағы инженерлік-техникалық институты
Физика және математика кафедрасы

Дүйсенбай Арман Қыдырбайұлы

Жай және күрделі проценттер

Курстық жұмыс

Ғылыми жетекшісі: Фазылова А.А.
аға-оқытушы

Қостанай 2020
МАЗМҰНЫ
КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 3
1.Қарапайым пайыздар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..5
0.1. Пайыздар,пайыздық мөлшерлемелер түрлері ... ... ... ... ... ... ... ... ... ... .5
0.2. Қарапайымпайыздық мөлшерлемелер бойынша дисконттау ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..10
0.3. Несие мерзімін және пайыздық мөлшерлеменің шамасын анықтау ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...13
0.4. Тұтынушылық несиедегі пайыздық өсім ... ... ... ... ... ... ... ... ... ... ... ... 15
0.5. Төлемдерді ауыстыру ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 15
0.6. Қаржылық операция контуры ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...17

2.Күрделі пайыздар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 17
2.1Күрделі жылдық пайыздарды есептеу ... ... ... ... ... ... ... ... ... ... ... ... ... .18
2.2Жылына бір рет m пайызының өсуі. Номиналды және тиімді мөлшерлеме ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .20
2.3 Несие мерзімін және пайыздық мөлшерлеме мөлшерін анықтау ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...21
2.4 Валюта айырбастау және пайыздық мөлшерлеме ... ... ... ... ... ... . ... ..23
2.5 Несие мерзімін және пайыздық мөлшерлеме мөлшерін анықтау ... .24
2.6 Валюта айырбастау және пайыздық мөлшерлеме ... ... ... ... ... ... . ... ..25
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..27
Пайдаланылған әдебиеттер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...28

КІРІСПЕ
Бітіруші біліктілік жұмысының таңдалған тақырыбының өзектілігі шарттарды әзірлеу кезеңдерінде қаржы және кредит саласында қаржылық талдаудың сандық әдістерін кеңінен қолдануға негізделген,қаржылық жобалау кезінде, ұзақ мерзімді инвестициялық жобаларды салыстыру және таңдау кезінде, жеке сақтандыруда және т.б.
Қаржылық операцияларды сандық талдау әдістерін білу, олар қаржыгерлердің, бухгалтерлердің, экономистердің, банкирлердің қызметінде пайдаланылады, экономикалық бейіндегі мамандарды даярлау кезінде қажет.
Жұмыстың негізгі мақсаттары-белгілі математикалық формулалар, атап айтқанда қарапайым және күрделі пайыздар негізінде қаржылық есептеулер әдістерін ұсыну; студенттердің болашақ практикалық қызметінде сауатты қолдануы.Санаттар-жинақталған сома, дисконттау, ағымдағы құн, аннуитет және т. б.
Бұл жұмыста шешілетін негізгі міндет-қарапайым және күрделі пайыздарға қатысты оқу материалын оның логикалық тұрғысынан ұсыну жүйелігі.
Мұндай материал құрылымы тереңірек қамтамасыз етеді студенттердің қаржылық есептеу әдістерін игеруі. Шешім нақты тапсырмалар мен алынған нәтижелерді талдау студенттерге дағдыларды дамытуға мүмкіндік береді егізделген экономикалық шешімдер қабылдауда.
Экономикалық тұрғыдан алғанда, күрделі пайыздық әдіс көп негізделген, өйткені ол ақшаны үздіксіз қайта инвестициялау (қайта инвестициялау) мүмкіндігін білдіреді.Алайда, қысқа мерзімді (ұзақтығы бір жылдан аз) қаржылық операциялар үшін қарапайым пайыздық әдіс жиі қолданылады.
Мұның бірнеше себептері бар:
1. Біріншіден, бірнеше ондаған жыл бұрын бұл өте маңызды болды, қарапайым пайыздық әдісті қолдану арқылы есептеулер күрделі пайыздық әдісті қолдану арқылы есептеулерге қарағанда әлдеқайда қарапайым.
2. 2. Екіншіден, шағын пайыздық мөлшерлемелерде (30% шегінде) және аз уақыт аралығында (бір жыл ішінде) қарапайым пайыздық әдіспен алынған нәтижелер күрделі пайыздық әдісті қолдану арқылы алынған нәтижелерге өте жақын (1% айырмашылық).

3
3. Үшіншіден, бір жылдан аз уақыт аралығында қарапайым пайыздық әдіспен табылған қарыз әрқашан күрделі пайыздық әдісті қолдана отырып табылған қарызға қарағанда үлкен болады.
Өйткені ойын ережелері әрдайым несие берушіні талап етеді, бұл жағдайда ол бірінші әдісті таңдайды.
Ескерту: қысқа мерзімді операциялар (ұзақтығы бір жылдан аз) барлық қаржылық операциялардың негізгі бөлігін құрайды. Неліктен? Себебі айына бір рет немесе тоқсанына бір рет (немесе жарты жылда бір рет) -- бұл бір үлкен қаржылық операция емес, бірақ қысқа мерзімді операциялардың үлкен санының жиынтығы (айына, тоқсанына немесе жартыжылдық). Сондықтан Қазақстанда кез-келген несие бойынша пайыздарды есептеу үшін қарапайым пайыз әдісі қолданылады.

4
1. Қарапайым пайыздар
1.1. Пайыздар, пайыздық мөлшерлемелер түрлері
Пайыздық ақша немесе пайыздар бойынша олар кез-келген нысанда қарызға ақша беруден түсетін кірістің абсолютті мөлшерін түсінеді: несие беру, тауарды несиеге сату, ақшаны депозиттік шотқа орналастыру, вексельді есепке алу, жинақ сертификатын немесе облигацияны сатып алу және т. б. Пайыздық мөлшерлеме деп табыстың салыстырмалы шамасы түсініледі.Тіркелген уақыт аралығы-кірістің (пайыздық ақшаның) қарыз сомасы. Ол ондық немесе жай бөлшек немесе В түрінде пайызбен өлшенеді. Есептеулерді орындау кезінде пайыздық мөлшерлемелер әдетте ондық бөлшектермен өлшенеді.Қаржылық талдауда пайыздық мөлшерлеме өлшеуіш ретінде қолданылады.Қарамастан кез келген қаржылық, кредиттік, инвестициялық немесе коммерциялық-шаруашылық қызметтің кірістілік (тиімділік) дәрежесі ақшаны тікелей инвестициялау фактісі орын алды ма, жоқ па қаражат және олардың өсу процесі бақылайды.Пайыздық мөлшерлеме белгіленген уақыт аралығы есептеу кезеңі деп аталады. Мұндай кезең ретінде жыл, жарты жыл, тоқсан, ай немесе тіпті күн қабылданады. Көбінесе іс жүзінде олар жылдық мөлшерлемелермен айналысады.Кредитор мен қарыз алушы арасындағы уағдаластыққа сәйкес пайыздар олардың есептелуіне қарай төленеді немесе негізгі сомаға қосылады (пайыздарды капиталдандыру). Уақыт өте келе ақша сомасын ұлғайту процесі пайыздардың қосылуына байланысты бұл өсу немесе өсу деп аталады сомасы. Бұл жағдайда пайыздық мөлшерлемелер өсу ставкалары деп аталады.
Дисконттау (қысқарту) кезінде болашаққа қатысты ақша сомасы тиісті дисконт (жеңілдік) шамасына азайтылады. Тиісінше, олар жеңілдік немесе есеп ставкаларын қолданады. Қаржы әдебиетінде өсім ставкасы бойынша алынған пайыздар,әдетте декурсивті, есеп ставкасы бойынша -- антиспативті деп аталады.Көптеген жағдайларда декурсивті пайыздар жай пайыздар деп аталады. Қарапайым пайыздарды есептеу үшін тұрақты есептеу базасы қолданылады. Өсудің немесе дисконттаудың алдыңғы кезеңінде алынған сома негіз ретінде қабылданған кезде күрделі пайыздық мөлшерлемелер қолданылады. Бұл жағдайда есептеу базасы дәйекті түрде өзгереді, яғни пайыздар пайыздарға есептеледі.

5
Пайыздық мөлшерлемелер тіркелген (келісімшартта олардың мөлшері көрсетіледі) немесе құбылмалы болуы мүмкін. Соңғы жағдайда ол өзін көрсетпейді мөлшерлеме, ал уақыт өте келе өзгеретін база (базалық мөлшерлеме) және оған үстемеақы мөлшері -- маржа. Маржаның мөлшері бірқатар шарттармен, қарыз алушының қаржылық жағдайымен, несие мерзімімен және т.б. анықталады. Қарызды жүйелі түрде өтеу кезінде екі әдіс болуы мүмкін пайыздарды есептеу. Біріншісіне сәйкес пайыздық мөлшерлеме (қарапайым немесе күрделі) қарыздың нақты сомасына қолданылады. Тұтынушылық несиеде қолданылатын екінші әдіспен қарапайым пайыздар қарыздың бүкіл сомасына оны дәйекті өтеуді ескерместен бірден есептеледі. Практикалық есептеулерде дискретті пайыздар қолданылады, яғни белгіленген уақыт аралықтары үшін есептелген пайыздар (жыл, жартыжылдық және т.б.).
Егер жинақтау немесе дисконттау үздіксіз, шексіз уақыт аралығында жүргізілсе, үздіксіз пайыздар қолданылады. Олар аналитикалық және теориялық қаржылық есептеулерде қолданылады.
1.2 қарапайым пайыздық мөлшерлемелер бойынша өсу
Қарыздың (қарыздың, депозиттің, қарызға берілген немесе инвестицияланған ақшаның басқа түрлерінің) ұлғайтылған сомасы деп оның бастапқы сомасын есептеу мерзімінің соңына есептелген пайыздармен түсіну керек.
Белгілейміз:
I-несиенің бүкіл мерзіміне пайыздар;
P-қарыздың бастапқы сомасы;
S-ұлғайтылған сома, яғни мерзім соңындағы сома;
I-ондық бөлшек түріндегі пайыздардың өсу ставкасы;
n-несие мерзімі.
Барлық мерзімге есептелген пайыздар
I = Pni

6
Ұлғайтылған сома бастапқы сома мен ұлғайтылған пайыздардың сомасын білдіреді:
S P I P Pni P(1 ni) .
Өрнек (1.1) Қарапайым пайыздық формула деп аталады.
Өрнек (1 + ni) қарапайым пайыздарды көбейту мультипликаторы деп аталады, бұл көбейтілген сома түпнұсқадан қанша есе көп екенін көрсетеді.

Қарапайым пайыздар бойынша өсу кестесі 1.2 суретте көрсетілген.

Сур. 1. Қарапайым пайыздар бойынша өсу кестесі
Мысал 1.1. Жинақталған қарыздың пайызы мен сомасын анықтаймыз,
егер несие 500 мың теңгеге тең болса, мерзімі 3 жыл, пайыздар ставка бойынша қарапайым
Жылдық 10% (i = 0,1):
I = 500 5 0,1 = 250 мың теңге,
S = 500 + 250 = 750 мың теңге.
Несие мерзімі бөлшек болған жағдайды қарастырыңыз. N мерзімі мүмкін
бөлшек түрінде ұсыну:
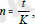
мұндағы t-несие күндерінің саны, К-жылдағы күндер саны немесе пайыздарды есептеудің уақытша базасы.
Пайыздарды есептеу кезінде екі уақытша база қолданылады.
Егер K = 360 күн болса, олар қарапайым немесе коммерциялық пайыздарды алады, ал жылдың нақты ұзақтығын (365, 366 күн) нақты пайыздарды есептейді.

7
Несие күндерінің саны шамамен және нақты күні алынады.
Күндер саны жақындаған кезде айдағы күндер саны 30-ға тең болады
күндер. Несие күндерінің нақты саны несие берілген күн мен оны өтеу күні арасындағы күндер санын есептеу арқылы анықталады.
Екі күн арасындағы күндердің нақты санын Microsoft Excel бағдарламасын немесе күндер кестесін (1-қосымша) пайдаланып есептеуге болады.

Іс жүзінде қарапайым пайыздарды есептеудің үш нұсқасы қолданылады.
1. Несие күндерінің нақты саны бар нақты пайыздар (көрсетілген
365365 немесе АСТАСТ). Ұлыбританиядағы, АҚШ-тағы орталық банктер мен ірі коммерциялық банктер қолданады, дәл нәтиже береді.
2. Несие күндерінің нақты саны бар қарапайым пайыздар (365360 немесе
АСТ360). Кейде банк деп аталатын бұл әдіс коммерциялық банктердің еларалық несие операцияларында, ел ішінде -- Францияда, Бельгияда, Швейцарияда жиі кездеседі. Бұл нақты пайыздарды қолданудан гөрі біршама үлкен нәтиже береді.
3. Несие күндерінің шамамен саны бар қарапайым пайыздар
(360360). Бұл әдіс Германияның коммерциялық банктерінің тәжірибесінде қабылданған,
Швеция, Дания. Ол үлкен дәлдік қажет болмаған кезде қолданылады,
Мысал 1.2.
1 млн теңге көлемінде несие 02.02.03 дейін берілді
15.11.03 жылдық 10% қоса алғанда. Қандай соманы төлеу керек
борышкер қарапайым пайыздарды есептеу кезінде мерзім соңында ма?
Несие күндерінің санын анықтаңыз: дәл -- 285, шамамен -- 282,
02.02.03 және 15.11.03 қоспағанда.
1. Несие күндерінің нақты саны бар нақты пайыздар (365365):
(0,1) 1 078082,19
365
S = 1 000 000 (1 + 285) = тг.
2. Несие күндерінің нақты саны бар қарапайым пайыздар
(360365):
(0,1) 1 079166,7
360
S = 1 000 000 (1 + 285) = тг.
3. Несие күндерінің шамамен саны бар қарапайым пайыздар
(360360):
(0,1) 1078333,3
360
S = 1 000 000 (1 + 282) = тг.

мысалы, аралық есептеулерде.

8

Егер салым бойынша қандай да бір операциялар жүргізілсе: қаражаттың бір бөлігін алу немесе қосымша соманы енгізу болса, онда пайыздар біршама күрделірек есептеледі.

Мысал 1.3.
1 миллион теңге мөлшеріндегі несие. 02.02.03 дейін берілген
15.11.03 жылдық 10% қоса алғанда. Алайда салымшы 25.05.03
оның шотынан 500 мың теңге, ал 02.09.03 қосымша 700 мың теңге төледі.
Есептелген жағдайда шотты жапқан кезде салым сомасы қандай болады
несие күндерінің нақты саны бар қарапайым пайыздар?
Қарастырылып отырған кезең ішінде негізгі салым өзгерді
өз шамасын. 03.02 ішінде.-24.05.03 (110 күн) ол 1 миллион болды
тг., 25.05 ішінде.-01.09.03 (99 күн) ол 500 мың теңгені құрады. және 2.09
14.11.03 (73 күн) - 1200 мың тг.
Пайыздарды екі жолмен есептейміз.
1. Салымның орташа өлшенген қалдығын табамыз
0,8670175
285
1' 110 + 0,5' 99 + 1,2' 73 =млн. тг.
Осы сомадан 285 күн үшін пайыздарды табамыз:
0,1 67698,63
365
I = 8670175 285 = тг.
2. Үш кезеңнің әрқайсысы үшін пайыздарды бөлек есептейміз және
оларды бүктеңіз:
0,1 67698,63
365
0,1 1,2 73
365
0,1 0,5 99
365
I = 1 110 + = теңге.
Көріп отырғаныңыздай, олар бірдей нәтиже алды.
Бұл жағдайда есептелген сома:
S = 1200000 + 67698,63 = 1267698,63 тг.

Кредиттік келісімдерде кейде пайыздық мөлшерлемелер.
Егер бұл қарапайым ставкалар болса, онда мерзім соңында есептелген сома анықталады :
мұнда 1 i -- t кезеңіндегі қарапайым пайыздық мөлшерлеме, 1 n -- тұрақты ставкасы бар кезеңнің ұзақтығы .
Мысал 1.4.
Келісімшарт бірінші жылы пайыздарды 10% есептеуді қарастырады, әрбір келесі жартыжылдықта мөлшерлеме 1% - ға артады.2 жыл ішінде өсу мультипликаторын табыңыз.

9
Тәжірибеде қаражатты қысқа мерзімді депозиттерге инвестициялау кезінде кейде өсімді бірнеше рет жүйелі түрде қайталауға жүгінеді.Берілген жалпы мерзім шегіндегі қарапайым пайыздар бойынша, яғни өсімнің әрбір кезеңінде алынған қаражатты тұрақты немесе ауыспалы мөлшерлемелер көмегімен қайта инвестициялау жүреді.
Барлық мерзім үшін ұлғайтылған сома

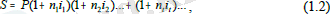
Егер есептеудің аралық мерзімдері мен мөлшерлемелері уақытында өзгермесе, онда бізде
S = p(1+ ni)m ,
мұндағы m-қайта инвестициялау қайталануларының саны.
Мысал 1.5.
1 миллион теңге. 1-ші қаңтарда жылдық 10% - бен айлық депозитке салынады. Егер операция 3 рет қайталанса, есептелген сома қандай?
Егер сіз нақты пайыздарды есептесеңіз( 365365), онда
Қайта инвестициялау кезінде қарапайым пайыздарды есептеу (360360) береді

1.2. Қарапайым пайыздық мөлшерлемелер бойынша дисконттау
Қаржылық тәжірибеде олар көбінесе пайыздарды кері ұлғайту міндетіне тап болады: біраз уақыттан кейін төленуі керек s сомасы үшін N алынған қарыздың мөлшерін анықтау керек Р. есептеу Р бойынша S сомасынан пайыздар алға тартылған кезде де қажет.Яғни,тікелей несие, несие беру кезінде.
Мұндай жағдайларда s сомасы айтылады.Дисконтталады немесе ескеріледі,
Пайыздарды есептеу процесі және олардың ұстап қалу есепке алу деп аталады, ал ұсталған пайыздар, яғни айырмашылық D = S-P - бұл дисконтты немесе жеңілдік.
10
Дисконттау қажеттілігі туындайды.Мысалы, вексельдер мен басқа да қысқа мерзімді міндеттемелерді сатып алу кезінде.
Дисконттауды болашаққа қатысты кез-келген құндық шаманы ертерек уақыт сәтіне анықтау ретінде қарастыруға болады.
Бұл әдіс шығындар көрсеткішін кейбіреулерге келтіру деп аталады,
әдетте бастапқы, уақыт сәті.
Дисконттау арқылы табылған р мәні Қазіргі құн немесе болашақ S төлемінің қазіргі мәні, кейде ағымдағы немесе капиталдандырылған құны деп аталады.
Пайыздық мөлшерлеменің түріне байланысты дисконттаудың екі әдісі қолданылады -- математикалық дисконттау және банктік (коммерциялық) есеп. Бірінші жағдайда өсім ставкасы, екінші жағдайда -- есеп ставкасы қолданылады.
Математикалық дисконттау-бұл жинақталған бастапқы соманы табу. Яғни формуладан
S = P(1+ ni)
Р-табамыз

Осылайша белгіленген Р мәні N жылдан кейін төленетін S сомасының қазіргі мәні болып табылады.
Мысал 1.6.
Шартқа қол қойылғаннан кейін 180 күн өткен соң борышкер 1 млн теңге төлейді. Несие жылдық 10% - бен берілді. Қандай бастапқы база 360 күнге тең болған жағдайда қарыздың жалпы сомасы?
Формула бойынша (1.3) табамыз
Дисконт D=S-P=1-0,95238 = 0,047619 млн тг құрайды.
Бұл көбейткіш бастапқы үлестің қанша екенін көрсетеді қарыздың түпкілікті сомасындағы мөлшері.

11
Банктік есепке алу кезінде банк немесе басқа қаржы мекемесі вексель немесе өзге төлем міндеттемесі бойынша төлем мерзімі басталғанға дейін оны иесінен вексельде көрсетілген сомадан аз бағамен сатып алады, яғни оны жеңілдікпен сатып алады (ескереді).
Вексель мерзімі басталған кезде ақшаны алғаннан кейін банк пайыздық кірісті дисконт түрінде сатады. Вексельдің 12 иесі оны есепке алу арқылы онда көрсетілген мерзімнен бұрын ақша алуға мүмкіндігі бар.
Вексель-бұл борыштық қолхатты білдіретін бағалы қағаз, заң талаптарына сәйкес орындалған, яғни атауы, төлем мерзімі, төлем жасалуға тиіс орны, төлем жасалуға тиіс адамның атауы, вексельдің жасалған күні мен орны, вексель берушінің қолы көрсетілген бланкіде толтырылады. Вексельдің екі негізгі түрі бар - қарапайым және аударылған.
Жай вексель-бұл вексель берушінің міндеттеме мерзімі аяқталғаннан кейін төлеуге сөзсіз ақшалай міндеттемесін куәландыратын құжат вексель иесіне белгілі бір сома беруге міндетті.
Аударым векселі (тратта) - қарыз алушы (вексель беруші) жазып беретін және тікелей төлеушіге (әдетте банкке) көрсетілген мерзімде ақша сомасын үшінші тұлғаға (вексель ұстаушыға) төлеу туралы ерекше ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.