Нетер симметриясын қолдана отырып f(R) модификацияланған гравитация теориясының нақты шешімдерін алу


Қазақстан Республикасының Білім және Ғылым Министрлігі
Л. Н. Гумилев атындағы Еуразия Ұлттық Университететі
Алтынбек Алтынай Мұратбекқызы
«Нетер симметриясы қолданылған
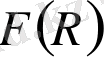 гравитациясы теориясының нақты шешімдерін алу»
гравитациясы теориясының нақты шешімдерін алу»
ДИПЛОМДЫҚ ЖҰМЫС
5B060400 - «Физика» мамандығы
Астана 2017
Қазақстан Республикасының Білім және Ғылым министірлігі
Л. Н. Гумилев атындығы Еуразия ұлттық университеті
«Қорғауға жіберілді»
«Жалпы және теориялық физика кафедрасы»
кафедрасының меңгерушісі
Мырзакулов Р.
ДИПЛОМДЫҚ ЖҰМЫС
Тақырыбы: «Нетер симметриясы қолданылған
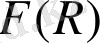 гравитациясы теориясының нақты шешімдерін алу»
гравитациясы теориясының нақты шешімдерін алу»
5В060400 - «Физика» мамандығы бойынша
Орындаған: Фз-41 тобының студенті Алтынбек А. М.
Ғылыми жетекшісі: Мырзакулов Е. М.
PhD, доцент м. а
Астана 2017
Л. Н. Гумилев атындағы Еуразия Ұлттық Университететі
Физика-техникалық факультеті
5В060400 - «Физика» мамандығы
Жалпы және теориялық физика кафедрасы
Бекітемін
Кафедра меңгерушісі
Мырзакулов Р.
«__»20__ж.
Дипломдық жұмысты (жобаны) орындауға
ТАПСЫРМА
Студент Алтынбек Алтынай Мұратбекқызы
4-ші курс, Фз-41 тобы, 5В060400 - «Физика» мамандығы, күндізгі
1. Дипломдық жұмыстың (жобаның) тақырыбы: «Нетер симметриясы қолданылған
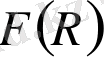 гравитациясы теориясының нақты шешімдерін алу» университет бойынша «__»__20__ж. № ___ бұйрықпен бекітілді.
гравитациясы теориясының нақты шешімдерін алу» университет бойынша «__»__20__ж. № ___ бұйрықпен бекітілді.
2. Студенттің аяқталған жұмысты тапсыру мерзімі «__»__20__ж.
3. Жұмысқа бастапқы мәліметтер (әдеби көздер, зертханалық-өндірістік мәліметтер) Нетер симметриясын қолданып, Ғаламның үдемелі ұлғаюын сипаттайтын
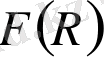 гравитация теориясы нақты шешімдері алынды.
гравитация теориясы нақты шешімдері алынды.
4. Дипломдық жұмыста (жобада) өңдеуге жататын мәселелер тізімі
Бірінші бөлімде, жалы салыстырмалық теориясына кіріспе. Сонымен қатар, космология, күңгірт энергия және күңгірт материя және күңгірт энергияның скаляр өрісте модельдерін қарастырамыз. Екінші бөлімде,
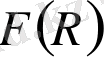 гравитациясы теориясын, метрикалық, Палатиндік, метрикалық аффидік формализмдер қарастырылады. Скаляр-тензорлы космологияда
гравитациясы теориясын, метрикалық, Палатиндік, метрикалық аффидік формализмдер қарастырылады. Скаляр-тензорлы космологияда
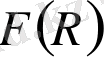 теория гравитациясы қарастырылады. Үшінші бөлімде Нетер симметриясына кіріспе, сонымен қатар, скаляр тензорлы космологияда Нетер симметриясы қолданылған
теория гравитациясы қарастырылады. Үшінші бөлімде Нетер симметриясына кіріспе, сонымен қатар, скаляр тензорлы космологияда Нетер симметриясы қолданылған
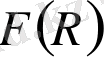 теория гравитациясының нақты шешімдерін алу қарастырылады. Төртінші бөлімде, фермиондық өрісте
теория гравитациясының нақты шешімдерін алу қарастырылады. Төртінші бөлімде, фермиондық өрісте
 -эссенциясы қарастырылады.
-эссенциясы қарастырылады.
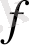 -эссенциясында Нетер симметриясы қолданылған
-эссенциясында Нетер симметриясы қолданылған
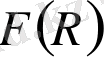 теория гравитациясының нақты шешімдерін алу қарастырылады.
теория гравитациясының нақты шешімдерін алу қарастырылады.
5. Графиктік материалдар тізімі (сызбалар, кестелер, диаграммалар және т. б. )
Нетер симметриясы қолданылған
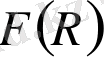 теория гравитациясының нақты шешімдері.
теория гравитациясының нақты шешімдері.
6. Негізгі ұсынылатын әдебиеттер тізімі: Dimitrios Germanis: «General relativity and modified gravity» мақаласы, Miao Li, Xiao-Dong Li, Shuang Wang and Yi Wang: «Dark energy» мақаласы, Varun Sahni: «Dark Matter and Dark Energy» мақаласы, Timothy Clifton, Pedro G. Ferreira, Antonia Padilla, Constantinos Skordis: «Modified gravity and cosmology» мақаласы, Marc Kamionkowski: «Dark energy and dark matter» мақаласы, Paliathanasis A: «Using Noether symmetries to specify
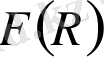 gravity» мақаласы, Darabi F, Asgharinya S: «
gravity» мақаласы, Darabi F, Asgharinya S: «
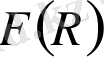 scalar - tensor cosmology by Noether Symmetry мақаласы, Vakili B: «Noether symmetry in
scalar - tensor cosmology by Noether Symmetry мақаласы, Vakili B: «Noether symmetry in
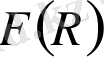
cosmology» мақаласы, Paliathanasis A, Tsamparlis M, Basilakos S: «Scalar-tensor gravity cosmology: Noether symmetries and analytical solutions» мақаласы, Felice D. A, Tsujikawa S: «
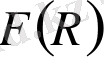 theories», Sotirieu T. P: «
theories», Sotirieu T. P: «
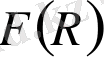 gravity and scalar-tensor theory» мақаласы және т. б мақалалар қарастырылды.
gravity and scalar-tensor theory» мақаласы және т. б мақалалар қарастырылды.
7. Жұмыс бойынша консультация (оларға қатысты жұмыс бөлімдерін көрсетумен)
Ғылыми жетекшісі,
Кеңесші
Тапсырманы
қабылдады
(қолы)
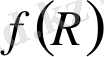 гравитациясы
гравитациясы
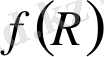 гравитациясы теориясында Нетер симметриясын қолдану
гравитациясы теориясында Нетер симметриясын қолдану
8. Дипломдық жұмысты орындау кестесі
Тапсырманың берілген күні «__»20__ж.
Ғылыми жетекші: PhD, доцент м. а Мырзакулов Е. М.
Тапсырманы қабылдаған: Алтынбек А. М.
МАЗМҰНЫ
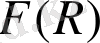 ГРАВИТАЦИЯСЫ . . .
ГРАВИТАЦИЯСЫ . . .
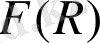 гравитациясы . . .
гравитациясы . . .
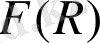 гравитациясы . . .
гравитациясы . . .
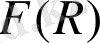 гравитациясы . . .
гравитациясы . . .
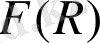 теория гравитациясы және скаляр-тензорлы космология . . .
теория гравитациясы және скаляр-тензорлы космология . . .
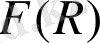 скаляр-тензорлы космологиясында Нетер симметриясы әдістері . . .
скаляр-тензорлы космологиясында Нетер симметриясы әдістері . . .
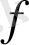 -ЭССЕНЦИЯ ЖӘНЕ
-ЭССЕНЦИЯ ЖӘНЕ
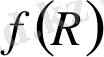 ТЕОРИЯ ГРАВИТАЦИЯСЫ . . .
ТЕОРИЯ ГРАВИТАЦИЯСЫ . . .
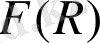 гравитация
гравитация
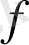 -эссенциясында Нетер симметриясы әдістері . . .
-эссенциясында Нетер симметриясы әдістері . . .
ШАРТТЫ БЕЛГІЛЕУЛЕР МЕН ҚЫСҚАРТУЛАР
- Supernovae type Ia
- Cosmic microwave Background
- (Lambda-Cold Dark Matter)
- Фридман-Робертсон-Уокер
- Фридман теңдеуі
- күңгірт энергия
- күңгірт материя
- Эйнштейн - Гильберт
- Бранс-Дик
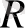
- кеңістіктің скаляр қисықтығы
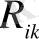
- Риччи тензоры
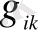
- метрикалық тензор
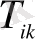
- энергия-импульс тензоры
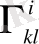
- Кристоффель символы
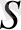
- скаляр өріс үшін әсер
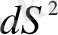
- метрика немесе оқиғалар арасындағы аралық

- материя үшін Лагранж функциясы

- гравитациялық тұракты

- Хаббл параметрі

- масштабты фактор
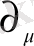 немесе
немесе
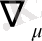
- ковариантты дифференциалдау
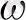
- күй параметрі
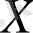
- векторлық өріс
КІРІСПЕ
Тымжаңа Ia жұлдыздары (SN Ia) [1] мен космологиялық микротолқынды фонға (CMB) [2] жүргізілген бақылаулар, Ғаламның үдемелі ұлғаю үстінде екендігін көрсетті. Жалпы салыстырмалық теориясында бұл ұлғаюдың себебін түсіндіруде, космологиялық сұйықтық-күңгірт энергия ұғымы енгізілген болатын [3] . Қазіргі уақытта, ΛCDM моделі (Lambda-Cold Dark Matter) арқылы, Ғаламның
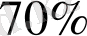 -күңгірт энергия,
-күңгірт энергия,
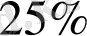 -күңгірт материя және
-күңгірт материя және
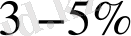 -бөлшектерден тұратындығы анықталды. Күңгірт энергия (КЭ) мен күңгірт материя (КМ) табиғаты қазіргі уақытта белгісіз болып отыр. Кейін, Эйнштейн-Гильберт әсеріне түзету терминін енгізу арқылы құрылған модификацияланған гравитация теориясы негізінде Ғаламның үдемелі ұлғаюын зерттеуде жаңа бағыт ашылған болатын. Мұндай түзету терминдері күңгірт энергияның көмегінсіз өріс теңдеулерін шешімдерін алуға көмектеседі [4] . Жалпы жағдайда, біздің модельде қажетті әсерде
-бөлшектерден тұратындығы анықталды. Күңгірт энергия (КЭ) мен күңгірт материя (КМ) табиғаты қазіргі уақытта белгісіз болып отыр. Кейін, Эйнштейн-Гильберт әсеріне түзету терминін енгізу арқылы құрылған модификацияланған гравитация теориясы негізінде Ғаламның үдемелі ұлғаюын зерттеуде жаңа бағыт ашылған болатын. Мұндай түзету терминдері күңгірт энергияның көмегінсіз өріс теңдеулерін шешімдерін алуға көмектеседі [4] . Жалпы жағдайда, біздің модельде қажетті әсерде
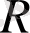 Риччи скаляр терминінің орнына оның жалпыланған
Риччи скаляр терминінің орнына оның жалпыланған
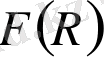 функциясын аламыз. Динамикалық қозғалыс теңдеуін тапқан кезде, әсерді метрикаға (метрикалық формализм) қатысты вариациялаймыз немесе өзара байланыстарын және метриканы тәуелсіз динамикалық айнымалылар деп алып, әсерді жеке қарастыруға болады (Палатиндік формализм) [5] . Бұл теорияға сәйкес, Палатинді формализмде берілген әсер скаляр-тензор түрінде берілген теорияға эквивалентті. Нәтижесінде, Эйнштейн-Гильберт әсерінен өріс теңдеуін аламыз. Палатиндік формализмдегі
функциясын аламыз. Динамикалық қозғалыс теңдеуін тапқан кезде, әсерді метрикаға (метрикалық формализм) қатысты вариациялаймыз немесе өзара байланыстарын және метриканы тәуелсіз динамикалық айнымалылар деп алып, әсерді жеке қарастыруға болады (Палатиндік формализм) [5] . Бұл теорияға сәйкес, Палатинді формализмде берілген әсер скаляр-тензор түрінде берілген теорияға эквивалентті. Нәтижесінде, Эйнштейн-Гильберт әсерінен өріс теңдеуін аламыз. Палатиндік формализмдегі
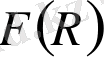 гравитациясы әсерде сызықты емес мүшелер себебінен әртүрлі динамикалық теңдеулерге алып келеді.
гравитациясы әсерде сызықты емес мүшелер себебінен әртүрлі динамикалық теңдеулерге алып келеді.
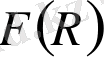 теория гравитациясының, материя Лагранжаны метрикамен байланысқа тәуелді үшінші түрі (метрикалық-аффиндік формализм) бар [7] . Сонымен қатар, Ғаламның динамикасын анықтауда, симметрия ұғымын пайдаланамыз. Оның ішінде, біз Нетер симметриясын қарастырамыз. Нетер симметриясы әдісі арқылы Ғаламның үдемелі ұлғаюын түсіндіретін
теория гравитациясының, материя Лагранжаны метрикамен байланысқа тәуелді үшінші түрі (метрикалық-аффиндік формализм) бар [7] . Сонымен қатар, Ғаламның динамикасын анықтауда, симметрия ұғымын пайдаланамыз. Оның ішінде, біз Нетер симметриясын қарастырамыз. Нетер симметриясы әдісі арқылы Ғаламның үдемелі ұлғаюын түсіндіретін
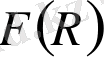 теория гравитациясының тиімді түрін таба аламыз. Сонымен қатар, Нетер симметриясы әдістері Ғаламның динамикасын анықтауда тиімді әдіс болып табылады.
теория гравитациясының тиімді түрін таба аламыз. Сонымен қатар, Нетер симметриясы әдістері Ғаламның динамикасын анықтауда тиімді әдіс болып табылады.
Бірінші бөлімде, гравитацияның классикалық физика және жалпы салыстырмалық теорияларындағы анықтамалары жайлы қарастырамыз. Жалпы салыстырмалық теориясын қарастырамыз.
Сонымен қатар, бұл бөлімде жалпы салыстырмалық теориясының космологиялық зерттеулері арқылы қазіргі уақытта үлкен жетістікке жеткен, физика бөлімі - космология жайлы айтамыз. Ғаламның эволюциясы мен дамуын, сонымен қатар, Ғаламның динамикасын түсіндіретін модельдерді қарастыратын боламыз.
Қазіргі уақытта, жалпы салыстырмалық теориясында үлкен жетістіктерге жеткен космологиялық модельдердің бірі - ΛCDM моделі болып табылады. Космологиялық зерттеулердің нәтижесінде, Ғаламның күңгірт энергия мен күңгірт материядан тұратындығы белгілі болды. Күңгірт энергия мен күңгірт материяның табиғаты қазіргі уақытта ғалымдарға белгісіз. Сонымен қатар, бұл бөлімде, Ғаламның үдемелі ұлғаюын тудыратын күңгірт энергияның табиғатын анықтауда скалр өрісте бірнеше модельдерін атап өтеміз. Соның ішінде, қарастыратын негізгі модельдер: k-эссенция және квитэссенция болып табылады.
Ғаламның үдемелі ұлғаюын түсіндіретін екі анықтама бар, біріншісі күңгірт энергия болса, екіншісі модификацияланған гравитация теориясы болып табылады. Біз, дипломдық жұмыстың екінші бөлімінде, модификацияланған гравитациялар теориясын қарастыратын боламыз. Ғаламның үдемелі ұлғаюын түсіндіретін модификацияланған гравитация теориясының ең тиімді модельдері, олар
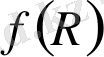 және
және
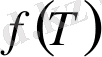 теория гравитация модельдері болып табылады. Біздің жағдайда,
теория гравитация модельдері болып табылады. Біздің жағдайда,
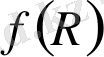 теория гравитациясын қарастыратын боламыз. Кеңістіктің қисықтығы мен оның толтырылған материясын өзара біріктіретін Эйнштейн теңдеуін қарастыратын боламыз. Кеңістікті-уақытты 4-өлшемді Фридман-Леметр-Робертсон-Уокер метрикасын қарастыратын боламыз. Эйнштейн теңдеуінде қисықты скалярды жалпыланған функциясымен алмастыру арқылы қарастыратын боламыз.
теория гравитациясын қарастыратын боламыз. Кеңістіктің қисықтығы мен оның толтырылған материясын өзара біріктіретін Эйнштейн теңдеуін қарастыратын боламыз. Кеңістікті-уақытты 4-өлшемді Фридман-Леметр-Робертсон-Уокер метрикасын қарастыратын боламыз. Эйнштейн теңдеуінде қисықты скалярды жалпыланған функциясымен алмастыру арқылы қарастыратын боламыз.
Қисықты скалярдың жалпыланған функциясы арқылы, Ғаламның үдемелі ұлғаюын күңгірт энергия мен күңгірт материяны ескермей анықтай алатын боламыз.
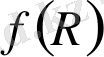 теория гравитациясының метрикалық, Палатиндік және метрикалық-аффиндік формализдерін қарастырамыз.
теория гравитациясының метрикалық, Палатиндік және метрикалық-аффиндік формализдерін қарастырамыз.
Сонымен қатар, бұл бөлімде, скаляр-тензорлы
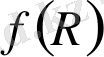 теория гравитациясын қарастырамыз. Скаляр-тензорлы космологияда
теория гравитациясын қарастырамыз. Скаляр-тензорлы космологияда
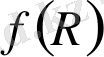 теория гравитациясының метрикалық, Палатиндік және метрикалық - аффиндік формализмдерін қарастырып, әсерді анықтап, қозғалыс теңдеулерін алатын боламыз.
теория гравитациясының метрикалық, Палатиндік және метрикалық - аффиндік формализмдерін қарастырып, әсерді анықтап, қозғалыс теңдеулерін алатын боламыз.
Дипломдық жұмыстың үшінші бөлімінде,
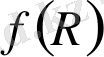 теория гравитациясын және Нетер симметриясын қарастырамыз. Модификацияланған гравитация теориясы ішінде Ғаламның динамикасын анықтауда тиімді модель түрі ол -
теория гравитациясын және Нетер симметриясын қарастырамыз. Модификацияланған гравитация теориясы ішінде Ғаламның динамикасын анықтауда тиімді модель түрі ол -
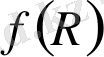 теория гравитациясы болып табылады. Бірақ та, біз қозғалыс теңдеулерін шешімін тапқанда
теория гравитациясы болып табылады. Бірақ та, біз қозғалыс теңдеулерін шешімін тапқанда
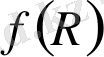 теория гравитациясының бірнеше түрін аламыз. Оның барлықтары бірдей, Ғаламның динамикасын анықтай бермейді. Біз,
теория гравитациясының бірнеше түрін аламыз. Оның барлықтары бірдей, Ғаламның динамикасын анықтай бермейді. Біз,
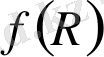 теория гравитациясының нақты түрін анықтау үшін тиімді симметрия түрі Нетер симметриясын пайдаланамыз. Нетер симметриясы әдісі арқылы, Ғаламның динамикасын түсіндіретін
теория гравитациясының нақты түрін анықтау үшін тиімді симметрия түрі Нетер симметриясын пайдаланамыз. Нетер симметриясы әдісі арқылы, Ғаламның динамикасын түсіндіретін
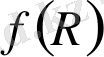 теория гравитациясының түрін анықтай аламыз.
теория гравитациясының түрін анықтай аламыз.
Сонымен қатар, бұл бөлімде скаляр-тензорлы космологияны қарастыратын боламыз. Скаляр-тензорлы космологияда
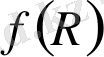 теория гравитациясын өрнектейміз. Сондай-ақ, скаляр-тензорлы космологияда Нетер симметриясы әдісін қолданып нақты шешімдерді алатын боламыз.
теория гравитациясын өрнектейміз. Сондай-ақ, скаляр-тензорлы космологияда Нетер симметриясы әдісін қолданып нақты шешімдерді алатын боламыз.
Дипломдық жұмыстың төртінші бөлімінде, фермиондық өріс
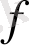 -эссенциясын қарастырамыз.
-эссенциясын қарастырамыз.
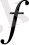 -эссенциясында
-эссенциясында
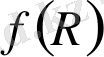 теория гравитациясын қарастырамыз. Сонымен қатар,
теория гравитациясын қарастырамыз. Сонымен қатар,
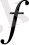 -эссенциясында
-эссенциясында
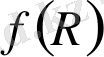 теория гравитациясына Нетер симметриясы әдісін қолданамыз.
теория гравитациясына Нетер симметриясы әдісін қолданамыз.
Зерттелетін тақырыптың өзектілігі: Ғаламның үдемелі ұлғаюын түсіндіретін модель қарастыру.
Зерттелетін тақырыптың мақсаты:
Ғаламның үдемелі ұлғаюын түсіндіретін моделді алу. Нетер симметриясы әдісін қолданып,
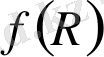 теория гравитациясы нақты мәнін аламыз.
теория гравитациясы нақты мәнін аламыз.
Жұмыстың құрылымы және көлемі: Дипломдық жұмыс кіріспеден, 4 тараудан, қорытындыдан және қолданылған әдебиеттер тізімінен тұрады.
1 ЖАЛПЫ САЛЫСТЫРМАЛЫҚ ТЕОРИЯСЫ ЖӘНЕ КОСМОЛОГИЯ
1. 1 Жалпы салыстырмалық теориясы
Ғаламның негізгі динамикасын, сонымен қатар кеңістікте болып жатқан физикалық құбылыстардың табиғатын түсіндіруде ғалымдар көптеген космологиялық зерттеулер жүргізіліп, өздерінің теорияларын ұсынған болатын. Солардың бірі, А. Эйнштейн ұсынған салыстырмалық теориясы болып табылды. Классикалық физикада, біз білеміз, кеңістікте оқиғаларды бақылағанда уақытты абсолют шама деп аламыз, яғни бір санақ жүйесінен екінші санақ жүйесіне оқиға еш кедергісіз тез уақыт аралығында жетеді. Яғни, белгілі бір уақыт аралығында өтетін оқиғаның жылдамдығы жарық жылдамдығына жуық жылдамдықта өтеді деген сөз. Сонымен қатар, кеңістікте оқиға бақылаушының көзқарасымен салыстырғанда бірдей уақыт аралықтарында өтеді деп жорамалданды. Демек, жылдамдықтары қандай болмасын кеңістікте оқиға бақылаушымен салыстырғанда бірдей уақыт аралықтарын көрсетеді деп айтылады.
Бірақ та, Эйнштейн ұсынған салыстырмалық теориясына сәйкес, кеңістікте болып жатқан оқиғаның ешқайсысы жарық жылдамдығынан жоғары жылдамдықта өтпейтіндігін айтқан болатын. Мұндай жағдайда, уақыттың абсолют екендігіне күмән түседі. Себебі, оқиға жарық жылдамдығына жуық жылдамдықта өткенде, кеңістіктегі оқиға болып жатқан уақыт пен бақылаушының уақыт айырмашылығы болады. Демек, кеңістікте болып жатқан оқиға мен бақылаушы әрқайсысы өзіндік уақытқа ие екен. Кеңістікте оқиғаның орнын анықтау үшін үшөлшемді кеңістікті қарастырамыз. Біз білеміз, салыстырмалық теориясын Эйнштейн арнайы және жалпы салыстырмалық теориясы деп қарастырған болатын. Арнайы салыстырмалық теориясына сәйкес оқиға кеңістікте бірдей уақыт аралығында тұрақты жылдамдықта өтеді. Барлық физика заңдылықтары тұрақты болады. Ал, жалпы саыстырмалық теориясына сүйенсек, кеңістікте оқиға бақылаушымен салыстырғанда уақыт айырмашылығы болатындығы анықталды. Айта кететін бір жайт, салыстырмалық теориясында масса мен энергияның эквиваленттілік теңдеуі:
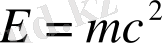 (
(
 -энергия,
-энергия,
 -масса,
-масса,
 -жарық жылдамдығы) . Бұл теңдеуді, Эйнштейн ұсынған болатын. Яғни кеңістіктегі дененің массасы санақ жүйесінде дененің тыныштықтағы энергиясына тең. Кеңістікте дене белгілі бір кинетикалық энергияға ие болады да, ол дененің массасын арттыруға себеп болады.
-жарық жылдамдығы) . Бұл теңдеуді, Эйнштейн ұсынған болатын. Яғни кеңістіктегі дененің массасы санақ жүйесінде дененің тыныштықтағы энергиясына тең. Кеңістікте дене белгілі бір кинетикалық энергияға ие болады да, ол дененің массасын арттыруға себеп болады.
Жалпы жағдайда, жалпы салыстырмалық теориясы-арнайы салыстырмалық теориясының жалпыланған, гравитация теориясы болып табылады. 1915жылдары А. Эйнштейн ұсынған болатын.
Сонымен, классикалық физикаға сәйкес кеңістікте барлық денелер Ньютон ұсынған тартылыс заңына сәйкес гравитация, әсерінен кеңістікте бір-біріне тартылып тұрады. Сондай-ақ гравитация кеңістікте кез-келген уақыт аралығында әсер ететін тартылыс күші болып табылады. Бірақ та, салыстырмалық теориясына сәйкес, кеңістікте ешқандай оқиға жарық жылдамдығынан жоғары жылдамдықта жүрмейді. Гравитацияны түсіндіруде екі көзқарас пайда болған болатын. Сол себепті, кеңістікте оқиғаның өту процесі мен гравитацияны толық әрі нақты түсіндіру мақсатында, жалпы салыстырмалық теориясы ұсынылған болатын. Сонымен жалпы саыстырмалық теориясына сәйкес, кеңістікте оқиға 4-өлшемді кеңістікті-уақытта қарастырылатын болады.
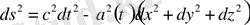 , (1. 1)
, (1. 1)
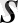 -қашықтық,
-қашықтық,
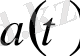 -масштабты фактор,
-масштабты фактор,
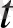 -уақыт,
-уақыт,
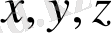 -кеңістікті координаталар.
-кеңістікті координаталар.
Ньютон ұсынған тартылыс заңына сәйкес, кеңістікте барлық дене бір-біріне тартылып тұрады. Мысалы, Күнді айнала қозғалған Жер тартылыс күшінің әсерінен Күн жүйесін тастап кете алмайды. Ал, жалпы салыстырмалық теориясында гравитация дененің массасы әсерінен кеңістікке түсіретін әсері түрінде сипатталады. Яғни дененің массасы үлкен болған жағдайда, ол кеңістікті-уақытта кеңістіктің қисаюын тудырады. Осыдан кейін, жалпы салыстырмалық теориясында кеңістіктің қисықтығы ұғымы пайда болды. Сонымен, Эйнштейн өзінің теориясын ұсынған болатын. Сәйкесінше, бұл теория кеңістікті-уақыттың қисықтығы мен оның толтырылған материяны байланыстырады. Бұл теорияға сәйкес, кеңістікті-уақыт метрикамен анықталады, ал гравитация кеңістіктің қисықтығы түрінде көрініс табады. Сәйкесінше, қисықтық метрикалық тензормен анықталады. Негізінен, кеңістіктің қисықтығы оның материямен толтырылуымен сипатталады, себебі материяның энергиясы қаншалықты үлкен болса, кеңістік соншалықты қисаяды екен. ЖСТ-да кеңістіктің метрикасын анықтау үшін Эйнштейннің теңдеуін анықтайтын боламыз. Эйнштейн теңдеуі - кеңістікті-уақыттың қисықтығы мен оны толтыратын денені байланыстыратын гравитациялық өріс теңдеуі болып табылады.
Яғни, теңдеу келесі түрде көрініс табады
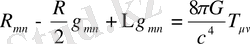 , (1. 2)
, (1. 2)
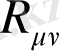 -Риччи тензоры,
-Риччи тензоры,
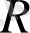 -кеңістіктің қисықтығы,
-кеңістіктің қисықтығы,
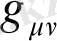 -метрикалық тензор,
-метрикалық тензор,
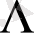 -космологиялық тұрақты,
-космологиялық тұрақты,
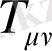 -энергия-импульс тензоры,
-энергия-импульс тензоры,
 -гравитациялық тұрақты,
-гравитациялық тұрақты,
 -жарық жылдамдығы.
-жарық жылдамдығы.
Риччи скалярының мәні
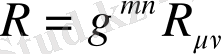 , (1. 3)
, (1. 3)
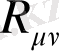 -кеңістікті-уақытта қисықтық тензорын арқылы шешімі табылатын Риччи тензоры болып табылады. Қисықтық тензоры келесі өрнекте сипатталады
-кеңістікті-уақытта қисықтық тензорын арқылы шешімі табылатын Риччи тензоры болып табылады. Қисықтық тензоры келесі өрнекте сипатталады
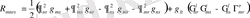 . (1. 4)
. (1. 4)
Метрикалық тензор арқылы анықталатын, Кристоффел символдары арқылы өрнектеледі.
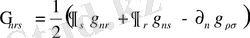 . (1. 5)
. (1. 5)
Эйнштейн теңдеуін анықтап, метрикалық тензор компоненталарын аламыз. Сол арқылы, кеңістікті-уақыттың қисықтығын сипаттай аламыз.
Кеңістікті-уақыттың қисықтығы негізінде кеңістікте қашықтықты аламыз
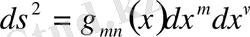 . (1. 6)
. (1. 6)
Эйнштейн теңдеуі Минковский метрикасымен өрнектеледі

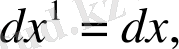
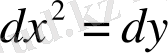 , 7 (1. 7)
, 7 (1. 7)
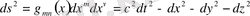 . (1. 8)
. (1. 8)
Эйнштейн теңдеуін шешу бұл метрикалық тензорды анықтау болып табылады. Энергия-импус тензорын анықтау арқылы өрнектейміз. Сол арқылы біз, кеңістікті скаляр, вакуммды, өрісті деп қарастыра аламыз. Сонымен, кеңістікті-уақытта метриканың мәні арқылы біз, космологиялық мәселелердің бірі қисықтықтың мәнін анықтай аламыз. Эйнштейн теңдеуі арқылы, гравитацияның кеңістікті-уақытта қисықтығы екендігін анықтадық.
Классикалық өріс пен жалпы салыстырмалық теориясын байланыстыру үшін ең кіші әсер принципін қолданамыз. Әсер
 Лагранжанның
Лагранжанның
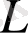 уақыт бойынша интегралы болып табылады
уақыт бойынша интегралы болып табылады
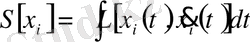 . (1. 9)
. (1. 9)
Классикалық механикада Лагранжан кинетикалық энергия мен потенциалдық энергияның айырмасы ретінде анықталады
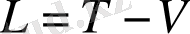 . (1. 10)
. (1. 10)
Классикалық өріс үшін, жүйенің симметриясын көрсететін бірнеше түрлендіруге қатысты Лагранжан өте пайдалы болып табылады. Ең кіші әсер принципін қолданып, Эйлер-Лагранж теңдеуін ала аламыз
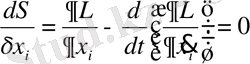 . (1. 11)
. (1. 11)
Жалпы салыстырмалық теориясында гравитацияны сипаттайтын Эйнштейн-Гильберт әсері келесі теңдеумен беріледі
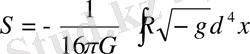 , (1. 12)
, (1. 12)
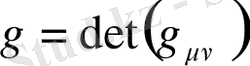 -метрикалық тензор анықтауышы,
-метрикалық тензор анықтауышы,
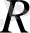 -Риччи скаляры,
-Риччи скаляры,
 -гравитациялық тұрақты. Әсерді шешу арқылы, ЖСТ-ын классикалық өрістермен байланыстыратын қозғалыс теңдеулері алынады.
-гравитациялық тұрақты. Әсерді шешу арқылы, ЖСТ-ын классикалық өрістермен байланыстыратын қозғалыс теңдеулері алынады.
Олай болса, толық әсер Эйнштейн-Гильберт мүшесі мен материяның қосындысы болып табылады, яғни
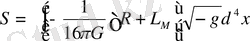 , (1. 13)
, (1. 13)
мұнда,
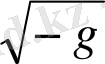 масштабы фактор.
масштабы фактор.
Әсердің принципіне сәйкес, әсерді
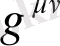 қатысты вариациялағанда 0-ге тең болады
қатысты вариациялағанда 0-ге тең болады
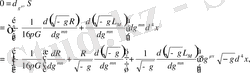 (1. 14)
(1. 14)
бұл
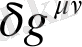 кез-келген вариациясында әділетті болғандықтан, тік жақша ішіндегі өрнек 0-ге ұмтылуы қажет. Осылайша біз келесі қозғалыс теңдеуін аламыз
кез-келген вариациясында әділетті болғандықтан, тік жақша ішіндегі өрнек 0-ге ұмтылуы қажет. Осылайша біз келесі қозғалыс теңдеуін аламыз
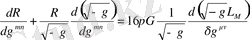 . (1. 15)
. (1. 15)
Теңдеудің оң жағын энергия-импульс тензоры
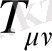 түрінде табамыз
түрінде табамыз
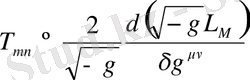 . (1. 16)
. (1. 16)
Қозғалыс теңдеуінен Эйнштейннің өріс теңдеуі шығады. Ол үшін бізге
 және
және
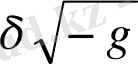 білу қажет.
білу қажет.
 анықтау үшін, Риман тензорынан бастаймыз
анықтау үшін, Риман тензорынан бастаймыз
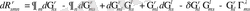 , (1. 17)
, (1. 17)
және вариация
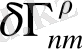 екі байланыстың айырмасы болғандықтан, өзі де тензор болады. Сәйкес, ковариантты туындысы келесі түрде беріледі
екі байланыстың айырмасы болғандықтан, өзі де тензор болады. Сәйкес, ковариантты туындысы келесі түрде беріледі
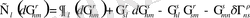 . (1. 18)
. (1. 18)
Осы өрнектен біз
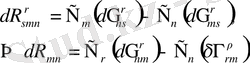 . (1. 19)
. (1. 19)
аламыз.
Риччи скаляры
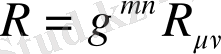 арқылы анықталады. Сонда
арқылы анықталады. Сонда
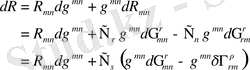 , (1. 20)
, (1. 20)
оң жақтағы екінші мүше толық туынды болып табылады, сол себепті де Стокс теоремасына сәйкес интеграл арқылы шекаралық мүше ретінде өрнектеле алады. Шексіздікте
 метриканы вариациялағанда 0-ге ұмтылады десек, бұл мүше әсерді вариациялағанда ықпал етпейді. Сол себепті де, келесі өрнекті аламыз
метриканы вариациялағанда 0-ге ұмтылады десек, бұл мүше әсерді вариациялағанда ықпал етпейді. Сол себепті де, келесі өрнекті аламыз
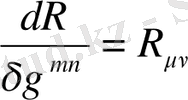 . (1. 21)
. (1. 21)
Енді
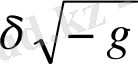 қарастырайық.
қарастырайық.
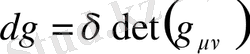 болғандықтан, Якобиан формуласы арқылы оны келесі түрде жазуға болады:
болғандықтан, Якобиан формуласы арқылы оны келесі түрде жазуға болады:
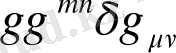 . Содан кейін
. Содан кейін
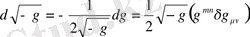 , (1. 22)
, (1. 22)
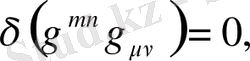 болғандықтан,
болғандықтан,
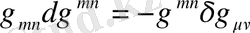 және
және
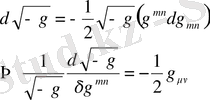 , (1. 23)
, (1. 23)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz