Бернулли кездейсоқ шамаларының мысалдары

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ
М.Өтемісов атындағы Батыс Қазақстан Мемлекеттік Университеті

Математика кафедрасы
Курстық жұмыс
Тақырыбы : ДИСКРЕТТІ КЕЗДЕЙСОҚ ШАМАЛАРДЫ МОДЕЛЬДЕУ

Орындаған : М - 31 топ студенті Салыбай Қ.Қ.
Тексерген : Математика кафедрасының аға оқытушысы Маутеева С.М.

Орал - 2018 жыл

Мазмұны
Кіріспе
2
I. Дискретті кездейсоқ шамалар
4
II. Дискретті кездейсоқ шамалардың модельдері
* 2.1. Бернулли және биномдық үлестірімдер
* 2.2. Гипергеометриялық үлестірім
* 2.3. Геометриялық және теріс биномдық үлестірімдер
* 2.4. Пуассон үлестірімі
8
Қосымша кестелер

Қорытынды

Пайдаланылған әдебиеттер

Кіріспе

I бөлім . Дискретті кездейсоқ шамалар
ξ кездейсоқ шамасының қабылдайтын мәндері ақырлы бүтін сандар немесе тізбек түрінде жазылса, онда ондай ξ кездейсоқ шамасын дискретті кездейсоқ шамалар деп атайды.
Дискретті кездейсоқ шаманы анықтау үшін әдетте таблица құрады. Мұндай таблицада екі жол болады. Оның бірінші жолында кездейсоқ шаманың қабылдайтын мәндері, ал екінші жолында сол мәндерді қабылдау ықтималдықтары жазылады. Сонда ақырлы бүтін мәндер қабылдайтын ξ кездейсоқ шамасы үшін мұндай таблица мынандай:
Мәндер
x1
x2
···
xn
Ықтималдықтар
p1
p2
···
pn
Бұлай құрылған таблицаны ξ кездейсоқ шаманың үлестірім таблицасы деп атайды.
Біз бұдан былай ξ кездейсоқ шамасының үлестірім таблицасын былай жазуға келісеміз: бірінші жолда ξ таңбасы ашады, ал екінші жолдың таңбасын әрқашан p әрпі қойылады. Әрі қарай жоғарыдағы таблица сияқты. Сөйтіп ξ кездейсоқ шамасының үлестірім таблицасы мынау:
X
x1
x2
x3
···
xn
Р
p1
p2
p3
···
pn
Үлестірім таблицасының екі қасиеті бар:
1. Екінші жолда тұрған сандар теріс емес, яғни pi ≫0;
2. Екінші жолда тұрған сандардың қосындысы бірге тең, яғни
i=1npi=1
p1 , p2 ,..., pn сандары ықтималдықтар болғандықтан, өйткені анықтама бойынша pi=Pξ=x , i=1, n, бірінші қасиеттің орындалуы өзіне - өзі түсінікті. Ал, екінші қасиетті алатын болсақ, (1) теңдіктің сол жағы;ξ кездейсоқ шамасының x1, x2,..., xn мүмкін мәндерінің әйтеуір бірін қабылдайтындығын көрсеткеннен келіп шығады.
Егер ξ кездейсоқ шамасы саналатын x1 ,x2 ,..., xn ... мәндерін қабылдаса, онда оның үлестірім таблицасы жоғарыдағы сияқты жасалады, бірақ (1) теңдігінің орнында
i=1infinitypi=1
теңдігі тұрады.
Мысал:
1.1. Екі ойын сүйегін лақтырғанда пайда болатын ұпайлардың қосындысының үлестірім таблицасын табу керек.
Шешуі: Екі ойын сүйегіндегі ұпайлардың қосындысы ξ арқылы белгілейік. ξ - дің қабылдайтын мәндері: 2, 3, 4 , ... , 12. Енді осы мәндерді қандай ықтималдықтармен қабылдайтындығын есептесек, мынандай үлестірім таблицасы шығады;
ξ
2
3
4
5
6
7
8
9
10
11
12
p
136
236
336
436
536
636
536
436
336
236
136

II бөлім . Дискретті кездейсоқ шамалардың модельдері
Әрбір кездейсоқ шама өзінің оқиғалар кеңістігінен белгілі бір ықтималды таңдау арқылы алынатындықтан, оларға сәйкес келетін айнымалылар мен сынақтарды санаттап класстарға бөлуге болады. Әрбір кластағы кездейсоқ шамалардың жалпы ортақ үлестірім заңдары мен белгісіз параметрлері болады. Осы үлестірім заңдарының класстары ықтималдықтық (ықтималды) модельдер деп аталады. Осы бөлімде біз дискретті кездейсоқ шамалар үшін ықтималдықтық модельдердің негізгі төрт түрін сипаттап, олардың қолданыс ортасын мысалдармен көрсетеміз.
2.1 Бернулли және биномдық үлестірімдер
Бернулли үлестірімі. Бернулли сынағы немесе эксперименті деп нәтижесі сәтті немесе сәтсіз деп санатталатын сынақты айтады. X Бернулли кездейсоқ шамасы деп сынақ сәтті аяқталса, 1 мәнін қабылдайтын сәтсіз аяқталса, 0 мәнін қабылдайтын шаманы айтамыз.
2.1.1 - мысал
Бернулли кездейсоқ шамаларының мысалдары.
1. Әдеттегі Бернулли сынағына бүк және шік нәтижелері, сәйкесінше, сәтті және сәтсіз болып саналатын, тиынды лақтыру сынағын жатқызуға болады.
2. Өндірістен кездейсоқ өнімді алу сынағында X Бернулли кездейсоқ шамасы 1 және 0 мәндерін өнімнің, сәйкесінше, ақаулы немесе ақаусыз болуына байланысты қабылдайтын кездейсоқ кездейсоқ шаманы келтіруге болады.
3. Өнімнің төзімділігін үзіліссіз қанша уақытқа шыдайтынын тексеретін сынақта Бернулли кездейсоқ шамасы 1 мәнін, егер 1500 сағаттан астам уақыт жұмыс істесе (сәтті), 0 мәнін қарама - қарсы жағдайда қабылдайды.
4. Екі сақтандырғышты ақаулыққа тексеретін сынақты қарастыратын болсақ, Бернулли кездейсоқ шамасы 1 мәнін, егер сақтандырғыштың екеуі де ақаусыз болса, 0 мәнін басқа қалған жағдайларда қабылдайды.
Егер сәттіліктің ықтималдығы p және сәтсіздіктің ықтималдығы 1-p болса, онда X - тің үлестірім заңы мен үлестірім функциясы төменгідей болады:
X
0
1
p(x)
1-p
P
F(x)
1-p
1
X кездейсоқ шамасының дисперсиясы σX2 немесе Var(X) белгіленіп, төменгідей анықталады:
X кездейсоқ шаманың дисперсиясының жалпы анықтамасы
σX2=E[X-uX2] (2.2)
Мұндағы uX=E(X) X- тің математикалық күтімі. Кез келген дискретті жиынтықтың дисперсиясы осы жиынтықты анықтайдын кездейсоқ шаманың дисперсиясына сәйкес келеді. Ал σX2 дисперсиясын есептейтін оңайырақ формула (сонымен қатар, кейде оны қысқаша формула деп атайды) келесідей:
X кездейсоқ шаманың дисперсиясының қысқаша формуласы
uX=p , σX2=EX2-EX2=p-p2=p(1-p) 2.1.1
2.1.2 - мысал
Электр өнімінің 5500 уақыт бірлігінен астам уақыт үздіксіз жұмыс жасау ықтималдығы 0.1 болсын. X кездейсоқ шамасы 1 мәнін, егер кездейсоқ алынған өнімнің 5500 уақыт бірлігінен астам уақыт үздіксіз жұмыс жасаса қабылдасын да, 0 мәнін басқа жағдайларда қабылдасын. X-тің орта мәні мен дисперсиясын есептеңіз.
Шешуі:
Мұндағы X шамасының сәттілік ықтималдығы p=0.1 болатын Бернулли кездейсоқ шамасы болып табылады. (2.1.1) - сәйкес, uX=0.1 және σX2=0.1x0.9=0.09 .
Биномдық үлестірім. Әрқайсысында сәттілік ықтималдығы p болатын, бір - бірінен тәуелсіз орындалатын n Бернулли сынағын қарастырайық. Осы n Бернулли сынақтарын бірге қарастыратын болсақ, бұл сынақты биномдық сынақ деп атаймыз.
Биномдық кездейсоқ шаманы n Бернулли сынақтарындағы барлық сәттіліктер санын есептейді.
Әдеттегі биномдық сынақ ретінде тиынды n рет лақтыру сынағы болып табылады. Y биномдық кездейсоқ шаманы осы n сынақтағы бүктер санын есептесін. Бірақ, 2.1.1 - мысалда жазылған басқа Бернулли сынақтарының тәуелсіз қайталанулары да биномдық сынақ болып табылып, оған сәйкес биномдық кездейсоқ шамалары анықтала алады. Мысалы, өндіріс орнынан n өнім кездейсоқ алынып, олардың әрқайсысын ақаулыққа тексеретін болсақ, ол Бернулли сынағы болады да, егер өнімдер бір-бірінен тәуелсіз ақаулы немесе ақаусыз болса, онда тексерістен өткен өнімдердің ақаулылар саны биномдық кездейсоқ шаманы береді.
Егер i - Бернулли сынағына сәйкес Xi Бернулли кездейсоқ шамасы болса, яғни
Xi=10 , i=1,...,n,
онда Y биномдық кездейсоқ шамасы
Y=1nXi (2.1.2)
Y биномдық кездейсоқ шамасы егер n Бернулли сынақтарының барлығы сәтсіз аяқталса, онда 0 мәнін, және, егер n Бернулли сынақтарының барлығы сәтті аяқталса, n мәнін қабылдайды. Y-тің оқиғалар кеңістігі SY=0,1,...,n. Биномдық кездейсоқ шаманың үлестірім функциясы екі параметр бойынша қадағалап отырады. Олар - n сынақтар саны және n Бернулли сынағының әрқайсысында шығатын сәтті нәтиженің ықтималдығы. Егер Y~Bin(n,p) болса, онда бұл биномдық үлестірімге ие Y кездейсоқ шаманың параметрлері n және p екенін көрсетеді де, оның үлестірім заңы py=P(Y=y) болып, келесі формула арқылы есептеледі:
Биномдық үлестірімнің ықтималдықтық үлестірім заңы
PY=y=nypy(1-p)n-y , y=0,1,...,n. 2.1.3
Бұл формуланың дәлелдеуі алдымен, тәуелсіздік шартын қойғанымызды ұмытпау керек те n Бернулли сынақтарының қатарына тек y дана 1 болатындығының ықтималдығы py(1-p)n-y және осындай қатарлардың саны ny болғаннан шығады. 2.1 - суретте n=20 үшін үш биномдық үлестірім заңдары белгіленген. p=0.5 болғанда үлестірім заңы симметриялы болады, p=0.3 және p=0.7 болса, үлестірім заңдары бір - біріне айна қатесіз симметриялы болады.
Биномдық үлестірім үшін PY=y үлестірім функциясының айқын формуласы жоқ, бірақ қосымшада келтірілген 1 - кестеде n=5,10,15 және 20 үшін p - ның белгілі бір мәндеріне үлестірім функциясының мәндері келтірілген. Биномдық (n,p) үлестірімінің кез келген n мен p мәндеріне сәйкес үлестірім заңы мен үлестірім функциясын алу үшін келесі R пәрмендерін қолданамыз:
Биномдық үлестірімнің үлестірім заңы мен үлестірім функциясын алу үшін қолданылатын R пәрмендері
dbinom(y, n, p) # y=0,1,...,n үшін PY=y үлестірім заңын береді
pbinom(y, n, p ) # y=0,1,...,n үшін PY=y үлестірім функциясын береді

Жоғарыдағы R пәрмендерінде y 0 - ден n - ге дейінгівектор мәндерді де қабылдай алады. Мысалы,
- dbinom(4, 10, 0,5) пәрмені 0.2050781 нәтижесін береді, себебі бұл тиынды 10 рет лақтырғанда төрт бүк шығудың ықтималдығын есептейтін пәрмен немесе Y~Bin(10, 0.5) үшін PY=4 көрсететі.
- dbinom(0:10, 10, 0,5) пәрмені Y~Bin(10, 0.5) үшін үлестірім заңын қайтарады. Ал Bin(10, 0.5) үлестірімінен таңдама алу үшін sample немесе жаңа rbinom пәрмендерін қолдансақ болады. Мысалы, sample(0:10, size=5, replace = T , prob = dbinom(0:10, 10, 0.5)) және rbinom(5, 10, 0.5) пәрмендерінде тиынды 10 рет лақтыру сынағын бес рет қайталағанда әрқайсысында шығатын бүк санын көрсетеді.
- sum(dbinom(4:7, 10, 0.5)) және pbinom(7, 10, 0.5) - (pbinom(3, 10, 0.5) пәрмендерінің екеуі де 0.7734375 мәнін қайтарып, P3Y=7=F(7)-F(3) есептейтін пәрмендер
n және p параметрлері бар биномдық X кездейсоқ шамасының орта мәні мен дисперсиясының формулалары келесідей:
Биномдық үлестірімнің орта мәні мен дисперсиясы

EX=np , σX2=np(1-p) (2.1.4)

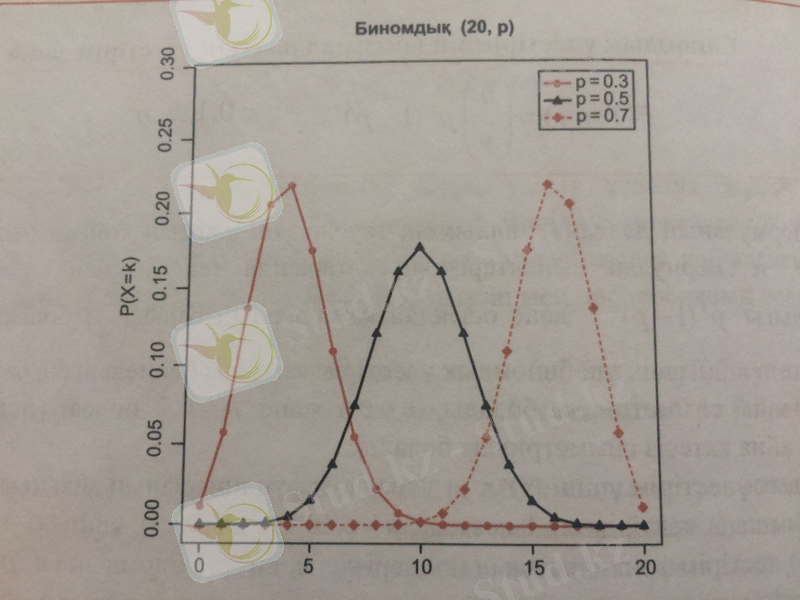
2.1 - сурет. Бірнеше биномдық үлестірім заңдары
n=1 үшін биномдық кездейсоқ шама Бернулли кездейсоқ шамасы болады да, жоғарыдағы орта мән мен дисперсияның формулалары (2.1.1) формулаларына түрленеді.
2.1.3 - мысал
Көздің түсі сияқты адамның физикалық ерекшелігінің бірі анасынан, екіншісі әкесінен берілетін ген жұптары арқылы беріледі. Әрбір ген доминанты D немесе рецесивті R бола алады. DD , DR және RD ген жұптарына ие адам физикалық ерекшелікке ие деп атаймыз. Бала бірдей ықтималдықпен ата - анасының әрқайсысының бір ген аладыдеп ескерейік. Егер ата - анасының екеуі де гибритті ген жұптарына ие болса (яғни, екеуі де DR және (RD) гендеріне ие), олардың төрт баласының үшеуінде өздеріндей гендерге ие болады деген оқиғаның ықтималдығын табыңыз.
Шешуі
X кездейсоқ шамасы төрт баланың нешесі ата - анасындай генге ие екенін көрсетсін. Әрбір бала Бернулли сынағын көрсетеді. Бұл сынақтағы сәттілік (бала ата - анасындай физикалық ерекшелікке ие) ықтималдығы p=PDD+PRD+PDR=0.25+0.25+0.25=0.75. Төрт Бернулли сынақтары бір - біріне тәуелсіз және X~Bin(4, 0.25) .(2.1.3) формуласы бойынша,
PX=3=430.7530.251-0.422 .
2.1.4 - мысал
Белгілі бір дүкендегі сатылымдардың 70% - ы кредит карталарымен жасалады. X кездейсоқ шамасы келесі 10 сатылымда кредит картасын қолданған сатылымдар санын көрсетсін. а) X - тің үмітті мәні мен дисперсиясын; ә) P(5=X=8) ықтималдығын табыңыз.
Шешуі
а) Әрбір сатылым Бернулли сынағы болады. Оның сәтті аяқталуын сатылымды кредит картамен төлеу деп анықтаңыз. 10 Бернулли сынақтарының бір - бірінен тәуелсіз деп ұйғарайық, сонда X~Bin10, 0.7 болады. Яғни (2.1.4) формуласы бойынша
EX=np=100.7=7 σX2=10(0.7)(0.3)=2.1 .
ә) Егер ab болса, онда PaX=b=Fb-F(a) және 1 - кесте бойынша
P5=X=8=P4=X=8=F8-F4=0.851-0.047 =0.804
pbinom(8, 10, 0.7)-pbinom4, 10, 0.7 R пәрмені 0.8033427 жауабын қайтарады. Басқа жолмен есептесек,
P5=X=8=PX=5+PX=6+PX=7+PX=8
=1050.750.35+1060.760.34+1070.770.3 3+1080.720.32
=0.103+0.200+0.267+0.233=0.803 (2.1.5)
sum(dbinom(5:8, 10, 0.7) R пәрмені де жоғарыдағы R пәрмені қайтарған жауапты береді.
2.1.5 - мысал
Сотта айыпталушы кінәлі деп танылу үшін 12 сыншының кемінде сегізі оған кінәлі деген дауыс беру керек. Әрбір сыншы бір - бірінен тәуелсіз 0.7 ықтималдықпен дұрыс шешім қабылдайтыны белгілі. Егер айыпталушылардың 40% -кінәлі болмаса, қабылданатын дұрыс шешімдердіің үлесі қандай?
Шешуі
Дұрыс шешімдер үлесі P(B) арқылы белгілейік, мұндағы B=сыншы дұрыс шешім қабылдайды. Егер A=айыпталушы кінәлі емес деп белгілесек, Толық ықтималдық формуласы бойынша
PB=PBAPA+PBACPAC=PBA0.4+PBAC0.6 .
X арқылы осындай сынақ дұрыс шешім беретін сыншылар санын белгілейік. Мұндағы, әрбір сыншы Бернулли сынағы болады, ол сынақ сәтті деп сыншының дұыс шешімін аламыз. Барлық Бернулли сынақтыры тәуелсіз болғандықтан, X~Bin12, 0.7. Егер айыпталушы кінәлі болмаса, кінәлі емес деген шешім дұрыс және егер айыпталушы кінәлі болса, кінәлі деген шешім дұрыс болатынын есте сақтау керек. Сондықтан,
PBA=PX=5=
1-k=0412k 0.7k0.312-k=0.9905
және
PBAC=PX=8=k=81212k0.7k0.3k=0.724
Бұдан,
PB=PBA0.4+PBAC0.6=0.8306
шығады.
2.2 Гипергеометриялық үйлестірім
Көлемі ақырлы және N болатын жиынтықта M1 дананы 1 деп белгілеп, қалған M2=N-M1 дананы 0 деп белгілейік. Оған көлемі n болатын қарапайым таңдау жасалады. Осындай сынақ жасалғанда қарастырылатын модельді гипергеометриялық модель деп атайды. X арқылы таңдамадағы 1 деп белгіленген даналар санын белгілейік те, оны параметрлері M1 , M2 және n болатын гипергеометриялық кездейсоқ шама деп атайық.
Ақырлы жиынтықтардан жасалатын таңдаулар экологияны да өзіне қосатын бірнеше мағынаға ие; 2.2.1 - мысалды қараңыз. Гипергеометриялық үлестірімнің техникалық қолданысының протипі ретінде үлестіруші деңгейінде сапаның бақылауы болып табылады. N данадан тұратын партия үлестірушіге түседі. Үлестіруші көлемі n болатын қарапайым кездейсоқ таңдау жасап, таңдаманың әрбір данасын белгілі - бір ақауға тексеру. X гипергеометриялық кездейсоқ шамасы таңдамадағы ақаулы өнім данасын санайды.
Бұл протипті гипергеометриялық сынақта әрбір өнім тексерісі Бернулли сынағы болып, сәтті оқиға деп өнімнің ақаулы болуын айтамыз. Барлық Бернулли сынақтарында сәттіліктің ықтималдығы p=M1N. Егер Xi Бернулли кездейсоқ шамасы i - өнім тексерісіндегі сәттілік немесе сәтсіздікті көрсетсе, X гипергеометриялық кездейсоқ шамасы
X=i=1nXi (2.2.1)
арқылы анықталады. (2.1.2) өрнегі биномдық кездейсоқ шама өрнегіне ұқсас. Гипергеометриялық сынақтың биномдық сынақтан айырмашылығы, сынақтағы Бернулли сынақтары бір - бірінен тәуелсіз емес. Өйткені, екінші Бернулли сынағындағы сәттіліктің шарты ықтималдығы бірінші сынақтағы сәттіліктің шартсыз ықтималдығынан өзгеше болады. Таңдамадағы ақаулы өнімдер саны аспайды. Мысалы, егер партияда N=10 дана өнім болса, оның M1=5 данасы ақаулы болса, көлемі n=6 болатын таңдама жасалса, таңдамадағы ақаулы өнімдер саны бестен аспайды. Таңдама көлемі n=6 болатын соңғы мысалда ақаулы өнімдер саны нөл бола алмайды. Себебі партияда тек бес ақаусыз өнім бар; яғни көлемі алты болатын таңдамада кемінде бір ақаулы өнім болады деген сөз. Сонымен, жалпы айтқанда, гипергеометриялық M1 , M2 ,n үлестірілген X кездейсоқ шаманың оқиғалар кеңістігі 0,1,...,n жиынының ішжиыны болады. Дәл сондай ішжиын екені мәтінге байланысты анықталады, бірақ оның матаматикалық тілдегі жалпы сипаттамасы келесідей:
SX=max0.n-M2,...,min⁡(n,M1) , (2.2.2)
мұндағы maxa1,a2 және min⁡(a1,a2) арқылы, сәйкесінше, a1 және a2 сандарының үлкен және кішісін белгілейміз.
Қарапайым кездейсоқ таңдаулар бойынша, көлемі n болатын M1+M2n таңдамалартең ықтималдықты. Сондықтан, осы мысал үшін құрамында дәл x дана ақаулы өнім бар таңдаманы M1xM2x жолмен алуға болса, гипергеометриялық M1 , M2 ,n үлестіріміне ие X кездейсоқ шамасының үлестімі заңы төменгідей анықталады
Гипергеометриялық үлестірімнің үлестірім заңы

PX=x=M1nM2n-xM1+M2n 2.2.3

Биномдық жағдайдағыдай, егер xn болса, онда P(X=x)=0. Осыған қоса, егер xM1 немесе n-xM2 болса, онда P(X=x)=0, себебі, сәйкесінше, таңдамада жиынтыққа қарағанда 1 - лер саны немесе 0 - дер саны көп болмайды. Осыны, егер x 2.2.2 - де келтірілген оқиғалар кеңістігіне тиісті болмаса, онда P(X=x)=0 деп қысқаша жазса болады.
3.8 - суретте n=10, N=60 және M1 - дің түрлі мәндері үшін гипергеометриялық үлестірім заңының графигі бейнелеген. Егер M1=30 болса, p=M1N=0.5 және үлестірім заңы симметриялы болады, ал M1=15 және M1=45 болса, онда олардың графиктері бір - біріне айна қатесіз симметриялы болады.
Гипергеометриялық кездейсоқ шаманың үлестірім функциясының аналитикалық түрі жоқ. Гипергеометриялық M1 , M2 ,n X кездейсоқ шаманың үлестірім заңы мен үлестірім функциясы кез келген M1 , M2 және n үшін төмендегі R пәрмендері арқылы табыла алады:

Гипергеометриялық үлестірімнің үлестірім заңы мен үлестірім функциясын алу үшін қолданылатын R пәрмендері
dhyper (x, M1, M2, n) # (2.2.2) - де берілген S_x - тегі x үшін P(X=x) үлестірім заңын аламыз.
phyper (x, M1, M2, n) #(2.2.2) - де берілген S_x - тегі x үшін P(X=x) үлестірім функциясын аламыз.

Жоғарыдағы R пәрмендерінде x Sx - тен алынған бүтін сандар векторы бола алады. Мысалы, егер Y гипергеометриялық 30, 30, 10 кездейсоқ шамасы болмаса,
-dhyper(4, 30, 30, 10) пәрмені 0.2158315 мәнін P(Y=4) үшін қайтарады.
-dhyper0:10, 30, 30, 10 пәрмені Y - тің үлестірім заңын береді. Сонда, гипергеометриялық 30, 30, 10 үлестірімінен үлестірімінен таңдаманы sample пәрмені немесе жаңа rhyper пәрмені арқылы алса болады. Мысалы,
sample(0:10, size=5, replace=T, prob=dhyper0:10, 30, 30, 10)
және rhyper(5, 30, 30, 10) пәрмендерінің екеуі де гипергеометриялық 30, 30, 10 үлестірімінен көлемі беске тең таңдама береді.
-sum(dhyper(4:7, 30, 30, 10)) және phyper7, 30, 30, 10-rhyper(3, 30, 30, 10) пәрмендерінің екеуі де P3Y=7=F7-F(3) ықтималдығын есептеп, 0.8106493 мәнін береді.

2.2 - сурет. Кейбір гипергеометриялық үлестірім заңдары
Гипергеометриялық (M1=N-M2, n) үлестірімге ие X кездейсоқ шамасының орта мәні мен дисперсиясы келесідей:
Гипергеометриялық үлестірімнің орта мәні мен дисперсиясы

μ=nM1N, σX2=nM1N1-M1NN-nN-1 (2.2.4)

2.2.1 - мысал
Он екі тоңазытқыш қайталанып шығатын шу ақауы бар болғандықтан, үлестірушіге кері қайтарылады. Осы он екі тоңазытқыштың төртеуінде ақаулы компрессор болса, қалғандары одан жеңіл ақауға ие. Ақауды түзету үшін алты тоңазытқыш кездейсоқ алынады. X кездейсоқ шамасы таңдамадағы ақаулы компрессорларға ие тоңазытқыштар данасын санайды. X-тің оқиғалар кеңістігін анықтап, P(X=3) тауып X-тің үмітті мәні мен дисперсиясын табыңыз.
Шешуі
Мұнда N=12 , n=6 және M1=4. Сонда, X-тің оқиғалар кеңістігі SX0,1,2,3,4 . 2.2.3 формуланын ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.