Эйнштейн теңдеулері

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

Сырдария университеті

Жаратылыстану факультеті

Жоғары математика және физика кафедрасы

Жоба тақырыбы: ӘЛЕМНІҢ ӨЗГЕРІСІН СИПАТТАУДА ЭЙНШТЕЙН ТЕҢДЕУЛЕРІН ЗЕРТТЕУ

Мамандығы: 5В011000-Физика
Курс: 2
Бағыт: Физика және математика
Секция: Жаратылыстану және математика ғылымдарындағы иновациялық зерттеулер

Студенттің аты-жөні: Меккам Е.
Ғылыми жетекшісі: Қазақбаев Ж.Б.
ғ.м., аға оқытушы

Жетісай 2021
МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .3

1 ЭЙНШТЕЙН ТЕҢДЕУЛЕРІ ЖӘНЕ ЭКСПЕРИМЕНТАЛЬДЫ ДӘЛЕЛДЕНУІ
1.1 Эйнштейн теңдеулері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 5
1.2 Эйнштейн теориясының экспериментальды түрде анықталуы және Әлемнің қарқынды кеңеюінің дәлелі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ...10

2 ЭЙНШТЕЙН ТЕҢДЕУЛЕРІ ЖӘНЕ ОНЫҢ НАҚТЫ ШЕШІМДЕРІ
2.1 Нетер теоремасы. Фермионды өрістің гравитациямен байланысынан қозғалыс теңдеулерін алу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...13
2.2 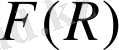гравитациясымен эссенциясының фермионды өріспен байланысын Нетер теоремасы арқылы шешімін алу ... ... ... ... ... ... ... ... ... ... ... ... 16

ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..20

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... . ... ... ... ... ...21

КІРІСПЕ

Жұмыстың өзектілігі. XX ғасырдың II - жартысында фундаментамендальді теориялық физика, яғни, жалпы физиканың бағыты табиғат заңдарын сипаттауда геометриялық жолға түсті. Бұл жолдан шыққан негізгі бағыттар Арнайы және Жалпы Салыстырмалылық Теориясы болып табылады. Арнайы және Жалпы Салыстырмалылық Теориясы кеңістік - уақыт пен материяның ең негізгі жалпы ұсталған бағытта өзара әсерлесулерін қарастырады. Жалпы Салыстырмалылық Теориясының ең негізгі түсінігі (ЖСТ) кеңістік - уақыттың евклидтік емес геометриясында (оның қисықтығында) гравитациялық өзара әсерлесулердің табиғаты болып табылады. Бұл бағыт бойынша электрлік және магниттік күштерді біріктіріп жасаған Максвелдің еңбегінен соң, 1916 жылы Альберт Эйнштейн Ғаламның төрт өлшемді және гравитациямен байланысты ЖСТ - ның негізін ашты. Мүмкіндігі жоғары бұл теория алғашқы кезеңдерде тәжірибенің жеткіліксіздігінен экспериментальді дәлелденбеген теория, яғни, ғалымдар бастапқыда мойындамаған болып табылды. Осы Эйнштейннің гравитациялық теориясының негізінде физикада жаңа ашылулар пайда болды.
Жалпы салыстырмалық теориясы өрісті сипаттайтын негізгі теория болып табылады. Осы ауқымды теорияның негізінде Эйнштейн теңдеулері жатыр. Эйнштейн теңдеулері - сызықты емес II-ретті дифференциалдық теңдеулер болғандықтан, олардың нақты шешімдерін анықтау күрделі және өзекті мәселе болып табылады.
Ғылыми жобаның мақсаты:
Заманауи математикалық аппаратты пайдаланып, ЖСТ-да гравитациялық өрісті сипаттайтын Эйнштейн теңдеулерінің жаңа және нақты шешімдерін анықтау.
Жұмыстың міндеттері. 1. Ғаламның эволюциясын сипаттайтын космологиялық модельдер құру болып табылады.
2. Осы құрылған модельдердегі алынған динамикалық теңдеулердің нақты шешімдерін анықтап, олардың қазіргі таңда белгілі астрофизикалық бақылаулар нәтижесімен салыстыру.
Зерттеу деңгейі. Бұл жұмыстағы алынған нәтижелердің барлығы тек теориялық тұрғыдан қарастырылады. Мұнда алынған нәтижелер белгілі шешімін табалмай жүрген астрономиялық бақылау мәліметтерін түсіндіруге мүмкіндік береді.
Зерттеу объектісі. Космология
Зерттеу пәні. Теориялық физика
Зерттеу әдісі. Бұл жұмыста төмендегі әдістер қолданылды:
1. Сызықты емес дифференциалдық теңдеулерді шешу үшін заманауи математикалық аппараттың әдістері пайдаланылды.
2. Риман геометриясы, тензорлық және векторлық анализдің математикалық физика әдістері, классикалық өріс теориясында қолданылатын математикалық аппарат қолданылады.
Күтілетін нәтиже: Эйнштейн теңдеулерін шығара отырып, күй параметрін анықтап және соның негізінде Әлем бейнесін сипаттайтын графиктер алу.
Дерек көздері. Негізгі алынған дерек көзіміз интернет сайттары және әдебиеттерде берілген теориялық физика кітаптар.
Жұмыстың құрылымы. Кіріспе, екі тарау және қорытынды, пайдаланылған әдебиеттер тізімінен тұрады.

1 ЭЙНШТЕЙН ТЕҢДЕУЛЕРІ ЖӘНЕ ЭКСПЕРИМЕНТАЛЬДЫ ДӘЛЕЛДЕНУІ

1.1 Эйнштейн теңдеулері

1916 жылы Д. Гильберт Эйнштейннің негізгі жұмысынан екі аптадан соң вариациялық принциптен алынған ЖСТ - ның бірінші теңдеуі болып табылатындығы туралы мақаласын жариялады. Гильберт ЖСТ - да гравитациялық өріс үшін әсер келесі түрге ие болатындығын көрсетті:

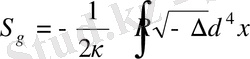, (1.1)

мұнда - көлемнің инвариантты элементі (минус белгісі - кеңстік - уақыт көптүрлілігінің сигнатурасы болып табылады). (1.1.) - әсері кейде гравитациялық өріс үшін Эйнштейн - Гильберт әсері деп аталады. Оның көмегімен ЖСТ есептерін вариациялық тұжырымын жүйелеуге болады [5,15].
Енді гравитациялық өріс + өрістің бөлшектері физикалық жүйесін яғни, жинақталған әсер түрінде сипатталған көрінісін келесі формуламен жазайық:

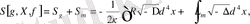(1.2)

мұнда 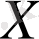- бөлшектің координатасын сипаттайтын жинақталған символ 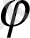- өрістің өзгермелі жүйесін сипаттайды (гравитациядан айырмашылық есебінен), 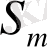- өрістің - бөлшегі жүйе бөлігі үшін әсер, 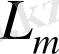- осы жүйе бөлігі үшін 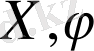және олардың туындысынан тәуелді Лагрианжиан болып табылады. Бір қарағанда (1.1) әсерінде гравитациялық өріс + өрістің бөлшектері жүйе бөлігі әсерлесуінде бір мүшелер жетпейтін сияқты болып көрінеді. Бірақ түптеп келгенде, мұндай әсерлесулер нақтыланып қойылған. Шын мәнінде мұндай әсерлесулер осыған дейін ескеріліп қойылған, яғни, 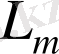- лагрианжианында өрістің барлық дербес туындылары ковариантты түрге ауыстырылған, ал барлық ұйытқулар 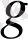римандық метрикасының көмегімен орындалады. Мұндай әдіс материя мен гравитацияның өзара әсерлесулері есебінен Жалпы Салыстырмалылық Теориясы үшін нақты және қарапайым түрде болып табылады. Ол гравитациялық өріс және материяның минимальды өзара әсерлесуі деп аталады. Эйнштейн теңдеуін қорытып шығару үшін экстремумдары берілген метрика бойынша, (1.2) - теңдеуін вариациялау арқылы аламыз. Әсер принципі бойынша әсер өзгерісінің кері метрикамен қатынасы нольге тең екенін көреміз:

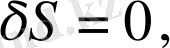(1.3)
онда

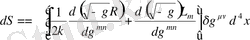
Сонымен бұл теңдеу 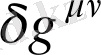-дің кез-келген вариациялануында орындалуы қажет, яғни бұл келесі түрде өрнектеледі:

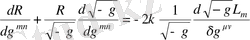, (1.4)

Алынған теңдеу өріс метрикасы үшін қозғалыс теңдеуі болып табылады. Теңдеудің оң жақ бөлігі энергия - импульс тензорына пропорционал болады:

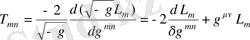, (1.5)

Теңдеудің сол жақ бөлігін есептеу үшін 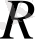Риччи склярын және метрика анықтауышын вариациялауымыз қажет.
Біз Риччи скалярын вариациясын есептеу үшін алдыменен Риман қисығының тензорын және Риччи тензорының варициясын анықтауымыз керек [8]. Осылайша, Риман қисықтық тензоры келесі формуламен өрнектеледі:

, (1.6)

Риман қисықтығы тек ғана Леви - Чивита 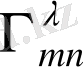-байланысына тәуелді және Риман тензорының вариациясы келесідей жолмен анықталады:

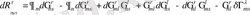, (1.7)

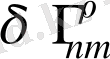-екі байланыстың айырмашылығы болып табылады және біз енді осы өрнектің ковариантты туындысын келесідей есептейміз:

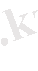
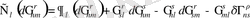
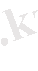(1.8)

Енді біз жоғарыда келтірілген Риман қисықтығы тензорының вариациясы үшін өрнекпен екеуінің арасындағы айырмашылықты байқай аламыз:

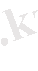
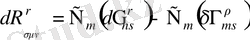, (1.9)

Сонымен Риччи қисықтық тензорының вариациясын Риман тензорының вариациясымен байланыстыра отырып келесідей өрнекті аламыз:

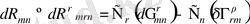, (1.10)

Риччи скаляры келесі түрде анықтаймыз:

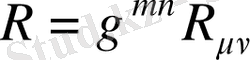(1.11)

Осылайша, 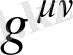кері метрикасына қатысты байланысы келесі түрде:

,
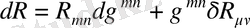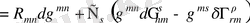, (1.12)

Екінші қатарда біз жоғарыда алынған шешімдерді Риччи қисығы вариациясы мен ковариантты туындының 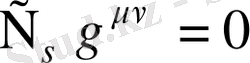метрикалық үйлесімділігі үшін қолдандық.
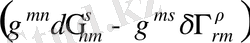
Соңғы мүшені 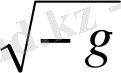-ге көбейте отырып толық туындыны аламыз, оны келесі түрде жазамыз:

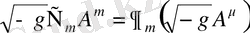, (1.13)

Сонымен Стокс теоремасы бойынша тек интегралдаған кезде шекаралық мүшені береді. Осыдан егер 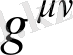-метрикасының өзгерісі шексіздікте нольге айналса, бұл термин әсердің вариациясын өзгерте алмайды. Осылайша біз келесі өрнекті аламыз:

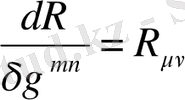, (1.14)

Ендігі кезекте біз анықтауышты вариациялауды қарастырамыз. Якоби формуласы анықтауышты дифференциялауда негізгі ереже болып табылады және ол келесі түрде:

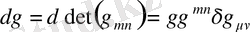, (1.15)

мұнда 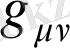- диагоналін координата жүйесінде түрлендіруге болады, сосын басты диагоналда дифференциалданған көбейтінді козффициенті үшін көбейтінді ережесі ретінде қабылауға болады. Осының көмегімен біз мынаны аламыз:

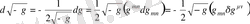, (1.16)

Cоңғы теңдікте біз мынаны пайдаландық:

, (1.17)

Матрицаны кері дифференциалдау ережесіне сәйкес келесіні көреміз:

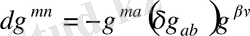, (1.18)

Осылайша анықтауышты вариациялау бойынша біз келесідей қорытынды жасаймыз:

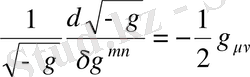, (1.19)

Енді бізде барлық керекті мәндер бар және осы мәндерді өріс метрикасы үшін қозғалыс теңдеуіне қойып, келесідей қорытынды өрнекті аламыз:

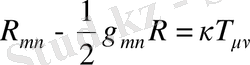. (1.20)

Бұл Эйнштейннің өріс теңдеуі деп аталады және мұндағы 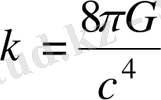осыған тең болады. Сонымен Эйнштейн - Гильберт әсерін вариациялау арқылы ЖСТ - ның негізгі теңдеуін қорытып шығардық
Эйнштейн теңдеуі - қисық кеңістік - уақыттың метрикасын оны толтырып тұрған материямен байланыстыратын ЖСТ - дағы гравитациялық өріс. Ол келесі түрде жазылады[18]:

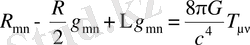(1.21)

мұндағы - космологиялық тұрықты, 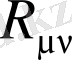- Риччи тензоры, ол кеңістік - уақыттың қисықтық тензорынан индекстер жұбы бойынша ұйытқудан алынады:

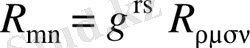(1.22)

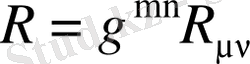(1.23)

мұндағы 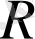- скалярлық қисықтық, ол Риччи тензоры және 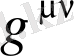метрикалық тензорды ұйытқылау нәтижесінде алынады. Ал 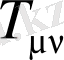- материяның энергия - импульс тензоры болып табылады, с - вакуумдағы жарық жылдамдығы, - Пи саны, - Ньютонның гравитациялық тұрақтысы. 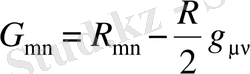тензорын Эйнштейн тензоры деп атайды[2,9]. Эйнштейн теңдеуінің мынадай негізгі жалпылама қасиеттерін қарастырайық:
1. Эйнштейн теңдеуі 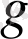риман метрикасының компоненттеріне қатысты екінші ретті дербес туындылы 10 сызықты емес дифференциалдық теңдеулер жүйесін құрайды. Бейсызықтылықтың физикалық қасиетін былайша түсіндіруге болады. ЖСТ - ның негізгі идеясына сәйкес гравитациялық өріс кез - келген энергия түрі арлықы пайда бола береді. Алайда, гравитациялық өрістің өзінде де энергия болады. Осылайша, гравитациялық өріс өзін - өзі тудыра алады және осы қасиет теңдеулердің сызықты еместігімен айқындалады. Сонымен қатар, осы қасиеттен суперпозиция принципінің орындалмайтындығы шығады: Эйнштейн теңдеуінің екі шешімінің қосындысы, жалпылама жағдайда бұл теңдеудің шешімі бола алмайды. Алайда, әлсіз гравитациялық өріс жағдайында, суперпозиция принципі жуықтап орындалады.
2. Он Эйнштейн теңдеулері төрт тепе - теңдікті қанағаттандырады, сондықтан шын мәнінде тек алты теңдеу ғана тәуелсіз болады, осы алты теңдеуден метриканың он компонентінен алтауын ғана табуға болады. Қалған мәндер ЖСТ - ның жалпы коварианттылық қасиетін көрсетеді: әрбір нүктедегі он компоненттің төртеуіне жалпы координаталық түрлендіру барысында 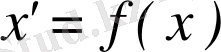функциясының көмегімен еркін мәндерді беруге болады. Осылайша, гравитациялық өріс жалпы жағдайда алты тәуелсіз физикалық еркіндік дәрежелеріне ие болады. Қалған еркіндік дәрежелерінің координаталарын кейде электромагниттік теориямен салыстырып калибровка деп те атайды.
3. ЖСТ - ның негізгі міндеті гравитациялық өрістің қуат көзін және симметрия түрін (аксиальді, сфералық, жазық, біртекті кеңістік т.б.) анықтау болып табылады. Симметрияның әрбір типі үшін метриканы оңай түрде жаза алатын координата жүйесі бар. Метриканың осындай қарапайым түрі үшін Эйнштейн теңдеуін құра отырып, белгілі бір дербес туындылы дифференциалдық теңдеулер жүйесін аламыз. Бұл теңдеулердің сызықты еместігінен математикалық физиканың стандартты әдістері көп жағдайда нәтиже бермейді, сондықтан Эйнштейн теңдеуін интегралдау үшін арнайы әдістерге жүгінген ыңғайлы[11,12,14].
4. Қуат көзі жоқ Эйнштейн теңдеуі, яғни 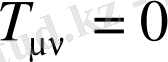жағдайында, келесі әмбебап түрге енеді

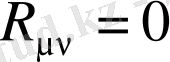. (1.24)

Максвелл электродинамикасындағы жағдайдан айырмашылығы, 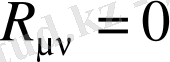- дің сызықты еместігінен бұл теңдеудің ешқандай жалпы шешімі белгілі емес.
5. Мынадай 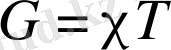түрдегі теңдеуі басқа да эквивалентті көріністерде жазылуы мүмкін.
6. Геометризациялау принципін сатылап қолдану тұрғысынан, ЖСТ толықтай аяқталмаған теория, өйткені Эйнштейн теңдеуінің оң жағындағы энергия - импульс тензоры - гравитацияның қуат көзі әлі де геометризацияланбаған[3,4,5].
1916 жылы Эйнштейн ЖСТ - ның негізгі теңдеулері жазылған белгілі жұмысын алғаш рет жарыққа шығарғанынан бірнеше апта өткен соң, Д. Гильберт осы теңдеулерді вариациялық принциптен қорытып шығарып, өзінің мақаласын жариялады. Сол себептен, кейде ЖСТ - ның гравитациялық өріс теңдеулерін Эйнштейн - Гильберт теңдеулері деп те атайды.

1.2 Жалпы салыстырмалы теориясының экспериментальды түрде анықталуы және Ғаламның қарқынды кеңеюінің дәлелі

Жоғарыда атап айтқанымыздай, гравитациялық өрісті сипаттайтын 1916 жылы құрылған Эйнштейннің ЖСТ - да Ғаламды сипаттауда негізгі және маңызды теория болып табылады. Осы ЖСТ бойынша қазіргі кезде экспериментальды түрде бақылаулармен дәлелденген жетекші гравитациялық теория болып табылады [6,7,8,9,10]. Айта кетсек, Меркурий перигелиінің ығысуы, уақыттың гравитациялық кешігуі, гравитациялық өрісте сигналды кідіруі, гравтитациялық қызыл ығысу, тартылыс өрісінде Күн сәулесінің ауытқуы және т.б бірқатар бақылаулар көмегімен сәтті түрде тексерілді.
Эйнштейн 1911 жылы бақыланатын траекторияның және гравитациялық линзалау әсері кеңістік - уақыттың қисықтығына байланысты екенін білді және ол траекторияның қисықтығының өлшемін есептеді. 1916 жылы ол Ньютондық теориясынан ЖСТ - дағы жарықтың таралуының жылжуы екі есе көп екенін анықтады. Сонымен бұл теорияның ең негізгі алғашқы зерттеуі 1919 жылы Артур Эддингтон Күннің толықтай тұтылуы кезінде, оның айналасындағы жұлдыздардың көрінбейтіні ЖСТ - ның болжамына сәйкес келетінін дәлелдеді [17,18].
1922 жылы бірінші болып барлық Ғаламды сипаттау үшін Эйнштейн теңдеуін қолданды. Сәйкесінше Эйнштейн теңдеуі қазіргі кезде стандартты космологиялық модельдің негізі болып табылады. Бұл теория барлық ғаламды сипаттау үшін қолданғанымен, бір жағынан алғанда осы теорияның қолданудың да өзіндік шекаралары болады. Ол қазіргі кейбір космологиялық мәселелерді толықтай түсіндіруге қауқарсыз болып табылады. Мәселен, Ғаламның мүмкін айналулары, Ғаламның бариондық ассимметриясы, вакуумдық энергияны және тағыда ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.