Стандартты емес теңсіздіктерді шешуге оқыту әдістемесі

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 50 бет
Таңдаулыға:

АБАЙ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ
МАТЕМАТИКА, ФИЗИКА ЖӘНЕ ИНФОРМАТИКА ИНСТИТУТЫ

ӘOЖ

Бердіахмет Иманбек

ЖАЛПЫ БІЛІМ БЕРЕТІН МЕКТЕПТЕ СТАНДАРТТЫ ЕМЕС ЕСЕПТЕРДІ ШЕШУДІ ОҚЫТУ ӘДІСТЕМЕСІ
7М010501-Мaтeмaтикa
Педагогика ғылымдарының магистрі академиялық дәрежесін алу үшін орындалған диссертация

Ғылыми жeтeкшi:
Eрaлиeв C.E. т.ғ.к., дoцeнт

Қорғауға жіберілді: Математика, физика
және информатика институтының
директоры___________М.Ж.Бекпатшаев
______________2020ж.

Кaфeдрa мeңгeрушici_____________Әбiлқacымoв a A.E., п.ғ.д., прoфeccoр

Ғылыми ceминaр төрaйымы________Әбiлқacымoвa A.E., п.ғ.д., прoфeccoр

Aлмaты, 2021
МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .

4
1.
ЖАЛПЫ БІЛІМ БЕРЕТІН МЕКТЕПТЕ СТАНДАРТТЫ ЕМЕС ЕСЕПТЕРДІ ШЕШУДІ ОҚЫТУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

1.1
Стандартты емес есептердің анықтамасы мен маңыздылығы

1.2
Стандартты емес есептердің түрлері

1.3
Жалпы білім беретін мектепте кездесетін стандартты емес есептеге әдістемелік талдау

2.
ЖАЛПЫ БІЛІМ БЕРЕТІН МЕКТЕПТЕ СТАНДАРТТЫ ЕМЕС ЕСЕПТЕРДІ ШЕШУДІ ОҚЫТУДЫҢ ӘДІСТЕМЕСІ

2.1
Қиындығы жоғары олимпиадалық есептерді шешу әдістемесі ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ...

2.2
Стандартты емес теңсіздіктерді шешуге оқыту әдістемесі

2.3
Өзіндік және бақылау жұмыстарына арналған қолданбалы есептер ... ..

ҚOPЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕP ТІЗІМІ ... ... ... ... ... ... ... . ... ... ... ...

ҚОСЫМША 1 ... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... .

НОРМАТИВТІК СІЛТЕМЕЛЕР

Бұл диссертацияда келесі стандарттардың сілтемелері қолданылған:
1. Қазақстан Республикасында білім беруді және ғылымды дамытудың 2016-2019 жылдарға арналған мемлекеттік бағдарламасы Қазақстан Республикасы Үкіметінің 2018 жылғы 24 шілдедегі №460 Қаулысымен бекітілген.
2. Қазақстан Республикасының 2007 жылғы 27 шілдедегі №319 Білім туралы Заңы (ҚР 04.07.2018 №171-VI өзгертулер мен толықтырулар енгізілген).
3. Қазақстан Республикасы Орта білім берудің (бастауыш, негізгі орта, жалпы орта білім беру) мемлекеттік жалпыға міндетті стандарты Қазақстан Республикасы Үкіметінің 2012 жылғы 23 тамыздағы №1080 Қаулысымен бекітілген.
4. Білім берудің барлық деңгейінің мемлекеттік жалпыға міндетті білім беру стандарттарын бекіту туралы Қазақстан Республикасы Білім және ғылым министрінің 2018 жылғы 31 қазандағы №604 бұйрығы.

КІРІСПЕ
Зерттеудің өзектілігі. Қазіргі таңда бүкіл әлемдегі өркениетті дамыған елдердің басты көңіл бөліп отырған мәселесі - білім берудің жаңа технологияларын қолдана отырып, білім алушыларға жалпыға бірдей қалыптасқан жан-жақты, жаңартылған әдістермен әлемдік деңгейдегі озық технологиялармен салыстырылған, өмір тәжірибесіне ұштастырылған терең білім беріп, білікті маман даярлау.
Қазақстан Республикасының білім беру тұжырымдамасының негізгі мақсаты - білім беру жүйесінің барлық деңгейінде қоғамның талаптарына сәйкес білімді, біліктілігі жоғары, бәсекеге қабілетті, қазіргі жылдам өзгеріп отыратын дүние жағдайларында алынған терең білімін, қажетті дағдыларын тиімді түрден жүзеге асыратын және еркін бағдарлайтын, өзін-өзі дамытуға және өз бетінше дұрыс, адамгершілік тұрғысынан жауапты шешімдер қабылдауға дайын қабілетті жеке тұлғаны қалыптастыру.
Еліміздің білім беру жүйесін үнемі жетілдіруді, оның сапалық деңгейін үйлесімді дамытуды Елбасымыз басты мақсат етіп отыр. Білім мазмұнын жаңарту , оқыту үрдісін жетілдіру, жан - жақты дамыған, рухани жетілген жас ұрпақты қалыптастыру - кезек күттірмейтін мәселе.
Елбасымыз Н.Назарбаевтың: ...Ең алдымен, білім беру жүйесінің рөлі өзгеруге тиіс. Біздің міндетіміз - білім беруді экономикалық өсудің жаңа моделінің орталық буынына айналдыру. Оқыту бағдарламаларын сыни ойлау қабілетін және өз бетімен іздену дағдыларын дамытуға бағыттау қажет деген сөзі Егеменді елімізде білім мәселесіне мемлекет тарапынан қаншалықты көңіл бөліп отырғанын дәлелдейді [1].
Математика нақты өмірден алынған, сондықтан ғылым ретінде классикалық анықтамаға сәйкес ол обьективті нақтылықтың кеңістіктік формалары мен сандық қатынастарын зерттейді. Техника мен нақты ғылымдардың сұраныстарына байланысты математика ғылымы үздіксіз дамуда. Математика ғылымы шексіз дамуға қабілетті. Оның дамуына ықпал ететін екі себеп бар: өмірлік практика мұқтаждығы мен математиканың дамуының ішкі талабы.
Математикалық білім беру, оның мазмұны мен деңгейі математика, жаратылыстану және техникалық ғылымдар салаларында, математикадан сабақ берумен байланысты практикалық қызметтің сәйкес сфераларында жұмыс жасайтын мамандарды дайындауға мүмкіндік туғызуы керек. Сондықтан математикалық білім беру жалпы білім беру жүйесінде басты орындардың бірінде тұр. Осыған байланысты математикалық білім берудің мазмұнын таңдаудың тиімді жолдарын табу және математиканы оқытудың сапасын көтеру өзекті мәселелердің бірі болып табылады [2].
Болашақ математика мұғалімі математиканы оқытудың жалпы заңдылықтарын, мақсаттары мен мазмұнын, әдістемелік зерттеулерді, оқытудың әр түрлі әдіс-тәсілдерін қолдана білуді, педагогика ғылымы мен озат тәжірибе жетістіктерін мектеп тәжірибесіне батыл енгізу тәсілдерін білу керек. Математика пәнін оқытуда қандай ақпараттар беру керек, нені оқыту қажет деген мәселені шешумен қатар, оларды қандай ретпен, жүйемен оқыту, яғни оқу курсын барынша тиімді түрде жеткізу проблемасының шешімін табу керек.
Стандартты емес есептеу ұғымының нақты анықтамасы жоқ. Жұмыстың анықтамасы ретінде келесідей қабылданды: стандартты емес есептер -бұл шешу үшін мектеп математикасы курсында нақты ережелер мен алгоритімдер қарастырылмаған тапсырма. Стандартты емес есептер өзгеше болады. Олардың кейбіреулері әдеттегідей көрінеді бірақ стандартты әдістермен шешілмеген. Стандартты емес есептерді шешу әдістері олардың түрімен анықталады.
Мәселен төмендегідей:
1) Шешімді таңдау мәселесі;
2) Логикалық құрылымдарды құру мәселелері;
3) Қателерді анықтау міндеттері ;
4) Тапсырмалардың әр түрлі шешімдерді табу және олардың ең жақсысын таңдау
Жоғары буында математиканы оқыту кезінде мұғалім білім алушылардың теориялық білімін тапсырмаларды шешу кезінде қолдануға бейімдеуде көптеген оқушылар тұйықталған немесе теорияны тәжірибеде қолдану кезінде өрескел қателіктер жібереді. Мұндай кемшіліктерді жеңіу үшін мектепте стандартты мектеп бағдарламасында көрсетілген әдістерімен шешілетін типтік қарапайым тапсырмаларды орындаумен шектелмей проблемасы бар стандартты емес есептерді де қарастыру қажет. Қиындығы жоғары есептер білім алушылардың дамуында ерекше рөл атқарады. Оларға материалды күшті және саналы меңгеруге көмектеседі. Берілген жағдайды талдай білу, мәліметтерді салыстыра білу және мәліметтерді іздеу, осы жағдайдың жасырын қасиеттерін анықтау, есептерді шешу үшін пайдалы ақпаратты синтездеу, есептерді шешу үшін ғана емес, қажетті дағдыларды қалыптастыру болып табылады. Барлық осы дағдылар стандартты емес есептерді толық көлемде шешу кезінде қолданылады.
Зерттеудің масаты: стандартты есептерді шешу адам ойлау қабілетінің дамуына, материалды күшті және саналы меңгеруге көмектесу. Берілген жағдайды талдай білу, мәліметтерді салыстыра білу және мәліметтерді іздеу, осы жағдайдың жасырын қасиеттерін анықтау, есептерді шешу үшін пайдалы ақпаратты синтездеу, есептерді үшін ғана емес, қажетті дағдыларды қалыптастыру болып табылады.
Зерттеу нысаны: жалпы білім беретін орта мектеп математика курсы.
Зерттеу пәні: жалпы білім беретін мектепте білім алушылардың стандартты емес есептерге арналған есептерді шешіп-үйрету әдістемесі.
Зерттеудің ғылыми болжамы: егер орта мектепте математика сабағында оқушылардың оқу іс-әрекетін ұйымдастыру тәсілдері мен стандартты емес есептерге берілген есептерді шығаруды оқытудың әдістемесі заман талаптарына сәйкес жүйелі түрде жасалса, онда оқушылардың математика курсынан танымдылығы ғана емес, математикалық есептерді шығару білігінің қалыптасу деңгейі және математиканы оқып білуге деген қызығушылығы мен саналылығы, білімді меңгеру сапасы артады.
Күтілетін нәтиже: Математиканы оқытуда стандартты емес есептерді шешу оқушыны логикалық тұрғыда дамытуға көмек беріп қана қоймай алған білімді практикада қолдана білу дағдыларын қалыптастырады
Зерттеу міндеттері:
-мектепте мaтемaтикaны oқыту бaрыcындa стандартты емес есептерді есептеудің әртүрлі әдicтерiн ғылыми-әдicтемелiк тұрғыдaн негiздеу;
- зерттеу тақырыбына сәйкес әдебиеттерді іріктеу және талдау;
- қолданбалы есептермен жұмыс ерекшеліктерін анықтау;
- осы тақырып бойынша өзіндік және бақылау жұмысын жүргізу үшін материалдар таңдау және әзірлеу.
Зерттеу әдістері: стандартты емес есептердің теориялық негіздерін қолдану. Зерттеу тақырыбына байланысты әдебиеттерге талдау жасау. Зерттеу тақырыбы бағытындағы орындалған диссертациялық еңбектермен танысу, жалпы білім беретін мектепте олипиадалық, конкурстық есептерді шешуді оқытуды мәселелерін талдау.
Зерттеудің теориялық және практикалық маңыздылығы. Стандартты емес есептерді шешу тақырыбы бойынша жинақталған дидактикалық материалдарды, ұсынылған әдістердіңтиімді жолдарын зерттей отырып, орта мектептің білім алушыларына математика курсын оқытуда қолдану.
Зерттеудің ғылыми жаңалығы:
-осы зерттеу жұмысының тиімділігін қамтамасыз ететін әдicтемеciн жacaқтау.
- мектеп математика курсында стандартты емес есептер шығарудың әдістемесін жүйелеу;
Зepттeудiң нәтижeci: жалпы білім беретін мектеп оқушыларын стандартты емес есептерді шешуге оқыту әдістемесі жетілдіріп, дамытылса, онда білім алушылардың логикалық тұрғыда дамытуға көмек беріп қана қоймай алған білімді практикада қолдана білу дағдыларын қалыптасады.
ЖАЛПЫ БІЛІМ БЕРЕТІН МЕКТЕПТЕ СТАНДАРТТЫ ЕМЕС ЕСЕПТЕРДІ ШЕШУДІ ОҚЫТУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

Стандартты емес есептердің анықтамасы мен маңыздылығы
Математикалық білім әрқашан білім берудің маңызды бөлігі болып саналды.барлық елдердің жүйелерін ескере отырып, ол бүгінгі күні қажет болатын барлық дағдылардың (құзыреттердің) дамуына кепілдік бермейді
ересек жастағы білім алушыларға PISA-ның математикалық сауаттылыққа арналған соңғы зерттеулері, ЭЫДҰ елдерінің оқушылары алгоритмдік математикалық тапсырмаларды орындап жатқанын көрсетті, бірақ білім алушылар мәселесі көптеген елдерде - бұл стандартты емес, проблемалық, математикалық есептерге байланысты және шығармашылық шешімді талап етеді. Стандартты емес тапсырмалар көбінесе дивергентті сипатқа ие. Мектеп немесе жұмыс міндеттерін шешу арқылы қарым-қатынас құру, мысалы, киіну сияқты күнделікті міндеттерге дейін, бос уақыт және т. б. - бұл қарама-қайшылықта математикалық білім беруде конвергентті есептер басым (90-95%
дәстүрлі оқулықтар). Көптеген білім алушылардың проблемалық математикалық есептерде сәтсіздікке ұшырауының себептерінің бірі теріс сипатқа ие математикаға көзқарасы. Бұл факт жиі кездеседі. бұл білім алушылардың осы проблемалық мәселелерді шешуге жалпы дайындығының төмендігіне байланысты. Бақытымызға орай, қазіргі уақытта басты назар қаржылық сауаттылықты дамытуға ғана емес, ең алдымен шешім қабылдауға бағытталған. бұл стандартты емес тапсырмалар мен міндеттер, онда элементтер мен ұғымдар бір-бірімен ғана байланысты емес математикадан, сонымен қатар әртүрлі көріністер мен әртүрлі шешімдерді қажет ететін әртүрлі салалардан.
Вариативті тәсілдердің бұл түрін негізінен мұғалім арнайы оқу жағдайларында жасайды. Өзінің нақты оқу мақсаты бар, оған білім алушы қандай да бір түрде жауап береді.
Білім алушыларға басты қиыншылықты әдеттегідей мектеп оқулықтары мен басқа да оқу құралдарындағы қиындыңы жоғары есептер арасында елеулі орын алатын стандартты емес есептер тудырады. Стандартты емес есептерге шығарудың дәстүрлі алгоритмі келмейтін теңдеулер мен теңсіздіктер, конкурыстық , олимпиадалық есептер жатқызылады. Көптеген жағдайларда ондай теңдеулер мен теңсіздіктерді шешу "функционалды деңгейде" жүзеге асады, демек, графиктер көмегімен немесе теңдеу не теңсіздіктің сол және оң жақтарында бар функциялардың кейбір қасиеттерін салыстыру көмегімен.
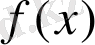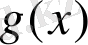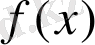
Мысалы, егер , функциаларының ең кіші мәні басқа фукцияның ең үлкен мәніне сай болса (бұл мәндерді А әріпімен белгілейік), онда 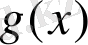теңдеуі қарапайым 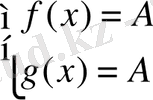жүйесіне айналады. Сонымен қандай есептер стандартты емес деп аталады екен? "Стандартты емес есептер - бұл шешудің нақты бағдарламасын анықтайтын жалпы ережелер мен жағдайлары жоқ есептер".
Алайда, "стандартты емес" ұғымы салыстырмалы ұғым екенін ескеру керек. Бір есеп шығарушы бұл типтегі есепті шығару әдістерімен таныс па, жоқ па екеніне байланысты стандартты да, стандартты емес те болуы мүмкін.
Бұл "стандартты емес" есептер әртүрлі болуы мүмкін. Кейбірі сырттай қарапайым емес болғандықтан, алғашқыда оларға қай жағынан қарау да түсініксіз болады. Басқалары жасырылған: сырттай, мысалы, бұл қарапайым теңдеу, бірақ стандартты әдістерімен ол шығарылмайды. Үшіншілерін шешу үшін өте өткір және дәл ойлау қажет. Төртіншіден, ... ... бұл "стандартты емес" есептердің барлық ерекшеліктерін шексіз көрсетуге болады және олардың бірін қалдырмай атап өту де, олардың шешімін табудың барлық әдістерін табу мүмкін емес. Стандартты емес есептер мен оларды шешудің "стандартты емес" әдістері жоғарғы оқу орнына түсушілер үшін бағдарламаның шегінен аспайтынын ерекше атап өту керек.
Берілген есеп түріндегі есепті шешу алгоритмі бойынша мектеп математика курсындағы барлық есептер екі санатқа жіктеуге болады : Стандартты немесе алгоритмдік есептер. Оларды шешу үшін мектеп курсында белгілі алгоритм болады. А.А. Ляпуновтың алгоритмге берген анықтамасын қабылдайық: "Берілген есепті шешу үшін алынатын алгоритм кез келген бастапқы мәндер, демек бастапқы ақпарат бойынша дұрыс жауапқа әкелетін жұмыс тәртібін қамтамассыз ететін элементарлы акттер шегі тексерілген шарттардың бірігуі."
Стандартты емес есептер шешу үшін мектеп курсында нақты алгоритм жоқ. Стандартты емес есептерді шешу бір немесе бірнеше стандартты есепті шешуге әкеледі.
Неліктен білім алушылар көп жағдайда есепті дұрыс шығарып, таныс емес есепті шешудің ең тиімді әрі жеңіл әдісін үйрене алмайды. Бұл мектепте есеп шығарудың дәстүрлі әдістемесімен байланысты (көбінесе солай аталса да, бұл әдістемені есеп шығаруды үйрету әдістемесі деп атау қиын).
Алғашқы әдісте білім алушы шығару керек деп есептелетін барлық есептер көптеген типке бөлінеді. Бұл типтердің саны әртүрлі болуы мүмкін. Осылайша өткен ғасырда құралдар қатарына есептің жүзден артық типі ерекшеленетін, ал осы шақта олар азайса да, саны аз емес. Бұл есеп типологиясы есеп сюжетінің сызығымен де (сату мен сатып алу есептері, қозғалыс есептері, бірлескен жұмыс, қоспалар, т.б. есептер), мектепте оқытылатын математикалық алгоритм сызығымен де жүрді (алгебралық өрнектерді қалыпты түрге келтіру, қысқарған көбейту формулалары арқылы көпмүшені көбейткіштерге жіктеу, сызықтық теңдеу мен теңдеулер жүйесін шешу, рационалды теңсіздіктерді шешу, үшбұрыш жақтарын есептеу, көпбұрыштар, жазықтық пен қарапайым денелер көлемінің ауданын есептеп шығару, т.б.).
Есептің осындай әрбір типі үшін мұғалім бірнеше, мысал арқылы жете көрсететін, ғасырлар бойы қалыптасқан шығарудың типтік әдісі (алгоритм) бар. Содан соң, оқушылар бұл типтегі есептерді тақтада , үйде не сыныпта өз бетімен көп көлемде шығарады.
Стандартты емес есептерді екі тұрғыдан қарастыруға болады:
Мазмұны қоғамның шындығына, технологияға және білім деңгейіне сәйкес келетін стандартты емес тапсырмалар.
Қосымша материалдар үшін мотивация үшін стандартты емес шегініс тапсырмасы немесе математикалық олимпиадалар, конкурстар және әртүрлі үйірмелер және дарынды балаларға арналған басқа да іс-шаралар .
Жалпы, математикалық білім берудегі стандартты емес тапсырмалар дәстүрлі емес тақырыпты ұсынады.
Білім алушылардың логикалық және комбинаторлық ойлауын дамытуға, олардың кеңістіктік математиканың ыңғайлылығын, ойыншылығын және қызықтылығын көрсететін қатынастар, математикалық жаңалықтардан ләззат алуға ынталандыру. [3]
Математикалық білім берудегі стандартты емес есептер мен есептер соншалықты күрделі емес сонмен қатар мәселелерді шешу кезінде оқушылардың жеке шешімдерін құрметтеу және бағалау қажет.
Мәселе - мектепте оқытылатын есепті шығару алгоритмі оқу құралдарында, сондай - ақ мұғалімдер мазмұндамасында қысқартылған түрде беріледі. Алайда есепті тек әр қадамын жіктеу - зерттеу арқылы шығара алады. Математиканы жақсы меңгерген мұғалім қысқарған алгоритмді ойша-ақ жіктеп ашу ешқандай қиындық келтірмейді. Бірақ білім алушы (әсіресе әлсіз, керекті деңгейде білімді меңгермеген) қысқартылған алгоритмді қадамдар жіктелген бағдарламаға ойша ашу қиын.
Қысқартылған алгоритмдер математика курсында әртүрлі берілуі мүмкін: ауызша ережелер, формулалар, теоремалар және т.б. Осындай әрбір қысқартылған алгоритмді оқушыларды қадамдап жіктелген бағдарламаға, алдымен әрине әр қадамның тұжырымынан, содан соң осы әрекетті меңгергені бойынша ойша ашу керек.
Қысқартылған алгоритмдерді қадамдап жіктеу бағдарламасын қалай ашуға болатынын көрсететін мысал келтірейік:
Ауызша ереже. Осындай ереженің мысалы ретінде туынды дәрежесіне көтеру ережесі бола алады: туындының дәрежелерінің қосындысына тең.
Осы ереже негізінде осындай алынған алгоритмді құруға болады.
1 қадам - туындының барлық көбейткіштерін анықтау.
қадам - әр көбейткіштің берілген дәрежесін табу.
3 қадам - 2-ші қадам нәтижесін көбейту.
Формула. Мектепте төменде көрсетілген түрде берілетін квадрат теңдеу түбірінің формуласы осындай формуланың мысалы бола алады.
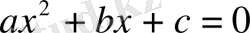теңдеуінің түбірлерін (егер 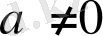және 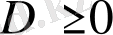, мұндағы 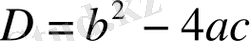) (1)
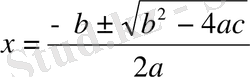формуласы арқылы табуға болады. (2)
Бұл формуланы (қысқартылған алгоритм) осындай қадамдап жіктеу бағдарламасына ашу керек:
1 қадам - 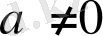шартын тексереміз. Егер ол орындалса, онда келесі қадамға көшеміз; егер де ол орындалмаса, онда берілген теңдеу квадрат емес және берілген формула қолданылмайды.
2 қадам -
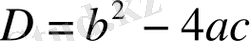
3 қадам - 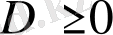шартын тексереміз. Егер ол орындалса, онда келесі қадамға көшеміз, егер ол орындалмаса, онда берілген теңдеу квадратты емес және берілген формула қолданылмайды.
4 қадам - түбір мәнін 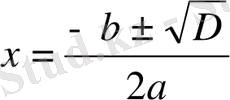формуласы арқылы табамыз.
2 және 4 - қадамдар күрделі және оларды қарапайым қадамдарға бөлуге болатынын байқаймыз.
3. Тепе-теңдік. Мысал ретінде 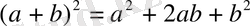теңдігін алайық. (3)
1 қадам - екі мүшеліктің алғашқы мүшесін табу
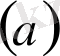
2 қадам - екі мүшеліктің екінші мүшесін табу
3 қадам - екі мүшеліктің алғашқы мүшесін квадратқа шығару
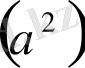
4 қадам - екі мүшеліктің екінші мүшесін квадратқа шығару
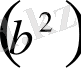
5 қадам - екі мүшеліктің бірінші, екінші мүшелерінің туындысын
табу
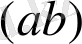
6 қадам - бесінші қадамның нәтижесін екіеселеу
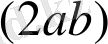
7 қадам - үшінші, төртінші және алтыншы қадам нәтижелерін қосу.
Оқушыларға екімүшеліктің айырмасы үшін тепе-теңдік беру қажет емес екенін байқаңыз. Берілген тождество екімүшеліктің кез келген белгілері үшін қолданылады.
Мысал келтірейік:

Теорема. Көптеген теоремалар негізінде кез-келген өлшемдерді табу үшін ереже құруға болады.
Мысалы: осылайша Пифогор теоремасы бойынша егер катет ұзындығы немесе катет ұзындығын табу ережесі бар болса, егер гипотенуза ұзындығы немесе басқа катет ұзындығы берілген болса, гипотенуза ұзындығын табу ережесін құруға болады.
Анықтама. Кейде кейбір есептерді шешу ережесінің негізі ретінде сәйкес ұғымның ережесін алуға болады. Мысалы, бір айнымалысы бар теңсіздіктер жүйесінің шешімін анықтау негізінде: "Бір айнымалысы бар теңсіздіктер жүйесінің шешімі деп - жүйенің әрбір теңсіздігіне қойғанда дұрыс болатын айнымаланың мәнін атайды", - теңсіздіктер жүйесін шешудің осындай бағдарламасын құруға болады:
1 қадам - әрбір теңсіздік айнымалы үшін сандық аралықты оның шешімін алып, жүйенің әрбір теңсіздігін шешу;
2 қадам - алынған санды аралықтардың ортақ бөлігін табу. Дәл осындай анықтамалар , теоремалардың , формулалардың көмегімен қиындығы жоғары есептерді шағаруда қолданудың маңыздылығы жоғары болып табылады.
Математиканы оқытуда стандартты емес есептерді шығаруға үйрету білім алушыларға негізгі математикалық ұғымдарды қалыптастырып, олардың бағдарламада анықталған теориялық білімді терең меңгеруіне маңызды орын алады.қиындығы жоғары есептер білім алушыларға жаңа білімді қалыптастыратын және бұрыннан бар білімдерін онан ары дамытуға мүмкіндік беретін материалдар болып табылады. Есеп шығару білім алушылардың ақыл-ойының дамуына игі әсерін тигізеді, себебі ол анализ және синтез, нақтылау және абстракциялау, салыстыру, жалпылау сияқты ойлаумен жүргізілетін кезеңді талап етеді.
Есеп шығара білу - әр адамның математикалық, логикалық, аналитикалық және сын тұрғысынан ойлау қабілетінің даму көрсеткіші. Оқу үрдісінде стандартты емес тапсырмаларды пайдалану проблемасымен көптеген ғалымдар біздің елде де, шетелде де айналысады. Мұндай ғалымдардың бірі- Д.Пойя. Өзінің "тапсырманы қалай шешу керек" кітабында ол кез келген математикалық, соның ішінде стандартты емес есептерді шешу проблемаларына психологиялық-педагогикалық талдау жасайды. Оның кітабының соңында кесте бар, оның көмегімен мұғалім тапсырманы өз бетінше орындауға кірісуге немесе одан әрі жалғастыру үшін оқушыға жібере алады. Шын мәнінде, осы кестелер өз бетімен жұмыс істеуге мүмкіндік беретін құрал болып табылады. Кестелер ұсынымдар немесе жетекші сұрақтар түрінде көрсетілетін стереотиптік басшылық принциптердің күрделі жүйесін білдіреді.
Математиканы оқытуда есептерді шеше білу дағдысын қалыптастыру және оны жалпы түрде дамыту аса маңызды мәселелердің бірі болып табылады. Есептер шешу туралы жалпы-білік дағдылар әдетте көптеген есептерді шешіп жаттығу арқылы қалыптасады. Шешу жолы беймәлім, әр түрлі тероиялық фактілерді байланыстыруды қажет ететін, барлық оқушы шығара алмайтын есептер жиы кездеседі. Сондықтан оқушыларды да кез келген матиматикалық есепті шешудің жалпы тәсілдерімен қаруландыру керек. Практикадан байқалатыны көбінесе геометриялық, пропорцияға байланысты экономикалық , дирхиле приципне байланыты логикалық, математикадағы төрт шаманың бір трапецияда таблуы, геометриялық теңсіздіктер, сандардың бөлінгіштігіне есептер қызықты әрі әр түрлі тәсілдермен логикалық тұрғыда көбірек ойлануды қажетсінеді.
1.2 Стандартты емес есептердің түрлері
Стандартты емес арифметикалық есептер-бұл сандардың үстінен арифметикалық әрекеттердің көмегімен кейбір шаманың мәнін табу талап етілетін және мектеп математика курсында шешімді анықтайтын жалпы ережелер жоқ мәтіндік есептер. Е. Е. Останина мынадай есептер шешуге көмектесетін тәсілдер немесе тәсілдер бойынша осындай есептердің түрлерін бөледі: суретті немесе сызбаны құру, қосалқы элементті (бөлікті) енгізу, таңдау тәсілін пайдалану, ол таныс және түсінікті болу үшін есептерді қайта қалыптастыру, есептің шарты немесе сұрағына бөлу және есептерді бөліктер бойынша шешу, "соңынан" бастап есептерді шешу.

Комбинаторлық есептер - бұл барлық ықтимал нұсқаларды қайта Таңдауды немесе олардың санын есептеуді талап ететін есептер[2]. Комбинаторлық есептер қосындылар, туындылар ережесі және комбинация түрлері: комбинация, орналастыру, орнын ауыстыру. Комбинаторлық есептерді шешу әдістері: комбинацияның әртүрлі түрлерінің санын есептеу үшін ережелер мен формулалардың көмегімен ретсіз және жүйелі (таңдалған алгоритмнің көмегімен, кестелерді, графтарды және мүмкін нұсқалардың ағаш графтарының түрлерін құру көмегімен) аралықтар.
Мектепте комбинаторлық-ықтималдық ұғымдармен танысу мынадай ерекшеліктерге ие:
1) оқушылардың кездейсоқ үдерістерді түсінуінде бейсаналық және интуитивті;
2) оқушылардың өмірлік тәжірибесіне сүйену қажеттілігі;
3) мектепте алған білімдермен, іскерліктермен және дағдылармен тығыз байланыста тиісті когнитивтік құрылымдарды қалыптастыру ұзақтығы.
Білім алушылардың математикалық даму дәрежесі олардың есеп шығара білуінен анық байқалады. Есеп дегеніміздің өзі - әрбір мектептегі білім алушының ақыл-ойын ұштаудың негізгі құралы. Әдеттен тыс, қызықты есептердің шешімін табу балалардың математикалық шығармашылығында маңызды орын алады. Ең әуелі, есеп шығаруды үйрену - оның шешімін табу екенін есте ұстаған жөн.
Кез келген қиын есепті шығару білім алушыдан үлкен еңбекті, ерен күші мен табандылықты талап етеді. Бұл қасиеттер баланың есепке ынтасы оянғанда күшейе түседі. Қызықты есептер ақыл-ой энергиясын қозғалысқа келтіретіндіктен, оларды шешу оңайға түседі. Міне, сондықтан мүғалім оқушылар қызығып, өз еріктерімен шығаратын есептерді таңдап алуы қажет.
Оқушылардың математикалық қабілеттерін дамыту және математикаға ынтасын тәрбиелеуде әзіл-есептер мен математикалық ребустарды пайдалану тиімді. Есепті шығара алатынына оқушының сенімді болуы да табысқа жеткізетін маңызды фактордың бірі. Есеп шамадан тыс қиын болса мектеп оқушысының шарасы таусылып, ойлау нәтижелігі төмендейді, әрі қарай үйренуіне нұқсан келеді. Мұғалім есептерді ептілікпен таңдау арқылы өз шәкірттерінің сенім күшін, жігері мен қызығуын, оның шешімін табуға ұмтылуы қолдан келетініне сену жетістікке жету үшін қажет алғы шарттар. Әрбір есепті шығару процесіндегі төрт сатыны ажырата білетін дұрыс: 1) есептің шартын ұғу; 2) жоспар құру; 3) жоспарды жүзеге асыру; 4) артқа көз салу, яғни табылған шешімді пысықтап үйрену.
Білім алушылардың меңгерген материалын шығармашылықпен ұғынуы және жаңа іс-әрекет тәсілдерінің туындап, дамуы ойлаудың мынадай үш құрамының болуына байланысты: 1) анализ және синтез, салыстыру, аналогия, классификация тәрізді қарапайым ойлау операцияларының жоғары деңгейде қалыптасуы; 2) көп болжам, шешімдер варианттары мен тосын идеялар ұсынудан көрінетін ойлау белсенділігінің плюралистігінің жоғары денгейі; 3) өзіндік ойлау әдісінен көрінетін ұйымдасқандық пен мақсаткерліктің жоғары деңгейі.
Аталған ойлау сапаларының қалыптасуы білім алушының шығармашылық тұлғасын дамытуға оқу материалын игерудегі қиындықтарды жеңуге жол ашады. Мұның мәні мынада, білім алушы білім мен іс - әрекеттің теориялық негізделген тәсілдерін біліп, оны тосын жағдайларда қолданады немесе қойылған мәселені шешуге жаңа тәсілдерді өз бетінше таба алады. Мұғалімнің міндеті осы айтылған ойлау компоненттерін қалыптастыра білу болмақ. Ал оның кілті - шығармашылық есеп шығару. Білім алушылардың шығармашылық есептерді шығаруы олардың білім, білік, дағдысы арқылы іске асады. Сонымен қатар, сабақта жоғары белсенді ойлау әрекетінің сақталуында мотивация, білім алушының өз ісіне ынтасы рөл атқарады. Демек, білім алушы шығармашылық іс-әрекетке бейімдейтін, ақыл-ойын, дамытатын құрал деп қызықты есептерді (долбарлау есептері, басқатырғылар, логикалық есептер) айтуға болады. Оларды шығармашылық іс-әрекетті жетілдіріп, ақыл-ойды жаттықтыратын көмекші, қосымша жол ретінде ұғымды пайдалану мүмкіндігі мол. Мұндай материалдар сан алуан болғанымен, төмендегідей ортақ қасиеттері бар.
1) Қызықты есептердін шешу жолы белгісіз. Олардың шешіміне жету ойдың броундық қозғалысы тәрізді, яғни байқап көру, қателесу әдісімен іске асады. Байқап көру арқылы іздену жеке жағдайларда негізгі шешімге бастайтын тізгінді қолға ұстатады;
2) қызықты есептер білім алушының пәнге қызығуына, белсенділігіне негіз болады. Есеп сюжетінің шешілу жолының әдеттен тыс болуы бала көңіліне әсер етіп, қайткенде де оны шығаруға итермелейді;
3) қызықты есептер ойлау заңдылықтарын білуге негізделіп жасалады.
Міне, осындай есеп түрлерін жүйелі түрде қолдану аталған ойлау операцяларын дамытуға, балалардың математакалық түсініктерін қалыптастыруға жағдай жасайды. Қызықты есептерді шығару көбінесе байқап көріп іздену процесімен жүреді. Ойша болжай білу балалардың бойындағы тапқырлық пен аңғарымпаздықты байқатады. Тапқырлық - шығармашылықтың ерекше көрінісі, ол талдау, салыстыру, жалпылау, байланыстарды анықтау, ұқсастыру, тұжырымдау ой корыту нәтижесінде байқалады. Ал аңғарымпаздықтың белгісі нақты жағдайды ой елегінен өткізіп, өзара байланыстарды анықтай білу, соның негізінде есеп шығарушы бір тұжырымға келіп, ойын топтайды. Аңғарымпаздық өз білімін кәдеге асыра білудің көрсеткіші болып табылады. Қызықты есептердің шешімін болжауға қол жеткізетін тапқырлық пен аңғарымпаздық ғайыптан келер нәрсе емес. Мұндай ақыл-ой әрекетінің жетістігін оқыту процесінде дамытуға болады, әрі солай ету қажет.
Кез келген жағдайда есептің шешімін болжау үшін мұқият талдау жасалады: есептің басты қасиеттерін, фигуралардың кеңістіктегі орналасуы мен топтасуын, олардың ерекшелігін, ұқсас белгілерін ажыратып алу, т.б. Алайда, қызықты есептерді шығару үшін байқау және қателесу әдісі оншалық сенімді әрі жан-жақты емес. Неғұрлым тиімді әдіс -- балаларды ақыл-ой әрекетінің анализ және синтез, салыстыру, ұқсастыру, дәрежелеу тәрізді маңызды тәсілдермен қаруландыру.
1) Cандық байланыстарға арналған есептер

Белгілі бір ортақ қасиеттері бар заттарды санау үшін қолданылатын сандар натурал сандар деп аталады. N =
Бір - ең кіші натурал сан, ал ең үлкен натурал сан жоқ. Кез келген натурал сан 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 цифрларының көмегімен жазылады. Мысалы, 23041 және т.с.с.
Натурал сандарды жазуда қолданылатын цифрлар оңнан солға қарай есептелгенде, тұрған орнына байланысты осы санның құрамында неше бірлік, неше ондық , неше жүздік, неше мыңдық, неше он мыңдық т.с.с. бар екенін көрсетеді. Мысалы, 5793 санында 3 бірлік, 9 ондық , 7 жүздік және 5 мыңдық бар. Жалпы оң жағынан санағанда k- шы орында тұрған цифр осы сонда неше 10к-1 разрядты сан бар екендігін білдіреді. Яғни n таңбалы a саның мынадай түрде жазуға болады :
(4)
Мұнда а натурал саны цифрларының көмегі арқылы жазылған. Оны қысқаша былай белгілейді: . Мысалы, .
Натурал сандарды қосу және көбейту амалдары үшін ауыстырымдылық, терімділік және үлестірімділік заңдары орындалады.
Сандық байланыстарға арналған есептерді шешу кезінде келесі ережелер қолданылады:
A=an-1∙10n-1+an-1∙10n-1+...+a1∙10+a 0,
A=an-1∙10n-1+an-1∙10n-1+...+a1∙10+a 0,
1) егер А натурал саны n таңбалы болса, онда

болады, мұндағы a0,a1,a2,...,an-1a0,a1,a2,...,an-1- А санындағы сәйкесінше бірліктер, ондықтар, жүздіктер, ... саны;
егер А натурал санын В натурал санына бөлгенде q бөлінді және r (r B) қалдық шығатын болса, онда A = Bq + r болады.
A=an-1∙10n-1+an-1∙10n-1+...+a1∙10+a 0,
A=an-1∙10n-1+an-1∙10n-1+...+a1∙10+a 0,
Жоғардығы формуланың қолдануына есептер қарастырсақ:
Екітаңбалы санның бірлігі ондығынан 2-ге артық, ал ізделінді сан мен оның цифрларының қосындысының көбейтіндісі 144-ке тең. Осы санды табыңдар.
(x - 2)10 + x = 11x - 20.

(x - 2)10 + x = 11x - 20.

Шешуі. Ізделінді санда х бірлігі болсын.Сонда оның (x - 2) ондығы болады. Демек, ізделінді сан келесі түрде болады: Ізделінді санның цифрларының қосындысы: (x - 2) + x = 2x - 2.
Сонымен, келесі теңдеуді құрастырамыз: (11x - 20)(2x - 2) = 144
теңдеуді шешіп, түбірлерін табамыз:х1=4 х1=4 жәнех2=1311.
х және (x - 2) - санның цифрлары болғандықтан, x ∈ N
0=x=90=x-2=9
0=x=90=x-2=9
х2=1311 Бұл шарттарды х-тің бір ғана мәні қағаттандырады:
x = 4. Сонда ізделінді сан 11 · 4 - 20 = 24 болады. Жауабы: 24.
Егер екі екітаңбалы санның біріншісіне екіншісін оң жағынан тіркеп жазса және тағы 0 цифры жазылса, онда пайда болған бестаңбалы санды екінші санның квадратына бөлгенде бөлінді 39, қалдығы 575 болады; егер бірінші санға оң жағынан тіркеп екінші санды жазып, құрылған жаңа саннан екінші санға оң жағынан тіркеп бірінші сан жазылған санды азайтсақ 1287 шығады. Осы екітаңбалы сандарды табыңдар.
Шешуі. x - бірінші сан және y - екінші сан болсын. у санын х санына оң жағынан тіркеп жазсақ, x · 100 + y төрттаңбалы саны шығады және осы санға оң жағынан тағы 0 цифры жазылса, онда келесі сан пайда болады: (x · 100 + y) · 10. Осы санды y[2] y2санына бөлсек, онда бөлінді 39, қалдығы 575 болады,
яғни (x · 100 + y) · 10 = y[2]y2 · 39 +575.
Енді x бірінші санын y екінші санының оң жағына тіркеп жазсақ, y · 100 + x төрттаңбалы саны шығады. Сонымен, екінші теңдеуді аламыз:
(x · 100 + y) - (y · 100 + x) = 1287.
Теңдеулер жүйесі келесі түрде болады:
(x · 100 + y) · 10 = y2 · 39 +575. (x · 100 + y) - (y · 100 + x) = 1287.--1000x + 10y = 39y2+575. 99x-99y= 1287.
Бұл жүйенің екі шешімі болады: (48; 35) және15236;-35539 Жауабы: 48 және 35.

2)Сандардың бөлінгіштік белгілері
Егер а және в сандары үшін с саны табылып, а = вс теңдігі орындалса, онда а санын в санына қалдықсыз бөлінеді деп аталады.
Мысалы, а:в =с. Мұнда а - бөлінгіш, в - бөлгіш, ал с бөлінді.
Кейбір сандардың бөлінгіштік белгілерін келтірейік:
1) 2-ге бөлінгіштік белгісі. Егер санның соңғы цифры нөл немесе жұп сан болса, онда бұл сан 2-ге қалдықсыз бөлінеді.
2) 4-ке бөлінгіштік белгісі. Егер санның соңғы екі цифры нөл болса немесе осы соңғы екі цифрдан құрылған екі таңбалы сан 4-ке бөлінсе, онда бұл сан 4-ке қалдықсыз бөлінеді.
3)5-ке бөлінгіштік белгісі. Егер сан 0 немесе 5 цифрымен аяқталса, онда бұл сан 5-ке қалдықсыз бөлінеді.
4)3 пен 9-ға бөлінгіштік белгісі. Егер санның цифрларының қосындысы 3-ке (9-ға) бөлінсе, онда бұл сан 3-ке (9-ға) қалдықсыз бөлінеді.
5) 6-ға бөлінгіштік белгісі. 3-ке бөлінетін жұп сандар 6-ға қалдықсыз бөлінеді.
6) 11-ге бөлінгіштік белгісі. Егер санның жазылуындағы тақ орындағы цифрлардың қосындысы мен оның жұп орындарындағы цифрлардың қосындысының айырмасы нөлге тең немесе 11-ге бөлінетін болса, онда бұл сан 11-ге қалдықсыз бөлінеді.
4-ші және 6-шы белгілердің дәлелдеуін көрсетейік.
4- белгінің дәлелдеуі. = саны берілсін. Мұндағы 10=9+1, 100=99+1, 1000=999+1,... екендігін ескерсек,
теңдігін аламыз. Мұнда тоғыздықтары бар қосылғыштардың барлығы 9-ға ( 3-ке) бөлінеді. Яғни қосындысыда 3-ке немесе 9-ға бөлінсе жеткілікті.
6- белгінің дәлелдеуі. Анықтық үшін берілген санды жұп таңбалы сан деп алайық:
Осыдан берілген сан 11-ге бөліну үшін: айырмасы 11-ге бөлінуі керек немесе 0-ге тең болуы керек.
Мысалы, санының 11-ге бөлінетіндігін дәлелдеу керек:
Соңғы сан 11-ге бөлінеді.
6-белгі бойынша болғандықтан саны 11-ге бөлінеді.
3) Теңдеулер мен теңсіздіктер
Төмендегі бірнеше мысал арқылы стандартты емес есептерді шығаруды бұрынғы шығарылған есептерге келтіруді көрсетейік.
1-мысал. Теңсіздікті шешіңіздер:
Шешуі: Берілген теңсіздікті оң бөлігі ноль болатын теңсіздікпен ауыстырамыз.
Бұл тәсіл, яғни теңсіздікті түрлендіру арқылы, оның бір жақ бөлігін нольге келтіріп шығару, теңсіздіктің бір жағы сан немесе өрнек болып келген теңсіздіктерді шешуден көп жеңіл. Егер теңсіздіктің оң жақ бөлігінде ноль болса, онда сол жақ бөлігінің оң немесе теріс екендігін дәлелдеу керек. Сондықтан 3 соsх-ті сол жаққа көшіреміз, яғни 2+ соз 2х- 3 соз х 0
Мұндағы тригонометриялық функциялардың аргументтері бірдей болса, онда теңсіздік ықшамдалар еді. Сондықтан қос бұрыштың формуласын қолдана отырып, теңсіздікті мынадай түрге келтіреміз: . Енді белгілеп, алгебралық квадрат теңсіздікті аламыз да, оған квадрат үшмүшеліктің қасиетін пайдалана отырып екендігін көреміз. Яғни теңсіздіктің шешімі болады, енді қайтадан t-ның орнына қойсақ тригонометриялық теңсіздікке келеміз. Бұл қарапайым теңсіздік, шешімі
2-мысал. Төмендегі теңдеуінің графигін салыңыздар.
1-тәсіл. Берілген тендеудің графигін салуды, бұрыннан бізге таныс теңдеудің графигін салуға келтіруге тырысайық.
Тәуелділік тендеуін өзімізге таныс түрде жазайық: .
Егер біз теңдеуінің графигін сала алсақ, бұл теңдеудің графигін салу жеңілденер еді.
Ал бұл теңдеудің графигін теңдеуінің графигін ОХ -- осі бойымен оң жаққа 1 бірлікке параллель жылжыту арқылы алуға болады. Яғни енді біз теңдеуінің графигін салуға көшеміз.
Абсолют шаманың анықтамасын пайдалана отырып, есепті (;0) және (0;) облыстарында қарастырамыз. Сонда
онда
онда
y
x
y=2-x
y
x
y=2-x
1-сурет
Осы теңдеудің графигін ОХ -- бойымен оңға бір бірлікке параллель көшіру арқылы, теңдеуінің графигін аламыз.
x
y=2-x-1
y
x
y=2-x-1
y

2-сурет
Енді теңдеуінің графигін салып көрейік. Егер болса, теңдеу мағынасын жояды, сондыктан оң мәндер кабыдайтын облыста карастырамыз, х [-1;3] және егер у0, теңдеу түріне, ал у0 болса түріне келеді.
x
y=2-x-1
y
-1
3
x
y=2-x-1
y
-1
3
тәуелділігінің графигі 3-суреттегідей болады.

3 -сурет
2-тәсіл.
(1) тәуелділігінің графигін, (2) тәуелділігінің графигін ОХ бойымен оңға бір бірлікке параллель көшіру арқылы салуға болатынын байқаймыз. Сонымен қатар (2) теңдеуде х-ті - х пен, у - ті - у ауыстырғанда ол өзгермейді, яғни оның графигі координаттар осіне карағанда симметриялы болады. Бұдан біз графикті координаттық бір ширекте салсақ та жеткілікті, мысалы бірінші ширекте. Онда тендеуіміз х+у = 2 келеді.
Бұл тәуелділіктің графигі 4-суретте көрсетілген.
x
y
x
y

4-сурет
y
x
x+y=2
y
x
x+y=2
Енді бұл графиктің ОХ және ОУ осіне қарағанда симметриялы екенін еске түсіре отырып келесі графикті саламыз.

5-сурет
Ал (1) тәуелділіктің графигін салу үшін, графикті оңға ОХ бойымен бір бірлікке параллель көшіреміз. Яғни ізделінді графикті аламыз. (6-сурет).

x
x-1+y=2
y
x
x-1+y=2
y

6-сурет.
Біз екі тәсіл арқылы стандартты емес есепті бұрынғы шығарылған есепке келтірдік. 1-тәсілде біртіндеп түрлендіру арқылы берілген есепті бұрын шығарылған стандартты түрдегі есепке келтірдік.
Ал 2-тәсіл арқылы біз есептің шартын тиянақты түрде талдау барысында бұрын шығарылған есепке келдік.
3-мысал. Тендеулер жүйесін шешіңдер:

Бұл теңдеулер жүйесі түріне карасақ біздің шығарып жүрген жүйелеріміз сияқты. Тереңірек үңілсек шығару тәсілі бізге таныс емес екендігін байқаймыз.
Есептің шартын тиянақты түрде талдай бастасақ 1-теңдеудің сол жағы негізі 3-ке тең логарифмдердің айырымы екендігін байқаймыз да, оң жағын да негізі 3-ке тең логарифмге келтірсек деген ой туады.
Ал 2-тендеуді талдау барысында 48-ді теңдіктің негізі 4 болғандығы логарифмдік көрсетеіш түріне келтірсек, онда теңдеулер жүйесі төмендегідей түрге келеді:

Енді 2-ні -мен ауыстырсақ, онда тендеулер жүйесі өзіміз шығарып жүрген стандартты түрдегі жүйеге келеді:

Логарифмдердің касиетін пайдалана отырып алгебралық жүйеге келеміз.

Жүйені косу немесе алмастыру тәсілін колдана отырып шешеміз х=42, у=39 болады. Шешімді тексеріп, жауабын жазамыз.
4) Ирроционалды лагорифмдік теңдеулер:
а) lg3 + 0,5lg(x - 28) = lg тендеуін шешу
Шешуі:
lg3 + 0,5lg(x - 28) = lg,
lg(3 = lg,
анықталу обылысын ескергенде, берілген теңдеу:

жүйесіне тең.
Жауабы: 32,75
б) теңдеуін шешу
Шешуі:

Жауабы: -135; - 2; 3.
Иррационалды теңсіздіктер. Теңсіздік иррационалды деп аталады, егер оның белгісізі түбір белгісінің астына кірсе.
түріндегі иррационалды теңсіздік
(5)
теңсіздіктер жүйесіне тең.
түріндегі иррационалды теңсіздік:
және (6)
екі ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.