Ақпарат саны

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

М. Х. Дулати атындағы Тараз өңірлік университеті

Ақпараттық технологиялар, автоматика және телекоммуникация факультеті

Автоматика және телекоммуникация кафедрасы

КУРСТЫҚ ЖҰМЫС

Қолданбалы ақпараттық теориясы пәні бойынша

Тақырыбы: Сигналдар мен олардың математикалық үлгілері

Білімгер:Тоқтасынов Әубәкір Тобы: 6В07122-19/4

Жетекші:

/қызметі/ /аты-жөні/

Қорғауға жіберілді: «»20ж.

/қолы/

Жұмыс қорғалды: «»20ж. Бағасы:

/жазбаша/

Комиссия мүшелері :

/аты-жөні/ /қолы/

Тараз 2021

Мазмұны

Кіріспе

Сигналдардың математикалық модельдері

1. 1 Сигнал және оның моделі түсініктері

1. 2 Детерминирленген сигналдарды беру формалары

1. 3 Детерминирленген сигналдардың математикалық модельдері

1. 4 Сигналды берудің уақыттық формасы

Сигналдың моделі ретіндегі кездейсоқ процессСигналдың моделі ретіндегі кездейсоқ процессКездейсоқ процестің ықтималдық сипаттамалары

Кванттау және дискреттеуҮздіксіз мәліметтер. Кванттау және дискреттеуДискреттеу есебінің жалпы қойылымыТаңдау көмегімен жасалатын дискреттеу әдістері

Ақпарат саны

Мәліметтер көзінің және байланыс каналының ақпараттық сипаттамалары

Қорытынды

Пайдаланылған әдебиеттер

Кіріспе

Ақпарат алмасуды тиімді ұйымдастыру адамдардың ойдағыдай машықтану іс-әрекеттерінің шарты ретінде үлкен мәнге ие болуда. Қазіргі кезеңдегі қоғамның жұмыс істеуіне қажетті ақпарат көлемі өндірістік потенциалға пропорционал өсуде. Ақпаратпен қамтамасыз ету мәселелерімен айналысатын жұмыс күшінің үлесі тікелей өндірістегі жұмыс күшінен арта түсуде. Сондықтан, мұндай жағдайларда қатарында ақпарат теориясы да бар ақпараттық процестердің өту заңдылықтарын және құрылымын зерттейтін ғылымдар өте өзекті мәселе болып отыр.

Ақпарат материя және энергиямен қатар бастапқы түсінік болып табылады және қатаң мағынада анықтала алмайды. Оның тек негізгі қасиеттерін айтуға болады, мысалы:

а) ақпарат қоршаған орта туралы мәліметтерден тұрады;

ә) ақпарат материалды емес, бірақ ол дискретті таңбалар немесе бастапқы сигналдар түрінде болады;

б) таңбалар және бастапқы сигналдар танитын алушыға ғана ақпарат әкеледі.

Сонымен қатар ақпарат сөзі тек қана ғылыми еңбектерде ғана емес күнделікті өмірде де жиі кездеседі және әрбір адамға интуитивті түсінікті болып табылады. Бұл кезде қысаң практикалық мағынада ақпарат ретінде әдетте сақтау, тасымалдау және түрлендіру нысандары болатын қоршаған орта туралы мәліметтер жиынтығын түсінеді.

Тізбекте ұйымдастырылған белгілер немесе бастапқы сигналдар олардың шынайы уақыт нысандарын қайталайтындықтан емес, белгілер мен нысандардың арасындағы бір мағыналы байланыс туралы қоғамдық келісімділік бойынша ақпарат тасиды, мысалы, заттар және оларды белгілейтін сөздер. Сонымен қатар, бастапқы сигналдар шынайы өмірдің табиғи заңдарымен тууы мүмкін, мысалы, термопараның шығысындағы температура әсерімен болған кернеу.

Белгілер немесе сигналдардың шынайы өмір нысандарымен бір мағыналы байланысына негізделген ақпарат семантикалық немесе мағыналық деп аталады. Белгілердің ұласу сипатына (реті және өзара байланысы) негізделген ақпарат синтактикалық деп аталады. Белгілер туралы жалпы ғылымда (семиотика) аталғандардан басқа ақпараттың сигматикалық және прагматикалық тұрғыларын да ерекшелейді. Бірінші жағдайда шынайы өмірдің нысандарын белгілеу үшін белгілерді таңдау, ал екінші жағдайда қойылған мақсаттарға жету үшін ақпараттың құндылық мәселесі зерттеледі. Ең көп практикалық қызығушылық ақпараттың мағыналық, семантикалық және прагматикалық тұрғыларында болатындығы анық. Қазіргі кезеңге дейін ақпараттың құндылық және пайдалық өлшемдерінің сандық критерийлері анықталмаған. Ақпарат теориясы курсында негізгі жұмыс істеу көрсеткіштері мүмкін болатын шекке жақын болатын байланыс жүйелерін құрудың теориялық негіздерін жасауға қатысты синтактикалық деңгейдің мәселелері зерттеледі. Басқаша айтқанда, алушыға белгілер жиынтығы ретіндегі ақпаратты жеткізу сұрақтары қаралады. Бұл кезде оның мағыналық және прагматикалық мазмұны еленбейді.

1 тарау. Сигналдардың математикалық модельдері

1. 1 Сигнал және оның моделі түсініктері

Кең мағынада сигнал деп ақпараттың материалды тасушысын түсінеміз. Сигналдарға табиғи және белгілі мақсатпен құрылатын сигналдарды жатқызуға болады. Табиғи сигналдарға жарық сигналдарын жатқызуға болады. Арнайы жасалатын сигналдарға нысанның немесе процестің өзгеруі туралы ақпаратты алуға арналған сигналдарды жатқызуға болады.

Сигналдың материалдық негізін ақпараттың тасушысы деп аталатын физикалық нысан немесе процесс құрады. Тасушы модуляция кезінде сигналға айналады.

Берілетін мәліметтерге сәйкес уақыт бойынша өзгеретін тасушының параметрлері информативті деп аталады. Тасушы ретінде тербелістер қолданылады. Егер болса бірінші ақпараттық параметр деңгей болады. Гармоникалық электрлік тербелістердің параметрлері: амплитуда, жиілік, фаза. Тербелістер детерминирленген және кездейсоқ деп бөлінеді. Детерминирленген тербелістер әрбір уақыт кезеңінде дәл анықталған. Кездейсоқ тербелістердің кейбір параметрлерін дәл болжау мүмкін емес. Олар ақпарат таситын сигналдар ретінде немесе бөгеуілдер ретінде қарастырыла алады.

Байланыс каналдарының, сигналдардың және бөгеуілдердің жалпы қасиеттерін зерттегенде олардың физикалық табиғатын, мағынасын және міндетін модельдермен ауыстырамыз. Модель - шешілетін есеп тұрғысынан қарағанда айтарлықтай факторларды бейнелейтін нысанды, процесті немесе болмысты суреттеу әдісі. Математикалық модельдеу әртүрлі көрсеткіштерді анықтайтын әдіске байланысты әртүрлі әдістермен іске асырылады. Фундаменталды зерттеулер аналитикалық модельдеу әдістеріне негізделеді. Мысалы, сигналдың моделі шектелмеген ұзақтығы бар (синусоидалар) шексіз функциялар санының қосындысымен беріледі. Мәліметтер көзі әрбір мәліметті белгілі бір ықтималдықпен беретіндіктен информативті параметрдің мәнінің өзгеруін дәл айту мүмкін емес. Демек, сигнал кездейсоқ тербеліс болып табылады және оның аналитикалық моделіықтиалдық сипаттамалармен анықталатын тек қана кездейсоқ процесс болуы мүмкін.

1. 2 Детерминирленген сигналдарды беру формалары

Информативті параметрлердің құрылымына байланысты сигналдар келесілерге бөлінеді:

дискретті (мәндер саны шекті) ;
үздіксіз - (континуум) ;
үздіксіз-дискретті.

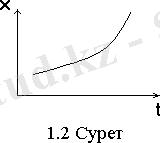
1. 2. 1 Үздіксіз немесе аналогты сигналдар (бұл типті кездейсоқ сигналдар үздіксіз кездейсоқ процестер деп аталады) . Олар уақыттың барлық кезеңдері үшін анықталған және берілген диапазоннан барлық мәндерді қабылдай алады. Сигналдардың пайда болуына себепкер физикалық процестер көбінесе үздіксіз болады. Мұнымен сигналдардың аналогты деп аталатын екінші аты түсіндіріледі.

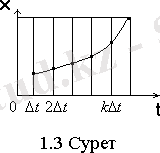
1. 2. 2 Дискреттелген немесе дискретті-үздіксіз сигналдар (бұл типті кездейсоқ сигналдар дискретті уақытты процестер немесе үздіксіз кездейсоқ тізбектер деп аталады) . Олар бөлек уақыт кезеңдерінде ғана анықталған және деңгейдің кез келген мәндерін қабылдай алады. Көршілес санақ арасындағы Δt уақыт интервалы дискреттеу қадамы деп аталады. Мұндай сигналдар уақыт бойынша дискретті деп те аталады

1. 2. 3 Деңгей бойынша дискретті немесе квантталған сигналдар (бұл типті кездейсоқ сигналдар дискретті кездейсоқ процестер деп аталады) . Олар уақыттың барлық кезеңдері үшін анықталған және деңгейдің тек қана рұқсат етілген мәндерін ғана қабылдайды Δx = x _k+1 + x _k .

1. 1. 4 Деңгей және уақыт бойынша дискретті сигналдар (бұл типті кездейсоқ сигналдар дискретті кездейсоқ тізбектер деп аталады) . Олар тек қана уақыттың бөлек рұқсат етілген кезеңдерінде ғана анықталған және тек қана деңгейдің рұқсат етілген мәндерін ғана қабылдайды.

1. 3 Детерминирленген сигналдардың математикалық модельдері

u(t) күрделі сигналы уақыт бойынша инвариантты сызықты жүйелерден өткенде ол 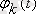салмақталған базисті функциялар қосындысы түрінде беріледі.

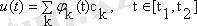(1. 1)

мұндағы - сигналдың бар болу уақыты.

Алынған базисті функциялар жиынында u(t) сигналы толығымен 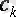өлшеусіз коэффициенттер жиынтығымен анықталады. Сандардың мұндай жиынтығы сигналдардың дискретті спектрі деп аталады.

(1. 1) амалы 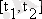интервалында уақыт бойынша шектелмеген сигналдар үшін және шекті ұзақтықты сигналдар үшін де әділ. Бірақ та 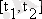интервалынан тыс жатқан шекті ұзақтықты сигнал нөлге тең емес, өйткені ол шартты түрде периодты жалғасады деп есептелетін болса ғана қосынды ретінде беріледі. Сондықтан уақыт бойынша шектелген сигнал үшін кез келген уақыт кезеңінде әділ болатын ұсынысты алу керек болса, келесі интеграл қолданылады

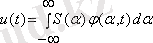(1. 2)

мұндағы 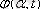- үздіксіз өзгеретін 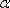параметрімен базисті функция.

Сигналдың үздіксіз (тұтас) спектрі 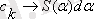спектрлі тығыздығымен беріледі. 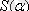- өлшемі 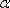кері . Мұнда өлшеусіз коэффициентінің аналогы болып шамасы табылады

Сигналдарды (1. 1) және (1. 2) түрінде беру сигналдардың жалпыланған спектрлі теориясы деп аталады.

Теориялық талдау үшін 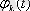қарапайым болуы керек және (1. 1) қатарының тез жинақталуын қамтамасыз етуі керек.

1. 4 Сигналды берудің уақыттық формасы

Сигналды берудің уақыттық формасында бірлік импульсті дельта функциялар қолданылады

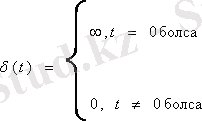(1. 9)

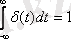, мұндағы 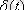координаталар басында 0-ден өзгеше.

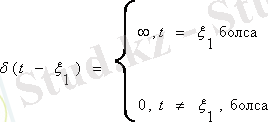
. (1. 10)

(1. 10) көмегімен уақыт кезеңіндегі мәнін беруге болады

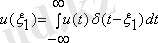, (1. 11)

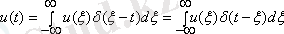. (1. 12)

Кіріс сигналын дельта функциясы түрінде қойып (импульсті өтпелі функция) кіріс сигналының сәйкес мәндеріне тең ауданмен жылжытылған дельта-импульстердің шексіз тізбектеріне реакциялардың суперпозициясы ретінде кіріс сигналына жүйенің реакциясын оңай анықтауға болады

Дельта-функциялар көмегімен тұрақты немесе өзгеретін деңгейлермен идеалды периодты импульстер тізбегін беруге болады. 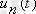- 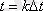нүктелерінде -ға тең, ал басқа жағдайларда нөлге тең функция.

(1. 13)

- импульстердің ұласу периоды.

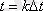уақыты кезеңінде u(t) -ні дельта функцияға көбейту бұл функцияның санағын алуға сәйкес болғандықтан u(t) функциясының бірқалыпты дискреттеу нәтижесін бере алады.

2 тарау. Сигналдың моделі ретіндегі кездейсоқ процесс

2. 1 Сигналдың моделі ретіндегі кездейсоқ процесс

Қарастырылған детерминирленген сигналдардың модельдері белгілі уақыт функциялары болып табылады. Оларды қолдану берілген кіріс сигналдарына белгілі жүйелердің реакциясын анықтаумен байланысты есептерді шығаруға мүмкіндіктер береді. Ақпаратты алу бастапқы жағдайлардың априорлы анықталмағандығын жоюмен байланысты. Сондықтан сигналдардың моделі ретінде кездейсоқ процесс қолданылады. Әрбір алынған детерминирленген функция осы кездейсоқ процестің іске асырылуы ретінде қарастырылады.

Кездейсоқ (стохастикалық) процесс деп әрбір уақыт кезінде мәндері кездейсоқ болатын кездейсоқ уақыт функциясын айтады. Кездейсоқ процестің белгілі бір тәжірибе кезінде тіркелген түрі кездейсоқ процестің іске асырылуы деп аталады.

Кездейсоқ процестерді классификациялаудың негізгі белгілері: жағдайлар белгілері, уақыттық параметр және әрбір уақыт кезеңіндегі 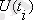кездейсоқ шамалар арасындағы статистикалық байланыстар.

Ерікті уақыт кезеңдерінде өзгере алатын шекті жағдайлар жиынтықты кездейсоқ процесс дискретті деп аталады. Егер, жағдайлардың өзгеруі тек қана шекті немесе саналатын уақыт кезеңдерінде мүмкін болса, онда ол дискретті кездейсоқ тізбек болады.

2. 2 Кездейсоқ процестің ықтималдық сипаттамалары

Анықтама бойынша кездейсоқ процесі 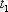… … 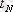уақыт кезеңдерінде алынған = 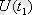, . . . , 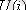= 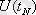, . . . , = тәуелді N кездейсоқ шамалар жүйесімен суреттеледі. N саны шектеусіз өссе, мұндай жүйе кездейсоқ процесіне эквивалентті.

Мұндай жүйенің негізгі сипаттамасы N-өлшемді ықтималдықтар тығыздығы болып табылады. Ол әрбір 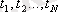уақыт кезеңдеріндегі мәндері сәйкес интервалдарында болатын іске асырылудың ықтималдығын есептеуге мүмкіндік береді. Мұндағы 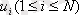- 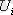кездейсоқ шамасымен қабылданатын мән.

Егер 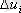аз шама болса, онда

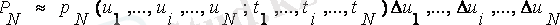
қатынасы әділ.

кездейсоқ процесінің бір өлшемді ықтималдық тығыздығы 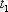уақыт кезеңінде алынған бір кездейсоқ шаманың таралуын сипаттайды.

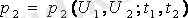екі өлшемді ықтималдық 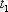және 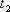өз еркімен алынған уақыт кезеңдерінде кез келген және екі кездейсоқ шаманың бірге іске асырылуының ықтималдығын анықтауға, демек, процестің динамикалық дамуын бағалауға мүмкіндік береді. кездейсоқ процесінің бір өлшемді ықтималдық тығыздығын

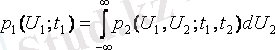(2. 1)

қатынасын қолдану арқылы алуға болады.

кездейсоқ процесінің математикалық күтуі деп кез келген 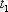аргументінде мүмкін болатын іске асырулар жиыны бойынша 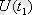кездейсоқ шамасының орта мәніне тең кездейсоқ емес уақыт функциясын айтады:

. (2. 2)

Әрбір 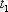үшін 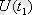процесінің кездейсоқ мәндерінің өзінің орта мәнінен шашырау дәрежесі 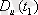дисперсиямен сипатталады

(2. 3)

мұндағы - 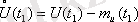- орталықтанған кездейсоқ шама.

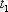әрбір уақыт кезеңінде 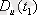дисперсиясы 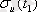орта квадратты ауытқудың квадратына тең

. (2. 4)

Кездейсоқ процестердің бірдей математикалық күтулері және дисперсиялары болуы мүмкін, бірақ уақыт бойынша өздерінің мәндерінің өзгеруімен ерекшеленуі мүмкін.

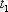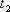Өз еркімен алынған және уақыт кезеңдерінде 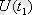процесінің лездік мәндерінің статистикалық байланыстарын анықтау үшін автокорреляциялы немесе корреляциялы деп аталатын кездейсоқ емес аргументтер функциясы қолданылады.

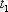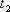және белгілі бір аргументтерде ол процестің 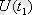және 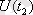корреляциялық кезең мәндеріне тең

. (2. 5)

Екі өлшемді ықтималдық тығыздығы арқылы (2. 5) амалы былайша жазылады

(2. 6)

Бұл формула аргументтерге қатысты симметриялы болуына байланысты

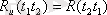(2. 7)

қатынасы әділ.

Әртүрлі кездейсоқ процестерді салыстыру үшін корреляциялық функцияның орнына нормаланған автокорреляция функциясын қолданған ыңғайлы

, (2. 8)

(2. 3) және (2. 4) салыстырса өз еркімен алынған 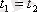кезінде автокорреляциялы функция дисперсияға айналады

, (2. 9)

ал нормаланған автокорреляция функциясы бірге тең

. (2. 10)

Демек, кездейсоқ процестің дисперсиясын автокорреляциялық функцияның дербес мәні ретінде қарастыруға болады.

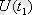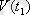Осылайша екі және кездейсоқ процестерінің арасындағы байланыс өлшемдері қойылады. Ол өзара корреляция функциясы деп аталады

. (2. 11)

3 тарау. Кванттау және дискреттеу

3 . 1 Үздіксіз мәліметтер. Кванттау және дискреттеу

Бұл тарауда әрбір уақыт кезеңінде кездейсоқ түрде шексіз мүмкін болатын жағдайлар жиынтығынан бір жағдай қабылдай алатын үздіксіз мәліметтер көзін қарастыратын боламыз. Үздіксіз мәлімет деп көздің жағдайына бір мағыналы сәйкес келетін үздіксіз кездейсоқ шаманы түсінетін боламыз. Мұндай мәліметті ықтималдықты суреттеу толығымен оның таралу тығыздығымен беріледі. Уақыт бойынша өзгеру сипатына байланысты мәліметтер үздіксіз кездейсоқ процестер немесе кездейсоқ тізбектер деп аталатын дискретті уақытты процестер болады. Байланыс каналы бойынша үздіксіз мәліметтерді тасымалдауды ұйымдастырудың екі жолы бар:

а) үздіксіз мәліметтерді дискреттіге түрлендіру және оларды дискретті каналдар бойынша тасымалдау;
ә) үздіксіз каналдар бойынша тасымалдау.

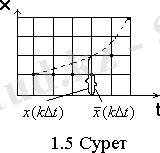
Ең алдымен Х үздіксіз кездейсоқ шамасының санақтар жиынтығымен берілетін дискретті уақытты X(kΔt) процесі болатын үздіксіз мәліметті қарастырайық. Мұндай процестің мүмкін болатын іске асырылуының бірі 3. 1 суретте көрсетілген. Процестің барлық мүмкін болатын (немесе ең болмағанда ең ықтималдықтылары) санақтарының мәндері x _min -нан x _max -ға дейінгі диапазонда орналасқан делік. Бұл диапазонды интервалдарының шекті санына бөлейік

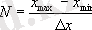(3. 1)

және бұл интервалдардың х _к-1 , х _к , х _к+1 және т. с. с шекараларын санақ деңгейлерін процестің рұқсат етілген мәндері деп есептейміз. Бұл кезде рұқсат етілген деңгейлер саны

N _y =N-1. (3. 2)

3. 1 Сурет

Санақтың өзінің мәнін жақын рұқсат етілген деңгейге дөңгелектеу процедурасы кванттау немесе мән (деңгей) бойынша дискреттеу деп аталады (сигналдың дөңгелектенген мәндері суретте дөңгелекшелермен көрсетілген) . Кванттау операциясынан кейін Х үздіксіз кездейсоқ шамасы мүмкін мәндердің шекті саны бар дискреттіге айналады, ал үздіксіз мәлімет - N _у алфавит көлемімен элементарлы дискретті мәліметтер көзінің тізбегіне айналады . Кванттау операциясы анықтамасынан шығатындай, оған кванттау қателігі бар болғандықтан ақпараттың жоғалуы тән. Қателік мәнін (демек оның әсерінен жоғалатын ақпарат санын) N _у жеткілікті санын алу арқылы азайтуға болады ( кванттау қадамын сәйкес азайту салдарынан) .
Үздіксіз уақытты процестермен суреттелетін үздіксіз мәліметтердің басқа түрінің x(t) іске асырылуы 3. 2 суретте көрсетілген:

3. 2 Сурет

Процесс мәндерінің барлық жиынтығын 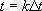белгілі бір рұқсат етілген уақыт кезеңдерінде оның лездік мәндер жиынтығымен ауыстыру дискреттеу деп аталады. Үздіксіз мәліметтерді тасымалдау және түрлендіру процестері үшін дискреттеу маңызды болғандықтан оны толығырақ қарастырайық.

3. 2 Дискреттеу есебінің жалпы қойылымы

Т интервалында u(t) үздіксіз сигналын 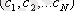координаталарының жиынтығы ретінде беру

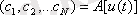(3. 3)

деп жазылуы мүмкін, мұндағы А - дискреттеуші деп аталатын құрылғымен іске асырылатын сигналды берудің дискретті операторы. Осылайша, бастапқы сигналды қателігімен беретін u ^* (t) үздіксіз (қалпына келтіретін) функциясының 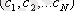координаталар жиынтығы бойынша қалпына келтіру операциясын да жазуға болады

(3. 4)

мұндағы В - сигналды қалпына келтіру құрылғысымен іске асырылатын қалпына келтіру операторы.

Техникалық іске асырылуы қарапайым болғандықтан, сызықты операторлар кеңінен қолданылады. Сигналдар координаталарын анықтау үшін

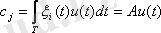(3. 5)

қатынасы қолданылады, мұндағы 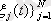- салмақтық функциялар жүйесі.

Қалпына келтіретін функция

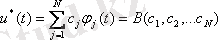(3. 6)

аппроксимациялаушы полиномымен беріледі, мұндағы 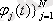базисті функциялар жүйесі.

Дискреттеу әдістері ең алдымен сигналдың координаталарын алу әдістеріне байланысты бөлінеді.

Егер салмақтық функциялар ретінде функциялары қолданылса сигналдың координаталары “өлшенген” болады. Ол кезде базистік функциялар ортогональды болады және 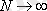болғанда u(t) - ға (3. 6) орта квадратты қатарына жинақталады.

Сондай-ақ қалпына келтірудің берілген қателігі кезінде координаталардың ең аз санын қамтамасыз ететін дискреттеу әдістері де маңызды. Оларды тиімді немесе шекті дискреттеу әдістері деп атайды.

u(t) сигналының белгілі 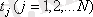уақыт кезеңдерінде алынған оның лездік мәндерімен ауыстырылатын дискреттеу әдістері кең таралған. Бұл жағдайда 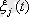салмақтық функцияларының ролін Дирактың дельта функциялары орындайды. (1. 11) сәйкес координаталары таңдауларын немесе

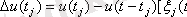
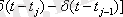көршілес таңдаулардың айырмасын береді деп айта аламыз. Дельта-функцияларды техникалық түрде іске асыру мүмкін емес болғандықтан әрбір таңдаудың ұзақтығы шекті. Санақтарды кілттік құрылғының басқарушы импульстің ұзақтығына байланысты белгілі бір уақыт аралығында алады. Импулсьтің ұзақтығы дискреттеу қадамынан аз болса, таңдаулар амплитудалары сигналдың лездік мәндеріне пропорционал болатын қысқа импульстер болып табылады.

3. 3 Таңдау көмегімен жасалатын дискреттеу әдістері

Дискреттеу әдістерін құру кезінде санақтарды таңдау критерийін тұжырымдау, оларды бастапқы сигнал бойынша қалпына келтіру процедурасын қою және қатені анықтау мүмкіндігін анықтау керек. Көрсетілген есептерді шығару дискреттелетін сигналдың белгілі бір математикалық моделін таңдаумен шешіледі.

Теориялық зерттеулерде әрбір іске асырылуы квазистационарлы кездейсоқ процесс болатын сигналдың моделі кең таралған. Бұл кезде дискреттеу қадамы спектрдің ең үлкен жиілігінен тәуелді болады. Санақтарды таңдаудың мұндай критерийі жиіліктік деп аталады.

Дискреттеу қадамын анықтаған кезде санақтардың коррелирленбеген дәрежесіне негізделуге болады. Мұндай критерий корреляциялық деп аталады.

Бірқалыпты дискреттеуді көбінесе n-ші дәрежелі аппроксимациялаушы көпмүшелерді қолданып іске асырады. Сигналдың математикалық моделі ретінде әрбір іске асырылуы (n+1) шектелген туындысы бар u(t) үздіксіз функциясы болып табылатын стационарлы кездейсоқ процесс алынады. Бұл кезде сигналдың динамикалық қасиеттері барлық түрлендіру аралығындағы оның n+1 туындысының ең үлкен модулімен беріледі. Санақтар ең үлкен ауытқу критерийі бойынша алынады.

Бірқалыпты дискреттеу кезінде қадам сигналдың динамикалық сипаттамаларының ең үлкен мәніне байланысты алынатындықтан, сигналдың лездік мәндері күрт өзгермейтін бөліктерде санақтардың артықтылығы пайда болады.

Санақтарда артықтылықты тиімді жоюды адаптивті бірқалыпты емес дискреттеу әдістері қамтамасыз етеді. Бұл жағдайда дискреттеу қадамдарының ұзақтығы сигналдың іске асырылу параметрлерінің мәндерімен тығыз байланысты. Санақтар таңдап алынған қалпына келтіру қателігі критерий ролін атқаратын белгілі бір мәнге жеткенде жасалады.

4 тарау. Ақпарат саны

Мәліметтер көзі әрбір уақыт кезеңінде кездейсоқ түрде мүмкін болатын шекті жағдайлар жиынтығының бірін қабылдайды делік. Мұндай көз дискретті мәліметтер көзі деп аталады. Әртүрлі жағдайлар оларды көзбен таңдау салдарынан іске асырылады. U көзінің әрбір жағдайына белгі түріндегі шартты белгілеу сәйкес келеді. N мүмкін болатын жағдайларға сәйкес келетін u ₁ , u ₂ , :, u _i , :, u _N жиынтықтары алфавит , ал N жағдайлар саны алфавит көлемі деп аталады. Мұндай көзбен мәліметтерді қалыптастыру оның кейбір u _i жағдайын таңдау және сәйкес белгіні беруге әкеліп соғады. Осылайша элементарлы дискретті мәліметтер ретінде көзбен берілетін u _i символын түсінеміз, бұл кезде Т уақыты кезеңінде көз дискретті мәліметтерді әрқайсысы t _i секунд ұзақтығы бар u _i символдарының жиынтығы болатын (мысалы, u ₅ , u ₁ , u ₃ ) элементарлы дискретті мәліметтер тізбегі ретінде бере алады. Мәлімет көзінің мұндай моделі іс жүзінде телеграфия және мәліметтерді беру жағдайларына сәйкес келеді (t _i =const) . Көздің кейбір жағдайлары жиірек, ал кейбіреулері сирек таңдалуы мүмкін. Сондықтан ол жалпы жағдайда U дискретті ансамблімен, демек олардың пайда болу ықтималдықтарының жиынтығымен сипатталады.

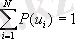, (4. 1)

мұндағы P(u _i ) - көзбен u _i жағдайын таңдау ықтималдығы. Мәліметтерді көзбен элементарлы дискретті мәліметтер жиынтығы ретінде бергенде толық ықтималдықты суреттеу ретінде u _i әртүрлі символдардың t ₁ , t ₂ , . . . , t _n кезеңінде бірге пайда болу ықтималдығы алынады, мұндағы n - тізбектің ұзындығы

. (4. 2)