Математика сабағында оқушылардың белсенділігін арттыруда пәнаралық байланыстын ықпалы

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 29 бет
Таңдаулыға:

Қазақстан Республикасының білім және ғылым министірлігі
Ілияс Жансүгіров атындағы Жетісу мемлекеттік университеті КЕАҚ

ДИПЛОМДЫҚ ЖОБА

Тақырыбы:
Математика сабақтарында пәнаралық байланыстарды жүзеге асыру

Мамандығы : 6В01502 Математика-информатика

Орындады: ________________ Сұлтанова А.А
(қолыподпись) (аты-жөні ФИО)
Жетекші: ________________ Тасболатова Р.Б
(қолыподпись) (аты-жөні ФИО)

Талдықорған 2021 жыл

МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 3
1. ОҚУ ҮРДІСІНДЕГІ ПӘНАРАЛЫҚ БАЙЛАНЫСТАРДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
1.1 Мектептегі білім беруде пәнаралық байланыстың алатын орны ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
1.2 Оқу процесінде пәнаралық байланыстарды іске асыру ерекшеліктері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..

2 . МЕКТЕПТІК МАТЕМАТИКА КУРСЫНДА ПӘНАРАЛЫҚ БАЙЛАНЫСТЫ ЖҮЗЕГЕ АСЫРУДЫҢ ӘДІСТЕМЕЛІК АСПЕКТІЛЕРІ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2.1 Математика сабағында оқушылардың белсенділігін арттыруда
пәнаралық байланыстын ықпалы ... ... ... ... ... ... ... ... ... ...
2.2 Математиканың басқа оқу пәндерімен байланысы ... ... ... ... ... ... .. ... ... ..
2.3 Мектеп математика курсындағы пәнаралық мазмұнды есептердің мәні және функциясы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

Кіріспе

Мектептің алдындағы басты мақсаттардың бірі - ғылым негіздерін оқытуда білім деңгейін көтеру. Осы мақсатқа жету оқу бағдарламасының мазмұнына, процесті ұйымдастыруда, оқытуда қолданылатын әдістер мен әдіснамалық тәсілдердің тиімділігіне қатысты. Сонымен бірге бұл тапсырманы орындау пәнаралық қатынастарда маңызды орын алады.
Бүгінгі таңда ғылымның барлық салалары бір-бірімен тығыз байланысты, сондықтан мектеп пәндері де бір-бірімен байланыста. Пәнаралық байланыс-бұл мектептегі ғылым негіздерін терең және жан-жақты зерттеудің тәсілі. Мектептегі математика курсында пәнаралық байланыстарды айқындау білімді одан әрі игеруге, ғылыми көзқарасты қалыптастыруға, қоғам құбылыстарының бір-бірімен қарым-қатынасына болуына ықпал етеді. Оның тәрбиелік мәні өте зор. Онымен қатар оқушылардың білім деңгейі артып, логикалық ойлауы дамиды. Пәнаралық қатынастарды жүзеге асыру материалды игеру кезінде қайталануды болдырмайды, уақытты үнемдейді, білім алушылардың ғылыми білімі мен дағдыларын қалыптастыруға жағдай жасайды.
Қазіргі уақытта мектеп пәндері бойынша көптеген оқу бағдарламалары мен оқулықтар бар. Бұл, әрине, мұғалімнің жұмысына еркіндік берді, оған сыныптың дайындығы мен оқушылардың мүдделерін ескере отырып, белгілі бір пән бойынша оқулықтардың оңтайлы жиынтығын таңдауға мүмкіндік береді.
Қазіргі ғылыми салаларда математикасыз жұмыс жасау қиын. Бұл білім алушыларға оқытылатын пәндердегі шындық құбылыстарының өзара байланысын көрсету үшін қажет.
Пәнаралық байланыстар- бұл:
- біріншіден, оқу құралы мен бағдарламалар арасындағы өзара келісім;
екіншіден, әр түрлі пәндер бойынша мұғалімдердің жұмыс жүйесіндегі үйлесімділік, сабақ барысында заттар мен құбылыстарды мұқият зерттеу;
- үшіншіден, оқушылардың басқа пәндер бойынша алған білімдерін қайта жаңғырту және оларды игеруге жататын жаңа материалға қолдану қабілетіне байланысты олардың ақыл-ой белсенділігі.
Көп салалы пәнаралық байланыстардың көмегімен оқушылардың білім алуы, дамуы және тәрбиелену міндеттерін сапалы және жаңа деңгейде шешу ғана емес, онымен бірге болмыстың күрделі мәселелерін тұтас көру және шешу үшін негіз қаланады. Сондықтан пәнаралық қатынастар оқушыларды оқыту мен тәрбиелеудің кешенді тәсілінің негізгі шарты және нәтижесі болып табылады.
Математика - бұл нақты өмірдегі кеңістіктік формалары мен сандық қатынастарды зерттейтін ғылым. Математика тек қана санау аппаратын, табиғат заңдылықтарын қарапайым алгебралық функциялар мен тригонометриялық функциялар түрінде сипаттаудың жолдарын ғана емес, сонымен қатар мектеп курсының пәндері бойынша мектептегі ғылыми білім деңгейін көтеруге көмектесетін қатынастар мен идеологиялық рөлдерді атқарады.
Ғылыми дүниетанымның қалыптастыру - барлық оқытылатын пәндерді қамтитын күрделі процесс. Атап айтқанда, жаратылыстану циклінің пәндері оқушыларға әлемнің бірлігі туралы түсінік алу үшін ерекше мәнге ие. Табиғат құбылыстарына тұтас ғылыми көзқарасты қалыптастыру осы пәндер арасындағы байланысты жүзеге асырудың арқасында мүмкін болады.
Табиғи математикалық цикл пәндерін оқытуда пәнаралық қатынастарды жүзеге асыру, атап айтқанда осы пәндердің мазмұнын жаңарту контекстінде өзекті мәселеге айналады. Бұл осы пәндердің арақатынасы оқу материалының мазмұнын және оны қабылдау тәртібін анықтауда шешуші белгі болып табылатындығына байланысты.
Қазіргі ғылымның математикалық процесі мектепте математиканы оқытуға айтарлықтай әсер етеді. Оқушыларға математиканы оқыту кезінде мұғалім ең алдымен математиканың пайда болуы нақты әлем екенін және біздің математика туралы біліміміз практикалық қолдану нәтижесінде осы нақты әлемге оралатынын дәлелдеуді мақсат етуі керек. Бұл білім неғұрлым терең және кең болса, өмірге ену дәрежесі соғұрлым жоғары болады.
Басқа тиісті пәндерді оқытуда математиканы оқытудың маңыздылығы және сабақта орындалған тапсырмалардың қолданбалы сипаты туралы көп айтылғанмен, тиісті пәндердің материалдары мен математика курсының есептерін қарастыратын болсақ, бұл мәселе әлі де ашық екенін атап өтуге болады.
Қазіргі уақытта математиканың пәнаралық қатынастарының маңыздылығын түсінудің ерекшелігі - оқушылар математиканы, математиканың техникадағы, жаратылыстану ғылымдарындағы, гуманитарлық ғылымдардағы, экономикадағы рөлін қоса алғанда әр түрлі дереккөздерден: газеттер, журналдар, теледидар және интернеттен алуы. Оқушылар математика сабақтарында алған білімдерін естіп-игергендерімен салыстырады және сабақта үйренген үстірт және дерексіз математика мен қазіргі ғылымның нақты проблемалары арасындағы байланысты көрмейді.
Өкінішке орай, мұғалімдердің көпшілігі негізінен оқулықтар мен оқулықтарға назар аударады және пәнаралық байланыстың қажеттілігін ескермейді.
Тақырыптың өзектілігі пәнаралық қатынастың педагогикалық маңыздылығымен, мектептегі математика курсын оқытуда пәнаралық қатынас орнату қажеттілігімен сипатталады.

Дипломдық жобаның мақсаты - пәнаралық байланыстарды негіздеу және дамыту және оларды математика сабақтарына енгізу болып табылады.

Дипломдық зерттеудің объектісі мектепте математиканы оқыту процесі болып табылады.

Дипломдық жобаның міндеттері:
1. Математиканы оқыту процесінде пәнаралық байланыстарды қолданудың теориялық негіздерін зерттеу.
2. Мектепте математиканы оқыту кезінде пәнаралық байланыстарды іске асырудың теориясы мен тәжірибесінің жай-күйін талдау.
3. Пәнаралық мазмұнды есептерді қолдана отырып, математика сабақтарын құру.

Дипломдық жобаның тәжірибелік мәні - жұмыста көрсетілген есептер және мектепте математиканы оқытуда пәнаралық мазмұнындағы есептерді қолдана отырып ұйымдастырылған сабақтардың мектептің оқу процесінде, жалпы білім беретін орта мектептерде математикадан оқу-әдістемелік құралдар құрастыруда, сонымен қатар педагогикалық мамандықта оқитын студенттердің математиканы оқыту әдістемесі пәнін оқу процесінде қолданыс таба алу.

3.2 Математиканың басқа оқу пәндерімен байланысы

Пәнаралық байланыс дегеніміз - пәндер мазмұнында табиғаттағы өзара байланыстардың реттеліп бейнеленуін қамтамасыз ететін дидактикалық шарт. Математикалық ерекшеліктердің арқасында пәнаралық қатынастардың жүзеге асырылуы өмір мен тәжірибенің, оқытудың байланысының талаптарының бірі болып саналады.
Қазіргі таңда ғылымның барлық делік салалары бір-бірімен өте тығыз байланыста, сондықтан мектептегі оқыту пәндері де бір-бірінен оқшауланбау керек. Мектептегі пәнаралық байланыстар ғылым негіздерінің тереңірек және де толық игерілуінің дидактикалық шарты әрі құралы болып саналады.
Оқыту пәндерін негізгі мен қосымша деп ажыратуға болмайды. Дегенмен әрбір мектепте оқушылардың қандай да болсын пәнге деген алуан түрлі пікірлері болады, кейбіреулері қызығушылық танытады, енді басқалары қызықпайды, кейбіреулері сыйластықпен қарайды, ендігі бірі жақтырмайды. Математика жайлы да бірмағыналы емес бағалау кездеседі: ықылассыздықтан қызығушылыққа дейін.
Математика пәні сияқты көлемді пәнаралық байланыс диапазоны бар оқыту пәндін атау қиын.
Мектеп математика курсындағы пәнаралық байланыстарды анықтау білімді терең игеруге, ғылыми көзқарасты, материалдық дүниенің бірлігін, табиғат пен қоғамдағы құбылыстардың өзара байланысын қалыптастырады. Мұның өте тәрбиелік мәні бар. Сонымен қатар, оқушылардың ғылыми білім деңгейін жоғарылатады, олардың шығармашылық және логикалық ойлау қабілеттерін дамытады. Пәнаралық байланыстарды жүзеге асыру материалды оқуда қайталауды қажет етпейді, уақытты үнемдейді және оқушылардың жалпы ғылыми білім мен біліктілігін қалыптастыруға қолайлы жағдай жасайды. Математика пәнін оқытудың мақсаттарының бірі, бұл оқушылардың бойында дүниетанымның қалыптасуы, оқушылардың нақты әлемді, өмірде болып жатқан өзара байланыс құбылысын түсінуге мүмкіндік беруде пәнаралық байланыс басты рөл атқарады. Математиканы оқыту процесінде балалардың білімі мен біліктерін, танымдық қабілеттерін дамыту үшін пәнаралық байланысты жүзеге асыру қажет.
Табиғаттың ұлы кітабы математикалық символдармен жазылған - деп Галилео Галилей айтқандай математика пәнін табиғаттан бөліп алып, жеке қарастыруға келмейді. Бұл - ғылымның әртүрлі салаларының арасында айқын шекара жоқ екендігі және олардың бір - бірімен тығыз байланыста болатыны туралы түсініктерді, сондай - ақ, дүниеге ғылыми көзқарасты қалыптастыруға табиғат құбылыстарының біртұтастығын, өзара байланысын көрсетуге мүмкіндік туғызады. Сонда баланың бір сабақта алған білімі, әсері, ойы, қиялы әрі қарай дами түсуі, әр пәннен басқа пәндерге көшудің үзіліссіздігін қамтамасыз етеді. Математика пәнін оқыту процесінде белгілі бір пәнаралық байланыс іске асырылады. Математика пәні - психология, педагогика, математика курсының теориялық негіздері пәндерімен тығыз байланысты. Сондай-ақ математикалық түсініктер мен ұғымдардың мән - мағынасын және мазмұнын жете түсінуге және тәжірибеде пайдалануға мүмкіндік туғызады.
Мектепте оқыту жоспары бойынша математика пәнін оқытуға бірінші сыныптан он бірінші-сынып аралығында 2000 дай оқыту сағаты бөлінеді. Онымен бірге, математиканы оқытуда қосымша факультативтік курстар да беріледі.
Мектептің оқу программасы мектептің негізгі алға қойған мақсаттарына сай болу қағидаттарына негізделген, оқушылардың 1-4 сынып (бастауыш), 5-9 сынып (9 жылдық мектеп), 10-11 сынып (орта мектеп) оқитын оқушылар үшін білімнің үздіксіздігін қамтамасыз етеді.
Оқушыларға орта(тоғыз жылдық) мектепті аяқтап кәсіби-техникалық оқу орындарында, арнайы орта білім беру мекемелерінде, кешкі мектептерде орта білімдерін жалғастыратын оқушылар орта білім берілетін мектепті аяқтайтын оқушылармен бірдей математикалық білім алулары керек. Орта білім алған барлық оқушылардың оқуын жалғастыруға тең мүмкіндіктері бар.
Жаратылыстану ғылымының барлық пәндерінің оқытылуы математикамен өте тығыз байланыста.
Пәнаралық байланыс мазмұны бар есептерге кейбір қойылатын талаптар:
1. тапсырманың құрамында математикалық әрі математикалық емес мазмұндағы мәселелер және де олардың арасындағы байланыстардың бейнеленуі керек;
2. тапсырмалар курстың программасына сәйкес болуы; есептегі қолданылатын материалдар оқыту үдерісіне керек компонент, курстың логикалық жалғасы болып кіруі қажет әрі оқудың мақсатына жетудің ролін атқаруы қажет;
3. тапсырма мазмұнына кіретін жағдайлар,түсініктер, терминдер, шығару тәсілдері оқушыларға түсінікті болуы қажет;
4. мектептің математика курсында қарастырылатын қолданбалы есептер әрқилы мақсаттармен, білім беру әрі дамыту, тиімді түрде қолданылуы ықтимал.
Математиканы оқыту бағдарламасында физика, география, тарих, химия, биология және басқа да оқу пәндермен байланысты кеңінен қолдану қажет. Математиканы оқыту кезінде ғылымдағы, сонымен қатар ғалымдардың өмірі мен іс-әрекеттеріндегі дәлелдерді қосқан орынды. Сонымен бірге биология, география, химия мұғалімдерімен интегралдық сабақтар өткізу мүмкіндігі бар.
Дәл осындай сабақтар оқушылардың мүмкіндіктерін кеңітеді, оларды қоршаған болмысты танып білуге, логикалық ойлауды дамытуға жетелейді.

2.2.4 Математиканың физикамен байланысы

Физика сабақтарында мұғалім математикалық тәсілдерді жиі қолданады:
- заңдарды жалпы және дәл формада өрнектеу үшін;
- кейбір теориялық алғышарттардың заңдылықтарын қорытындылау үшін;
- шығарып алынған формулалардың басқаға түрлендіру үшін;
- тікелей өлшеуге мүмкін болмайтын шамаларды табу үшін;
- әр түрлі есептеулер және есептерді шығару үшін.
Физиканы оқытудағы математикалық тіл заңдарды және тәжірибелі зерттеулердегі заңдарды қысқаша өрнектеудің, көптеген негізгі ережелердің теориялық түсіндірілуі үшін қолданылатын құрал.
Физикалық есептерді шығарғанда мұғалім математиканы жиі қолданады. Физика курсын оқытудың басында оқушылар математикалық символдарды және әріптік формулаларды қолдануға әдеттенеді. Математиканың белгілі бір курсын оқығаннан кейін оқушылар физикалық шамалардың арасындағы қатынастарды қысқа, ықшам жазу үшін, ал содан кейін есептеулерді жүргізу үшін қызмет атқаратынын түсінеді.
Жоғары сыныптарда физиканы оқытуда математиканың ролі ерекше жоғарылайды. Мұнда физикалық құбылыстарды экспериментальды оқытумен бірге физика мұғалімі физикалық зерттеуде мтематикалық анализді кең қолдануына болады, өйткені бұл оқушылардың математикалық дайындық деңгейі бойынша мүмкін. [15,104-107]
Мысалы, X сынып физика курсында Гармоникалық тербелістер тақырыбын оқуда оқушылар IX сынып алгебра курсынан үдеу мен координатаның, жылдамдық пен координатаның өзара байланысы біледі, яғни лездік жылдамдық уақыт бойынша координатаның туындысы, ал үдеу уақыт бойынша координатаның екінші туындысы болатыны туралы.
Осыдан мынадай қорытынды шығады: бұл теңдеуге сәйкес еркін тербеліс кезінде х координатасы уақытпен координатаның уақыт бойынша екінші туындысы координатаның өзіне тура пропорционал және оған таңбасы қарама-қарсы болатындай өзгереді.
Ары қарай мұғалім мына математикалық жағдайға сүйенеді: синус және косинус функциялары функцияның екінші туындысы қарама-қарсы таңбамен алынған сол функцияның өзіне тең деген қасиетке ие болады. Яғни, еркін тербеліс жасайтын дененің координатасы уақыт өткен сайын синус және косинус заңымен өзгереді. Осыдан гармоникалық тербелістер анықтамасы беріледі. Синус және косинус заңы бойынша жүретін уақыттан тәуелді физикалық шаманың периоды өзгерістері гармоникалық тербеліс деп аталады. Содан соң гармоникалық тербелістер косинус және синус көмегімен жазылады.

Математиканың географиямен байланысы

Атмосфера тақырыбын оқығанда география бағдарламасының математикамен байланысы өте тығыз болады. Осы тақырыпта температура, атмосфералық қысым, ылғалдылық, жауын-шашын, жел сияқты ұғымдар енгізілген.
VI сынып математика курсында бағанды және дөңгелек диаграммалар қарастырылады, арифметикалық ортаны есептейді, графиктерді оқиды. Осының барлығы орташа айлық және орташа жылдық мөлшердегі ауа температурасын алу үшін өте орынды, ал координаталық осьтегі екі нүктенің арасындағы қашықтықты есептеу - ауа температурасының амплитуласын табу үшін қолданылады. Оқушылар температураның жыл мезгіліне, биіктікке тәуелділік графигін қолданып, сұрақтарға жауап беруді үйренеді. Жел бағытының графигі бойынша желдің басым болатын бағытын анықтайды. Жауын-шашын мөлшері туралы көріністі көру үшін бағанды және дөңгелек диаграммалар сызады.
Математикада геометриямен танысқанда балалар фигураларды, бұрыштарды зерттейді. Геометрияның, геометриялық денелердің табиғаттағы маңыздылығы өте зор. Географиядан осыған нақты мысалдарды келтіруге болады. Интегралданған сабақта Пифагордың бірінші болып Жердің шар екені туралы ең қызықты жорамал жасағаны балалар үшін жаңалық болады. "Табиғатта бардың барлығы да мінсіз және үйлесімді болуы қажет. Бірақ ең жетілген геометриялық дене - ол шар. Демек, Жер - шар!" - деген Пифагор.
Сол сияқты стереометрия курсын оқығанда оқушылардың жер шары туралы білімдері қолданылады. Шар бетінің екі нүктесі арқылы жүргізілген үлкен дөңгелектің шеңберін қарастырғанда шар бетіндегі нүктелер арасындағы ең қысқа қашықтық сызығы әрқашанда үлкен шеңбердің доғасы бойымен жүргізілетінін атап өту қажет. Жер бетіндегі мұндай сызықтар ортодромдар деп аталады. Олар теңіз және әуе навигациясында үлкен практикалық мәнге ие: өйткені ең қысқа қашықтық бағытымен қозғалу әрқашанда тиімді.
Қазақстанның өзендері тақырыбындағы сабақтарда өзендердің су режим түрлерімен танысқанда бір мезгілде математикадағы Функция. Функцияның қасиеттері тақырыбы бекітіледі. Өйткені су режимінің түрі бір жыл ішіндегі судың жұмсалуын үлестіру бойынша анықталады, судың жұмсалуын үлестірудің графиктері функция графигі болып табылады. Осындай сабақтарда балалар функция, функцияның графигі өзімен өзі бар болатын астрактілі бірдеңе емес, тасқындардың болжамдарын құрастыру үшін қажетті буын, математикасыз ешбір су шаруашылығына қатысты шараларды, ол суландыру, сумен қамтамасыз ету, кептіру, су электростанциясының құрылысы, су қоймасының ғимараты болсын, өткізуге мүмкін емес екенін түсінеді.
Математикалық сабақтарда көрнекі құрал ретінде Қазақстан және дүниежүзілік географиялық карталар жиі қолданылады.
Мысалы, VI сыныпта Тік бұрышты координаталар жүйесі тақырыбын оқығанда Меркатор проекциясы бойынша орындалған градустық торы бар әлемдік географиялық карта ілінеді. Қысқаша түрде оқушыларға бұл картаны алғаш рет фламанд картографы Меркатордың 1569 жылы ұсынғаны туралы әңгімелеп айтылады. Сол уақыттан бастап кемемен теңізде жүруде кең таралды, өйткені теңізде жүрушілерге қашықтықтарды өлшеуді және бағыттарды салуды (тұрақты бағыт бойынша жүретін кеменің траекториясы) едәуір жеңілдетеді.
Жер бетіндегі нүктелердің географиялық координаттары - кеңдік және ұзақтық - оқушыларға география сабақтарынан таныс. Осыдан кейін жазықтықтағы нүктелердің координаттары туралы түсінік беріледі.
VI сыныпта Масштаб тақырыбын оқығанда интегралдық сабақ жүргізуге болады, мұнда сандық және сызықтық масштаб түсініктері қарастырылады. Оқушыларды географиялық картадағы санды масштабты сызықтыққа және керісінше аудару тәсілдерін үйретеді. Оқушыларға қатарынан географиядан есептер мен тапсырмалар беріледі.
Сандық масштабтың практикалық қолданылуы әр түрлі масштабты топографиялық карталарда кескінделген екі пункт арасындағы ара қашықтықты табу; картаның берілген масштабы және пункттердің шынайы ара қашықтығы бойынша картадағы осы пункттердің ара қашықтығын кескіндейтін кесіндінің ұзындығын табу; картадағы берілген пункттердің ара қашықтығы мен олардың арасындағы шынайы ара қашықтық бойынша картаның сандық масштабын табу мысалдарымен көрсетуге болады.
География мұғалімімен бірге математика жіне география сабақтарында қолданатын географиялық мазмұндағы көптеген қызықты тапсырмаларды құруға болады.
Мысал ретінде практикада қолданылатын бірнеше тапсырмаларды келтірейік.
1. Экватор (немесе меридиан) доғасының ұзындығын масштабы 1:50000000 болатын глобуста 15°, 30°, 45° анықтаңыз.
2. Алдыңғы масштабты глобуста 15°, 30°, 45° градустардағы кеңділігі 50°, 60°, 70° болатын параллельдік доғасының ұзындығын табыңыз.
3. Масштабы 1:10000 картада 13,4 см2 - ді құрайтын учаске ауданын жердегі м2, га және км2 анықтаңыз.
4. Егер учаске ауданы жерде 18 га құрайтын болса, онда масштабы 1:3000 болатын сызбада оны см2 анықтаңыз.
5. Егер 360 га тең жер картада 10 см2 аумақты алып тұрса, онда карта аумағының сызықтық масштабын табыңыз.
6. А-ға қатысты В пункті солтүстікке қарай 2 км қашықтықта және С пункті солтүстік-батысқа қарай 3 км қашықтықта А, В және С үш елді мекен орналасқан. D пунктіне қатысты Е пункті солтүстік-шығысқа қарай 2 км қашықтықта, ал F - шығысқа қарай 3 км қашықтықта орналасқан D, E, F - басқа үш елді мекен тағы бар. Сызбасын жасап, В және С пунктерінің ара қашықтығы Е және F пунктерінің ара қашықтығымен бірдей болатынын дәлелдеңдер.
7. Жаңбырдан кейін жаңбыр өлшеуіш ішіндегі суды мензуркаға құйғанда, 212 см - ге тең көлем алынды. Осы жерде жаңбыр нәтижесінде су қабатының қалыңдығы (0,1 см-ге дейін) қандай болды?
8. Алматыдын самолет ұшып шықты. Солтүстікке қарай 500 км ұшқасын, ол шығысқа қарай бұрылып, тағы 500 км ұшып, самолет оңтүстікке бұрылды да, тағы да 500 км ұшты. Содан кейін ол батысқа қарай бұрылды да 500 км ұшып, жерге қонды. Сұрақ, самолеттің қонған орны қай жерде орналасқан - Алматының өзінде немесе одан солтүстікке, оңтүстікке, батысқа не шығысқа қарай қандай қашықтықта?
Жұмыс процесінде оқушылардың пәнаралық байланыстар әсерінен танымдық қызығушылықтары жоғарылайды. Пәнаралық байланыстар білімге деген құштарлықты оятады, пәнге деген қызығушылықты бекітеді, білімді тереңдетеді, кәсіби жоспарда қызығушылықтың құрылуына мүмкіндік береді

2.2.2 Математиканың экономикамен байланысы

Экономикалық мазмұндағы, яғни шешуі математикалық аппараттың қолданылуын талап ететін экономика саласында қойылған есептерді қарастырайық. Қазіргі замандағы қоғам экономикаландырылған өмірде тұрады, ал мектеп математикасы (басқа да пәндер) бұл ерекшеліктерді еш елемейді деп А.С. Симонов айтқан сондықтан да математиканы оқыту саласындағы осы заманда көптеген зерттеушілер мектеп математика мазмұнына экономикалық мазмұндағы есептерді енгізу қажеттегін атап айтты.
Экономикалық мазмұндағы бірнеше есеп қарастырайық. Мұндай есептер, біздің ойымызша, оқушылардың білімдерін жаңғыртып, олардың оқуға деген себептерін жоғарылатып қана қоймай, сонымен бірге оқушыларда танымдық қызығушылықтарын оятады.
1-есеп. Салымшы шот ашып, оған қарапайым (капиталға айналдырусыз) мөлшерлеме бойынша жылдық пайызы 11,5 болатын 4 жылға 25000 теңге көлемінде ақша салды. Салымшы салымның жабуында алатын сома қандай болады? 4 жылдың ішінде салым қанша теңгеге өседі? Арттыру коэффициенті неге тең (яғни салым сомасы қанша пайызға өседі)?
Шешуі. Белгілеулер енгізейік. 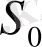- алғашқы капитал, p - пайыздық мөлшерлеме, n - толық жыл саны, 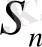- n-ші жылдың соңында пайыздармен есептелген капиталдың сомасы.
Онда қарапайым пайыздарды есептеу жолымен салымның қызмет ету моделі келесі түрде есептеледі:

Осы формула берілген экономикалық есептің математикалық моделін өрнектейді.
Есептің берілгендерін қолданып, есептеулер жүргізейік. n=4, p=11,5, ал болғандқтан
болатынын аламыз.
4 жылдан кейінгі салым сомасы 36500 теңге, яғни салым 11500 теңгеге өседі.
Қарапайым пайыздарды арттыру коэффициенті деп қатынасын айтады.
Бұл қатынас алғашқы салымының осы соманың банкте p% жылдық мөлшерлемемен қарапайы пайыздар сүлбесі бойынша n жыл сақталуы ішінде қанша есе өскенін көрсетеді. Берілген есепте арттыру коэффициенті 1,46 - ға тең.
2-есеп. Банктен 40 мың АҚШ доллары көлемінде 8 жылға төмендегі шарттар бойынша несие алынды: алғашқы үш жылға жылдық пайыздық мөлшерлеме 28%, келесі жылы ол 2%-ға артады, қалған жылдарға тағы да 2,5%ға артып отырады. Несие қайтару мерзімінің соңында күрделі пайыздардың жылдық есептелуінде банкке қайтарылуы қажет соманы табыңдар. (Күрделі пайыз (немесе басқаша айтсақ пайызға пайыз) - бұл бірінші кезеңде жиналған сома бастапқыға қосылғандағы капиталдың көбеюі, яғни, экономика тілімен айтсақ, бастапқы сома капиталға айналады да, жаңа кезеңде пайыз басқа, ұлғайтылған сомаға есептеледі.)
Шешуі. Барлық мерзімді жылдық пайыздық мөлшерлемеге тең кезеңдерге бөлейік. Бірінші кезеңде жылдық p1% есептеп қосылады, кезең ұзақтығы - n1 жыл, сосын n2 жыл жылдық p2% есептеп қосылады және ұзақтығы n3 жыл болатын үшінші кезеңде есептеу p3% болады және т.с.с. Онда бірінші кезеңде келесі сома есептеледі:

Екінші және үшіншіде сәйкесінше:
және
және т.с.с.
Сондықтан, n=n1 +n2 +...+n k жыл өткесін арттырылған S сома мынаған тең

Біздің есепте үш кезең бар. Бірінші кезеңде жылдық 28% есептеледі, кезең ұзындығы - 3 жыл, сосын 1 жыл 30% есептеп қосылады, және үшінші кезең - 4 жыл - 32,5% есептеп қосылады. Онда бірінші кезең бойынша келесі сома есептеледі:

Қайтару сомасы доллар дәлдікпен 336,122 мың АҚШ доллары.
3-есеп. Сұраныстың бағасы мен өлшемінің қатынасы кестеде берілген. Икемділік коэффициентін анықтау қажет. Сатушының іс-әрекетін бағалау.
2.2.2.1 кестесі

НҰСҚАЛАР
ӨНІМ БІРЛІГІНІҢ БАҒАСЫ
P
САТУ КӨЛЕМІ QD
ТҮСІМ
P·QD
Бастапқы жағдайлар
50 теңге
20
1000 теңге
Өзгертілген жағдайлар
60 теңге
15
900 теңге

Шешуі:
;
Қорытынды: Сұраныс икемді. Сатушының іс-әрекеті дұрыс емес, өйткені сұраныстың икемділік шарттарында бағаны көтеру емес төмендету пайдалы.
2.2.2.2 кестесі

НҰСҚАЛАР
ӨНІМ БІРЛІГІНІҢ БАҒАСЫ
P
САТУ КӨЛЕМІ QD
ТҮСІМ
P·QD
Бастапқы жағдайлар
40 теңге
20 кг
800 теңге
Өзгертілген жағдайлар
45 теңге
18 кг
810 теңге

Шешуі:
,
Қорытынды: Сұраныс икемді емес. Сатушының әрекеті дұрыс, өйткені сұраныстың икемді емес жағдайында бағаны аздап көтеру пайдалы. Действие продавца верное, т.к. в условиях неэластичного спроса выгоднее осуществлять незначительное повышение цены.
Осы есептердің шығарылуынан жасалған қорытындыны кесте түрінде көрсетейік.
Егер баға мен түсім қарама-қарсы бағытта өзгерсе, онда біз икемді сұраныс тауарын аламыз. Егер түсім мен баға бір бағытта өзгерсе, онда икемді емес сұраныс тауары болғаны.
2.2.2.3 кестесі

ИКЕМДІЛІК ТИПІ
БАҒАНЫҢ ӨЗГЕРУІ
ТҮСІМНІҢ ӨЗГЕРУІ
баға мен түсімнің өзара өзгеруі
Сұраныс икемді
Өсу
Төмендету
Төмендету
Өсу
Қарама - қарсы
Сұраныс икемді емес
Өсу
Төмендету
Өсу
Төмендету
Бірдей
Сұраныстың икемділік бірлігі
Өсу
Төмендету
Өзгеріссіз
Бағаның өзгеруіның түсімге әсері жоқ

4-есеп. Тауар бағасы мен сұраныс өлшемінің қатынасы Q= 38-3p функциясымен берілген. 5 теңге және 7 теңге бағадағы икемділік коэффициентін анықтаңдар.
Шешуі:
Qd=38-3p
p1=5т.
=7т.

Қорытынды: Тауардың бағасы 5 теңге болғанда сұраныс икемді емес. 7 теңге болғанда сұраныс икемді болады.
5-есеп. Тауар бағасы мен сұраныстың өлшемінің қатынасы Qd=21-5P функциясымен берілген. Қандай бағада тауарға сұраныс икемді емес (Ер = 0,9) немесе икемді (Ер = 1,1) болады.
Шешуі:

1) 2)
p2-? 5P=0,9 (21-5P) 5P= 1,1(21-5P)
p1-?
5P=18,9-4,5P 5P= 23,1 - 5,5P
9,5P=18,9 10,5P=23,1
P1=1,99 P2=2,2
Қорытынды. Тауардың құны P=2,2 теңге болғанда сұраныс икемді болады, құны P=1,99 болса сұраныс икемді емес. [14,10]
Оқушылардың назарына математикалық модельді құруда қарапайым және күрделі пайыздар аппаратын қолданатын қолданбалы есептер мысалы ретінде қаражат сипатындағы есептерді ұсынуға болады.
Экономика мазмұнындағы есептер практикалық есептер болып табылады. Ал оларды шығару орта мектеп математика мазмұнын сапалы игеруге мүмкіндік береді, алған білімдері мен іскерліктерін экономикаға аудару мүмкіндігін береді. Ал бұл оқушылардың қолданбалы сипаттағы есептерге және жалпы математикаға деген қызығушылықтарын белсендіреді. Мұндай есептер оқытудың қолданбалылық бағыттылығын толығымен жүзеге асыруға және оқу материалының өзін сапалы түрде игеруге және осыған ұқсас есептерді шығару іскерлігін қалыптастыруға мүмкіндік туғызады.

3.0.3 Математиканың сызумен байланысы

Осы екі пән мектеп курсында материалдық өмірдегі кеңістік формаларын және кеңістік қатынастарды зерттеумен айналысады.
Математика бағдарламасының түсініктеме хатында геометрияны оқытудың мақсаты жазықтықтағы фигуралардың қасиеттерімен таныстыру, кеңістіктегі елестетуді дамыту болып табылады. Мұнымен қатар практикалық дағды мен іскерлік қалыптасуы керек, бұған өлшеулерді орындау, практикалық сипаттағы әртүрлі есептерді шығару іскерліктері де кіреді. Осы есептер сызу сабақтарында да шығарылады; осы пәндерді оқытудағы байланыстардың қажеттілігі геометрияда да, сызуда да оқушылардың сызбалар орындауымен түсіндіріледі. Сонымен қатар геометрия сызу пәні үшін теориялық негіздер береді, ал сызу пәнін оқу процесінде қалыптасатын салу дағдылары геометрия пәнінде қолданылады. Сызу мұғаліміне оқу материалын түсіндіру барысында оқушылардың геометрия курсынан алған теориялық мәліметтеріне жиі сүйену қажет болады. Сол сияқты геометрия мұғалімдері салумен байланысты сұрақтарға үлкен назар аударуралы қажет.
Кейбір геометриялық есептерді графиктік түрде шығарғанда циркуль және сызғышпен ғана шектелмеу керек, өйткені бағдарлама салу есептерін шығаруды үйретуде көп құралдардың қолануын талап етеді. Геометрия сабақтарында сызу құралдарының рационалды қолданылуы, бір жағынан, сызуға арналған есептерді тиімді шығаруға мүмкіндік берсе, екінші жағынан, сызу сабақтарындағы сызбаларды орындауда қолданылатын белгілі дағдылардың жасалуына мүмкіндік береді. Осы міндеттің орындалуы үшін геометрия сабақтарында перпендикуляр түзулерді салуда тек бір сызба бұрыштығын ғана емес, бұрыштық пен сызғышты немесе екі бұрыштықты қолданылу қажет.
Геометрия сабақтарында параллелограммды, ромбты, трапецияны, шеңберге жанаманы және т.б. сызуға байланысты басқа да есептер қарастырылады. Барлық аталған есептер рациональды яғни сызу сабақтарында және конструкторлық бюро жұмыстарының практикасында қолданылатын тәсілдермен шығарылуы өте маңызды. Осы есептерді бұрыштық және сызғыш көмегімен шығаруда мұғалім қандай да бір есепті терең талдау, дәлелдеу және зерттеуге қажетті уақытты үнемдейді.
Сызудағы кейбір шартты кескіндеулер геометрия сабақтарында рационалды қолданылуын табылуы орынды.
Мұнда сызба сызықтарымен, шрифтпен және өлшемдерді белгілеумен байланысты мемлекеттік стандарттың қолданылуы туралы айтылды. Бұл геометриялық сызбалардың сапасын жақсартуға, түсінікті және жетілуіне мүмкіндік береді. Салуға арналған есептерді шығарғанда оқушыларға сызу сабақтарында да, математика сабақтарында да бірдей талап қою керек.
Сызу сабақтарында оқушылар теориялық білімді бекітеді, есептеу дағдыларын шынықтырады, құрастыру дағдыларына иемденеді.

2.2.5 Математиканың экологиямен байланысы

Математика табиғи объектілер мен құбылыстардың күйіне, адамның табиғи және әлеуметтік ортадағы оң және теріс нәтижелеріне сандық баға беру ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.