Қарапайым тригонометриялық теңдеулерді шешуді оқыту

Қазақстан Республикасының Білім және ғылым министрлігі

Қарағанды “Bolashaq” жоғарғы колледжі

«Математиканы оқыту теориясы мен әдістемесі» пәні бойынша

КУРСТЫҚ ЖҰМЫС

Тақырыбы: «Тригонометриялық теңдеулер мен теңсіздіктерді шешуге үйрету әдістемесі»

Мамандық: 0111000 - «Негізгі орта білім беру»

Біліктілігі: 0111063 «Математика мұғалімі»

Орындаған: МТ-17-1 тобының студенті

Болатбек А.

Жетекшісі: Жақыпбай Г. Е.

Қарағанды 2021

Мазмұны

Қорытынды . . . 33-34

Пайдаланған әдебиеттер тізімі . . . 35

Қосымшалар . . . 36-

КІРІСПЕ

Қазақстан Республикасы білім және ғылым министрлігінің нұсқалығына сәйкес, егер біз Қазақстан экономикасын, мәдениетін дамытып, жоғары дамыған елдердің қатарына жеткіземіз десек, онда бірінші орында білімді дамытуға тиіспіз. Ол үшін Қазақстанды болашақта өрге жетелейтін білікті мамандар даярлап, Отанына адал қызмет ететін азамат тәрбиелеп шығаруымыз керек. Қазіргі кезде осы мақсаттарды жүзеге асыру үшін жалпы білім беретін орындарға қойылған талаптар қатаңдалып, күннен күнге өсуде. Соның ішінде мектеп курсындағы гуманитарлық пәндер арасында математиканы оқыту үлкен іскерлікті қажет етеді. Мектепте математиканы оқыту - онымен тығыз байланыста жүретін пәндерді меңгеруге, күнделікті тұрмысқа қажетті біліктілік пен дағдыны қалыптастыруға және математиканы тереңдетіп оқытуға тиіс. Математиканы тереңдетіп оқыту - оқушының математикаға тұрақты қызығушылығын тудырып, олардың математикалық қабілеттілігін дер кезінде анықтап, дамуына ықпал етеді де жоғарғы оқу орнына түсуге дайындық мәселелерін шешеді. Оқушылардың математикалық даму дәрежесі олардың есеп шығару қабілеттілігінен көрінеді. Кез - келген қиын есепті шығару оқушылардың үлкен еңбекті талап етеді. Мұғалімнің міндеті баланың бойындағы қасиеттерді ояту болып табылады.

Ол үшін мұғалімнің үздіксіз ізденуін, әдістемелік - теориялық білімін жүйелі арттырып отыруын, терең ойлануын, оқушылардың психологиясын зерттеп, тақырып ерекшелігін жете талдай білуін қажет етеді. Әсіресе бұл талаптар жоғары сыныптарда күшейе түседі. Соның ішінде 10 - сыныпта оқытылатын тригонометрия тақырыбының өзі үлкен бір тарау болып келеді. . Олар:

1. Тригонометриялық функциялар, олардың қасиеттері және графиктері

2. Кері тригонометриялық функциялар

3. Тригонометриялық теңдеулер және теңсіздіктер

Соның ішінде біз тригонометриялық теңдеулер, теңсіздіктер және олардың жүйелерін шешу әдістерін қарастырамыз. Бұлардың ішіндегі тригонометриялық теңдеулер, теңсіздіктер тақырыбы өте күрделі. Сондай-ақ, тригонометриялық теңсіздіктерді шешу оқушылардың тригонометрия бойынша барлық оқу материалдарымен байланысты білімдерін жүйелеудің алғышарттарын жасайды (мысалы, тригонометриялық функциялардың қасиеттері, тригонометриялық өрнектерді түрлендіру әдістері және т. б. ) және алгебрада зерттелген материалмен тиімді байланыс орнатуға мүмкіндік береді (теңдеулер, теңдеулердің эквиваленттілігі, теңсіздіктер, алгебралық өрнектерді бірдей түрлендіру және т. б. ) . Оқушылар тригонометриялық теңдеулер мен теңсіздіктерді шешкенде үлкен қиындықтарға кездеседі. Сол себепті де мен өзімнің курстық жұмысымның тақырыбын «Тригонометриялық теңдеулер мен теңсіздіктерді шешуге үйрету әдістемесі» деген тақырыпқа арнадым.

Зерттеу объектісі - математиканы оқыту процессі.

Зерттеу пәні - тригонометриялық теңдеулер мен теңсіздіктерді шешу бағытталған әдістеме.

Зерттеу гипотезасы: егер тригонометриялық теңдеулер мен теңсіздіктерді бөліп алсақ және әдістемесін құрсақ, онда бұл сапалы түрде тригономериялық теңсіздіктерді шешуге ықпал етеді. Тригонометрияны сапалы зерттеумен, біз оқыту процесін түсінеміз, сонымен қатар тұлғалық бағдарлы оқытуды жүзеге асырылатынын ескере отырып, формальді білім беру және схоластикалық пысықтауды іске асыру кезінде оған жол берілмейді, яғни тригонометрияны зерттеу логикалық, оқу - танымдық ойлауға сүйенуге тиіс, бұл ретте оқушыларға саралау және даралау мүмкіндіктері беріледі.

Гипотезаның зерттеу процесінде және зерттеудің дұрыстығын тексеру үшін, келесі міндеттерді шешу қажет болды:

−Әдістемелік әдебиеттерді зерттеп, психологиялық - педагогикалық талдау
жүргізу;
-Математиканы оқытудағы тригонометриялық теңдеу мен теңсіздіктередің рөлін анықтау;

-Тригонометриялық теңдеулердің негізігі шешу амалдарын бөлу;
-Тригонометриялық теңсіздіктерді шешу әдістерін жіктеу;
-Тригонометриялық теңсіздіктерді шешу әдістерінде білік пен дағдыны
қалыптастыру;
-Құрылған әдістеме бойынша эксперимент жүргізу.
Берілген есептерді шешу үшін келесі әдістер қолданылды:
Психологиялық - педагогикалық және әдістемелік әдебиеттерді талдау;
оқулықтарды, оқу - әдістемелік құралдарды, дидактикалық материалдарды
талдау; бақылау, мұғалімдермен әңгімелесу, педагогикалық эксперимент.
Жұмыс құрылымы: Жұмыс екі тараудан тұрады.

Кіріспесінде зерттеудің өзектілігі атап өтілді. Бірінші тарау математика
курсындағы тригонометрияның теориялық материалдарына арналды, қарапайым тригонометриялық теңсіздіктердің шешу амалдары, әдістемесіне арналды, ал екінші бөлімінде тригонометриялық теңдеулер мен теңсіздіктерің шешу әдістемелеріне толығымен тоқталуға арналады.

Зерттеудің мақсаты - жалпы тригонометриялық теңдеулердің, теңсіздіктердің түрлерін және олардың шешу әдістерін талдау.

Зерттеу міндеті:

1. Тригонометриялық теңдеулердің, теңсіздіктердің шешу жолдарын көрсету. 2. Тригонометриялық теңдеулерді және теңсіздіктерді шешкенде ыңғайлы әрі оңай жолын таңдауға үйрету.

1. Мектеп курсындағы тригонометриялық теңдеулер мен теңсіздіктерді оқыту әдістемесінің теориялық негіздері

1. 1 Тригонометриялық функциялардың графиктері мен қасиеттері

Ең бірінші әрбір тригонометриялық функциялардың графигін салуға тоқталайық.

1 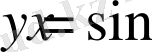функциясын қарастырамыз

Функцияның:

1) анықталу облысы $-$ барлық нақты сандар жиыны, яғни

2) мәндер жиыны 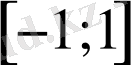кесіндісі, яғни

3) , функция периодты, оның ең кіші оң периоды 2п .

4) функция тақ, өйткені .

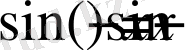5) 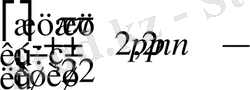кесінділерінде функция бірсарынды өспелі, кесінділерінде бірсарынды кемімелі.

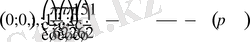нүктелерінің координаталық жазықтыққа түсіріп 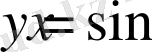функциясының 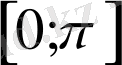кесіндісінің графигін саламыз (4-сурет) .

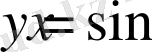функциясы тақ функция болғандықтан, оның графигі бас нүктеге қарағанда симметриялы қисық. Осы қасиетті пайдаланып, 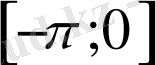аралығында графикті жалғастырамыз. Сонда, 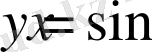функциясының 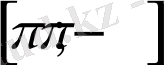кесіндісіндегі графигін аламыз

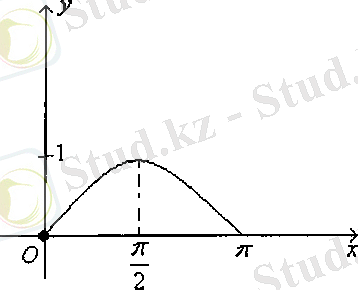
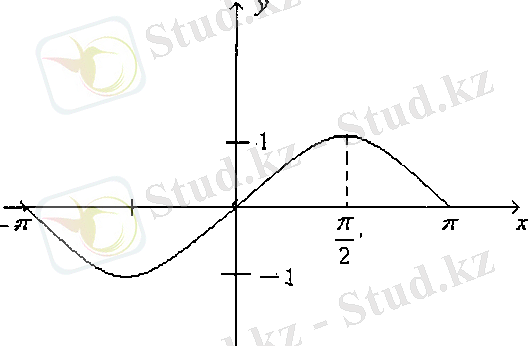
Сурет-1 Сурет-2

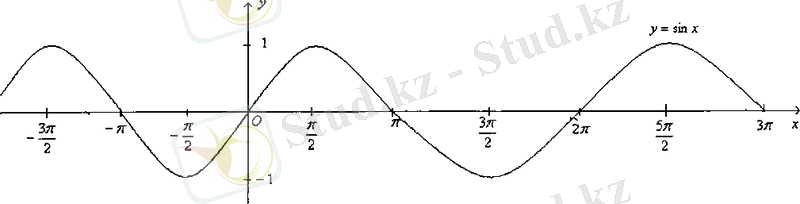
Демек, 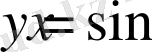функциясының толық бір период ішіндегі графигін салдық. Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы функция графигін салуға болады.

Сурет-3

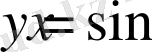функциясының графигін синусоида қисығы деп атайды.

2 Функциясын қарастырамыз.

Функцияның:

1) анықталу облысы -барлықнақты сандар жиыны, яғни $x \in R$ .

2) мәндер жиыны 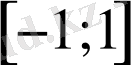кесіндісі, яғни

3) , функция периодты, ең кіші оң периоды 2π .

4) функция жұп, өйткені

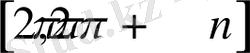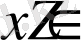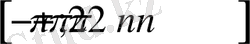
5) , кесінділерінде бірсарынды кемімелі және 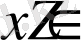кесінділерінде бірсарынды өспелі функция.

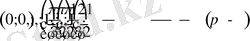нүктелерін координаталық жазықтықта белгілеп, $y = cosx$ функциясының кесіндідегі графигін саламыз (7-сурет) .

функциясы жүп функция болгандықтан, оның графигі ордината осіне қарағанда симметриялы қисық. Осы қасиетті пайдаланып, аралығында графикті жалғастырамыз. Сонда, функциясының кесіндісіндегі графигін аламыз.

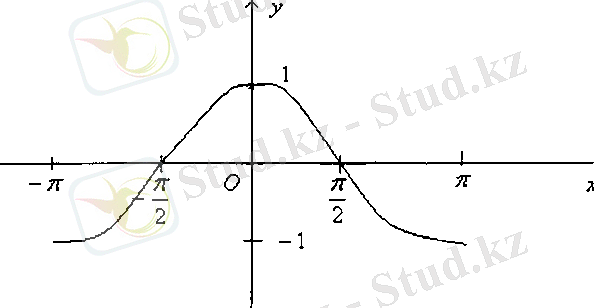
Сурет-4 Сурет-5

Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы функцияның графигін салуға болады (8-сурет) .

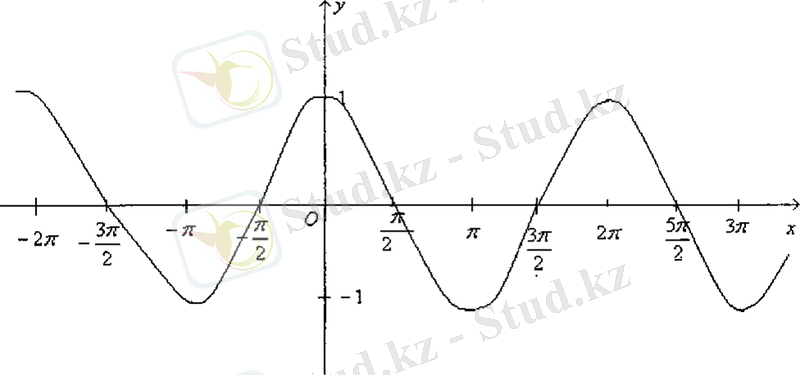
Сурет-6

функциясының графигін косинусоида қисығы деп атайды.

Сонымен қатар 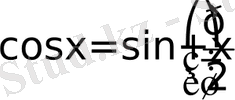екенін ескеріп функциясының графигін функциясының графигінен Ох осінің бойымен қашықтығына теріс бағытта параллель көшіру арқылы да алуға болады.

Функциясын қарастырайық.

Функцияның:

1. Анықталу облысыжиынынан басқа барлық нақты сандар
2. Мәндер жиыны - барлық нақты сандар жиыны, яғни
3. функция периодты π саны;
4. функция тақ, өйткені
5. , интервалдарында функция бірсарынды өспелі.

Енді $у\ = tgх$ функциясының графигін салайық.

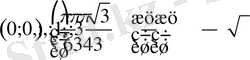нүктелерін координаталық жазықтыққа белгілеп, аралығында функциясының графигін саламыз.

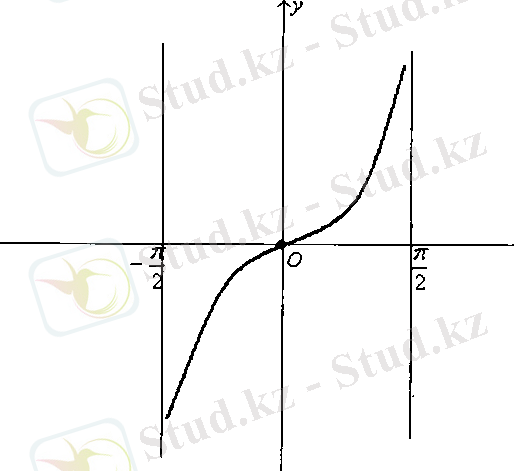
Сурет-7 Сурет-8

Функциясы тақ функция болғандықтан, оның графигі бас нүктеге қарағанда симметриялы қисық екенін ескеріп, жалғастырамыз. Сонда $у\ = tgх$ функциясының 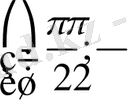интервалында графигі шығады (11-сурет) .

Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы функцияның графигін салуға болады (12-сурет) .

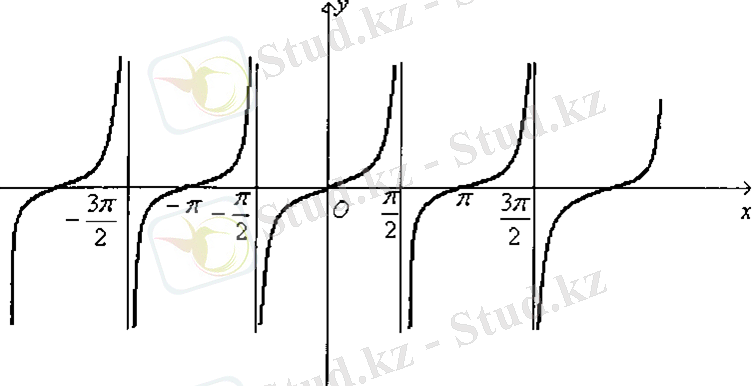
Сурет-9

функциясының графигін тангенсоида қисығы деп атайды.

Функциясын қарастырайық

Функцияның:

1. анықталу облысы:жиынынан басқа барлық нақты сандар жиыны себебі,
2. мәндер жиыны - барлық нақты сандар жиыны, яғни
3. тақ функция. Негізгі периоды π.
4. функция тақ, өйткені
5. интервалында бірсарынды өспелі. функциясы тақ функция болғандықтан, оның графигі у нүктеге қарағанда симметриялы қисық.

Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы Функцияның графигін салуға болады (13-сурет) .

Сурет-10

$у\ = \ ctgх$ функциясының графигін котангенсоида қисығы деп атайды

1. 2 Қарапайым тригонометриялық теңдеулерді шешуді оқыту

Анықтама . Белгісіз (айнымалысы) тригонометриялық функцияның аргументі түрінде берілген ттеңдеуді тригонометриялық теңдеу деп атайды.

Тригонометриялық теңдеулерді шешуді негізінен мынадай қарапайым тригонометриялық теңдеулерге келтіріп алып шешеді: .

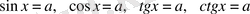Енді осы теңдеулерді шешу тәсілдерін қарастырайық.

$\cos{x =}a$ тригонометриялық теңдеуі

$\cos{x =}a$ теңдеуін қарастырайық.

Егер $a > 1$ болса, онда $\cos{x =}a$ тедеуінің шешімі болмайды. Себебі ${у = \cos}x$ функциясының мәндер жиыны $\lbrack - 1; 1\rbrack$ кесіндісі.

Егер $a$ $\mathbf{m}$ 1 болса, онда $\cos{x =}a$ теңдеуінің шешімі болады. Арккосинустың анықтамасы бойынша берілген теңдеудің $\lbrack 0; \pi\rbrack$ кесіндісінде бір ғана шешімі бар және ол шешім arccos $a$ (19. 1. 1-сурет) .

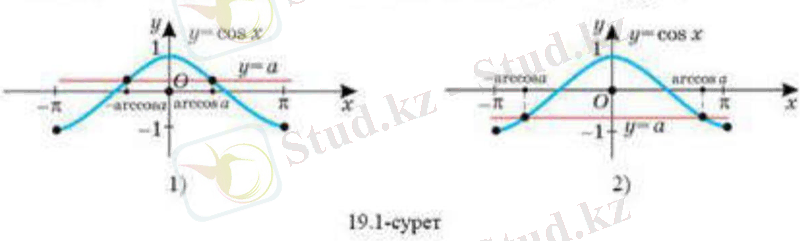
косинус функциясы жұп функция болғандықтан, $\lbrack - \pi:0\rbrack$ кесіндісінде $\cos{x =}a$ теңдеуінің -arccos $a$ - ға тең бір ғана шешімі бар (19. 1. 2-сурет) .

Демек, $\lbrack - \pi; \pi\rbrack$ кесіндісінде $\cos{x =}a$ теңдеуінің екі шешімі бар: arcos $a$ мен - arcos $a$ және ол шешімдер $a$ =1 болғанда бірдей.

${у = \cos}x$ функциясы периодты болғандықтан, теңдеудің қалған шешімдері табылған шешімдерден 2π n -ге( n- бүтін сан) ерекшеленеді (19. 2-сурет) .

$\cos{x =}a$ тедеуінің түбірлерін табудың жалпы формуласы:

$x = \pm \arccos{a + 2\pi n}$ , мұндағы n- бүтін сан және $a$ $\mathbf{m}$ 1.

$a$ =1 болғанда, $\arccos{a\ мен - \arccos a}$ сандары бірдей. Сондықтан cos x=1 теңдеуінің шешімін табу үшін х=2π n ( n- бүтін сан немесе n∈ℤ ) формуласы қолданылады.

$\cos{x =} - 1$ теңдеуінің шешімдер жиынын $\left\{ \pi + \ \right. \ 2\pi n\left. \, \ n \in \mathbb{Z} \right\}$ түрінде жазады. cos x=0 теңдеуінің шешімдер джиыны: $\left\{ \frac{\pi}{2} + \ \pi n, \ \left. \ n \in \mathbb{Z} \right\} \right. \$ .

1-мысал. cos x= $\ \frac{\sqrt{2}}{2}$ теңдеуінің шeшімін табайық.

Шешуі: Мұнда $a$ = $\ \frac{\sqrt{2}}{2}$ , яғни $a$ $\mathbf{m}$ 1 болғандықтан, 13-кесте бойынша х= $\pm$ arccos $\frac{\sqrt{2}}{2} + 2\pi n, \$ n∈ℤ. Енді arccos $\ \frac{\sqrt{2}}{2} = \frac{\pi}{4}$ болатынын ескеріп, х=± $\frac{\pi}{4} + 2\pi n, \$ n∈ℤ аламыз .

Жауабы: х=± $\frac{\pi}{4} + 2\pi n, \$ n∈ℤ.

2-мысал. cos $\left( 2х - \frac{\pi}{5} \right)$ = $- \frac{\sqrt{3}}{2}$ теңдеуінің шeшімін табайық.

Шешуі: Мұнда $a$ = $- \ \frac{\sqrt{3}}{2}$ , яғни $a$ $\mathbf{m}$ 1 болғандықтан, 13-кесте бойынша 2х- $\frac{\pi}{5}$ = $\pm$ arccos $\left( - \frac{\sqrt{3}}{2} \right) + 2\pi n, \$ n∈ℤ. Енді arccos $- \frac{\sqrt{3}}{2} = \pi - \arccos{\frac{\sqrt{3}}{2} = \pi - \frac{\pi}{6} = \frac{5\pi}{6}}$ екенін ескерсек, 2х- $\ \frac{\pi}{5} =$ $\pm \frac{5\pi}{6} + 2\pi n, \$ n∈ℤ аламыз . Cоңғы теңдеуде - $\ \frac{\pi}{5}$ қосылғышын теңдеудің екінші жағына шығарып, екі бөллігін да 2 санына бөлеміз, сонда 2х $=$ $\pm \frac{5\pi}{6} + \frac{\pi}{5} + 2\pi n, \$ n∈ℤ, х $=$ $\pm \frac{5\pi}{12} + \frac{\pi}{10} + \pi n, \$ n∈ℤ.

Жауабы: х $=$ $\pm \frac{5\pi}{12} + \frac{\pi}{10} + \pi n, \$ n∈ℤ.

${sin}{\delta =}a$ тригонометриялық теңдеуі

Егер $a > 1$ болса, онда $\sin{x =}a$ тедеуінің шешімі болмайды. Себебі ${у = \sin}x$ функциясының мәндер жиыны $\lbrack - 1; 1\rbrack$ кесіндісі.

Егер $a$ $\mathbf{m}$ 1 болса, онда $\sin{x =}a$ теңдеуінің шешімі болады. Арксинустың анықтамасы бойынша $\left\lbrack - \frac{\pi}{2}; \frac{\pi}{2} \right\rbrack$ кесіндісінде берілген теңдеудің бір ғана шешімі бар және ол шешім arcsin $a$ -ға тең (19. 3. 1-сурет) .

$\left( \frac{\pi}{2}; \frac{3\pi}{2} \right)$ аралығында у=sinx функциясы кемиді және -1-ден 1-ге дейінгі, 1-ді қоса алғандағы, мәндерді қабылдайды. Сондықтан түбір туралы теорема бойынша осы аралықта ${у = \sin}x$ теңдеуінің бір ғана түбірі бар және ол түбір π-arcsin a-ға тең (19. 3. 2-сурет) .

${у = \sin}x$ функциясының периодтылығын (периоды 2π-ге тең) ескерсек, теңдеудің барлық шешімдерін жазудың формулаларын аламыз:

x = arcsin $a$ + 2π $n$ , x = π - arcsin $a$ + 2π $n$ ( $n -$ бүтін сан) (19. 4-сурет) .

Осы екі формуланы біріктірсек,

$x = \ ( - 1) ^{k}\arcsin{a + \ }\pi k$ ( $k - бүтін\ сан\ немесе\ k$ ∈ℤ)

формуласы шығады.

$\sin{x = 1}$ теңдеуінің шешімдер жиынының жазылу түрі:

$\left\{ \frac{\pi}{2} + \ 2\pi n, n\mathbb{\in Z}\ \right\}$ .

$\sin{x = - 1}$ теңдеуінің шешімдер жиынының жазылу түрі:

$\left\{ - \frac{\pi}{2} + \ 2\pi n, n\mathbb{\in Z}\ \right\}$ .

$\sin{x = 0}\$ теңдеуінің шешімдер жиынының жазылу түрі:

$\left\{ \pi n, n\mathbb{\in Z}\ \right\}$ .

3-мысал. sin x= $\ \frac{1}{2}$ теңдеуінің шeшімін табайық.

Шешуі: Мұнда $a$ = $\ \frac{1}{2}$ , яғни $a$ $\mathbf{m}$ 1 болғандықтан, 14-кесте бойынша х= $( - 1) ^{k}$ arcsin $\frac{1}{2} + \pi k, \$ k∈ℤ. Енді arcsin $\ \frac{1}{2} = \frac{\pi}{6}$ болатынын ескеріп, х= $( - 1) ^{k}\frac{\pi}{6}$ $\frac{\pi}{4} + \pi k, \$ k∈ℤ аламыз .

Жауабы: х= $( - 1) ^{k}\frac{\pi}{6}$ $\frac{\pi}{4} + \pi k, \$ k∈ℤ.

${{tg}x} = a$ тригонометриялық теңдеуі

${{tg}x} = a$ теңдігі орындалатындай $a$ -ның кез келген мәнінде $\left( - \frac{\pi}{2}; \frac{\pi}{2} \right)$ интервалына тиісті бір ғана х саны бар, ол сан arctg a . Сондықтан ${{tg}x} = a$ теңдеуінің $\left( - \frac{\pi}{2}; \frac{\pi}{2} \right)$ интервалына бір ғана түбірі бар. Бұл интервалдың ұзындығы π-ге тең. у= ${tg}x$ функциясының периоды да осы санға тең. Сондықтан ${tg}x$ = $\ a$ теңдеуінің қалған түбірлері табылған түбірден π n -ге( n- бүтін сан) айырмашылығы бар.

Демек, ${{tg}x} = a$ теңдеуінің шешімі x = arctg $a$ + π $n$ , мұндағы $\ n -$ бүтін сан, формуласы бойынша табылады, шешімдер жиыны $\left\{ arctg\ a\ + \ \pi n, n\mathbb{\in Z}\ \ \right\}$ түрінде жазылады.

4-мысал. ${{tg}x} = - \sqrt{3}$ теңдеуін шешейік.

Шешуі: х = $\ arctg\ ( - \sqrt{3}) \ + \ \pi n, n\mathbb{\in Z}$ немесе х = - $\frac{\pi}{3}$ + $\ \pi n, n\mathbb{\in Z}$ .

Жауабы: х = - $\frac{\pi}{3}$ + $\ \pi n, n\mathbb{\in Z}$ .

${{сtg}x} = a$ тригонометриялық теңдеуі

$с{{tg}x} = a$ теңдігі орындалатындай $a$ -ның кез келген мәнінде $(0; \pi)$ интервалына тиісті бір ғана х саны бар, ол сан arсctg a . Сондықтан $с{{tg}x} = a$ теңдеуінің $(0; \pi)$ интервалына бір ғана түбірі бар. Бұл интервалдың ұзындығы π-ге тең. у= ${сtg}x$ функциясының периоды да осы санға тең. Сондықтан ${сtg}x$ = $\ a$ теңдеуінің қалған түбірлері табылған түбірден π n -ге( n- бүтін сан) ерекшеленеді.

Демек, $с{{tg}x} = a$ теңдеуінің шешімі x = arсctg $a$ + π $n$ , мұндағы $\ n -$ бүтін сан, формуласы бойынша табылады, шешімдер жиыны $\left\{ arcсtg\ a\ + \ \pi n, n\mathbb{\in Z}\ \ \right\}$ түрінде жазылады.

5-мысал. ${{сtg}\left( х + \frac{\pi}{4} \right) } = \sqrt{3}$ теңдеуін шешейік.

Шешуі: $х + \frac{\pi}{4}$ = $\ arсctg\ \sqrt{3}\ + \ \pi k, k\mathbb{\in Z}$ ;

$х + \frac{\pi}{4}$ = $\frac{\pi}{6}$ + $\ \pi k, k\mathbb{\in Z}$ ;

x= - $\ \frac{\ \pi}{4} + \frac{\pi}{6} + \pi k, \ k\mathbb{\in Z}$ ;

x= - $\frac{\pi}{12}$ + $\pi k, \ k\mathbb{\in Z}$ .

Жауабы: x= - $\frac{\pi}{12}$ + $\pi k, \ k\mathbb{\in Z}$ .

Негізінде мектеп курсында тригонометриялық теңдеулерді шешуде қандай әдісті қолдану тиімді екендігі жөнінде нақты нұсқаулар жоқ. Бұл жерде таңдау тек мұғалімдердің өз қалауларына байланысты болады. Менің ойымша тригонометриялық шеңберді қолдану тиімдірек болады. Себебі бұл өте көрнекі тәсіл және дәптерде аз орын алады. Негізі қарапайым тригонометриялық теңсіздіктерді шығарған кезде уақыт мүмкіндік беріп жатса екі тәсілді де қолданған жөн. Сонымен айтып кеткенімдей тригонометриялық теңсіздіктеріне тригонометриялық түрлендірулер қолданып оны қарапайым түрге келтіргеннен кейін тригонометриялық шеңбер немесе графикалық әдісті қолданамыз

2. Тригонометриялық теңдеулер және олардың жүйелерін шешуге оқыту

2. 1 Тригонометриялық теңдеулер мен теңсіздіктерді шешуде қажет болатын дағдылар

... жалғасы

Тригонометриялық теңдеулер мен теңсіздіктер, олардың жүйелерін оқыту әдістемесі

Мектеп курсындағы тригонометриялық теңсіздіктерді оқыту әдістемесі

Оқушылардың тригонометриялық теңдеулер мен теңсіздіктерді шешу дағдыларын қалыптастыруға бағытталған техниканы жасау

Жалпы тригонометриялық теңдеулердің түрлерін және оларды шешу жолдарын ашып көрсету

Қарапайым тригонометриялық теңсіздіктер мен теңсіздіктер жүйесін шешу әдістері

Орта мектепте алгебралык тендеулер мен тенсіздіктер такырыптарын окыту әдістемесі

Мектеп математика курсындағы теңдеулер мен теңсіздіктерді оқыту әдістемесі

Мәндес түрлендірулерді теңдеулер шешуге пайдалану

Қарапайым тригонометриялық теңдеулер

Элементар функция

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс