Дискретті кездейсоқ шамалар

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 71 бет
Таңдаулыға:

1-тарау. Орта мектеп математика курсындағы ықтималдық теориясының элементтері

Жалпы білім беретін мектептің 10 сыныптарға арналған матеметикасында кездейсоқ оқиғаның түрлерімен, атап айтақанда, үйлесімсіз оқиғалар мен үйлесімді оқиғалар, тең мүмкіндікті, мүмкін болатын, тәуелсіз және тәуелді оқиғалармен танысып, олардың ықтималдылдығы қандай деген сұрақты қарастырады. Өзгеше айтқанда, кездейсоқ оқиғамен- тәжірибе нәтижесінде пайда болатын оқиғалардың сапалық сипаттамасымен жұмыс жасалынды. Ал, 11 сыныптарда сандық сипаттамалы оқиғалармен танысады. Сандық деп аталғандықтан оқиғаны қандай да бір сандық шама сипаттауы керек. Мысал ретінде, тәуліктің ұзақтығын алсақ ол оның сандық сипаттамасы болады. Бір тәулік ішінде 24 сағаттың бар екені анық, Оны біз тұрақты шама ретінде ала аламыз. Ал адамның жұмыс жасайтын уақытын осы бір тәулік ішінде алсақ, ол өзгеріп кездейсоқ шамаға айналады. [] .

Ықтималдық теориясының негізгі ұғымдары: оқиға және кездейсоқ шамалар ұғымы

Жаңа терминдер: дискретті кездейсоқ шама, кездейсоқ шамаларды қосу, кездейсоқ шама, үзіліссіз кездейсоқ шама, кездейсоқ шамаларды көбейту.

Кездейсоқ шама дегеніміз - мәні кездейсоқ эксперименттердің нәтижесімен анықталатын айнымалы. Жалпы жағдайда эксперименттің әр нәтижесін ассоциация ережесін сүйене отырып, санмен байланыстыруға болады. Санды үлгінің кеңістігінің әр нүктесімен (элементермен) байланыстыру-бұл "үлгіні кеңістіктің нүктелерімен жоғары функциясын анықтау"деп аталатын әдіс. Егер S таңдау кеңістігіндегі ықтималдық өлшемі деп алсақ, ал Х-нақты S элементтерінде анықталған функция болсын. Содан кейін, X кездейсоқ шама деп қарастырамыз. Яғни, Х кездейсоқ шамасы функция болып табылады $A:X = f(A)$ болса, онда $А\ \epsilon\ S$ . X-тің мәні A-да эксперимент нәтижесі қарапайым оқиға болуына байланысты.

Мысал 2. 1

Екі доп кезекпен таңдап алынсын. Қорапта төрте доп бар. Қызыл және үш қара доп. Біз Х кездейсоқ шамасының элементтерін тізімдеп және тиісті X мәндер шамасын ала оырып, жалпы қызыл шарлар санын таңдап аламыз.

Мысал 2. 2

Автокөлікке қатысты мысал қарастырайық:

Үлкен Аккра тіркеу нөмірлі (GR немесе GT) таңдаймыз және

кездейсоқ Х мәнін анықтаймыз

X=1 болады, егер таңдалған автомобиль үлкен Аккра тіркеу нөмірлі болады.

X=0 болады, егер таңдалған автомобиль кішкентай Аккра тіркеу нөмірлері болады. Яғни, егер автомобильде GT 5246 B тіркеу нөмірі болса, онда:

X ( GT 5246 B) = 1

X ( CR 9134 Q ) = 0

X ( WR 2376 D ) = 0

X ( GT 4801 W) = 1

Кездейсоқ шамалар әдетте мәндерінің санына сәйкес жіктеледі. Екі түбегейлі әр түрлі кездейсоқ шамалар дискретті және үздіксіз кездейсоқ шамалар болып екіге бөлінеді.

Дискретті кездейсоқ шама- өз мәндерін тек қана оқшауланған нүктелерде қабылдайтын шама.

Үздіксіз кездейсоқ шама- эксперимент басталғанға дейін мүмкін болатын шама. Кейбір жағдайларда, кез-келген интервал немесе үздіксіз интервал арасындағы сандарды қабылдайды.

Дискретті кездейсоқ шамалар

Анықтама: X айнымалысы эксперимент кезінде $х_{1}, х_{2}, \ldots., х_{к}$ шексіз реттілікпен бір мәнді алады. Егер $х_{к}$ әрбір мәнінде $Р_{к}$ айнымалысының белгілі бір ықтималдығы $х_{к}$ -ке тең мәнін қабылдаған жағдайда, $х_{к}$ дискретті кездейсоқ шама болады.

Яғни, дискретті кездейсоқ шама тек өз мәндерін қабылдайтын айнымалы оқшауланған нүктелерде болады.

Егер X дискретті кездейсоқ шама болса, әрбір x үшін $f(x) \ = \ P(X = x)$ берілген функция X ықтималдықтар диапазонында тарату болып табылады.

Теорема: дискретті кездейсоқ х шамалары және оның $f\ (x)$ мәндері қанағаттандырылған кезде ғана келесі шарттар функция бөлу ретінде қызмет ете алады:

f(x) =0f\ (x) = 0әрбір мән үшін.
∑хf(x) =1\sum_{х}^{}{f\ (x) } = 1жинақтау оның аймағындағы барлық мәндерге қайта таралады.

Сайлау ұйымы облигациялардың белгілі бір шығарылымын ұнататын барлық сайлаушылардың үлесін бағалау үшін 1200 сайлаушыдан жауап алды делік. Сауалнамаға қатысқан 1200 сайлаушының үлесі барлық сайлаушылардың үлесіне жақын болады деп күткен едік, бірақ бұл дұрыс болмауы керек. Сауалнама нәтижесімен байланысты белгілі бір дәрежеде кездейсоқтық бар. Егер сауалнама нәтижелері жоғары ықтималдықпен шынайы пропорцияға жақын болса, онда бізде сауалнама нәтижелеріне сенім бар. Егер ол әсіресе халықтың үлесіне жақын болмаса, онда біз сауалнама нәтижелерін тым байыпты қабылдамауымыз мүмкін. Сауалнамаға қатысқандардың үлесі халықтың үлесіне жақын болу ықтималдығы сауалнама нәтижелеріне деген сенімділігімізді анықтайды. Осы себепті біз бұл ықтималдылықты есептей алғымыз келеді. Оны есептеу міндеті осы тарауда біз зерттейтін ықтималдық аймағына қатысты.

Кәдімгі алтыбұрышты дөңгелектеу кездейсоқ эксперименттің таныс мысалы болып табылады, ол үшін барлық мүмкін нәтижелерді тізімдеуге болады, бірақ кез-келген эксперименттің нақты нәтижесін сеніммен болжау мүмкін емес. Мұндай жағдайда біз әр нәтижеге, мысалы, екі нәтижеге, нәтиженің ықтималдығы деп аталатын санды тағайындағымыз келеді, бұл нәтиженің қаншалықты мүмкін болатындығын көрсетеді. Сол сияқты, біз кез-келген оқиғаға немесе нәтижелер жиынтығына ықтималдылықты тағайындағымыз келеді, мысалы, егер эксперимент жүргізілсе, оқиғаның қаншалықты мүмкін болатындығын көрсететін жұп санды шығару. Бұл бөлім жоғарыда аталған терминдерді қолдана отырып, ықтималдық мәселелерін талқылауға негіз береді.

Анықтама

Кездейсоқ шама - бұл белгілі бір нәтижеге әкелетін механизм, оны сенімді түрде болжау мүмкін емес. Кездейсоқ экспериментке байланысты үлгі кеңістігі барлық мүмкін нәтижелер жиынтығы болып табылады. Оқиға-бұл іріктеу кеңістігінің ішкі жиынтығы.

Егер байқалған нәтиже Е жиынының элементі болса, Е оқиғасы эксперименттің белгілі бір сынағында орын алады деп саналады.

1 мысал. Бір монетаны лақтырудан тұратын эксперимент үшін үлгі кеңістігін жасаңыз.

Шешім:

Нәтижелерді бүркіт үшін h және құйрық үшін t деп атауға болады. Содан кейін үлгі кеңістігі S={H, t} жиынтығы.

2 мысал. Бір мөрді илемдеуден тұратын эксперимент үшін үлгі кеңістігін жасаңыз. Табыңыз оқиғалар, тиісті фразам "домалап барады четное число" және "домалап барады саны екі". ”

Шешім:

Нәтижелер матрицаның жоғарғы бетіндегі нүктелер санына сәйкес белгіленуі мүмкін. Содан кейін үлгі кеңістігі s={1, 2, 3, 4, 5, 6} жиынтығы болып табылады.

Жұп нәтижелер 2, 4 және 6 - ға тең, сондықтан "жұп сан айналады" деген тіркеске сәйкес келетін оқиға {2, 4, 6} жиынтығы болып табылады, оны E әрпімен белгілеу табиғи.

Сол сияқты, "екіден Үлкен сан" тіркесіне сәйкес келетін оқиға - бұл t={3, 4, 5, 6} жиынтығы, біз оны t деп белгіледік.

Үлгі кеңістігі мен оқиғалардың графикалық көрінісі суретте көрсетілгендей Венн диаграммасы болып табылады. 3. 1" 1-мысал "3. 6-ескертпесі және" 2-мысал "3. 7-ескертпесі үшін" іріктеменің екі кеңістігі үшін Венн диаграммалары". Жалпы жағдайда s үлгісінің кеңістігі тіктөртбұрышпен, нәтижелері тіктөртбұрыштың ішіндегі нүктелермен, ал оқиғалар оларды құрайтын нәтижелерді қамтитын аналық бездермен ұсынылған.

Сурет. 3. 1 екі үлгі кеңістігі үшін Венн диаграммалары

3 мысал. Кездейсоқ эксперимент екі тиынды лақтырудан тұрады.

Монеталарды екі жаңа пенни сияқты ажыратуға болмайтын жағдай үшін үлгі кеңістігін жасаңыз. Монеталар бір тиынға, ал екіншісі никельге ұқсамайтын жағдайға үлгі кеңістігін жасаңыз.

Шешім:

Монеталар лақтырылғаннан кейін, 2h таңбалауға болатын екі бас, 2T таңбалауға болатын екі құйрық немесе d таңбалауға болатын әр түрлі монеталар бар.

Монеталарды бір-бірінен ажырата алатындықтан, монеталарды ажыратудың екі әдісі бар: Пенни бастары мен никель құйрықтары немесе Пенни құйрықтары мен никель бастары. Біз әр нәтижені екі әріппен белгілей аламыз, олардың біріншісі Пеннидің қалай қонғанын, ал екіншісі никельдің қалай қонғанын көрсетеді. Содан кейін үлгі кеңістігі S'={һһ, ht, th, tt}.

Кездейсоқ эксперименттің барлық мүмкін нәтижелерін анықтауға пайдалы болуы мүмкін, әсіресе кезең - кезеңмен қарастыруға болатын құрылғы-бұл ағаш диаграммасы деп аталады. Бұл келесі мысалда сипатталған.

4 мысал. Үш баласы бар барлық отбасыларды туу тәртібіне сәйкес балалардың жынысына сәйкес сипаттайтын таңдау кеңістігін құрыңыз.

Шешім:

Екі нәтиже - bbg-ді білдіретін "екі ұл, содан кейін қыз" және gbb-ді білдіретін "қыз, содан кейін екі ұл". Әрине, көптеген нәтижелер бар, және біз олардың барлығын тізімдеуге тырысқанда, егер біз жүйелі түрде әрекет етпесек, олардың барлығын тапқанымызға сенімді болу қиын болуы мүмкін. Суретте көрсетілген ағаш диаграммасы. 3. 2" үш баласы бар отбасыларға арналған ағаш диаграммасы " жүйелі тәсіл ұсынады.

Сурет 3. 2. Үш баласы бар отбасыларға арналған ағаш диаграммасы

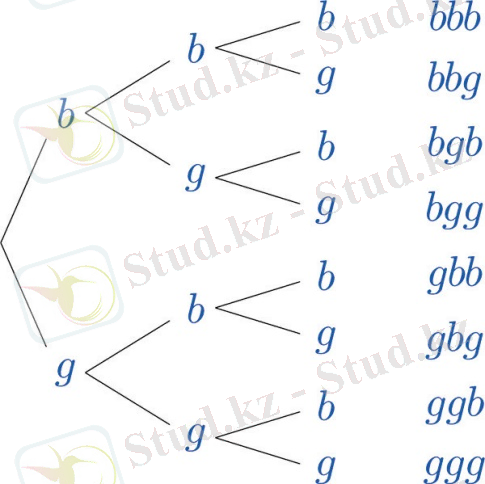
Схема келесідей жасалды. Бірінші балаға, ұлға немесе қызға екі мүмкіндік бар, сондықтан біз бастапқы нүктеден шығатын екі сызықты сызамыз, олардың біреуі "ұлға" арналған в әрпімен, ал екіншісі "қызға"арналған g әрпімен аяқталады. "Бірінші бала үшін осы екі мүмкіндіктің әрқайсысы үшін екінші балаға, " ұлға "немесе" қызға " екі мүмкіндік бар, сондықтан В және Г-ның әрқайсысынан біз екі сызық кесіндісін тартамыз, бір сегмент В-да және біреуі g-де аяқталады. диаграммадағы төрт соңғы нүктенің әрқайсысы үшін қазір үшінші бала үшін екі мүмкіндік бар, сондықтан біз процесті тағы бір рет қайталаймыз.

Сызық сегменттері ағаш бұтақтары деп аталады. Әр тармақтың оң жақ соңғы нүктесі түйін деп аталады. Оң жақ бұрыштағы түйіндер соңғы түйіндер болып табылады; суретте көрсетілгендей олардың әрқайсысы нәтижеге сәйкес келеді.

Ағаштан тәжірибенің сегіз нәтижесін оқу оңай, сондықтан үлгінің кеңістігі-бұл ағаштағы соңғы түйіндерді жоғарыдан төменге қарай оқу,

S={bbb, bbg, bgb, bgg, gbb, gbg, ggb, ggg}

Ықтималдық анықтамасы

Үлгі кеңістігіндегі e нәтижесінің ықтималдығы S-0 мен 1 арасындағы p саны, ол тиісті кездейсоқ эксперименттің бір сынағында e болу ықтималдығын өлшейді. P = 0 мәні e нәтижесінің мүмкін еместігіне сәйкес келеді, ал p = 1 мәні e нәтижесінің сенімділігіне сәйкес келеді.

Анықтамасы

А оқиғасының ықтималдығы-бұл оның құрамына кіретін жеке нәтижелердің ықтималдығының қосындысы. Ол P(A) деп белгіленеді.

Келесі формула оқиғаның ықтималдығын анықтау мазмұнын білдіреді:

Егер Е оқиғасы E={e1, e2, . . . , ek} болса, содан кейін

P(E) =P( $e_{1}$ ) + P( $e_{2}$ ) + … + P( $e_{k}$ )

Сурет. 3. 3" таңдамалы кеңістіктер және ықтималдық " анықтамалары графикалық түрде суреттелген.

Сурет. 3. 3 үлгі кеңістігі және ықтималдық

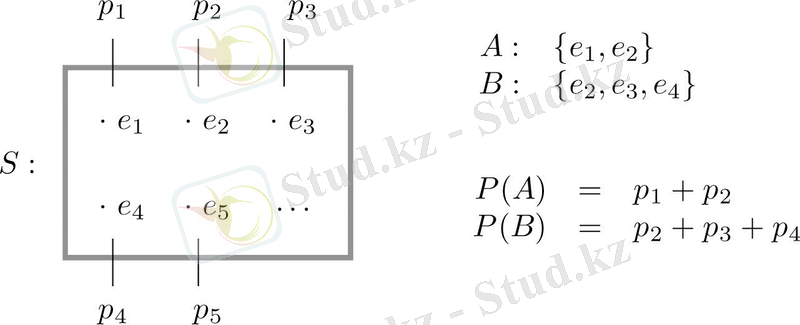
Барлық s үлгі кеңістігі міндетті түрде болатын оқиға болғандықтан, барлық нәтижелердің ықтималдық қосындысы 1 саны болуы керек.

Кәдімгі тілде ықтималдықтар көбінесе пайызбен көрсетіледі. Мысалы, біз ертең жаңбырдың ықтималдығы 70% құрайды деп айтамыз, яғни жаңбырдың ықтималдығы 0, 70 құрайды. Біз бұл тәжірибені осы жерде қолданамыз, бірақ барлық кейінгі есептеу формулаларында 70% емес, 0. 70 нысанын қолданамыз.

5 мысал. Монета "теңдестірілген" немесе "әділ" деп аталады, егер әр тарап бірдей ықтималдылықпен қонса. Эксперимент үшін үлгі кеңістігіндегі әр нәтижеге ықтималдылықты тағайындаңыз, ол бір адал монетаны лақтырудан тұрады.

Шешім:

Бүркіт үшін h және құйрық үшін t деп белгіленген нәтижелермен үлгінің кеңістігі S={H, t} жиынтығы болып табылады. Нәтижелер 1-ге дейін жиналуы керек бірдей ықтималдылыққа ие болғандықтан, әр нәтижеге 1/2 ықтималдығы беріледі.

6 мысал. Егер екі жағы бірдей ықтималдылықпен жоғарыдан қонса, текше "теңдестірілген" немесе "әділ" деп аталады. Эксперимент үшін үлгі кеңістігіндегі әр нәтижеге ықтималдылықты тағайындаңыз, ол бір адал текшені лақтырудан тұрады. E оқиғаларының ықтималдығын табыңыз: "жұп сан айналады "және T:" екіден Үлкен сан айналады. ”

Шешім:

Матрицаның жоғарғы бетіндегі нүктелер санына сәйкес белгіленген нәтижелермен іріктеу кеңістігі s={1, 2, 3, 4, 5, 6} жиынтығы болып табылады. 1 болуы керек алты бірдей нәтиже болғандықтан, әрқайсысына 1/6 ықтималдығы беріледі.

Себебі E={2, 4, 6}, P (E) =1∕6+1∕6+1∕6=3∕6=1∕2.

Себебі T = {3, 4, 5, 6}, P (T) =4∕6=2∕3.

7 мысал. Екі адал монета лақтырылады. Монеталардың сәйкес келу ықтималдығын табыңыз, яғни жердің екі басы да, жердің екі құйрығы да.

Шешім:

3. 8 "3-мысал" жазбасында біз монеталар бірдей болатын жағдай үшін S={2h, 2T, D} және екі монетаны ажыратуға болатын жағдай үшін S'={HH, ht, th, TT} үлгі кеңістігін салдық.

Ықтималдық теориясы нәтижелерге ықтималдылықты қалай тағайындау керектігін, олар тағайындалған кезде олармен не істеу керектігін айтпайды. Атап айтқанда, s үлгі кеңістігін қолдана отырып, сәйкес келетін монеталар-бұл P(2h) +P(2t) ықтималдығы бар m={2h, 2t} оқиғасы. S 'таңдау кеңістігін қолдана отырып, сәйкес келетін монеталар-бұл P(hh) +P(tt) ықтималдығы бар m'={HH, TT} оқиғасы. Физикалық әлемде монеталардың бірдей немесе бірдей емес екендігі маңызды емес, сондықтан біз P(M) және P(M') сандары бірдей және нақты физикалық тәжірибелер әділ болып көрінетін монеталармен жүргізілген кезде байқағанымызға сәйкес келетін нәтижелерге ықтималдық бергіміз келеді. Нақты тәжірибе көрсеткендей, s ' нәтижелері бірдей ықтимал, сондықтан біз әр ықтималдылықты 1∕4, содан кейін тағайындаймыз

P(M') =P(hh) +P(tt) =14+14=12

Сол сияқты, тәжірибеге сүйене отырып, s нәтижелері үшін тиісті нұсқалар:

P(2h) =14 P(2t) =14 P(d) =12

олар бірдей нақты жауап береді

P(M) =P(2h) +P(2t) =14+14=12

Алдыңғы үш мысал іріктеу кеңістігі бірдей ықтимал нәтижелердің соңғы санынан тұратын кезде ықтималдылықты қарапайым есептеу арқылы қалай есептеуге болатындығын көрсетеді. Кейбір жағдайларда экспериментті білдіретін кез-келген үлгі кеңістігінің жеке нәтижелері сөзсіз біркелкі емес, және бұл жағдайда ықтималдылықты санау арқылы есептеу мүмкін емес, бірақ оқиғаның ықтималдығын анықтауда берілген есептеу формуласын қолдану керек.

8 мысал. Жергілікті орта мектепте оқушылардың нәсілі мен ұлты бойынша таралуы 51% ақ, 27% қара, 11% латындар, 6% азиялықтар және 5% басқалар үшін. Оқушы Осы орта мектептен кездейсоқ таңдалады. ("Кездейсоқ" таңдау әр оқушының таңдалу мүмкіндігі бірдей екенін білдіреді. ) Келесі оқиғалардың ықтималдығын табыңыз:

Б: студент қара,

М: студент-азшылық (яғни, АҚ емес),

Н. : Студент қара емес.

Шешім:

Эксперимент-бұл орта мектеп оқушыларының арасынан оқушыны кездейсоқ таңдау әрекеті. Үлгінің айқын кеңістігі-S = {W, b, h, a, o}. Студенттердің 51% - ы АҚ болғандықтан және барлық студенттердің таңдалу мүмкіндігі бірдей болғандықтан, P(w) =0, 51 және басқа нәтижелерге ұқсас. Бұл ақпарат келесі кестеде келтірілген:

Нәтиже

w b h a o

Нәтиже: Ықтималдық

w b h a o: 0. 51 0. 27 0. 11 0. 06 0. 05

B = {b} болғандықтан, P (B) = P (b) = 0, 27.

M = {b, h, a, o} болғандықтан, P (M) = P (b) + P (h) + P (a) + P (o) = 0. 27 + 0. 11 + 0. 06 + 0. 05 = 0. 49

N = {w, h, a, o} болғандықтан, P (N) = P (w) + P (h) + P (a) + P (o) = 0. 51 + 0. 11 + 0. 06 + 0. 05 = 0. 73

9-мысал. 3. 18 ескертуінде қарастырылған орта мектептегі студенттер қауымдастығы «8-мысал» он санатқа бөлінуі мүмкін: 25% ақ ер, 26% ақ әйел, 12% қара ер, 15% қара әйелдер, 6% испандық ерлер, 5% испандық әйелдер, 3% азиялық ерлер, 3% азиялық әйелдер, 1% басқа азшылықтардың еркектері және 4% басқа азшылықтардың әйелдері. Студент осы орта мектептен кездейсоқ таңдалады. Келесі оқиғалардың ықтималдығын табыңыз:

B: студент қара,

MF: студент азшылық әйелдер,

FN: студент әйел, қара нәсілді емес.

Шешім:

Енді үлгі кеңістігі S = {wm, bm, hm, am, om, wf, bf, hf, af, of} құрайды. Мысалда келтірілген ақпаратты екі жақты төтенше жағдай кестесі деп аталатын келесі кестеде келтіруге болады:

Жыныс

Нәсіл / этнос

Ақ

қара

испандық

азиялықтар

өзгелер

Жыныс: Ер

Нәсіл / этнос: 0, 25

: 0, 12

0, 06

0, 03

0, 01

Жыныс: Әйел

Нәсіл / этнос: 0, 26

: 0, 15

0, 05

0, 03

0, 04

B = {bm, bf} болғандықтан, P (B) = P (bm) + P (bf) = 0, 12 + 0, 15 = 0, 27.

MF = {bf, hf, af, of} болғандықтан, P (M) = P (bf) + P (hf) + P (af) + P (of) = 0. 15 + 0. 05 + 0. 03 + 0. 04 = 0. 27

FN = {wf, hf, af, of} болғандықтан, P (FN) = P (wf) + P (hf) + P (af) + P (of) = 0, 26 + 0, 05 + 0, 03 + 0, 04 = 0, 38

Математика тек формулалар мен идеялар ғана емес. Ол қазіргі заманғы өмірде қолдану облыстарын табады. Ол медицинаға дейін немесе табиғатты қорғаудан қаржыға дейін бізді қоршаған әлем инженериясына математикалық модельдеу айтарлықтай үлес қосады.

Сіз балалық шақта ойнаған пойыздың моделін қарастырыңыз. Моделі бұл нақты пойыздың жеңілдетілуін білдіреді (ол кішірек, адам жоқ жүргізуші және т. б. ), бірақ оның жалпы қасиеттері бар (ол рельстерде жұмыс істейді, ол электрмен қоректене алады және ұқсас пішінге ие болуы мүмкін) .

Пойызбен ойнау арқылы сіз пойыздар туралы барлық фактілерді біле аласыз: олар көтеріле алатын беткейлер: вагондардың саны жылдамдыққа қалай әсер етеді, рельстен шығу немесе апаттың салдары қандай болуы мүмкін.

Сол сияқты, егер біз нақты математикалық модель жасасақ әлемдік жағдай, біз нақты жағдайды талдау арқылы математикалық моделін біле аламыз. Біз нақты мәселелерді де нақты өмірде тест құруға байланысты шығындар немесе қауіптер жоқ деп шеше аламыз.

Математикалық модель- бұл әлемдегі нақты жағдайды жеңілдету. Оны нақты мәселені болжау үшін пайдалануға болады. Осы модельдің көмегімен жағдайды жақсы түсінуге болады. Модель Нақты жағдайдың кейбір, бірақ барлық ерекшеліктерін ескеруге бағытталған. Белгілі бір болжамдар және бұл модель барлық ерекшеліктерді көрсетпейтінін білдіруі мүмкін нақты жағдай қажет. Математикалық модельдер пайдалы, себебі:

олар тез және оңай жасалады;
олар қиын жағдайды жеңілдетуі мүмкін;
олар бізге нақты әлем туралы түсінігімізді жақсартуға көмектеседі, өйткені кейбір айнымалылар өзгерту оңай;
олар сізге болжам жасауға мүмкіндік береді;
олар бақылауды қамтамасыз етуге көмектеседі.

Математикалық модельдерге кейде сақтықпен қарау керек, өйткені:

модель нақты мәселені жеңілдету болып табылады және барлық мәселелері аспектілерді қамтымайды;
модель белгілі бір жағдайларда ғана жұмыс істей алады.

Мысал ретінде мына жағдайға назар аударайық. Фермер тауық етін сатып алғысы келеді. Ол аптасына қанша жұмыртқа салынады деп сұрайды. Сатушыда ол қолдана алатын үш шара бар. Ол мүмкін аптасына сегіз жұмыртқа санын келтіріңіз, бұл орташа, аптасына 8, 2 жұмыртқа, бұл орташа немесе 10 аптасына жұмыртқа, бұл режим. Қандай шараны сатушы көрсетуі керек пе? Статистикада сіз кез-келген айнымалыға бақылау немесе өлшеу жинайсыз. Мұндай бақылаулар деректер ретінде белгілі. Сандық бақылаулармен байланысты айнымалылар сандық айнымалылар деп аталады. Сандық емес бақылаулармен байланысты айнымалылар сапалық айнымалылар деп аталады.

Мысал. Кестедегі айнымалылардың әрқайсысы үшін олардың бақылаулары сандық немесе жоқ екенін көрсетіңіз.

Айнымалы

Бақылау

: 1

Айнымалы: Жаға өлшемі

Бақылау: 14, 14