Мектепте дифференциалдық теңдеулерді факультатив сабақтарда оқытудың теориялық-әдістемелік негіздері


КІРІСПЕ
Қазіргі кездегі мектеп бағдарламасында дифференциал теңдеулер туралы мағлұматтар беріледі. Атап айтқанда, дифференциал теңдеулер деген не, оның шешімі және олардың математикалық, физикалық және техникалық есептерді шығаруға қолданылуы т. б.
Қазіргі қоғамның әлеуметтік сұраныстарына байланысты мектеп бағдарламасына енгізілген дифференциалдық теңдеулер теориясы ғылымының әртүрлі облыстарында кеңінен қолданылады.
Оқушыларға жоғары алгебра элементтері бар есептерді теориялық негізде әзірлеп, жалпы орта білімді мектептердегі әдістеменің базисын құру жолдарына талдау жасау.
Жалпы орта білімді мектептерде жоғары алгебра элементтерін мектеп курсында оқытудың әдістемесі - оқушыларды оқытудағы негізгі орта білім деңгейімен және жоғары білім арасындағы сабақтастық пен болашақты қамтамасыз ететін оқыту әдісі болып табылады. Алгебра және анализ бастамалары курсымен орта мектептегі алгебраны оқыту аяқталады. Бұл жұмыс анализ бастамаларына қатысты ұғымдарды, тұжырымдар мен әдістерді мазмұндық ашумен, оқушылардың ой-өрісін, логикалық пайымдау, дәлелдеулер жүргізу, практикалық есептерді шығару барысында жоғары алгебра элементтері білімдерін қолдану біліктігін дамытуға бағытталған; математикалық оқу қызметіне оқушыларды қатыстыруға, олардың жоғары алгебраның кейбір элементері бар материалды түсінуіне бағытталған жұмыстардың белсенді түрлерін көбейтуді көздейді.
Айнымалылары ажыратылатын қарапайым дифференциалдық теңдеу теңіз деңгейінен биіктігіне байланысты атмосфералық қысымның өзгеру процессін де, радийдің түсу процесін де, тұрғындар санының өзгеру процессін де, суыту процесін де және т. б. сипаттайды.
Дипломдық жұмыс тақырыбының өзектілігі:
- математикалық талдау және дифференциалдық теңдеулер негізінен болашақ студенттердің математикалық біліміне үлкен үлес қосады.
- дифференциалдық теңдеулер мектептің математика курсында оқытудың әдістемесіне арналған зерттеулердің кемдігі.
Дипломдық жұмыс тақырыбының ғылыми жаңашылдығы және практикалық маңыздылығы: Дифференциалдық теңдеулер теориясының мазмұны абстрактылы - теориялық ойлауды, шығамашылық қабілетті жетілдіруді керек етеді және соған жетелейді. Жетілдіре оқытудың маңызды құрамының бірі ретінде оқушылардың танымдық, шығармашылық ойлау қабілетін жандандыру саналады.
Сонымен қатар игерілетін материалдың математикалық қабілетін қарқынды дамытатын, оларға терең тәрбиелік ықпалын тигізетін ұстанымдардың да маңызы айырықша.
Ғылыми мәселенің ағымдағы жағдайы: дифференциалдық теңдеулерді оқу қиял ойдың дамуына нәр береді, оқушыларға дифференциалдық теңдеулердің абстрактілігі табиғат құбылыстарын математикалық модельдер көмегімен оқып білудің құралы болып табылады.
Дифференциалдық теңдеулер болашақ студенттің фундаметальды дайындығында, атап айтқанда оқушының ғылыми дүниетанымын, математикалық мәдениетінің белгілі бір дәрежесін қалыптастыруда үлкен роль атқарады.
Диплом жұмысының мақсаты: осы пән туралы мағлұмат беру және қарапайым теңдеулерді шығару жолдарын көрсету.
Мектеп курсында дифференциал теңдеулерге сағат аз болғандықтан біз мұнда негізгі анықтамалар мен ұғымдарды беріп, соларға көптеп мысалдар келтірумен шектелеміз. Дифференциалдық теңдеулерді оқыту мазмұны мектептерде математиканы оқытуда қосымша, дарынды оқушыларымен жұмыс ретінде қарастыру.
Диплом жұмысының міндеттері:
- дифференциалдық теңдеулер теориясының мазмұны абстрактылы - теориялық ойлауды;
- шығармашылық қабілетті жетілдіруді;
- оқытудың маңызды құрамының бірі ретінде оқушылардың танымдық, шығармашылық ойлау қабілетін жандандыру;
- сонымен қатар игерілетін материалдың математикалық қабілетін қарқынды дамытатын, оларға терең тәрбиелік ықпалын тигізетін ұстанымдардың да маңызы айырықша.
Дипломдық зерттеудің объектісі; алгебра және анализ бастамалары, математикалық анализ курсы
Диплом жұмысының теориялық және әдіснамалық негіздері: Қазақстан Республикасы «Білім туралы» заңы, мемлекеттік білім беру стандарттары, математиканы оқытудың теориялық және әдістемелік негіздері, алгебра және анализ бастамалары.
Есептерді шығаруда табылған жалпы шешімдер қарапайым, сапалы талдау жүргізуге, модельдің орнықты шешімдері мен құрылғының жұмысындағы «орнатылған тәртіптің» нақты сипаты арасында сәйкестік орнатуға болады.
Дифференциалдық теңдеулер мен олардың әдістерін оқып үйрену біз өмір сүретін әлемді тану үшін тағы бір құралды береді, яғни нақты физикалық кеңістік туралы бейнелік және ғылыми түсінікті қалыптастыруға мүмкіндік береді.
Дипломдық жұмыс жазылуының тәжірибелік базасы: Арқалық қалалық кітапханасы. Ы. Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты кітапханасы.
- ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ФАКУЛЬТАТИВ САБАҚТАРДА ОҚЫТУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ
1. 1 Дифференциалдық теңдеулердің математикада алар орны
Дифференциалдық теңдеу негізгі математикалық ұғымдардың бірі болып табылады. Дифференциалдық теңдеу - бұл туындыларды (немесе дифференциалдары) қандайда бір алдынала берілген шарттарды қанағаттандыратын теңдеу. Қандайда бір нақты құбылыс пен процессті зерттеудің нәтижесінде алынған дифференциалдық теңдеу дифференциалдық модель деп аталады.
Дифференциалдық модельдер - бірі бізді қоршаған әлемді оқып үйренуде құрылуы мүмкін математикалық модельдер жиынының дербес жағдайы екені түсінікті. Сонымен қатар, дифференциалдық модельдердің өздерінің де түрлі типтері бар екенін атап өту қажет. Біз бұл жұмыста тек қарапайым дифференциалдық теңдеулермен сипатталатын модельдерді ғана қарастырамыз, оларға тән ерекшеліктердің бірі бұл теңдеулердегі белгісіз функциялар тек бір ғана айнымалыға тәуелді болады.
Қарапайым дифференциалдық модельдерді құру процесінде зерттеліп жатқан есептің табиғатына қатысты ғылым заңдарын білу маңызды және алдыңғы мәнге ие. Мысалға, механикада бұл Ньютонның заңдары, ал электрлік тізбектік теориясында - Кирхгоф заңдары, химиялық реакциялардың жылдамдығы теориясында - салмақтың әсер ету заңы және т. б.
Әрине іс жүзінде дифференциалдық теңдеулерді құруға мүмкіндік беретін белгісіз заңдарды да кездестіруге болады, сондықтан параметрлердің - айнымалылардың аз өзгерісінде процесстің жүруіне қатысты әртүрлі жорамалдарға (гипотезаларға) сүйену қажет. Онда дифференциалдық теңдеулерге шектік ауысу келтіреді. Мұнда, егер математикалық модель ретінде алынған дифференциалдық теңдеуді зерттеу нәтижесі тәжірибелік берілгендермен сәйкес келсе, онда тұжырымдалған гипотеза заттардың шынайы күйін дұрыс көрсететінін білдіреді [1] .
Кейбір жағдайларда ғана дифференциалдық теңдеулерді тұйық форма деп аталатын түрде шығаруға, яғни элементар функциялармен қарапайым операциялардың шектеулі санын пайдаланатын шешімді аналитикалық формула түрінде көрсетуге болады. әрине, бұл дифференциалдық теңдеулердің шешімі бар екені белгілі болған кезде.
Басқаша айтқанда, дифференциалдық теңдеулердің шешімдері өздерінің көптүрлілігімен мынадай, олардың саны шектеулі аналитикалық операциялармен тұйық формада көрсету үшін жеткіліксіз. Бұл жағдай алгебралық теңдеулер теориясындағыға ұқсас: бірінші және екінші дәрежелі алгебралық теңдеулер жағдайында олардың шешімдері радикалдарда оңай алынуы мүмкін; егер үшінші және төртінші дәрежелі теңдеулерге келсек, онда радикалдардағы шешімдер алынуы мүмкін, бірақ формалар едәуір қиын болады; ал дәрежесі төрттен жоғары жалпы түрдегі алгабралық теңдеулерді қарастырсақ, онда бұндай теңдеулердің радикалдардағы шешімдерді, жалпы айтқанда, алынуы мүмкін емес.
Дифференциалдық теңдеулердің шешімдерін көрсету үшін қандай да бір түрдегі шексіз қатарларды пайдалансақ, онда тұйық формалардағыға қарағанда едеуір көп теңдеуді шешуге тура келеді. Бірақ, шешімнің орынды және тиімді қасиеттерін, алынған қатар түрінен анықтау еш мүмкін емес. Сонымен қатар, тіпті дифференциалдық теңдеуді тұйық формада шығара алсақ та, мұндай шешімді талдау мүмкін емес, немесе әр түрлі параметрлер арасындағы тәуелділік өте қиын болып шығады.
Осылайша, дифференциалдық теңдеулердің өзін шығармай-ақ шешімдердің қайсыбір қасиеттері туралы қажетті мағлұматтар алуға мүмкіндік беретін әдістер мен тәсілдердің қажеттілігі анық болып отырады. Мысалыға, бұндай әдістер мен тәсілдер бар және олар дифференциалдық теңдеулердің сапалық теориясының мазмұнын құрайды, олардың негізінде шешімдердің бар болуы мен жалғыз болуы, шешімнің бастапқы берілгендер мен параметрлерге үзіліссіз тәуелділігі туралы жалпы теориялар жатыр.
Қарапайым дифференциалдық теңдеудің сапалық теориясы А. Пуанкаре мен А. М. Ляпуновтың (ХІХ-шы ғасырдың соңы) жұмыстарынан бастап дамып келеді және оның әдістері бізді қоршаған ортаны тану процессінде кең қолданылады [2] .
1. 2 Дифференциалдық теңдеулерді мектепте оқытудың педагогикалық - психологиялық негіздері
Мектептегі математика курсының негізгі мақсаттарының бірі оқушыларды ғылыми дүниетанымға тәрбиелеу деп есептелінеді. Жоғарыда аталған мақсатты жүзеге асыру мағынасында дифференциалдық теңдеулер тақырабы тиімді.
Қазіргі заманда, жалпы мойындаған жағдай математиканы оқытудың кез келген сатысында (мектепте, лицейде, колледжде, ЖОО-да және т. б. ) әрдайым методология, философия, тарих, яғни оқытудың методологиялық аспекті деп аталатындарды құрайтындармен байланыстыру қажет. Бұл аспект дербес шығуы мен дамуы, математиканың тарихи даму процесінде оқушының ойында әрқашан нақтыланып және кеңейіп отыратын оның зерттеу пәнінің анықтамасы, математиканың нақты өмірмен, адамдардың қоғамдық іс-әрекетімен байланысы, іс-тәжірибенің математикадағы ролі және ең соңында қазіргі заманғы ғылыми білімнің математизациялану мағынасының ашылуымен байланысты мәселелерді әрдайым талқылау қажеттілігі енеді.
Оқушыларды рухани дамыта отырып, олардың әлемге деген іс-тәжірибелік көзқарастың негізі ретінде ғылыми дүниетанымды қалыптастыру қажет. Олар математиканың жалпы ұғымдарының нақты әлемнің белгілі бір бейнелерін көре білуі, математикаға редукцияланған философияның негізгі сұрағына дұрыс жауап бере алуы керек.
Математикалық - жаратылыс ғылымдарының матедологиясының дифференциалдық теңдеулермен тұтас байланысын, дифференциалдық теңдеулердің матодологиялық бағытын көрсететін дифференциалдық теңдеулер теориясының даму тарихын қарастырамыз. Негізінен дифференциалдық теңдеулер теориясына Россия, Қазақстан және басқа ТМД елдерінің ғалымдарының үлесі үлкен.
Оқушылардың ғылыми дүниетанымын және жалпы мәдениетін қалыптастыруға осы пәнді оқытудың қолданбалы бағыты, оны дұрыс ұйымдастырғанда, яғни оқытудың жалпы принциптерінің - оқытудың өмірмен, теорияның практикамен байланысы принциптерінің бірін орындағандағы ұйымдастыруда, орынды үлес қосады [3] .
Математиканы оқытудың қолданбалы бағытының мәселесі математиктер мен әдіскерлердің зеттеулерінде кең қарастырылған. Оның теориялық негізделуі В. Г. Болтянскийдің, Е. С. Венцельдің, А. Н. Колмогоровтың, А. Н. Тихоновтың, З. И. Халиловтың, Д. П. Костомарованың, Ю. М. Колягиннің, В. М. Монахованың, В. А. Гусевтің, С. И Швацбурдтың, В. В. Фиреовтың, Г. В. Дрофееваның, М. И. Башмакованың, И. Д. Шарышнаның, К. К. Пономареваның, Н. Я. Виленкинаның, А. Д. Мышкистің, Л. Д. Кудрявцевтің, Г. Трелиньски, В. В. Амелькинаның, А. П. Садовскийдің, И. И. Бавриннің, А. В. Латышеваның, Н. А. Тереишнаның, М. С. Сабурованың және т. б. жұмыстарында келтірілген.
Жоғарыда аталған авторлардың барлығы математиканы мектепте оқытудың қолданбалы бағыттағы мәселелерін зерттейді.
Б. А. Найманов өзінің кандидаттық диссертациясында дифференциалдық теңдеулердің қолданбалы бағыттының үш компонентін атап өтеді.
- абстрактілі ұғымдар мен теориялық білімдерді нақтылау;
- математиканың теориялық мәселерінің математикалық теорияның қосымшаларымен өзара байланысы.
- студенттерге оқушыларды математиканың қолданбалы бағытымен таныстыру тәсілдерін оқыту.
Оқыту процессінде қолданбалы мәселелерді пайдалану тек қана ғылымның негіздерін түсінуге емес, ғылыми танымның тәсілдерін меңгеругеде әсер етеді.
Дифференциалдық теңдеулердің қолданбалы бағытынан оқушы нақты процесті математикалық модельдермен байланыстыру тәжірибесін алады.
Нақты процесстің математикалық моделі деп, әдетте, бұл процес математика тілінде жуықтап сипатталуын түсінеміз.
Математикалық модельдеу өнері нақты есепті математикалық тілге аудара білуден тұрады.
Матетикалық модельдеу өзінің қарапайымдылығымен процесті жақсы түсінуге көмектесді, процестің қалпының сапалық және сандық сипатын орнатуға мүмкіндік береді.
Әр түрлі есептерде нақты процестердің математикалық моделі көбіне дифференциалдық теңдеулермен өрнектеледі [4] .
Бұл есептердің сипаты мен шығару әдістемесін схемалық түрде сипаттауға болады. Қандай да бір процесс жүріп жатыр делік, мысалы, физикалық, химиялық, биологиялық. Бізді бұл процестің белгілі бір функционалдық сипаттамасы, мысалы, уақытқа қатысты температураның немесе қысымның, массаның, кеңістіктегі қалпының өзгеру заңдылығы қызықтырады. Егер бұл процестің жүруі туралы толық ақпарат бар болса, онда оның математикалық моделін құруға әрекет жасауға болады. Көп жағдайларда бұндай модель дифференциалдық сипаттамасы болып табылады. Дифференциалдық теңдеу, процестің эволюциясын материалдық жүйемен болып жатқан өзгерістер сипатын, бұл
жүйе өзгерістерінің бастапқы күйін байланыстыратын нұсқауларды сипаттайды.
Кез келген процесті оқып үйрену оның жеке моменттерін анықтау мен оның ағымының жалпы заңын орнатуға келіп тіреледі.
Процесстен (қарапайым процесстің) жеке моменттегі процестің айнымалы шамаларын олардың дифференциалдарды және туындыларымен байланыстыратын дифференциалдық теңдеулермен өрнектеледі. Интегралдаудан кейін алынатын құбылыстың жалпы орындалу заңдылығы процестің айнымалы шамаларын байланыстыратын теңдеумен өрнектеледі.
Дифференциалдық теңдеулерді құрудың қатаң тәртібі жоқ. Көптеген жағдайларда қарапайым дифференциалдық теңдеулерді қолданумен байланысты қолданбалы есептерді шығарудың әдістемесі келесіге келтіріледі:
- есептің шартын талдап, оның мәнін айқындайтын сызбаны салу;
- қарастырылып отырған процестің дифференциалдық теңдеуін құру;
- осы теңдеуді интегралдап, оның жалпы шешімін анықтау;
- берілген бастапқы шарттардың негізінде есептің дербес шешімін анықтау;
- қажет болған жағдайда көмекші параметрлерді (мысалы, пропорционалдық коэффициентін және т. б. ) анықтау, бұл мақсат үшін есептің қосымша шарттары пайдаланылады;
- қарастырылып отырған процестің жалпы заңын тұжырымдау және ізделінді шамалардың сандық мәнін анықтау;
- жауапты талдау және есептің бастапқы қалпын тексеру.
Модельдеу икемділігі танымдылық іс-әрекеттің ажыратылмас бөлігі болып табылады. Модельдеудің психологиялық аспектісі, адам санасында сыртқы әлемді оның көптүрлілігі мен ішкі және сыртқы байланыстарның толықтығында емес, тұрпайыланған жуық түрде бейнелеуден тұрады.
Біз нақты құбылыс туралы сезіну мен түсіну арқылы алатын толық емес ақпарат біздің санамызда толық емес түрде елестетулер мен бейнелер жүйесі ретінде қалыптасатындар негізіне құбылыстың модельдері болып табылады. Сондықтан, біздің қоршаған әлем туралы түсінігіміз принципиалды модельды сипатқа ие.
Соңғы жылдары психикалық іс әрекеттің жемісі ретінде модельдің мәні сезілуде. Сонымен қатар модель мидың құбылысы ретінде әр түрлі аспектілірде қарастырады. Бірқатар ғалымдар модельді адамның қоршаған ортамен қатынасындағы психикалық іс-әрекетінің негізгі жемісі ретінде қарастырылады. Кейбір зерттеушілер оқытудағы модельдеуге үлкен роль бөлетіні соншалық оны жеке принципке бөледі. Мысалы, В. В. Давыдов традициялық дидактикалық көрнектілік принципінің шектеулілігін, оны модельдеу принципімен алмастыруды ұсынады.
Л. М. Фридман, В. В. Давыдовтың орта мектепте математиканы оқытудағы модельдің тәсіл идеясын дамытып, былай деп жазады:
« . . . математиканы оқытудағы модельдеу принципі, біріншіден, мектеп курсындағы математика мазмұнын модельдік көзқараспен меңгеруді, екіншіден, оқушыларда әртүрлі құбылыстар мен жағдайларды математикалық модельдеу біліктілігі мен икемділігін қалыптастыруды, үшіншіден, ішкі ойды, ойлаудың ғылыми-теориялық стилін дамыту үшін сыртқы тірек ретінде соларды кеңінен қолдануды білдіреді».
Бұдан оқушыларды нақты процестерді құру әдістемесімен оқыту математика курсының және ең алдымен дифференциалдық теңдеулердің негізгі шарттарының бірі.
Дифференциалдық теңдеулердің қолданбалы бағыты арқылы біз оқыту процесіндегі шынайы пән аралық байланысты орнатамыз [5] .
Жалпы математиканы оқыту әдістемесінің түрлері бағыттарында: оқыту процесін жақсарту, оқу пәндеріне қызығу бағытында жүргізіледі. Мазмұны жақын пәндердің өзара байланысы, тек оқушылардың білімдерінің сапасын арттырып қана қоймай, алынған білімдерді іс-тәжірибеде пайдалану дайындығына ықпал етеді, оқушылардың ғылыми дүниетанымын дамытады.
Соңғы жылдары зерттеушілердің пәнаралық байланысты ортануға қызығушылықтары да арта түсті. Біз пән аралық байланысты мәселені тұжырымдау сандары да арта түсті. Біз пән аралық байланысты жүйеліліктің көрінуі, табиғи құбылыстардың объективті өзара байланысының бейнесі ретінде қарастыруды дұрыс көрдік.
Пәнаралық байланыстар, оқытудың барлық қызметтерінің, атап айтқанда, білімділіктің, дамытушылық және тәрбиелік мәнінің орындалуына ықпал етеді. Бұл қызметтері өзара байланыста орындалады және бір бірін толықтырады.
Жоғарыда айтылғандардың бәрін жалпылап, дифференциалдық теңдеулердің гуманитарлық құраушысының негізгі бағыттарын тұжырымдауға тырысып көрейік.
Ең алдымен, бұл дифференциалдық теңдеулердің оқушыға қоршаған орта туралы дұрыс түсінікті қалыптастырудағы мүмкіндік беретін дүниетанымдылық, метадологиялық аспекті. Белгілі шамада бұған тақырыптың тарихи-математикалық, бөлігі ықпал етеді. Әрі қарай, дифференциалдық теңдеудің математикалық модельдеу әдісімен және пәнралық байланысты орнату мәселесімен тікелей байланысты аспектілерді ерекшелеу керек.
Ең соңында, дифференциалдық теңдеулер - бұл табиғат сөйлейтін тіл. Математика курсының тілдік аспектісі соңғы кезде математиканы оқыту әдістемесі облысындағы зерттеушілерді күннен күнге қызықтырып отыр. Математикалық тілді меңгеру, қазіргі заманда, адамның жалпы мәдениетін құрайтыны туралы ой соңғы жылдары тіпті жоққа шығарылмайды. Болашақ студенттер бұл ойды түсінуі үшін дифференциалдық теңдеулердің алатын орнын белгілеулері керек.
- ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ОҚЫТУ ӘДІСТЕМЕСІ
2. 1 Дифференциалдық теңдеулер туралы жалпы түсінік
Физиканың негізгі заңдарының бірі Ньютонның екінші заңына сәйкес тұрақты m массасы бар, материалды нүктенің түзу сызықты қозғалысында қозғалысты тудырушы
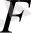 күші m масса мен
күші m масса мен
 үдеудің көбейтіндісіне тең, F=m*a. F күші өз кезегіңде x координатасына, оның v жылдамдығына және t уақыт моментіне тәуелді болуы мүмкін. Сондықтан F=m*a теңдігін былай қайта жазуға болады:
үдеудің көбейтіндісіне тең, F=m*a. F күші өз кезегіңде x координатасына, оның v жылдамдығына және t уақыт моментіне тәуелді болуы мүмкін. Сондықтан F=m*a теңдігін былай қайта жазуға болады:
(1)
Енді нүктенің жылдамдығы координатаның уақыт бойынша туындысына тең
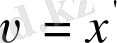 , ал үдеу - координатаның уақыт бойынша екінші туындысына тең
, ал үдеу - координатаның уақыт бойынша екінші туындысына тең
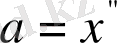 . Сондықтан теңдеу (1) келесіні білдіреді.
. Сондықтан теңдеу (1) келесіні білдіреді.
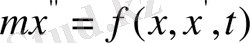 (2)
(2)
Біз (қозғалыс заңы) аргументі
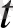 -ға тәуелді белгісіз x функциясымен оның бірінші және екінші ретті туышдысы және t аргументінің өзі енетін теңдеуді алдық. Бұл теңдеуді шешіп, біз нүктеге әсер етуші күштер бойынша нүктенің қозғалу заңын біле аламыз. Осындай және бұдан күрделірек теңдеуге машинаның, ракетаның, планета және т. б. бөліктердің қозғалу заңын келтіруге болады. Осындай теңдеулерді дифференциал теңдеулер деп атайды.
-ға тәуелді белгісіз x функциясымен оның бірінші және екінші ретті туышдысы және t аргументінің өзі енетін теңдеуді алдық. Бұл теңдеуді шешіп, біз нүктеге әсер етуші күштер бойынша нүктенің қозғалу заңын біле аламыз. Осындай және бұдан күрделірек теңдеуге машинаның, ракетаның, планета және т. б. бөліктердің қозғалу заңын келтіруге болады. Осындай теңдеулерді дифференциал теңдеулер деп атайды.
Анықтама 1 Дифференциалдық теңдеу деп ізделінді функцияның қандай да бір туындысымен қатар, осы функцияның өзін және оның дифференциалын біріктіретін теңдеулерді айттамыз.
Дифференциалдық теңдеулерге мыналар мысал бола алады:
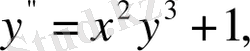
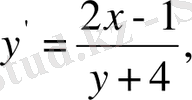
және т. б.
Соңғы теңдеулерде ізделінуші функция у және оның бірінші
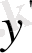 және
және
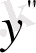 туындылары бар. Ал тәуелсіз айнымалы ретінде х еніп тұр.
туындылары бар. Ал тәуелсіз айнымалы ретінде х еніп тұр.
Мысал 1. Космостан жерге түсіп келе жатқан материалдық нүктенің қозғалысының дифференциалдық теңдеуін жазыңыз.
Шешуі. Бүкіл әлемдік тартылыс заңы бойынша нүктеге
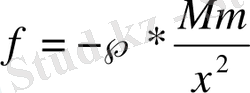 күші әсер етеді, мұндағы М - жердің массасы, m - нүктенің массасы
күші әсер етеді, мұндағы М - жердің массасы, m - нүктенің массасы
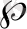 - пропорционалдық коэффициенті және х-нүктеден жердің бетіне дейінгі арақашықтық («минус» таңбасы қойылғанының себебі күштің бағыты координаттар осінің бағытана қарама-қарсы) . Ньютонның екінші заңы бойынша
- пропорционалдық коэффициенті және х-нүктеден жердің бетіне дейінгі арақашықтық («минус» таңбасы қойылғанының себебі күштің бағыты координаттар осінің бағытана қарама-қарсы) . Ньютонның екінші заңы бойынша
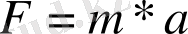 болғандықтан,
болғандықтан,
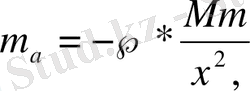 немесе
немесе
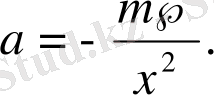 Бірақ
Бірақ
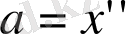 болғандықтан ізделінді дифференциалдық теңдеу
болғандықтан ізделінді дифференциалдық теңдеу
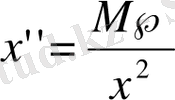
түрінде жызылады [6] .
Символдық түрде дифференциалдық теңдеу былай жазылады.
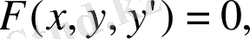
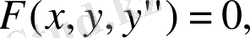
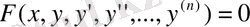
Жалпы алғанда, егер ізделінді функция бір белгісіз айнымалыға тәуелді болса, онда дифференциалдық теңдеу қарапайым дифференциалдық теңдеу деп аталады.
Көрсеткіштік өсудің және көрсеткіштік кемудің дифференциалдық теңдеуі физикалық, техникалық, биологиялық және әлеуметтік ғылымдардың көптеген есептерінің мынадай дифференциалдық теңдеуді.
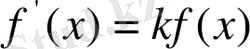 (3)
(3)
қанағаттандыратындай функцияларды табуда келтіріледі, мұндағы k - қандай да бір константа.
Көрсеткіштік функцияның формуласын біле отырып, мына теңдеудің
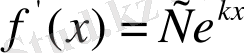 (4)
(4)
шешімі кез келген функция болатынын байқау қиын емес, мұндағы С-тұрақты. Ал С еркімізше алынатындықтан, дифференциалдық теңдеудің шешімдері шектеусіз көп болады.
(3) теңдеудің (4) түрдегі функциялардан өзге, басқа шешімдерінің болмайтынын дәлелдейік. Ол үшін (4) теңдеуді қанағаттандыратын кез келген f функциясын және
(5)
көмекші функциясын қарастырамыз. g функцияның туындысын табамыз:
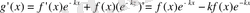
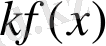 - тің орнына (3) теңдеудегі
- тің орнына (3) теңдеудегі
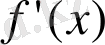 -ті қойып, мынаны шығарып аламыз:
-ті қойып, мынаны шығарып аламыз:
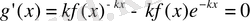
g функцияның туындысы нөлге тең болғандықтан, барлық х үшін
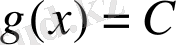 болады. (4) - тен мынау шығады:
болады. (4) - тен мынау шығады:
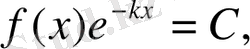 бұдан
бұдан
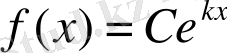
дәлелдемекшіміз де осы болатын.
Ескерту: Жоғарыда келтірілген талқылауларда біз f фунциясын бүкіл сандық түзуде анықталған және (3) теңдеуді қанағаттандырады деп ұйғарған болатынбыз. Нақтылы есептерде (3) теңдеуді тек қандай да бір аралықта ғана қанағаттандыратын функцияларды қарастыруға тура келеді. Әрине, ондай жағдайда (4) формуладан жалпы шешімді (3) теңдеу орындалатындай аралықта ғана табатынымыз түсінікті. (3) дифференциалдық теңдеудің мағынасы мынау - функцияның х нүктесіндегі өзгеру жылдамдығы сол функцияның осы нүктедегі мәніне пропорционал. Бұл теңдеу практикалық есептерді шешкенде жиі кездеседі.
Мысал 2. (Радиоактивтік ыдырау) . Айталық, бастапқы уақыт мезетінде радиоактивті заттың массасы мынадай болсын:
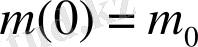
Ал уақыт өтуімен заттың m (t) массасының кему жылдамдығы оның мөлшеріне пропоционал болатыны белгілі, яғни мына теңдеу орындалады:
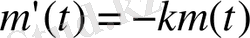
мұндағы k > 0. Жоғарыда тағайындалған қасиет бойынша
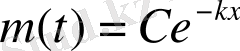 (6)
(6)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz