Ақпараттық-коммуникациялық технологияларды қолдана отырып мектепте арифметикалық және геометриялық прогрессияларды оқыту әдістемесі


Мазмұны
Кіріспе . . . 3
1 Математикада ақпараттық-коммуникациялық технологияны қолдану туралы теориялық білім
1. 1 Математиканы оқыту процесінде ақпараттық-коммуникациялық технологияларды (АКТ) қолдану . . . 5
1. 2 МАТЕМАТИКА МЕКТЕБІНІҢ КУРСЫНДА ІЛІКТІЛІКТІ ЗЕРТТЕУДІҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ . . . 45
2. АКТ-ны қолдана отырып, мектептегі математика курсында сандық тізбектерді оқытудың әдістемелік тәсілі . . . 46
2. 1 АКТ көмегімен арифметикалық прогрессияны зерттеу . . . 46
ЖОСПАР - САБАҚТЫҢ НӘТИЖЕСІ
2. 2 Ақпараттық-коммуникациялық технологияларды қолдана отырып, кіші мектеп оқушыларының геометриялық көріністерін қалыптастыру . . . 56
ҚОРЫТЫНДЫ . . . 68
Әдебиеттер тізімі . . . 71
КІРІСПЕ
«Сандар тізбегі» тақырыбы ежелгі дәуірде пайда болды және математика ғылымының дамуына үлес қосқан ғалымдардың есімдерімен байланысты әр түрлі тізбектерді зерттейді. Сандар тізбегіне байланысты көптеген мәселелер ежелгі уақытта пайда болған. «Сандар тізбегі» тақырыбы негізгі мектеп бағдарламасына енгізілген және базалық деңгейде, ең бастысы қарапайым сандық тізбектер - арифметикалық және геометриялық прогрессияны зерттеуге бағытталған. Алайда, нақты өмірде біз әртүрлі типтермен жиі кездесеміз тізбектер. Олардың көпшілігі әртүрлі ғылымдарда қолданылады. Мысалы, Фибоначчи сандары ежелгі тарихты хронологияда және кезеңдеуде, сәулет өнерінде, музыкада, биологияда, астрономияда, бағаны болжауда қолданылады, грек вазалары мен спираль тәрізді галактикалардың пішінін, күнбағыс пен ұлу үйінің құрылымын анықтайды. Н. Слоанның бүтін тізбектер туралы анықтамалық кітабында 2300 бүтін тізбектер жинақталған және тапсырыс берілген, бұл олардың қолдану аясы өте кең екендігін білдіреді.
Орта мектеп алгебра курсында «Арифметика және геометриялық прогрессиялар» тақырыбы бөлек оқылады, тек тоғызыншы сыныпта, мектеп бағдарламасының басқа бөлімдерімен аз ортақтықтары бар. Бірақ, бұған қарамастан, тек n-ші мүшенің формулаларын және бірінші n мүшесінің қосындыларын ғана емес, сонымен қатар арифметикалық және геометриялық прогрессиялардың қасиеттерін білу қажет есептер ҰБТ-да және жоғары оқу орнына түсу емтихандарында. Студенттің білімі жеткілікті жоғары деңгейде болуы үшін прогрессияны зерттеу кезінде оның танымдық белсенділігін белсендіру қажет. Геометриялық және арифметикалық прогрессиялар мектептің алгебра курсында ғана емес өмірде қолданыста маңызды рөл атқарады.
Өмірде қолдану аясы өте кең. Мысалы, химияда арифметикалық прогрессияда температура көтерілген сайын, химиялық реакциялардың жылдамдығы геометриялық прогрессияда өседі. Әдебиетте: « . . . Ол хореядан иамба бола алмады, өйткені біз ажырату үшін күрескен жоқпыз . . . ». Ямбия мен хореяның айырмашылығы өлеңнің екпінді буындарының әр түрлі орналасуында. Iambic - бұл 2, 4, 6, 8, жұп буындарына баса назар аударатын поэтикалық метр . . . Стресті буындардың сандары арифметикалық прогрессияны 2-ші мүшемен және 2-ші прогрессиямен айырмашылықты құрайды. Хорея - бұл поэтикалық метр өлеңнің тақ буындарына екпін беру. Стресті буындардың сандары арифметикалық прогрессияны құрайды 1, 3, 5, 7, . . . және т. б. ҰБТ тапсырмаларында математикадан сонымен қатар арифметикалық және геометриялық прогрессияларды қолдануға арналған, бірақ практикалық мазмұны бар тапсырмалар бар. Сондықтан, студент мектеп курсынан өзіне белгілі материалды қайталап, тіпті көптеген жаңа және қызықты нәрселерді білуі үшін бұл курстың толық сипаттамасын беру өте маңызды. Бұл қорытынды біліктілік жұмысы тақырыбының өзектілігі.
Зерттеу нысаны - тақырыпты ұсыну процесі.
Ақпараттық-коммуникациялық технологияларды қолдана отырып, мектептегі математика курс да «дәйектілік».
Нәрсе зерттеу: Мүмкіндіктер зерттеу арифметикалық ақпараттық-коммуникациялық технологиялар арқылы геометриялық прогрессия.
Қашан орындау жұмыс болды қолданылған келесісі зерттеу әдістері:
1. Таңдалған тақырыптың теориялық негіздерін зерттеу;
2. Талдау мектеп оқулықтары және материалдар ҰБТ осы тақырып бойынша «Арифметикалық және геометриялық прогрессиялар»;
3. Зерттеу тақырыбы бойынша тест тапсырмаларын өздігінен таңдау;
4. Дамуы әдістемелік ұсыныстар арқылы ақпараттық-коммуникациялық технологияларды қолданатын тақырып «Арифметикалық және геометриялық прогрессиялар».
Қорытынды біліктілік жұмысын аяқтау барысында оның құрылымы анықталды: мазмұны, теориялық және практикалық бөлігі, қорытынды, пайдаланылған әдебиеттер тізімі.
Кіріспеде өзектілік негізделеді, қорытынды жұмыстың мақсаты мен міндеттері қойылады, оларды шешу әдістері келтірілген.
Бірінші тарауда тақырып бойынша барлық теориялық материалдар бар
«Арифметикалық және геометриялық прогрессиялар». Негізгі ұғымдардың анықтамалары берілген, прогрессия мүшелерінің қасиеттері, арифметикалық және геометриялық прогрессияның алғашқы n-мүшелерінің қосындысы қарастырылған. Зерттеу тақырыбын ұсыну бойынша мектеп оқулықтарына талдау жасалды.
Екінші тарауда тақырып бойынша зерттеудің практикалық бағыты келтірілген.
Қорытындысында атқарылған жұмыстардың нәтижелері келтірілді.
1 Математикада ақпараттық-коммуникациялық технологияны қолдану туралы теориялық білім
1. 1 Математиканы оқыту процесінде ақпараттық-коммуникациялық технологияларды (АКТ) қолдану
Математиканы оқыту процесінде ақпараттық-коммуникациялық технологияларды (АКТ) пайдалану білім беру саласының ажырамас бөлігі болып табылады. Бұл факт оқу процесін оңтайландыруға, білім беру үдерісінің қанықтығын арттыруға мүмкіндік береді.
Жалпы базалық білім негізінде колледжге түсетін студенттер бір жылдық оқу жылы мектепте екі жыл оқыған болатын бағдарламаны аяқтауы керек. Олар оқу материалын игеруде қиындықтарға тап болады, жаңа білімді бекіту үшін оқу уақытының жетіспейтіндігін сезінеді, бұл олардың танымдық белсенділігінің төмендеуіне әкеледі.
Компьютерлік технологияларды білім беруде қолдану сөзсіз, өйткені оқытудың тиімділігі мен қалыптасып жатқан білім мен дағдылардың сапасы едәуір артады. Математика сабағында компьютерлік бағдарламалық жасақтаманы қолдану дәстүрлі білім беру түрлерін әртараптандырып қана қоймай, сонымен қатар әр түрлі мәселелерді шешуге, соның ішінде оқу пәніне қызығушылықты арттыруға, оқушылардың танымдық белсенділігіне, білім деңгейін көтеруге мүмкіндік береді. . Күтілетін нәтижеге жету үшін білім беру процесінде АКТ үнемі қолданылуы керек. Мұғалім компьютерде еркін сөйлеуі керек, оқушыны жетілдіруге бағытталған әр түрлі оқу іс-әрекетінде оқу-әдістемелік кешенді (ОӘК) қолданудың икемді әдісін қолдануы керек. Ақпараттық технологияларды қолдана отырып сабақ өткізу - оқудағы күшті стимул. Осындай сабақтар арқылы оқушылардың психикалық процестері белсендіріледі: қабылдау, зейін, есте сақтау, ойлау; танымдық қызығушылық толқуы әлдеқайда белсенді және жылдамырақ. Барлық мұғалімдердің мақсаты - оқытудың тиімділігі мен оқушылардың пайда болатын білімдері мен дағдыларының сапасын арттыру. Бұл мақсатқа ақпараттық-коммуникациялық технологияларды білім беру үдерісіне енгізу арқылы қол жеткізуге болады.
Осы мәселені зерттеу үшін мен келесі міндеттерді атап өттім:
- математика бойынша оқу бағдарламасын талдау және оқу пәнін оқытудың әртүрлі кезеңдерінде ақпараттық-коммуникациялық технологияларды қолдану мүмкіндігін анықтау;
- математика сабағында қолданылатын компьютерлік бағдарламалық жасақтаманы оқып үйрену;
- оқу үдерісінде интерактивті тақтаның мүмкіндіктерін жүйелі түрде пайдалану және АКТ-ны оқу сабағының әртүрлі кезеңдерінде қолдану;
- АКТ-ны қолдану нысандары мен мақсаттарын зерттеу;
- АКТ-ны оқу сабағының әр түрлі кезеңдерінде қолдану нұсқаларын қарастыру.
Математика студенттерден тұрақты, ұқыпты және маңызды өзіндік жұмысты талап ететін ең ауыр оқу пәндерінің бірі болып табылады. Әр оқу жылының басында мен оқушылардың математикамен байланысы туралы сауалнама жүргіземін, нәтижесінде көптеген оқушылардың пәнге деген теріс көзқарасы бар екенін байқауға болады, геометрия әсіресе қиын.

Математика сабағында сыныптағы ақыл-ой жүктемесінің жоғарылауы мені оқушылардың бүкіл оқу сабағында қызығушылығын, оқылатын пәнге деген қызығушылығын қалай сақтау керектігі туралы ойлады. Математикаға деген қызығушылықты сақтау және оқу процесін сапалы өткізу үшін мен өз сабағымда ақпараттық технологияларды белсенді қолданамын.
Ақпараттық-коммуникациялық технологиялар дегеніміз - компьютерлік құрылғылардың, сондай-ақ көмегімен жүзеге асырылатын ақпаратпен өзара әрекеттесу процестері мен әдістері. АКТ-ның білім беру құралдары белгілі бір педагогикалық мәселелерді шешуге арналған, пәндік мазмұны бар және студенттермен өзара әрекеттесуге бағытталған әр түрлі бағдарламалық және аппараттық құралдарды қамтиды.
Математика сабақтарын дайындау мен өткізуде әртүрлі бағдарламалық өнімдер мен интернет-ресурстар пайдаланылады:
- бейне оқулықтар, бейнеклиптер;
- модульдер, флеш-бейнелер;
- мультимедиялық презентациялар банкі;
- электрондық оқулықтар;
- дамыған қашықтықтан оқыту курсының материалдары;
- тестілер, тренажерлер, оның ішінде онлайн және т. б.
Оған бейімделген қосымша технологияларды (бағдарламалық өнімдер, Интернет, желілік және демонстрациялық жабдықтар) пайдаланатын компьютердің мүмкіндіктері ақпараттық-коммуникациялық технологиялардың материалдық базасын құрайды.
АКТ-ны қолдану оқыту үдерісін студенттер үшін айқын, ұмытылмас, ақпараттандыратын, пайдалы және іс жүзінде мағыналы ету үшін ең бай мүмкіндіктерді ұсынады. Дидактикалық мүмкіндіктер таусылмайды, өйткені олар оқу материалын ұсынудың әр түрлі тәсілдерін біріктіруге, оқыту, дамыту және тәрбиелеу мақсаттарын жүзеге асыруға бағыттауға мүмкіндік береді.
Математика - бұл АКТ-ны қолдану оқу іс-әрекетінің барлық түрлерін күшейтуге болатын пәндердің бірі: жаңа материалды меңгеру, үй тапсырмасын дайындау және тексеру, өзіндік жұмыс, бақылау және бақылау жұмысы, сыныптан тыс жұмыс, шығармашылық жұмыс. АКТ-ны қолдану арқылы көптеген әдістемелік мақсаттарды тиімді жүзеге асыруға болады.
АКТ-ны белгілі тақырыптарды, бөлімдерді оқуда, белгілі дидактикалық мәселелерді шешуде қолдануға болады. Мысалы, «Тригонометрия» тақырыбы бойынша үй тапсырмасын Stratum2000 бағдарламасын пайдаланып тексеруге болады.
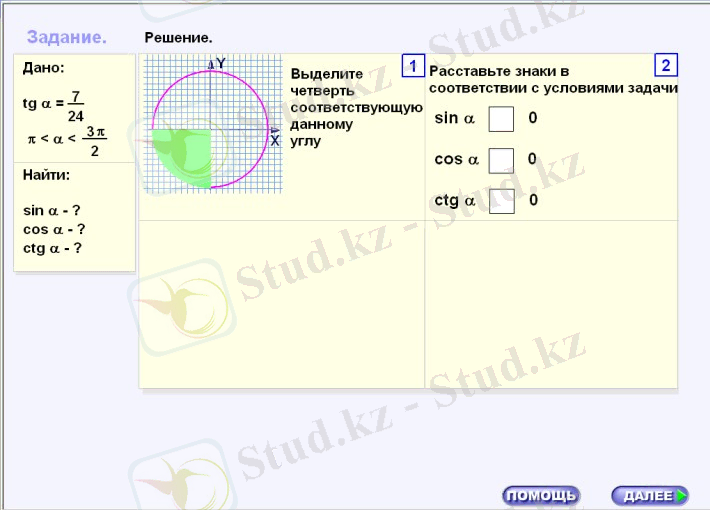
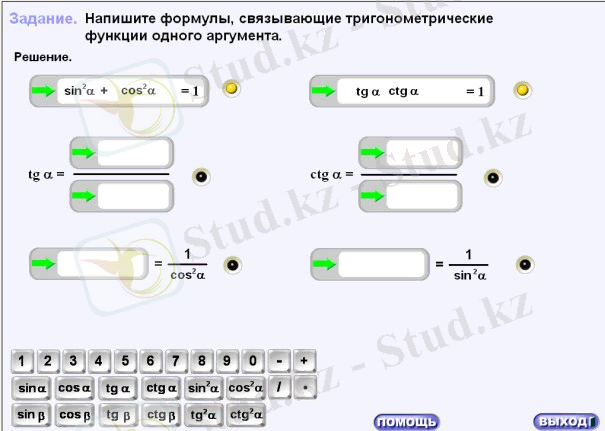
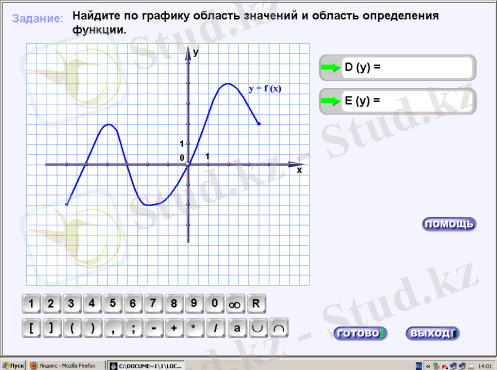
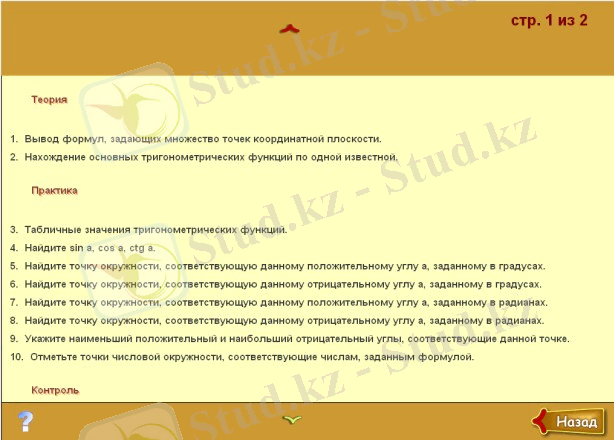
Stratum 2000 ортасының визуалды жобалау құралдары ақпараттық сілтемелермен байланысқан объектілерден жүйенің прототипін құруды қамтамасыз етеді. Оларды бейнелеу үшін статикалық және анимациялық графика қолданылады. Объектілердің әрекеті қарапайым математикалық тілде сипатталады. Математикалық функциялардың бай жиынтығы, сызықтық және сызықтық емес теңдеулер жүйесін шешуге арналған құралдар бар. Нысандар иерархияға ие бола алады және кітапханаларда сақталады. Құрылғаннан кейін объектілерді басқа жүйелерде дербес пайдалануға болады. Мұның бәрі пайдаланушыға жүйені ресми түрде ұсынудың ыңғайлы тәсілін таңдауға мүмкіндік береді.
Математиканы оқыту процесінде ақпараттық технологияны әр түрлі формада қолдануға болады:
- тренингтердің мультимедиялық сценарийлері (презентациялар) ;
- оқыту және демонстрациялық бағдарламалар;
- интерактивті тақтамен жұмыс;
- жобалық қызмет;
- ғылыми-зерттеу қызметі;
- сыныптан тыс жұмыстар.
АКТ-ны қолданудың артықшылықтарының бірі - өздік жұмыс уақытының күрт артуы. Мультимедияны сабақта қолдану көптеген принциптерді жүзеге асырады:
- көріну принципі. Кез-келген білім беру сабағында иллюстрациялық материалды, аудиоматериалды, сирек иллюстрация қорларын пайдалануға мүмкіндік береді. Материалдың анықтығы оны студенттерде игеруді күшейтеді, өйткені студенттер қабылдаудың барлық арналары - визуалды, механикалық, есту және эмоционалды;
- күш принципі. Сабақ барысында презентацияларды пайдалану бірнеше рет оқылған немесе оқылған материалға оралуға мүмкіндік береді. Оқу бағдарламаларын қолдану алдыңғы сабақтардың материалын бір сабақта қайталауға және бекітуге мүмкіндік береді. Оқу материалы үлкен көлемде және берік жатталады;
- қол жетімділік принципі. Білім беру және дамытушы бағдарламалар оқытудың сараланған әдісін жүзеге асырады, студенттерді жаттауға емес, оқу материалын түсінуге бағыттайды. Тапсырмалар жеңілден қиынға қарай беріледі;
- жүйелілік принципі. Презентация сабақтарын пайдалану жаңа тақырыптарды түсіндіру үшін алдыңғы сабақтардың элементтерін көрсетумен қатар, бір тақырып бойынша сабақтар жүйесін дамытуға мүмкіндік береді.
Мультимедиялық сценарийлер жаңа материал ұсыну кезінде де, өтілгенді қайталау кезінде де қолданылады. Презентацияларды PowerPoint ортасында ғана емес, сонымен қатар SMART Notebook бағдарламалық жасақтамасының көмегімен де жасауға болады.
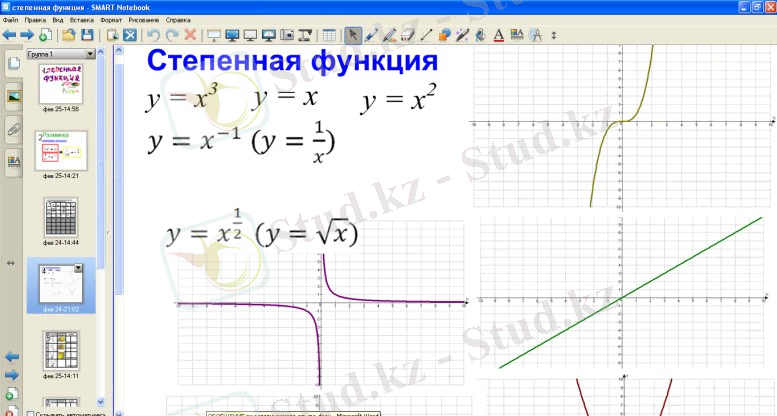

SMART Notebook бағдарламалық жасақтамасы сабақ немесе презентация жасау үшін қолданылады. . Notebook файлдарының әрқайсысы жеке объектілері, қасиеттері мен параметрлері бар беттер жиынтығынан тұрады. Сіз өзіңіздің парағыңызға қолмен объектілерді, геометриялық фигураларды, түзу сызықтарды, мәтіндерді, сызбаларды, Adobe® Flash® Player үйлесімді мазмұнын және кестелерді қоса аласыз. Бұл объектілерді кез-келген уақытта басқаруға және олардың түрін өзгертуге болады. SMART Notebook бағдарламалық жасақтамасы жаңа интерактивті анимациялық сабақтар құруға, және бұрын құрылған барлық оқу материалдарын Word, Excel, PowerPoint сияқты барлық жалпы бағдарламаларға біріктіруге, осы ортаның кез келген көздерінен бар сандық білім беру ресурстарын қосуға мүмкіндік береді: Интернет, флэш анимациялар мен бейне файлдар.
Оқушылар үлкен ынтамен интерактивті тақтамен жұмыс істейді, ол материалға түсініктеме беруге, бөлектеуге, нақтылауға, электрондық маркерлерді қолданып қосымша ақпарат қосуға мүмкіндік береді.
Ақпараттық-коммуникациялық технологиялардың дамуына байланысты электронды оқыту құралдары кеңінен қолданыла бастады - компьютерлік ақпараттық технологияларды қолданып жасалған оқу құралдары. Функционалды мақсаты бойынша электрондық оқыту құралдарын келесі түрлерге бөлуге болады:
- ақпараттық-иллюстрациялық және ақпараттық-анықтамалық (кәдімгі көрнекі құралдарды ауыстырыңыз, қажетті ақпаратты таңдау және бейнелеу мүмкіндігін қамтамасыз етіңіз; олардың әдіснамалық мақсаты - ақпаратты жүйелеу дағдылары мен дағдыларын қалыптастыру) ;
- дамытушы бағдарламалар, тренажерлар (оқушылардың есте сақтау қабілетін, зейінін, логикасын, кеңістіктік ойлауын дамытуға бағытталған,
бұрын өткен материалды қайталау немесе бекіту кезінде қолданылады) ;
- оқыту бағдарламалары (оқу материалын меңгерудің дәйектілігі мен қарқынын, жаттығулардың кезектілігін анықтайды, жауаптардың дұрыстығын растайды немесе экранда жіберілген қателіктердің түсіндірмесін көрсетеді) ;
- бақылау бағдарламалары (зерттелген материалды игеру дәрежесін бақылау және бағалау; мұндай бағдарламаларға әр оқушының жеке сауалнамасы кіреді) .
Сонымен, функционалдық мақсатына байланысты бір жаттығу сабағында бірнеше бағдарламаны қолдануға болады.
Мысалы, «Функциялар», «Экспоненциалды және логарифмдік функция», «Тригонометриялық функция» тақырыптарын оқығанда «Әмбебап білім беру плоттері» ОЖСЖ-н қолданған жөн.
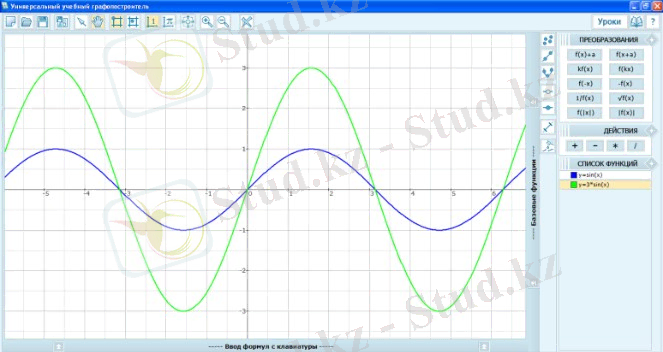
«Әмбебап білім беру плоттері» ОЖСБ-ны педагогикалық қызметтің әр түрлі кезеңдерінде қолдануға болады: білім беру сабағына дайындық, жаңа материалды фронтальды түсіндіру, жеке танымдық іс-әрекетті ұйымдастыру, оқу материалын бекіту және қайталау, оқу нәтижелерін бақылау қабілетімен әр оқушының нәтижесін қадағалау. Оның көмегімен студенттің мүмкіндігі бар: мектеп математикасы курсында берілген барлық негізгі функциялардың графиктерін құруға; теңдеулер, теңсіздіктер, теңдеулер мен теңсіздіктер жүйелерін графикалық түрде шешу; функция графиктерін түрлендіру (кішірейту, созылу, жылжу және т. б. ) .
Білімді бақылауды VeralTest бағдарламасының көмегімен жүзеге асыруға болады. Бұл оқушылардың білім деңгейін тест тапсырғаннан кейін бірден бағалауға мүмкіндік береді.
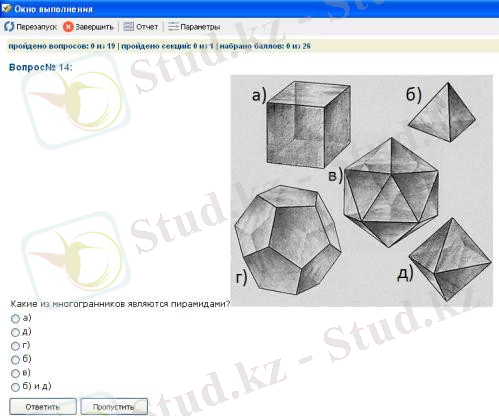
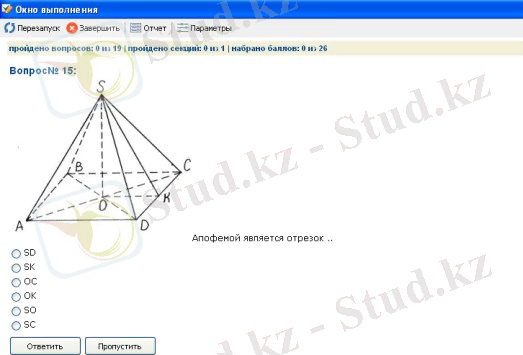
Математика сабағында АКТ-ны қолдану жұмыстың анықтығы мен жылдамдығына байланысты материалды оқу уақытын қысқартуға, оқушылардың білімін интерактивті режимде тексеруге мүмкіндік береді, бұл оқытудың тиімділігін арттырады. Осы мақсатта геометрия сабағында мен «Тірі математика» және «Тірі геометрия» оқу-әдістемелік жинақтарын жиі қолданамын.
«Тірі математика» ОӘК бағдарламаларға жатадыдинамикалық геометрия немесе «интерактивті геометриялық жүйелер», оны виртуалды математикалық зертхана деп те атайды. «Тікелей эфир
математика »теоремаларды келесі дәлелдеу үшін тұжырымдауға, сонымен бірге дәлелденген теоремаларды растауға және олардың түсінігін дамытуға көмектеседі, оқушының бақыланатын геометриялық құбылыстардағы заңдылықтарды ашуға мүмкіндік береді, кеңістіктегі қиялын дамытады. «Тірі математика» бағдарламасының көмегімен дене пішіні ұғымдары, сондай-ақ күрделі жүйелердің динамикалық иллюстрациясы туралы алғашқы түсінік алуға көмектесетін интерактивті математикалық модельдер құруға болады. Бұл бағдарламалар түрлі-түсті суреттер жасауға, оларды «жандандыруға», сондай-ақ геометриялық мәндерді өлшеуге мүмкіндік береді. Оқу-әдістемелік жинақ Key Curriculum Press-тің қуатты геометриялық Sketchpad бағдарламалық жасақтамасына негізделген. Ол жаңа технологиялар институтының әзірлемелерімен толықтырылды - компьютерлік альбомдар, проблемалық кітаптар, бағдарламаны пайдалану мысалдары,
АКТ-ны қолдану дербес білім беру және ғылыми-зерттеу жұмыстарына (модельдеу, жоба әдісі, презентацияларды, басылымдарды әзірлеу және т. б. ) мүмкіндік береді, сол арқылы студенттердің шығармашылық белсенділігін дамытады.
Ақпараттық технологияларды, менің ойымша, математика сабағының әр түрлі кезеңдерінде жүзеге асыруға болады:
- ауызша жаттығулар жасау кезінде, тапсырмаларды жедел түрде ұсынуға және оларды орындау нәтижелерін түзетуге мүмкіндік береді;
- фронтальды тәуелсіз және үй жұмысын тексеру кезінде
нәтижелердің визуалды бақылауын қамтамасыз етеді;
- білім беру мәселелерін шешкен кездесызбаны аяқтауға, шешім жоспарын құруға және осы жоспар бойынша өзіндік жұмыстың аралық және соңғы нәтижелерін бақылауға көмектеседі;
- жаңа материалды игеру кезіндеоқу материалын әр түрлі көрнекі құралдармен безендіруге мүмкіндік береді. Қолдану әсіресе процестің даму динамикасын көрсету қажет болған жағдайда тиімді. Тақырыптар бойынша жаңа материалды түсіндіру кезінде сыныпта
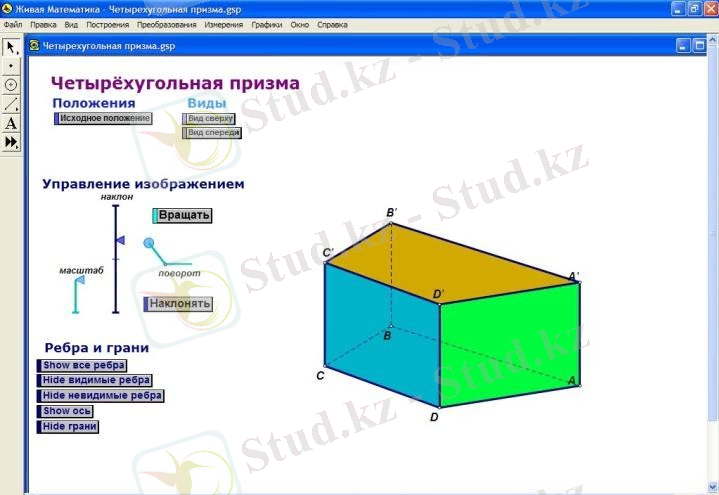
«Стереометрияға кіріспе», «Түзулер мен жазықтықтардың параллелдігі және перпендикулярлығы» Мен ESO қолданамын »Математика. Стереометрия «тақырыбына арналған.
Электрондық оқыту құралы білім беру мекемелеріне арналған математика бағдарламасына сәйкес 10-сыныпта оқытылатын стереометрия курсын оқытуда компьютерлік қолдау көрсетуге арналған. Оқу материалдары теориялық және иллюстрациялық анықтамалық материалдардан (суреттер, анимациялар, компьютерлік модельдер, 3D нысандар) және қалыптасады
құрылымдалған арқылы тақырыптар: «Кіріспе жылы стереометрия «Түзулер мен жазықтықтардың параллельдігі», «Түзу мен жазықтықтың перпендикулярлығы. Жазықтықтардың перпендикулярлығы »тақырыбында өтті.
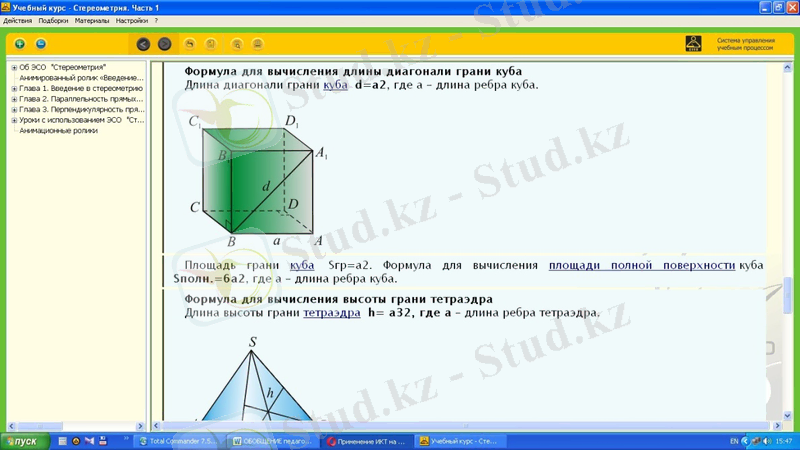
Бұл ESS тек білімді игеру жүйесін ғана емес, сонымен бірге шешімнің жалпы схемасын және шешімнің нақты мысалын бейнелейтін анимациялық клиптер түрінде құрастыруға арналған негізгі міндеттерді де қамтиды; есептеу немесе дәлелдеу үшін анықтамалық тапсырмалар, оқушылардың ақыл-ой әрекетін басшылыққа алатын қадамдық нұсқаулары бар тапсырмалар түрінде; есептер шығарудың мысалдары (анимациялық бейнелер есептер шығаруды иллюстрациялайды) ; білім беру міндеттері (шешуге арналған қадамдық нұсқаулықтан тұратын тапсырмалар) ; көп деңгейлі тапсырмаларды тексеру.
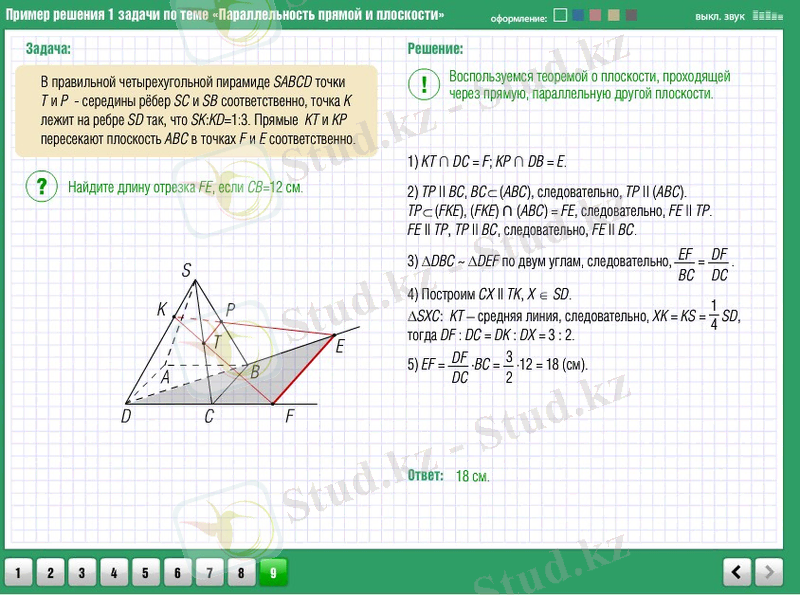
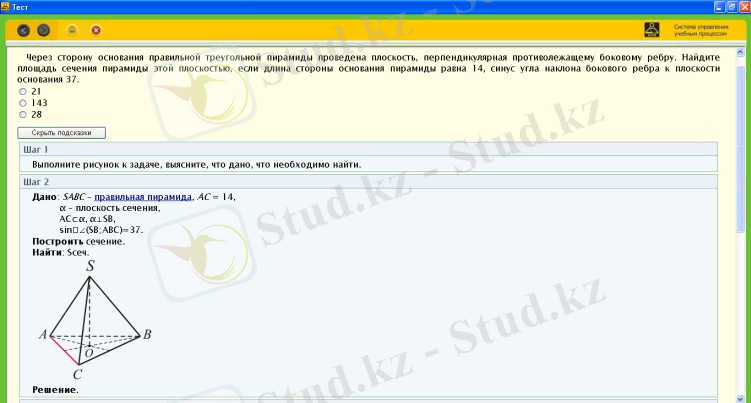
Әзірленген интерактивті тапсырмаларды қолдану тиімділігін бағалай отырып, олардың жүйелік қолданылуы оқу материалын меңгерудің тұтастығы мен жүйелілігін қамтамасыз ететіндігін, студенттерге тәуелсіздік танытуға мүмкіндік беретіндігін, ынтасын арттыруға және өзін-өзі басқару үшін оңтайлы жағдайлар жасауға мүмкіндік беретіндігін атап өткен жөн. бақылау.
Ойлаудың көрнекі-бейнелі компоненттері адам өмірінде өте маңызды рөл атқаратындықтан, оларды АКТ-ны қолдана отырып, материалды оқуда қолдану оқытудың тиімділігін арттырады:
- графика және анимация оқушыларға күрделі логикалық математикалық конструкцияларды түсінуге көмектеседі;
- студенттерге интерактивті тақтаның экранындағы әртүрлі объектілерді манипуляциялауға (зерттеуге), олардың қозғалу жылдамдығын, көлемін, түсін және басқаларын өзгертуге берілген мүмкіндіктер оқу материалын сезімдерді толық қолдана отырып игеруге мүмкіндік береді.
Нәтижесінде студенттердің ынтасы артады, олардың танымдық белсенділігі белсендіріледі және нәтижесінде оқу пәні бойынша білім сапасының деңгейі артады.
Интерактивті тапсырмаларды қолдана отырып, оқу сабақтарын талдау оқу процесінде электронды оқу құралдарын пайдалану ауызша есептеу дағдыларын жетілдірудің оңтайлы жағдайларын жасауға ықпал ететіндігін, жаңашылдықтың, сананың, белсенділіктің, көрнекілік пен қол жетімділіктің дидактикалық принциптеріне сәйкес келетіндігін, жұмыстың ұжымдық, жұптық және жеке түрлері.
АКТ-ны пайдалану шарттарын таңдау кезінде мен мыналарды ескеремін:
- зерттелген тақырыпқа сәйкес бағдарламалардың болуы, оқулықтағы материалдың ұсынылуымен сәйкестігі;
- компьютердегі жұмыс орындарының саны;
- оқушылардың компьютерді пайдаланып жұмыс істеуге дайындығы;
- оқушылардың үй жұмысын орындау кезінде немесе материалды өз бетімен оқып үйрену кезінде компьютерлік технологияны қолдану қабілеті.
АКТ-ны сабақтарда жүйелі түрде қолданудың нәтижесі мұғалімнің өзінің біліктілігін арттыру, оқушыларды белсенді іс-шараларға көптеп тарту, оқушылардың зейінін арттыру, олардың ынтасын арттыру, қиялын және қиялын дамыту, сонымен бірге тиімділігі болып табылады. сыныптың өзі өседі. Мұның бәрі оқу пәні туралы терең және берік білімнің кепілі ретінде қызмет етеді және студенттің жеке басының дамуын алдын-ала анықтайды.
Заманауи ақпараттық технологияларды пайдалану мыналарға ықпал етеді:
- оқу процесінің тиімділігі мен сапасын арттыру;
- танымдық іс-әрекеттің белсенділігін арттыру;
- көлемді ұлғайту және қажетті ақпаратты іздеуді оңтайландыру;
- ойлаудың әртүрлі түрлерін дамыту;
- коммуникативті дағдыларды дамыту;
- компьютерлік графиканы, мультимедиялық технологияны қолдану арқылы эстетикалық тәрбие беру;
- ақпараттық мәдениетті қалыптастыру, ақпаратты өңдеу мүмкіндігі;
- эксперименттік зерттеу қызметін жүзеге асыру дағдыларын қалыптастыру;
- ақпараттық сауатты адамды дайындау.
Бүгінгі күні АКТ-ны математика сабағында қолдану өзекті және қажет болып көрінеді. Білім берудің ақпараттық кеңістігінде мұғалімнің де, оқушылардың да АКТ құралдарын иемденуі балалардың ой-өрісін кеңейтуге, оқушылардың жеке ерекшеліктерін ашуға, оқу қызметін әртараптандыруға және материалды ұсынуға мүмкіндік береді. жан-жақты
Математика сабақтарында АКТ-ны қолдану мыналарды қамтамасыз ететіндігін тағы бір атап өткім келеді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz