Үшінші ретті туынды

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 24 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ
3
1ТУЫНДЫ ҰҒЫМЫН ЖӘНЕ ОНЫҢ ҚОЛДАНЫЛУЫН ОҚЫП
ҮЙРЕНУДЕ ТАРИХИ МӘЛІМЕТТЕРДІ ПАЙДАЛАНУ
5
0.1 Туынды ұғымын пайдалануда тарихи мағлұматтарды қолдану
5
0.2 Туындыға қолданылатын теоремалар
8
2. Жаңартылған білім беру бағдарламасы бойынша туындыны қолдануды оқыту әдісі
14

2.1 Жаңартылған білім беру мазмұны аясында оқытудың негіздері
14
2.2 Туынды оқыту әдістемесі
18
ҚОРЫТЫНДЫ
27
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР
28

КІРІСПЕ

Кез келген ғылымның негізін үйрену танымның нәтижелері жинақтаған ғылыми ұғымдар мен категориялардың жүйесін меңгеру болып табылады.
Педагогика ғылыми ұғымдарды олардың таным үрдісіндегі гнесеологиялық және психологиялық маңызына сүйене отырып, білім мазмұнының басты құрылымдық бірлігі ретінде анықтайды.
Ғылыми ұғымдарды саналы да, терең меңгергенде ғана оқушылардың қоршаған дүниені толық, бүтін қабылдауларына жағдай туғызуға болады, жан-жақты өз бетінше және белсенді ойлайтын адам етіп қалыптастыруға болады.
Дүние таным өкілдері ұғым-мидың, материяның жоғарғы жемісі деп атап көрсеткен. Әр ғылым саласы бойынша пайда болған ұғым өзінің даму кезеңдерінде өзгеріссіз қалып қоймайды. Заттар мен құбылыстардың жаңа қасиеттер мен белгілерге ие болуы нәтижесінде ұғым мазмұны қоюланып, молая түседі, көлемі кеңиді, олардың қатыстары мен байланыстары толығырақ айқындалады.
Жұмыстың өзектілігі: математика оқыту барысында оқушылардың қай тақырыпты меңгеруге қиналатындығын анықтаудың маңызы зор. Оқушы қандай да бір тақырыпты өз дәрежесіне меңгере алмаса, соның салдарынан келесі өтілетін материалды түсінбей қалуы мүмкін. Туынды тақырыбын меңгеру және оны басқа ғылымдармен байланысын көре алудың маңызы зор.
Жалпы туынды ұғымына мына түрде анықтама беріледі:
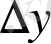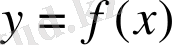өсімшесінің өсімшесіне қатынасының, осы нольге ұмтылғандағы, шегі берілген функциясының х нүктесіндегі туындысы деп аталады.
Курстың жұмыстың мазмұнын ашуға Исқақов, Көбесов, Колягин, Мишин және т.с.с. авторлардың еңбектері мен мақалалары қолданылды.
Жұмыстың зерттеу нысаны: туынды және оны оқып үйренуде тарихи мағлұматтарды қолдану әдістемесі.
Жұмыстың мақсаты:
* Оқыту процесінде оқушының санасына ғылыми теориялардың негізін қалаумен және оның туынды ұғымының қалыптастыру;
* Туынды және оның қолданылу әдістері мен идеяларын толық және терең түсінетін, оқушылардың қиындықтары әртүрлі есептерді шығару қабілеттерін дамытуға кепілдік беретін білімдер, іскерліктер мен дағдылардың жоғары деңгейіне қамтамасыз ету;
* Алынған білімдерді теориялық және тәжірибелік мәселелерді шешуге қолдана білу;
* Оқушыларды туынды және оның қолданылуын оқып үйренуде тарихи мағлұматтарды пайдалану, бұл ұғымды меңгеру арқылы ойлау қабілеттерін дамыту, тиімді жақтарын көре алу, пәнге деген қызығушылығын арттыру болып табылады.
Жұмыстың бағыттылығы: теориялық тарихи зерттеу арқылы.
Жұмыстың міндеті:
* Туынды ұғымын түсіну;
* Оны тәжірибеде қолдана білу;
* Тарихпен байланыстыра отырып түсіну;
* Оқушылардың туынды тақырыбын жетік меңгеруі.

1. туынды ұғымын оқып үйренуде тарихи мәліметтерді пайдалану
1.1. Туынды ұғымын пайдалануда тарихи мағлұматтарды қолдану
Туындылар және олардың функцияларды зерттеуде қолданылуы қарастырылатын математиканың бөлімі дифференциалдық есептеу деп аталады. Айырманы көрсететін 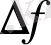түріндегі өсімше туындылармен жұмыс істегенде елеулі орын алады.
Туынды термині derivee деген француз сөзінің қазақша сөзбе-сөз аудармасы, оны 1797 ж. Жозеф Луи Лагранж (1736 - 1813) енгізген, қазіргі кездегі 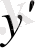, 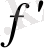белгілеулерін де сол енгізген-ді. Бұл атау мынадай ұғымның мағынасын ашады: 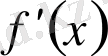функциясы 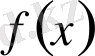-тен шығады, 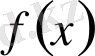-тің туындысы болып табылады. И. Ньютон функцияның туындысын флюксия деп, ал функцияның өзін флюента деп атаған. Г. Лейбниц дифференциалдық қатынас туралы айтқан және туындыны 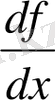түрінде белгілеген. Бұл белгілеу қазіргі әдебиетте де жиі кездеседі. Лейбниц 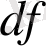символын 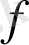функциясының дифференциалын белгілеу үшін таңдап алған. 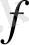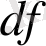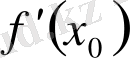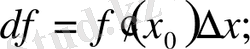функциясының дифференциалы - туындысының өсімшесіне көбейтіндісі,яғни белгілеуін 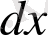-пен алмастырып, оны былай да жазуға болады: 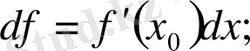осыдан .
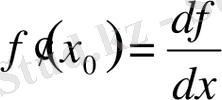Дифференциалдық есептеуді Ньютон мен Лейбниц біршама беріректе, XVII ғасырдың соңында құрды. Туынды туралы ғылымды жүйелі дамытып, олар анализдің екі проблемасын тұжырымдады:
1. Жүретін жолдың тұрақты (яғни кез келген уақыт мезетіндегі) ұзындығы берілген; көрсетілген уақыт ішіндегі қозғалыс жылдамдығын табу керек.
2. Қозғалыс жылдамдығы тұрақты берілген; көрсетілген уақыт ішінде жүрілген жолдың ұзындығын табу керек.
Бірінші ахуал дифференциалдық есептеудің даму бағдарламасына береді.
Ньютон механика есептерін негізге алса (ньютондық анализ ньютондық классикалық механикамен қатар жасалған-ды), Лейбництің артықшылығы ол геометрия есептерін негіз етіп алды.
Анализ идеяларының одан кейінгі дамулары туралы айтқанда (ол идеялар өте тез тарап кетті және өзіне көптеген ізбасарлар тапты) Лейбництің шәкірттері - ағайынды Я. Бернулли және И. Бернуллилердің есімдерін алдымен атаған жөн.
Негізі де, көрсеткіші функция болып келетін дәрежелік-көрсеткіштік функцияның туындысы Ньютонда да, Яков Берниллида да жоқ. Оны Лейбниц пен Иоганн Бернулли тағайындаған. Дифференциалдық есептемедегі анықталмаған өрнектерді шын мәндерін Иоганн Бернулли көрсеткен. Дифференциалдық теңдеулер теориясында

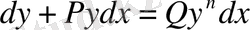
теңдеуі Бернулли теңдеуі деп аталады. Оны 1695 жылы Яков Бернилли ұсынған.
Иоганн Бернуллидың ғалымдарға жазған хаттарында да құнды мағлұматтар кездеседі. Оларда бір тектес дифференциалдық теңдеулердің ауыстырмасы арқылы айнымалылары айырылатын теңдеулерге келтірілетіндігі, осы күні Лагранж теңдеуі деп аталатын

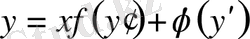
теңдеуінің шешілетіндігі, көптеген шектеусіз қатарлар айтылады.
А. Лопиталь (1661 - 1704) И. Бернуллиден дәріс алған, ол 1696 жылдың өзінде дифференциалдық есептеудің алғашқы курсы Қисық сызықтарды зерттеуге арналған шексіз аздар анализін баспадан шығарып үлгерді, бұл жаңа әдістердің таралуына септігін тигізді.
Бұл салада ірі нәтижелерге жеткен Лагранж еді, оның еңбектері анализ негіздерінің мән-мағынасын түсінуде зор роль атқарды. Лейбниц пен Ньютон қалдырған математикалық анализ Лагранжды қанағаттандырмаған, ол анализді қайта құруды көздеген. Анализдің ең негізгі ұғымдарының бірі - туынды ұғымы. Туынды ұғымы түсінікті түрде, айқын, тұжырымдалса, интеграл да, басқа ұғымдар да оңай тұжырымдалады. Туындыны штрих арқылы белгілеуші Лагранж болған
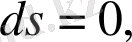
Туындылар таблицасы бойынша дифференциалдар таблицасын жасауға болады. Мысалы, 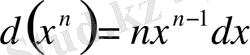т.с.с.
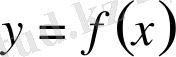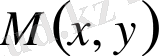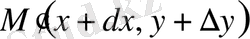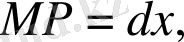
Дифференциалдың да геометриялық мағынасын (1 сурет) анықтауға болады. Координаталар системасына функциясының графигін салайық, оның бойынан және нүктелерін алайық. 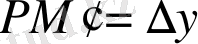болады. нүктесінен жанама жүргізсек, ол 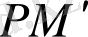түзуін бір нүктесінде қиып өтеді. Туындының геометриялық мағынасы бойынша 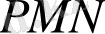бұрышының тангенсі 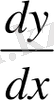туындыға тең. 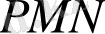үшбұрышынан 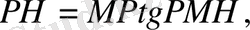яғни

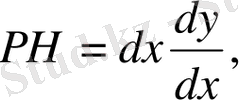
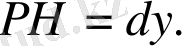
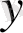M1 Н
M Р
y
0 x x=dx
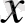
1 сурет

Сөйтіп, функцияның 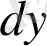дифференциалы жанау нүктесінің х абциссасы есептеудің өсімше қабылдағанда жанаманың оған сәйкес нүктесінің ординатасы қабылдайтын өсімше болып табылады. 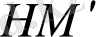кесіндісі функция өсімшесінің екінші бөлігі, яғни жоғары ретті шектеусіз шама болады. Сонымен, дифференциалдың геометриялық мағынасы - қисыққа жүргізілетін жанаманың бұрыштық коэффициенті.

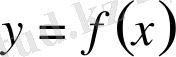функциясынын дифференциалданғанда 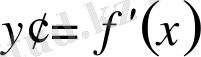туындысы шығады. Оны бірінші ретті туынды деп атайды. Бірінші ретті туындыны тағы да дифференциалдасақ, бірінші ретті туындының туындысын табамыз. Ол екінші ретті туынды деп аталып, екі штрих арқылы белгіленеді: .
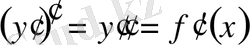Үшінші, төртінші т.с.с. ретті туындылар да бола береді. Үшінші ретті туынды. Төртінші, бесінші т.с.с.ретті туындыларда штрих орнына рим цифлары немесе жақшаға алынған үнді цифлары жазылады. Мәселен:
yVI - алтыншы ретті туынды,
y(38) - 38-нші ретті туынды,
yn - n-нші ретті туынды.
Бұлар кейде былай да белгіленеді:

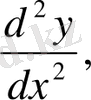
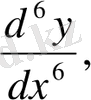
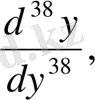
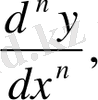
оқылуы "дэ екінші игрек бөлінген дэ икс квадрат" т.с.с.
Туындының ретін функцияның дәрежесімен шатастырмау керек. Олар екі түрлі ұғымға жатады.
Екінші, үшінші ретті т.с.с. ретті туындылар жоғары ретті туындылар деп аталады. Жалпы түрде:
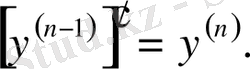
Мысал 1. 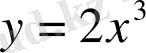-тің жоғары ретті туындыларын табыңыз.

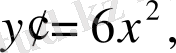
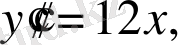
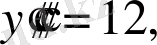
yIV=0.
Бұдан кейінгі туындылардың бәрі де нольге тең болады.
Екінші ретті туындының механикалық мағынасы бар: егер 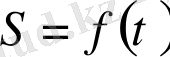функциясы қозғалыстың математикалық заңы болса, жолдың екінші ретті 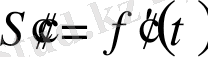туындысы үдеуді өрнектейді. Сондықтан үдеу жылдамдықтың туындысы болып табылады.

Мысал 2. 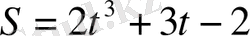, жол берілген. 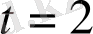болғанда үдеуді табыңыз.
Шешуі: 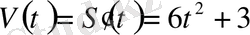-ке тең болады.
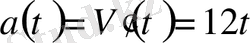болса, онда

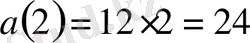
Жауабы:

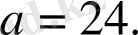
0.2 Туындыға қолданылатын теоремалар және туындының тәжірибеде қолданылуы

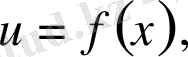
Есептер шығарғанда екі функцияның көбейтіндісінің n-ші ретті туындысын табуға тура келеді. 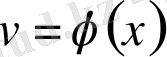болса,

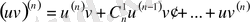
болады. Бұл теңдік Лейбниц формуласы деп аталады, ол көбінесе математикалық индукция әдісімен дәлелденеді. Формуладағы 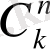коэффициенттері - Ньютон биномындағы терулер. Есте сақтау үшін бином жіктелуінің

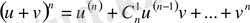
формуласын жазып, дәреже көрсеткіштерін туындының реті етіп, жақшаға алу керек және бірінші мүшеге 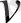ақырғы мүшеге қоса жазу керек.
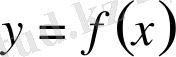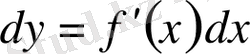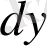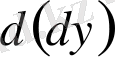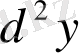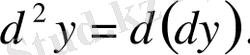
функциясының дифференциалы болатын мәлм. әдетте оны бірінші ретті дифференциал деп атайды. дифференциалын өзінен дифференциалын шығаруға болады. Бұл - екінші ретті дифференциал. Екінші ретті дифференциал деп белгіленеді, яғни: 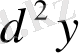өрнек дэ екі игрек деп оқылады. Сол сияқты: .
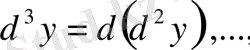
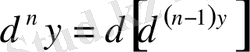Бұлар - екінші ретті дифференциалдар.
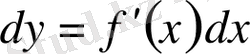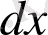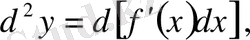
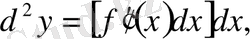
көбейтіндісін х бойынша дифференциалдағанда шама тұрақты көбейткіш ролінде болады, өйткені ол х-ке тәуелсіз. Сондықтан 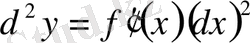болады. Жалпы түрде: 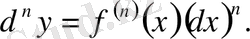Әдетте 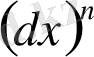орнына 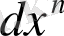деп жазады. Бұл арада n - дәреже көрсеткіш.
Графикте (2 сурет) функцияның ең үлкен мәнін кескіндейтін нүктенің көрші нүктелерінен жоғары (төбешікте) тұратыны, ал ең кіші мәнін кескіндейтін нүктенің көрші нүктелерінен төмен (шұқырда) тұратыны мәлім. Ондай нүктелерден өтетін жанамалар абсциссалар осіне параллель болады, яғни 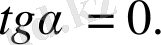сондықтан айтылып отырған нүктелерде туынды нольге тең болады. Туындының бұл қасиеті былай айтылады:
Егер 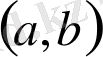интервалында үздіксіз 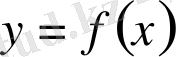функциясы осы интервалдың бір ішкі с нүктесінде өзінің ең үлкен немесе ең кіші мәнін қабылдайтын болса және функцияның с нүктесінде тиянақты туындысы болса, ол туынды нольге тең болады. (Ферма теоремасы).
y

0 a c1 c2 b
2 сурет
Егер дифференциалданатын функцияның графигі а мен b нүктелерінде абсциссалар осін қиып өтетін болса, осы аралықта оның ең кемінде бір жанамасы абсциссалар осіне параллель болады. Бұдан мынадай қорытынды шығады:
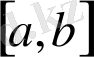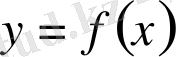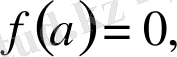
сегментінде дифференциалданатын функциясы сегменттің ұштарында нольге айналатын болса, (3 сурет) яғни 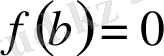болса, берілген функцияның туындысы сегменттің ішкі нүктелерінде ең кемінде бір рет нольге айналады (Ролль теоремасы).

a 0 b x
(3 сурет)
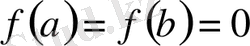болмай, 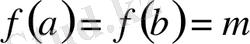болса да (- нольден өзгеше) теорема күшінде қалады. Мұны дәлелдеу үшін координаталар осьтерін параллель жылжытып, координаталар басын (0, ) нүктесіне көшіру керек.
Аса маңызды теоремалардың бірі - Коши теоремасы.
Ол былай тұжырымдалады:
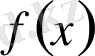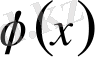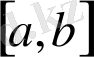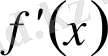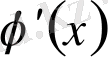Егер және функциялары сегментінде үздіксіз болса және сегменттің ішкі нүктелерінің бәрінде де олардың сәйкес және туындылары болса, 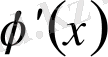туындысы сегменттің ішкі нүктелерінің ещқайсысында нольге айналмаса, 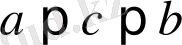теңсіздіктерін қанағаттандыратын с нүктесі табылады,
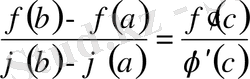теңдігі орындалады.
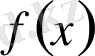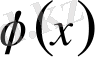Теореманы дәлелдеу үшін берілген және функциялары арқылы төмендегідей көмекші 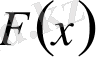функциясын құрастырамыз: .
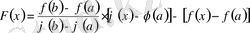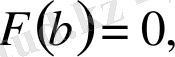
х орнына b мен а сандарын қойып есептесек, 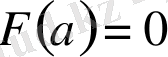болып шығады (көмекші функция әдейі, осылай болатындай етіліп алынған). Сондықтан 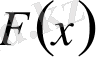функциясына Ролль теоремасын қолдануға болады. 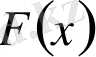функциясының туындысын табамыз:

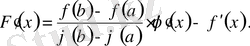
Ролль теоремасы бойынша 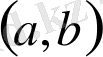интервалында бұл туындыны нольге айналдыратын ең кемінде бір с нүктесі болады, яғни 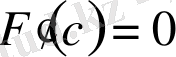. Сонда:
.
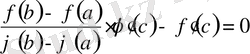Бұдан:

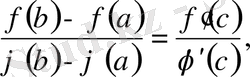
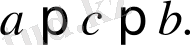
Теорема дәлелденді. Соңғы теңдік Коши формуласы деп аталады. Ол тәжірибеде жиі қолданылады.
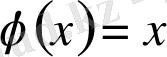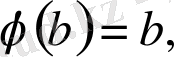
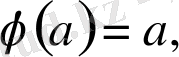
деп алсақ, 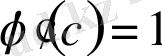болады да, Коши формуласы мына түрге келеді:

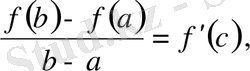
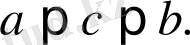
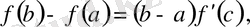
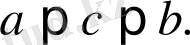
Бұл теңдік Лагранж формуласы деп аталады. Формуланың мазмұны төмендегідей:
Егер 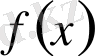функциясы 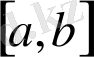сегментінде үздіксіз болса және сегменттің ішкі нүктелерінің бәрінде де оның 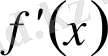туындысы болса, 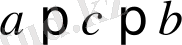теңсіздіктерін қанағаттандыратын бір с нүктесі табылады да, 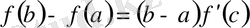теңдігі орындалады (Лагранж теоремасы).
Ағылшын математигі Брук Тейлор (1685 - 1731) мынадай формула қорытып шығарған:
.
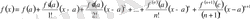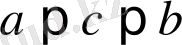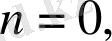
Мұнда , 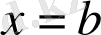болғанда Тейлор формуласы Лагранж формуласына айналады.
Тейлор формуласы математиканың көптеген салаларында қолданылады.
Берілген функцияны дифференциалдап, туындылары бойынша, оның экстремумы бар немесе жоқ екендігін, егер болса, қандай екендігін анықтауға болады. Ол жөнінде әр түрлі ережелер бар. Жиі қолданылатын ереже төмендегідей:
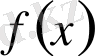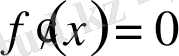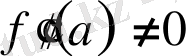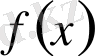нүктесінде функцияның бірінші ретті туындысы нольге тең, екінші ретті туындысы нольден өзгеше, яғни , болса, а нүктесінде функциясының экстремумы болады және екінші ретті туынды теріс сан болса, а нүктесіндегі экстремум максимум, оң сан болса, - минимум болады.
Мысал 4.

.
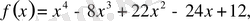
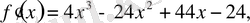
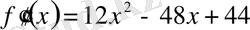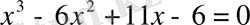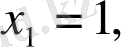
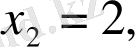
Бірінші ретті туындыны нольге тең етіп жазғанда теңдеуі шығады. Одан: 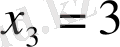. Функцияда экстремум болса, тек осы нүктелерде ғана болады, басқа нүктелерден іздеудің қажеті жоқ. х- тің табылған мәндерін қойып, екінші ретті туындының мәнін есептеп шығарам
.
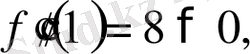
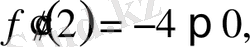
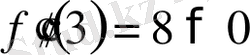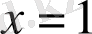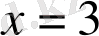Сонда ереже бойынша, және нүктелерінде минимум, 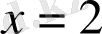нүктесінде максимум болады.
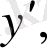
нүктесінде функцияның 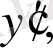..., 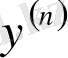туындыларының бәрі де нольге тең болып, 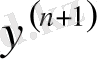туындысы нольден өзгеше болуы мүмкін. Мұндайда эксвтремум жөніндегі мәселе соңғы туынды бойынша шешіледі: нольден өзгеше 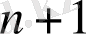- нші ретті туындыда 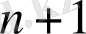тақ сан болса, яғни 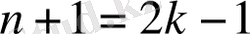болса, нүктесінде экстремум мүлде болмайды, ал 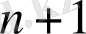жұп сан болса, яғни 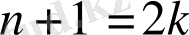болса, нүктесінде функцияның экстремумы болады және 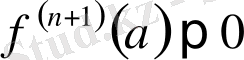болғанда максимум, 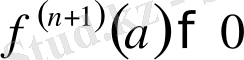болғанда минимум болады.
Бірнеше аргументі бар функциялардың да туындылары мен дифференциалдарын есептеп шығаруға болады. Мысалы, 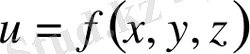функциясын х бойынша 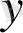бойыншы және 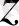бойынша жеке-жеке дифференциалдауға болады. Бұдан шығатын туындылар дербес туындылар деп аталады да,

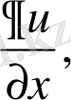
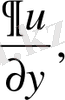
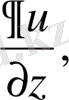
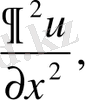
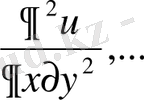
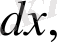
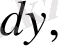
түрінде белгіленеді. 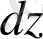тәуелсіз айнымалылардың дифференциалдары,

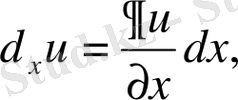
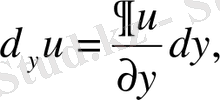
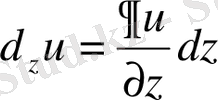
функцияның дербес дифференциалдары болады. Бұлардың қосындысы бірінші ретті толық дифференциал деп аталады. Ол 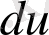деп белгіленеді.

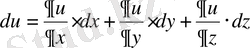
Мұндай функцияларды дифференциалдағанда да туындылардың жоғарыда келтірілген таблицасы қолданылады, тек х бойынша дифференциалдағанда 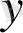пен 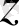-ті тұрақты ролінде алу керек, өйткені 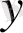пен 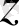-ке жөнінде де солай.
Мысал 5. 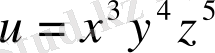болса,

, ,
,

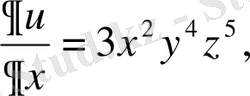
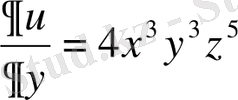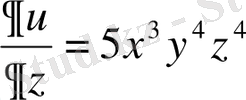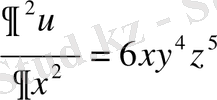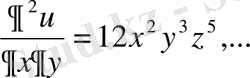
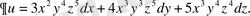
Туынды арқылы алгебралық және тригонометриялық теңдеулерді түрлендіруге, яғни өрнектерді көбейткіштерге жіктеуге болады.
Мысалдар қарастырайық.
Мысал 6. 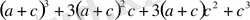өрнегін көбейткіштерге жіктеңіз.
Шешуі: с-ны айнымалы деп туындыны табамыз.
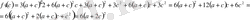
Онда ,

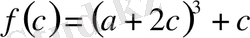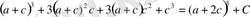
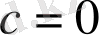деп алсақ 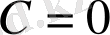, онда 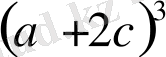өрнегі берілген функцияның шешімі болады.
Мысал 7. Теңсіздікті дәлелдеңдер: е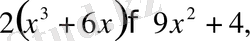гер егер
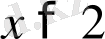
Дәлелдеуі: 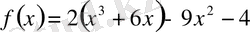функциясын қарастырайық та бұл функцияның 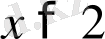жағдайда өспелі болатындығын көрсетейік.
Ол үшін функцияның туындысын тауып, оны түрлендірейік:
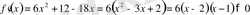себебі,
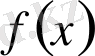функциясының туындысы оң болғандықтан, 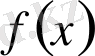өспелі функция болады да, қарастырылатын теңсіздік ақиқат болады.

2. Жаңартылған білім беру бағдарламасы бойынша туындыны қолдануды оқыту әдісі
2.1 Жаңартылған білім беру мазмұны аясында оқытудың негіздері

Орыс тілі ұлтаралық қарым-қатынас құралы ретінде және Қазақстан Республикасының ресми тілі ретінде жетекші ережелердің бірін алады. Қоғамда жұмыс істейтін қазақ-орыс қостілділігі қазақ мектебі оқушыларының орыс тілін меңгеру процесінде оң рөл атқарады. Тіл үйрену оқушыларға әлемдік деңгейдегі өзгерістерге бейімделуге, тілдік құндылықтарды түсінуге және айналасындағы өмірге жаңа көзқараспен қарауға көмектеседі.
Біз, екінші тіл мұғалімдері, бұл жағдайда қазақ тілінде оқытатын сыныптардағы орыс тілі, балаларға тілдерді үйренудің маңыздылығын үйретуіміз керек. Түсіну, орыс тілін құрметтеу, ху оқудан ләззат алу- көркем, ғылыми әдебиеттер мен БАҚ материалдары терең білім мен ойлау дағдыларын алуға, сондай-ақ сыни және шығармашылық білдіруге ықпал етеді.
Бүгінгі таңда сөйлеу мәдениеті айтарлықтай өзгерістерге ұшырайды. Олардың арасында біз бөлінсін мұндай оң үрдіс ретінде:
экономикалық, саяси және заң лексикасы саласында тілдің сөздік құрамын кеңейту;
БАҚ тілін шындықты сенімді жариялау қажеттіліктеріне жақындату.
Қазіргі сөйлеудегі осы оң тенденциялармен қатар теріс тенденциялар да дамыды:
көптеген негізсіз қарыздар;
сансыз инновациялар;
сөйлеу сәнін ұстану;
ауызекі сөздерді, жаргондарды, вульгаризмдерді, құнсызданған лексиканы шамадан тыс қолдану;
сленгтерді қолдану;
жалпы мәдениет деңгейінің төмендеуі және соның салдарынан сөйлеу мәдениеті.
Сондықтан біздің міндетіміз-ұлттық тілдік және мәдени дәстүрлерді сақтау. Оқушылар арасында қысқартылған стилистикалық бояу сөздерін қолдану едәуір өсті, бұл ана тілдерінің тілдік құзіреттілік деңгейінің төмендеуіне, жеке сөздіктің сарқылуына және әдеби тіл нормаларының бұзылуына әкеледі.
Әрине, біз қазіргі әлемде оқушының сөйлеу мәдениетін қалыптастырудың қайнар көзі тек мектеп қана емес, сонымен бірге отбасы, кітаптар, достар, БАҚ, ИНТЕРНЕТ, сонымен қатар теледидар мен ИНТЕРНЕТ-оқушылардың құндылық көзқарастарын, соның ішінде тілді қалыптастыруға белсенді әсер ететін ең жаппай және қол жетімді ақпарат құралы екенін жақсы түсінеміз. Демек, біз баланы дұрыс сөйлеуге және дұрыс сөздерді тілдік тұрғыдан дұрыс емес өрнектерден ажыратуға ғана емес, сонымен қатар контекст пен қарым-қатынас жағдайына қатысты тілдік құралдарды қолдануға үйретуден көреміз. Оқушылар білуі тиіс таңдау барлығы тіл байлығын бойынша қажетті мәні сөздер немесе нысандарын сақтау бірлігі стиль аулақ қайталау, қамқорлық таза және благозвучии сөйлеу. Мұны мұғалім үйретуі керек.
Мен орыс тілін бастауыш сыныптарда жаңартылған оқу бағдарламасы бойынша жүргіземін.
Қазақ сыныптарында "орыс тілі" пәнін оқытуда қолданылатын педагогикалық тәсілдер.
Мұғалімдердің алдында жаңа дилемма пайда болды: студенттер тәуелсіз, ынталы, қызығушылық танытатын, сенімді және интеллектуалды дамыған адамдар болуы керек.
Оқушыларға осы қасиеттерді қолдана отырып, тәрбиелеу және дамыту қажет:
- оқыту мен оқытудағы іс-әрекеттік тәсіл (оқу іс-әрекеті негізінде оқушылар жаңа білім алу қажеттілігін түсінуге келеді);
- зерттеу тәсілі (мен білгенімді білгім келетінін білемін);
- дамытушылық оқыту (оқушы іс-әрекет тәсілдерін меңгереді, өзінің оқу қызметін құрастыруды және оны басқаруды үйренеді);
- "оқу үшін бағалау" арқылы оқушыларды ынталандыру, оқытуды қолдау;
- оқушыларды өзара бағалау, өзара оқыту;
- оқушылардың жеке, топтық іс-әрекетін және бүкіл сынып жұмысын ұйымдастыру;
сараланған оқыту (қалыптастырушы бағалау арқылы оқушының қажеттіліктеріне сәйкес тапсырмалар қою).
Орыс тілі пәнін оқытудың ұсынылатын стратегиялары, әдістері мен технологиялары:
- стратегиялар: өзін-өзі басқару, эксперименттік, сыни, коммуникативті, контекстік;
- технологиялар: шағын топтарда (командада) жұмыс істеу, кейс-сатылар( нақты жағдайларды талдау), рөлдік және іскерлік ойындар, модульдік оқыту;
- әдістері: проблемалық оқыту, жеке оқыту, пәнаралық оқыту, тәжірибе негізінде оқыту, жобалау әдісі.
Табысты өлшеу және оқытудағы келесі қадамдарды анықтау үшін оқытудың нақты мақсаттары мен жетістік критерийлерін белгілеуге назар аудару қажет.
Осы жастағы балалар үшін сабақтарды жоспарлау кезінде: қызмет түрлерінің әртүрлілігі, нәтижеге бағытталған, бірлесіп құру, ынтымақтастық атмосферасын құратын оқыту, тәрбиелеу және дамыту технологиялары мен әдістерін қолдану міндетті болып табылады.
Бастауыш сыныптарда оқу нәтижелерін бағалау үшін қалыптастырушы бағалау қолданылады. Ол арқылы мұғалім оқу бағытының дұрыстығын тексереді, оқушылардың қосымша уәждемесін беру қажеттілігін анықтайды, оқушылардың оқу жетістіктерін бағалауды жүзеге асырады. Қалыптастырушы бағалаудың компоненттері:
* мұғаліммен білім алушылармен ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.